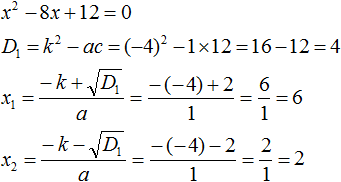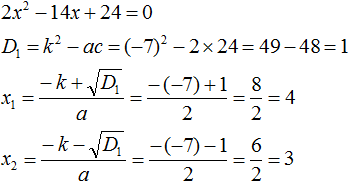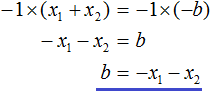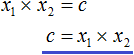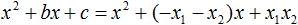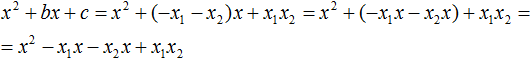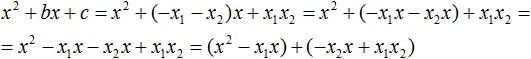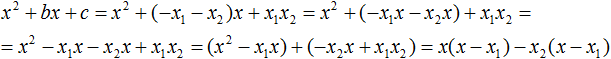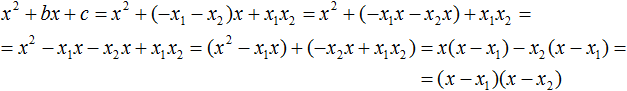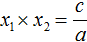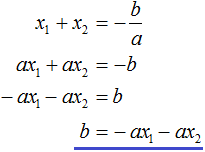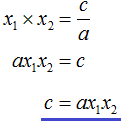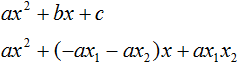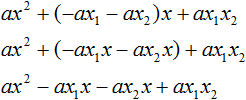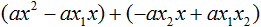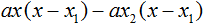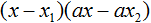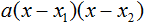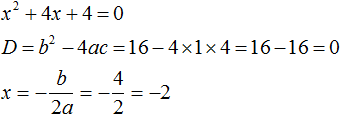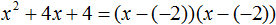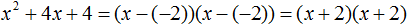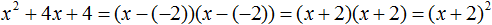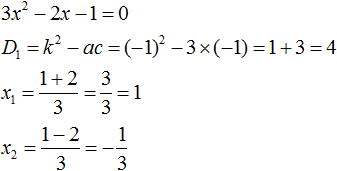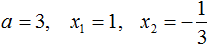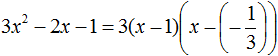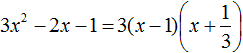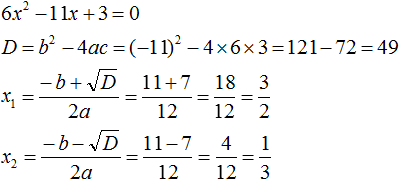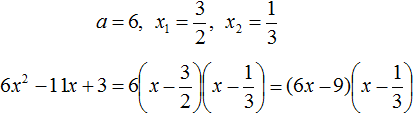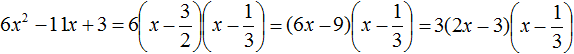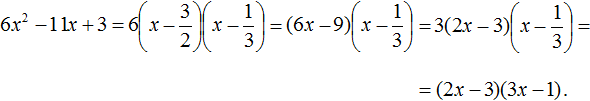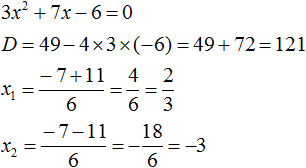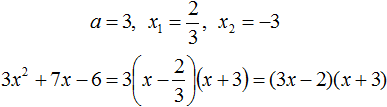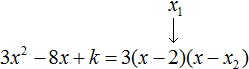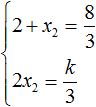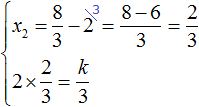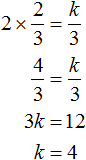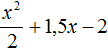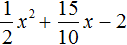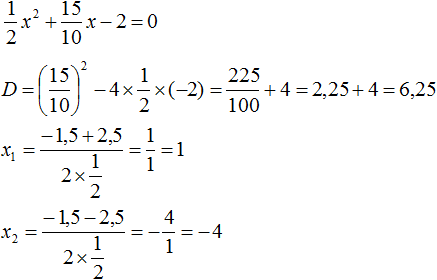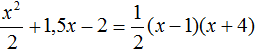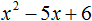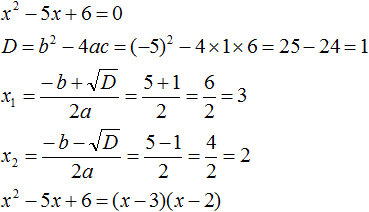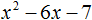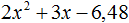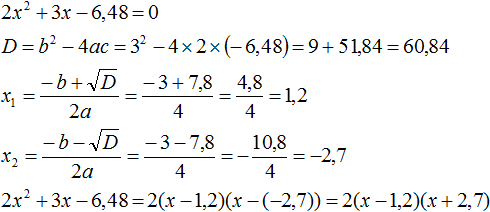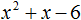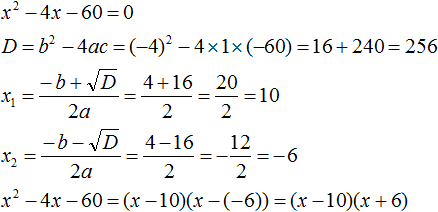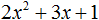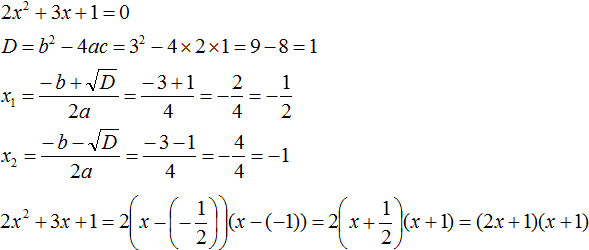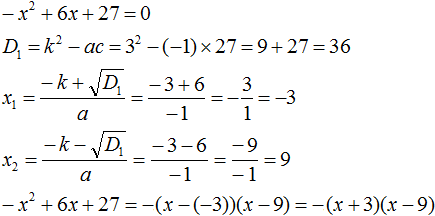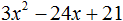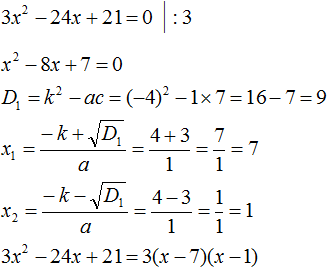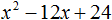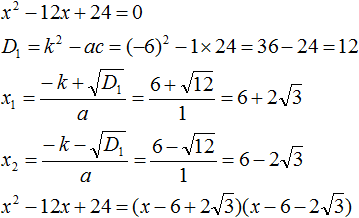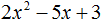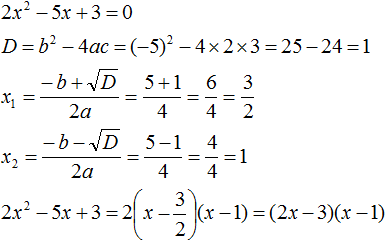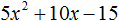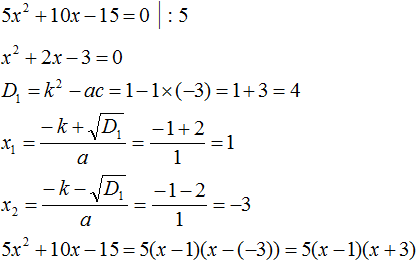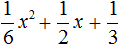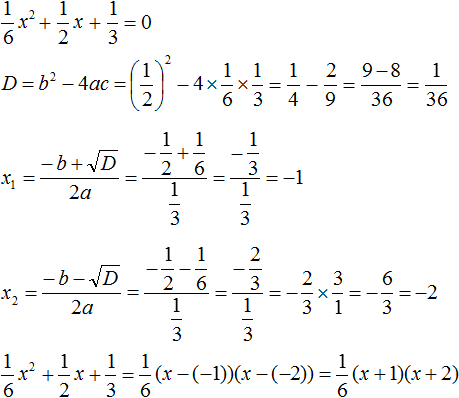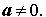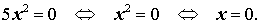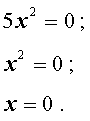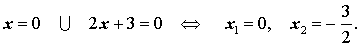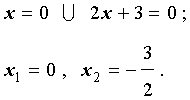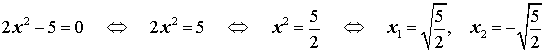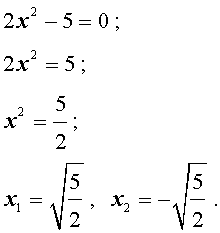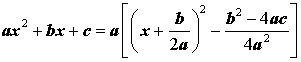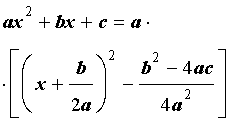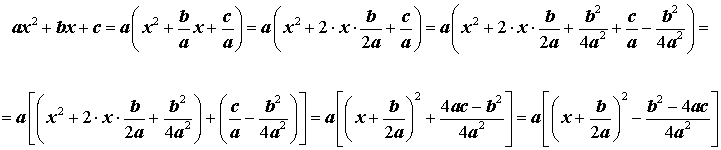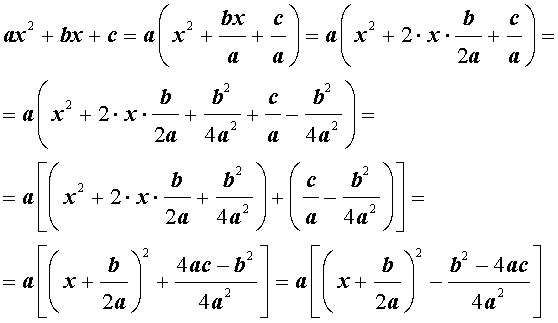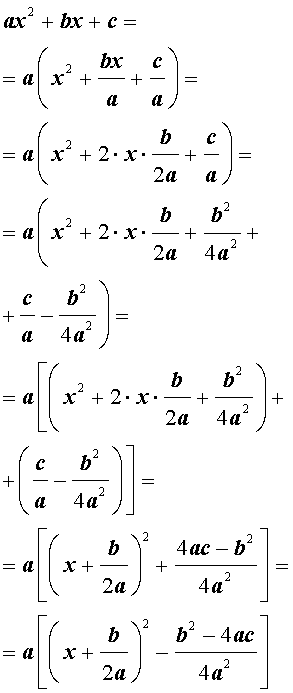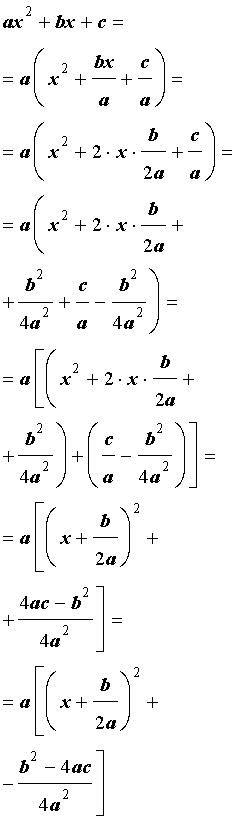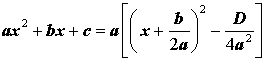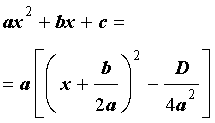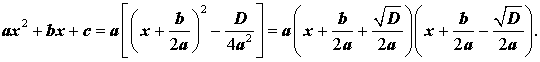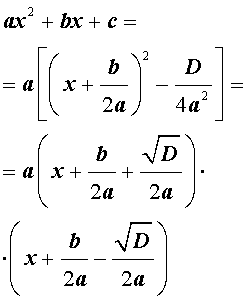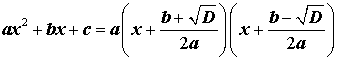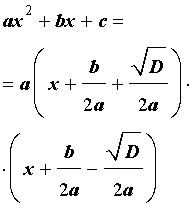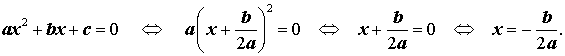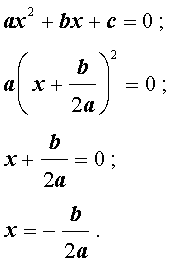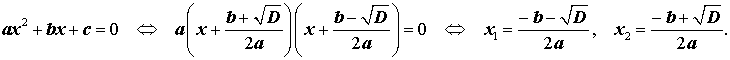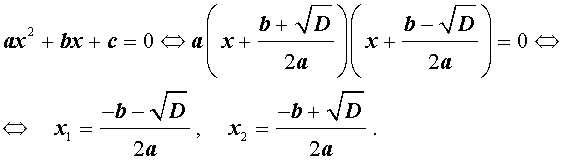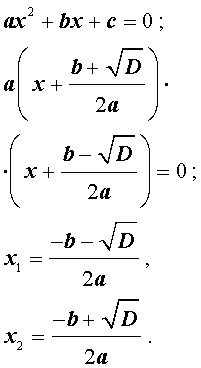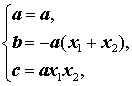- Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).
- Корень квадратного трехчлена:
- Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.
- Чтобы найти корни квадратного трехчлена нужно решить соответствующее квадратное уравнение.
- Разложение квадратного трёхчлена на множители:
- Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) — корни того же уравнения).
- Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.
- Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.
- Разложение квадратного трёхчлена на множители
- Как разложить на множители квадратный трёхчлен
- Как это работает
- Примеры разложений
- Задания для самостоятельного решения
- Квадратные уравнения
- Решение неполных квадратных уравнений
- Выделение полного квадрата
- Дискриминант
- Разложение квадратного трёхчлена на множители
- Формула для корней квадратного уравнения
- Прямая и обратная теоремы Виета
- 🎬 Видео
Квадратный трехчлен – это многочлен вида (ax^2+bx+c) ((a≠0)).
Почему его называют именно так? Потому что, наибольшая степень у него – квадрат, а состоит он из трех слагаемых ( одночленов ). Вот и получается – квадратный трехчлен.
Примеры не квадратных трехчленов:
(x^3-3x^2-5x+6) — кубический четырёхчлен
(2x+1) — линейный двучлен
Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Корень квадратного трехчлена:
Значение переменной (x), при котором квадратный трехчлен обращается в ноль, называют его корнем.
Пример:
У трехчлена (x^2-2x+1) корень (1), потому что (1^2-2·1+1=0)
У трехчлена (x^2+2x-3) корни (1) и (-3), потому что (1^2+2-3=0) и ((-3)^2-6-3=9-9=0)
Чтобы найти корни квадратного трехчлена нужно решить соответствующее квадратное уравнение.
Например: если нужно найти корни для квадратного трехчлена (x^2-2x+1), приравняем его к нулю и решим уравнение (x^2-2x+1=0).
Готово. Корень равен (1).
Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Разложение квадратного трёхчлена на множители:
Квадратный трехчлен (ax^2+bx+c) можно разложить как (a(x-x_1 )(x-x_2)), если дискриминант уравнения (ax^2+bx+c=0) больше нуля (x_1) и (x_2) — корни того же уравнения).
Например, рассмотрим трехчлен (3x^2+13x-10).
У квадратного уравнения (3x^2+13x-10=0) дискриминант равен 289 (больше нуля), а корни равны (-5) и (frac). Поэтому (3x^2+13x-10=3(x+5)(x-frac)). В верности этого утверждения легко убедится – если мы раскроем скобки , то получим исходный трехчлен.
Квадратный трехчлен (ax^2+bx+c) можно представить как (a(x-x_1)^2), если дискриминант уравнения (ax^2+bx+c=0) равен нулю.
Например, рассмотрим трехчлен (x^2+6x+9).
У квадратного уравнения (x^2+6x+9=0) дискриминант равен (0), а единственный корень равен (-3). Значит, (x^2+6x+9=(x+3)^2) (здесь коэффициент (a=1), поэтому перед скобкой не пишется – незачем). Обратите внимание, что тоже самое преобразование можно сделать и по формулам сокращенного умножения .
Квадратный трехчлен (ax^2+bx+c) не раскладывается на множители, если дискриминант уравнения (ax^2+bx+c=0) меньше нуля.
Например, у трехчленов (x^2+x+4) и (-5x^2+2x-1) – дискриминант меньше нуля. Поэтому разложить их на множители невозможно.
Пример. Разложите на множители (2x^2-11x+12).
Решение:
Найдем корни квадратного уравнения (2x^2-11x+12=0)
Полученный ответ, может быть, записать по-другому: ((2x-3)(x-4)).
Пример. (Задание из ОГЭ) Квадратный трехчлен разложен на множители (5x^2+33x+40=5(x++ 5)(x-a)). Найдите (a).
Решение:
(5x^2+33x+40=0)
(D=33^2-4 cdot 5 cdot 40=1089-800=289=17^2)
(x_1=frac=-5)
(x_2=frac=-1,6)
(5x^2+33x+40=5(x+5)(x+1,6))
Ответ: (-1,6)
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Разложение квадратного трёхчлена на множители
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как разложить на множители квадратный трёхчлен
Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Итак, x1 = 6 , x2 = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x1)(x − x2). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x1 = 6, x2 = 2
Если a равно единице (как в данном примере), то решение можно записать покороче:
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Итак, x1 = 4 , x2 = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x1)(x − x2) , где вместо переменных a , x1 и x2 подстáвим соответствующие значения. В данном случае a = 2
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24
Видео:Отрицательный дискриминантСкачать

Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x1 + x2 = −b . Для этого можно умножить обе его части на −1
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x2
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 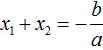
Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1
Теперь из второго равенства выразим c . Для этого умножим обе его части на a
Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:
Здесь вместо переменных b и c были подставлены выражения −ax1 − ax2 и ax1x2 , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax2
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:
Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x1)(x − x2) вместо переменных x1 и x2 .
Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x1 и x2 . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2
Тогда значение −2 в процессе разложения на множители будет подставлено вместо x1 и x2 . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x1)(x − x2) , где вместо a , x1 и x2 подстáвим соответствующие значения:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)
Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x1
Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби 
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Теперь из второго равенства выразим k . Так мы найдём его значение.
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим 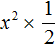
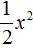
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Видео:Найти сумму корней квадратного уравнения, если дискриминант равен нулюСкачать

Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Видео:Решение квадратных неравенств графическим методом, если дискриминант равен нулю. 8 класс.Скачать

Квадратные уравнения
 Решение неполных квадратных уравнений Решение неполных квадратных уравнений |
 Выделение полного квадрата Выделение полного квадрата |
 Дискриминант Дискриминант |
 Разложение квадратного трехчлена на множители Разложение квадратного трехчлена на множители |
 Формула для корней квадратного уравнения Формула для корней квадратного уравнения |
 Прямая и обратная теоремы Виета Прямая и обратная теоремы Виета |
Квадратным трёхчленом относительно переменной x называют многочлен
| ax 2 + bx + c , | (1) |
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
| ax 2 + bx + c = 0, | (2) |
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
 | 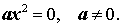 |
 | 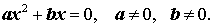 |
 | 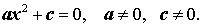 |
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
| 2x 2 + 3x= 0 . | (3) |
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
| x (2x+ 3) = 0 . | (4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ : 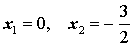
Пример 3 . Решить уравнение
Ответ : 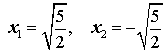
Пример 4 . Решить уравнение
| 3x 2 + 11 = 0 . | (5) |
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Ответ : 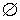
Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
| D = b 2 – 4ac. | (7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда 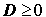
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
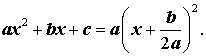 | (9) |
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
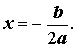 | (11) |
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
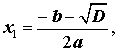 | (12) |
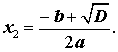 | (13) |
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
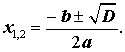 | (14) |
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
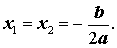 | (15) |
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . | (16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . | (17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Видео:Решение квадратных неравенств | МатематикаСкачать

Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
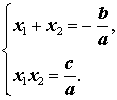 | (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
🎬 Видео
Как решать квадратные уравнения без дискриминантаСкачать

Быстрый способ решения квадратного уравненияСкачать

Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

ЛОВИ ПРОДОЛЖЕНИЕ 😉 ДИСКРИМИНАТ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать