В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.
- Определение уравнения плоскости
- Общее уравнение плоскости
- Нормальное уравнение плоскости
- Уравнение плоскости в отрезках
- Уравнение плоскости, виды уравнения плоскости.
- Уравнение плоскости – определение.
- Общее уравнение плоскости.
- Уравнение плоскости в отрезках.
- Нормальное уравнение плоскости.
- Различные виды уравнений плоскости в пространстве
- Различные виды уравнений плоскости в пространстве
- Примеры решения и задачи с методическими указаниями
- 🌟 Видео
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Определение уравнения плоскости
Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.
Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.
Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.
Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Общее уравнение плоскости
Сформулируем теорему, а затем запишем уравнение плоскости.
Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве
Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.
Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.
Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.
Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .
Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.
Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.
Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .
Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.
Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.
Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Нормальное уравнение плоскости
Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .
Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.
n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1
То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.
Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.
Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение плоскости в отрезках
Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.
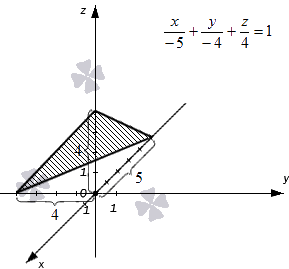
Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.
Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .
Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.
Видео:11. Прямая в пространстве и ее уравненияСкачать

Уравнение плоскости, виды уравнения плоскости.
В разделе плоскость в пространстве мы рассмотрели плоскость с позиций геометрии. В этой статье мы взглянем на плоскость с позиций алгебры, то есть, перейдем к описанию плоскости с помощью уравнения плоскости.
Сначала разберемся с вопросом: «Что такое уравнение плоскости»? После этого рассмотрим основные виды уравнения плоскости в прямоугольной системе координат Oxyz трехмерного плостранства.
Навигация по странице.
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение плоскости – определение.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и задана плоскость.
Плоскость, как и любая другая геометрическая фигура, состоит из точек. В прямоугольной системе координат Oxyz каждой точке соответствует упорядоченная тройка чисел – координаты точки. Между координатами каждой точки плоскости можно установить зависимость с помощью уравнения, которое называют уравнением плоскости.
Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x , y и z , которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.
Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.
Осталось выяснить, какой вид имеет уравнение плоскости. Ответ на этот вопрос содержится в следующем пункте этой статьи. Забегая вперед, отметим, что уравнение плоскости может быть записано по-разному. Существование различных видов уравнения плоскости обусловлено спецификой решаемых задач.
Видео:Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать

Общее уравнение плоскости.
Приведем формулировку теоремы, которая дает нам вид уравнения плоскости.
Всякое уравнение вида 

Уравнение 
Следует заметить, что уравнение вида 





Немного поясним смысл озвученной теоремы. В прямоугольной системе координат Oxyz каждой плоскости соответствует ее уравнение общего вида 

Если все коэффициенты А , В , С и D в общем уравнении плоскости 
Неполными уравнениями задаются плоскости, параллельные координатным осям, проходящие через координатные оси, параллельные координатным плоскостям, перпендикулярные координатным плоскостям, совпадающие с координатными плоскостями, а также плоскости, проходящие через начало координат.
Например, плоскость 

Отметим также, что коэффициенты A , B и C в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.
Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.
Рекомендуем ознакомиться с материалом статьи общее уравнение плоскости, где информация по теме изложена детальнее, подробно разобраны решения характерных примеров и задач.
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Уравнение плоскости в отрезках.
Уравнение плоскости вида 
Такое название не случайно. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox , Oy и Oz соответственно, считая от начала координат. Знак чисел a , b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.
Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках 

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках, там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Нормальное уравнение плоскости.
Общее уравнение плоскости вида 



Часто можно видеть, что нормальное уравнение плоскости записывают в виде 


Нормальное уравнение плоскости в прямоугольной системе координат Oxyz определяет плоскость, которая удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости 
Приведем пример нормального уравнения плоскости.
Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида 



Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости.
Рекомендуем более детально разобраться с данным видом уравнения плоскости, посмотреть подробные решения характерных примеров и задач, а также научиться приводить общее уравнение плоскости к нормальному виду. Это Вы можете сделать, обратившись к статье нормальное уравнение плоскости.
Видео:5. Нормальное уравнение плоскости выводСкачать

Различные виды уравнений плоскости в пространстве



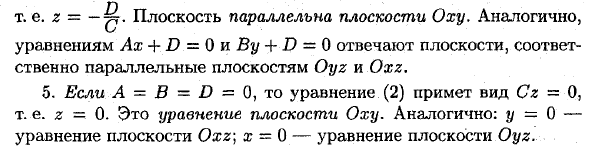


Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Различные виды уравнений плоскости в пространстве
- РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЙ ПЛОСКОСТИ В ПРОСТРАНСТВЕ Простейшая поверхность является плоскость. Плоскость в пространстве Oxijz можно задать разные способы. Каждая из них соответствует определенному виду ее уравнение. 1. Уравнение плоскости, проходящей через точку точки перпендикулярно существующего вектору Пусть в пространстве Oxyz плоскость Q задана точкой Mq <XQ уо; зо) и вектором п = (А ;. В С), перпендикулярным этой плоскости
Выведем уравнение плоскости Q. При любом расположении точки М на плоскости Q векторы п и ДМК взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: п • ДМК = 0, т е , А (х-®0) + В (у-у0) + С (z-z0) = 0. (1) Координаты любой точки плоскости Q удовлетворяют (1), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них п • Л / о М ф 0).
Уравнение (1) называется уравнением плоскости, проходящей через данную точку Mq (хо уо; ZQ) .перпендикулярно вектору п =. (Л; В; С) Оно первой степени относительно текущих координат ху у и г. Вектор п — (А В С) называется нормальным вектором плоскости. .. Придавая коэффициентам А, В и С уравнения (1) различные значения, можно получить уравнение любой плоскости, проходящей через точку Mq Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей а уравнение (1) — уравнением связки плоскостей.
Рассмотрим общее уравнение первой степени с тремя переменными х, у vi z: (2) Ax + By + Cz + D = 0. Не равны нулю, например, В и 0, пеме (3) Сравнивал уравнение (3) с уравнением (1), видим, что уравнения (2) и (3) являются уравнением плоскости с нормальным вектором п = (А; В) С), проходящей через точку М (0; — Q; 0 ). Итак, уравнение (2) определяет в системе координат Oxyz некоторую плоскость.
Видео:Уравнение плоскости. 11 класс.Скачать

Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Частные случаи общего уравнения плоскости: 1. Если D = 0, то оно принимает вид Ах -f К + Cz = 0. Этому уравнению удовлетворяет точка 0. (0; 0; 0) Следовательно, в этом случае плоскость проходит через начало координат. . 2. Если С = 0, то имеем уравнение Ах -f- К + D = 0. Нормальный вектор п = + C (z-0) = 0.
т. е. 2 = — ^ 4. Плоскость параллельна плоскости Оху. уравнениям Ax + D = 0nBy + D = 0 взаимодействующих плоскостей, соответственно параллельных плоскостям Oyz и Ox yz 5. Если А = В = D = 0, то уравнению (2) примет вид Cz-О, т. Е. Z-0. Плоскости Oyz.
. Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость Найдем уравнение плоскости Q, проходящей через три данные точки Ми (XI; ил] Zi), М2 (х2; 2 / 25z2) и М3 (х3-, у3]. гз), не лежащие на одной прямой.
Уравнение плоскости, проходящей через три данные точки Людмила Фирмаль
Возьмем на плоскость спутника точку М (х; у; z) и составим предлагаемую MiM = (x-xi y-yi z-
zi), М М2y =) М М2y =) уг — 2/1; 2: 3
21) Эти векторы лежат на плоскости Q, следовательно, они компланарны Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем М М • М М2 • М М $ = 0, т. х-хх у-т / 1 z- Zi Xl -XI У2- У z2-Zi Хг -Xl 2/3-й Zt-Zi (4) = 0 Уравнение (4) есть уравнение плоскости, проходящее через три данные точки. 4. Уравнение плоскости в отрезках
Уравнение плоскости в отрезках Пусть плоскость пересекается на осях Ох, Оу и Оз соответственно соответственно отрезки, Ъ и с, т. П. Проходис Подставляя координаты этих точек в уравнение (4), получаем Раскрыв определитель, у нас hex-abc + abz -f асу = 0, т. Е. Ящик -I- асу 4- abz = abc или — +! + — =! • (5) азбука Уравнение (5) называется уравнением плоскости в отрезках на осях.
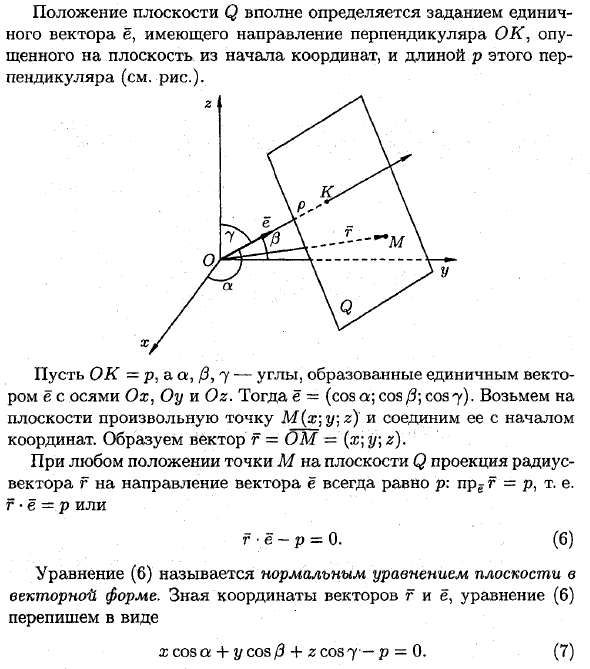
ПОЛОЖЕНИЕ В плоскости вполне определяется заданием единичного вектора ё, имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (см. Рис.). х
Пусть О К = р, а а, / 3,7 -. Углы, образованные единичный вектор с осями Ох, Оу и 02. Тогда ё = (потому что




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🌟 Видео
Видеоурок "Уравнение плоскости в отрезках"Скачать

Видеоурок "Общее уравнение плоскости"Скачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать

Видеоурок "Нормальное уравнение плоскости"Скачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение плоскости через 3 точкиСкачать