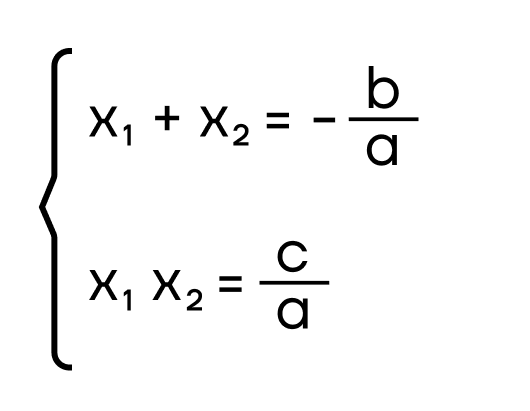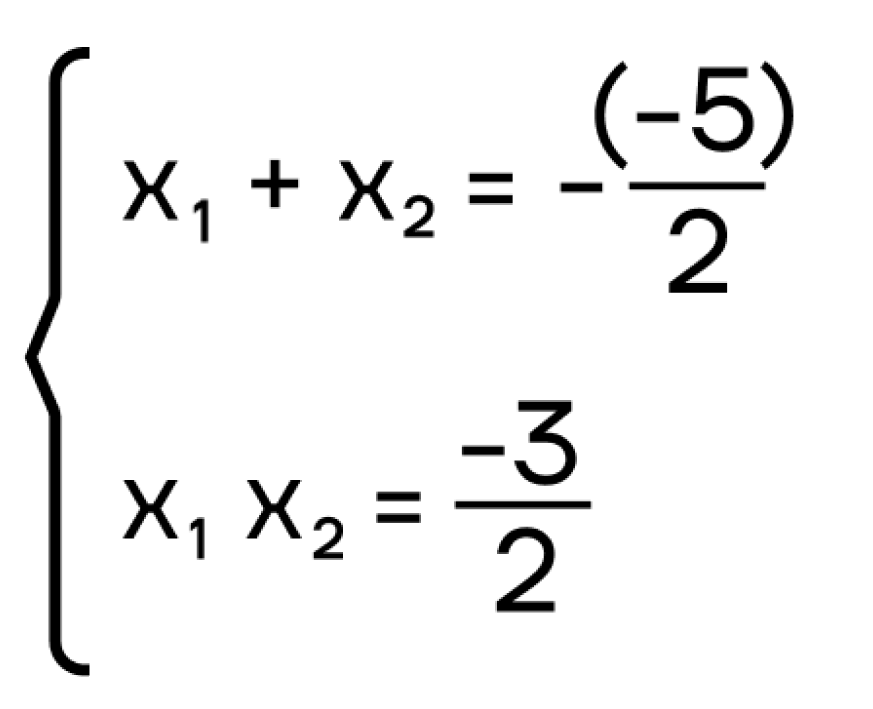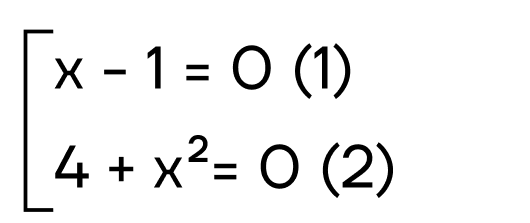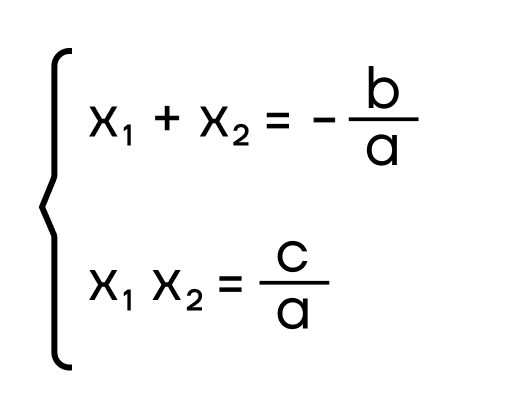Разделить обе части уравнения на одно и тоже число

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.
• Одночлены, из которых состоит многочлен, называют членами многочлена.
• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

• все решения уравнения являются координатами точек, принадлежащих графику;
• координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Видео:Как умножать или делить обе части уравнения на одно и тоже число.Скачать

2)Обе части уравнения разделили на одно и тоже число, отличное от нуля?

Математика | 5 — 9 классы

2)Обе части уравнения разделили на одно и тоже число, отличное от нуля.

Изменились ли корни данного уравнения?

3)сформулируйте правило переноса слагаемых из одной части уравнения в другую.

4)какие уравнения называют линейными?

2. не изменились

При переносе слагаемых из одной части уравнения в другую знак слагаемого изменяется на противоположный

Линейное уравнение— это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1.

Видео:Решение уравнений, 6 классСкачать

Какое равенство называют уравнением?

Какое равенство называют уравнением?

Какое число называют корнем уравнения?

Как найтти неизвестное слагаемое ; вычитаемое ; уменьшаемое?

Видео:Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать

Вставьте пропущенные слова так, чтобы получилось верное высказывание?

Вставьте пропущенные слова так, чтобы получилось верное высказывание.

А) Корни уравнения не изменяются, если обе части уравнения ______________ или_____________ на одно и тоже число, не равное ___________________.

Б) Корни уравнения не изменяются, если какое — нибудь слагаемое________________ из одной части в другую, ___________________ при этом знак.

Видео:Решение уравнений 3 урокСкачать

Какое из уравнений является линейным уравнением с одной переменной?

Какое из уравнений является линейным уравнением с одной переменной.

Видео:Теория. Умножение и деление обеих частей уравнения (5-8 класс)Скачать

Какое равенство называют уравнением?

Какое равенство называют уравнением?

Какое число называют корнем уравнения?

Что значить решить уравнение?

Как проверить, верно ли решено уравнение?

Как найти неизвестное слагаемое ; вычитаемое ; уменьшаемое.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Какое равенство называют уравнением?

Какое равенство называют уравнением?

Какое число называют корнем уравнения?

Видео:6 класс, 42 урок, Решение уравненийСкачать

CРОЧНО Решите уравнение : 16 х + 9 = 14х + 15 по алгоритму : 1) Перенести члены, содержащие переменную, в одну часть, а свободные члены — в другую?

CРОЧНО Решите уравнение : 16 х + 9 = 14х + 15 по алгоритму : 1) Перенести члены, содержащие переменную, в одну часть, а свободные члены — в другую.

2) Привести подобные слагаемые.

3) Обе части уравнения разделить на коэффициенты при х и найти корень уравнения.

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?

Как переносить дробь в другую часть уравнения и какие знаки становятся в числители, если он состоит не из одного числа а например 8 + 7, то плюс поменяется на минус?

Видео:Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

К * 7 = 574 преобразуй правую часть каждого уравнения так, чтобы решение уравнения потре бовало выполнения большего количества действий, но корни уравнений не изменились?

К * 7 = 574 преобразуй правую часть каждого уравнения так, чтобы решение уравнения потре бовало выполнения большего количества действий, но корни уравнений не изменились.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Решите уравнение 18x — 24 = 15x + 3 используйте описание ходаСоберём слагаемые с x в одной части уравнения, остальные в другойПриведём подобные членыРазделим обе части уравнения на коэффициент при x?

Решите уравнение 18x — 24 = 15x + 3 используйте описание хода

Соберём слагаемые с x в одной части уравнения, остальные в другой

Приведём подобные члены

Разделим обе части уравнения на коэффициент при x.

Видео:Линейное уравнение с одним неизвестным.Скачать

Упростите уравнение, разделив обе его части на одно и то же число, а затем найдите его корни : 9(7y — 5) — 3(9y + 11) = 6(15 — 4y) + 27?

Упростите уравнение, разделив обе его части на одно и то же число, а затем найдите его корни : 9(7y — 5) — 3(9y + 11) = 6(15 — 4y) + 27.

Перед вами страница с вопросом 2)Обе части уравнения разделили на одно и тоже число, отличное от нуля?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Линейные, квадратные и кубические уравнения

На этой странице вы узнаете:

• Почему неизвестное обозначают через x?
• Как находить корни квадратного уравнения, не считая их?
• Как дискриминант может повлиять на количество корней уравнения?

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Понятие уравнения

Главный секрет математики в том, что любую задачу можно решить уравнением. А решить уравнение – значит найти все его корни или доказать, что их нет.

Давай разберемся как это сделать.

Уравнение – это равенство, содержащее неизвестное, обозначенное буквой.

Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством.

Например, число 8 будет корнем уравнения 2x — 3 = 5 + x, потому что равенство 2 * 8 — 3 = 5 + 8 верное.

Видео:Уравнение вида ах = с 6 класс Часть 2 Теперь учимся высвобождать переменную от множителя.Скачать

Линейные уравнения

Что же такое линейное уравнение?

Линейное уравнение – это уравнение, в котором неизвестная находится в степени 1.

Вид линейного уравнения:

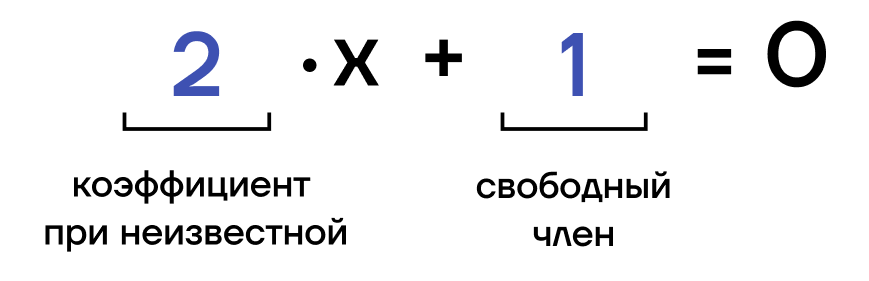
ax + b=0 , где
х – неизвестная
а – коэффициент при неизвестной
b – свободный член

Стоит отметить, что а и b в таком уравнение известны, также оба этих числа можно называть коэффициентами.

Как же решить такое уравнение?

Для решения линейного уравнения нужно выразить х и найти числовое значение, то есть сделать такие преобразования, чтобы в одной части уравнения осталась только неизвестная, а в другой собралось все остальное.

Преобразования, которые можно совершать:

1. Переносить слагаемое в другую часть уравнения с противоположным знаком.

x — 5 = 0
x = 0 + 5
x = 5

1. Умножать или делить обе части уравнение на одно и то же число или выражение, которое не равно нулю.

Давайте рассмотрим решение линейного уравнения на следующем примере

2(x + 5) — 4x + 2 = 0

1. Сначала раскроем скобки
   2x + 10 — 4x + 2 = 0

1. Для упрощения сложим подобные слагаемые
   -2x + 12 = 0

1. Теперь перенесем слагаемое без неизвестной в правую часть и разделим обе части уравнения на коэффициент при неизвестной, то есть выразим х
   -2x = -12 | : (-2)
   x = 6

Значение неизвестной найдено, а значит единственное решение данного уравнения 6

С линейными уравнениями можно столкнуться и в жизни.

Допустим, нам нужно приготовить 570 грамм теста на пирожки.

Обозначим вес одной части за x. Составим и решим уравнение для получения этого количества теста:

12x + 6x + x = 570
19x = 570
x = 30

Мы узнали, что одна часть — это 30 грамм. Теперь посчитаем сколько грамм продуктов нам потребуется.

• Мука: 12 * 30 = 360 грамм
• Вода: 6 * 30 = 180 грамм
• Растительное масло: 1 * 30 = 30 грамм

Видео:Равносильные уравненияСкачать

Квадратные уравнения

Мы уже знаем, что такое линейное уравнение. Но как же выглядит квадратное?

Квадратное уравнение – это уравнение, в котором неизвестная находится в степени 2.

Вид квадратного уравнения:

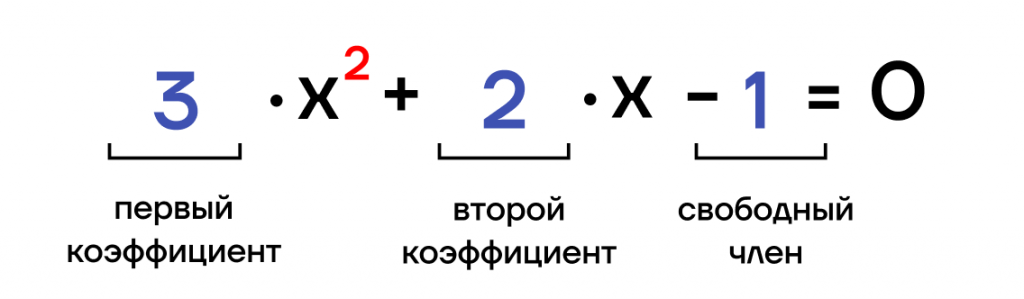
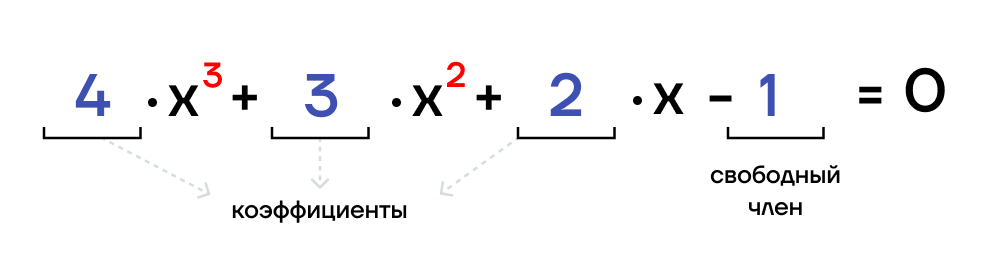
ax 2 + bx + c = 0 , где
х — неизвестная
а и b – коэффициенты при неизвестной
с – свободный член

Стоит отметить, что а, b и с – известные числа.

Какими бывают квадратные уравнения?

Эти виды квадратных уравнений отличаются тем, что у полного квадратного уравнения есть оба коэффициента и свободный член, а у неполного может отсутствовать или второй коэффициент, или свободный член.

Решение несколько неполных квадратных уравнений на примере:

x 2 + 2x = 0 x * (x + 2) = 0 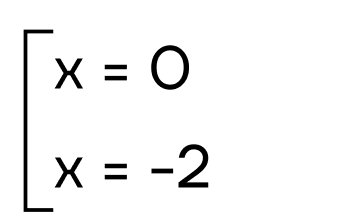Ответ: 0 и -2

x 2 — 4 = 0 x 2 = 4 x = ±2 Ответ: 2 и -2

Полное квадратное уравнение может иметь 2 корня, 1 корень или не иметь корней. Количество корней зависит от дискриминанта

Видео:Как решают уравнения в России и СШАСкачать

Что такое дискриминант?

Дискриминант в квадратном уравнении — это выражение, которое ищется по следующей формуле, где а, b и с берутся из уравнения:

D = b 2 — 4 ⋅ a ⋅ c

Как дискриминант может повлиять на количество корней уравнения? Если D > 0, то уравнение имеет 2 корня. Если D = 0, то уравнение имеет 1 корень. Если D Дискриминант нужен не только для определения количества корней, но и для их нахождения одним из способов. Способы решения квадратных уравнений: Решение через дискриминант Корни квадратного уравнения находятся по этим формулам, где а и b берутся из уравнения, а D – это дискриминант: По теореме Виета Как находить корни квадратного уравнения, не считая их? По теореме Виета корни нужно подбирать, поэтому она удобна для нахождения рациональных корней. Данная теорема заключается в связывании корней уравнения и коэффициентов многочлена системой двух уравнений. где а, b и с – коэффициенты квадратного уравнения x1 и x2 – корни квадратного уравнения Давайте рассмотрим решение квадратного уравнения на следующем примере 1 способ: D = (-5) 2 — 4 ⋅ 2 ⋅ (-3) = 25 + 24 = 49 Дискриминант больше нуля, следовательно, у уравнения 2 корня, найдем их Решениями уравнения являются числа 3 и -12. 2 способ: Запишем систему по теореме Виета Теперь подберем такие два числа, чтобы их сумма была (frac), а произведение -(frac), это будут числа 3 и -12. Значит, решениями уравнения являются числа 3 и -12. Видео:Решение уравнений - математика 6 классСкачать Кубические уравнения Перейдем к последнему виду уравнений. Что же такое кубическое уравнение и как оно выглядит? Кубическое уравнение – это уравнение, в котором неизвестная находится в степени 3. Вид кубического уравнения: ax 3 + bx 2 + cx + d = 0, где х — неизвестная а, b и с – коэффициенты при неизвестной d – свободный член Стоит отметить, что а, b, с и d – известные числа. Преобразования, которые можно совершать в кубических уравнениях: Вынесение общего множителя за скобки. Вынесение общего множителя за скобки можно сравнить с делением фруктов в обеих тарелках на одинаковые части и вынесением такой части в отдельную тарелку. Алгоритм: Разложить каждое слагаемое на множители. Вынести за скобку множители, которые есть в обоих слагаемых. Вынести скобку, как общий множитель. x 3 — 2x 2 — 3x = x * x * x — 2 * x * x — 3 * x = x * (x 2 — 2x — 3) Группировка Алгоритм: Объединить слагаемые в пары. Вынести общий множитель из каждой скобки, чтобы получились одинаковые скобки. 6x 3 + 9x 2 + 8x + 12 = (6x 3 + 9x 2 ) + (8x + 12) = 3x 2 * (2x + 3) + 4 * (2x + 3) = = (3x 2 +4) * (2x+3) Рассмотрим решение кубического уравнения 4x + x 3 = x 2 + 4 Перенесем все слагаемые в левую часть 4x + x 3 — x 2 — 4 = 0 Заметим, что удобнее группировать 1 и 2 слагаемые и 3 и 4 слагаемые (4x + x 3 ) — (x 2 + 4) = 0 Вынесем общий множитель х из первой скобки x * (4 + x 2 ) — (x 2 + 4) = 0 Вынесем ещё один общий множитель x 2 + 4 за скобки (x — 1) * (4 + x 2 ) = 0 Чтобы произведение было равно 0, один из множителей должен быть равен 0, запишем совокупность Решим каждое уравнение отдельно x — 1 = 0 x = 1 4 + x 2 = 0 x 2 = -4 Нет решений, так как x 2 ≥ 0 верно для любого х Из этого следует, что у данного уравнения есть только одно решение x=1 Видео:Математика 6 класс (Урок№50 - Уравнения. Часть 2.)Скачать Фактчек В линейном уравнении неизвестная находится в степени 1. Для решения такого уравнения в одной части уравнения нужно оставить только неизвестную, а в другой собрать все остальное. В кубическом уравнении неизвестная в квадрате, то есть в степени 2. Решать такое уравнение можно через дискриминант или по теореме Виета В кубическом уравнении неизвестная находится в кубе, то есть в степени 3. Для решения такого уравнения используется вынесение общего множителя за скобки и способ группировки. Видео:Решение уравненийСкачать Проверь себя Задание 1. Найдите корень уравнения (2x + 4) ⋅ 3 — 2x = 0 Задание 2. Сколько корней будет у уравнения x 2 + x — 2 = 0? Нет корней Один корень Два корня Три корня Задание 3. Найдите корни уравнения x 2 + 4x — 5 = 0 Задание 4. Найдите корни уравнения x 2 — 5x = 0 Задание 5. Найдите корни уравнения 12x + 4 — 12x 3 — 4x 2 =0 Ответы: 1. — 4; 2. — 3; 3. — 2; 4. -1; 5. — 3 📹 Видео Как решить уравнение #россия #сша #америка #уравненияСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства