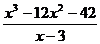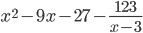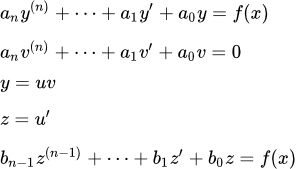Алгоритм деления в столбик применяется в частности при нахождении интегралов.
- Решение онлайн
- Видеоинструкция
Пример деления в столбик . Найти частное деления и остаток многочлена:
№1.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 |
| -9x 2 -42 |
№2.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 |
№3.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x -27 |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 | |
| -27x + 81 | |
| -123 |
Целая часть: x 2 -9x -27
Остаток: -123
Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.
Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1
Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)
- Решение задач по математике онлайн
- Калькулятор онлайн. Деление многочлена на многочлен (двучлен) столбиком (уголком)
- Немного теории.
- Деление многочлена на многочлен (двучлен) столбиком (уголком)
- Пример
- Решение дифференциальных уравнений высших порядков методом Бернулли
- Метод решения
- Пример 1
- Шаг 1. Вводим две функции
- Шаг 2. Решение однородного уравнения
- Шаг 3. Понижение порядка
- Шаг 4. Интегрирование
- Пример 2
- Шаг 1. Вводим две функции
- Шаг 2. Решение однородного уравнения
- Шаг 3. Понижение порядка
- Шаг 4. Решение дифференциального уравнения первого порядка
- 🎥 Видео
Видео:7 класс, 30 урок, Разложение многочленов на множители с помощью формул сокращённого умноженияСкачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена
Видео:РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

Немного теории.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Деление многочлена на многочлен (двучлен) столбиком (уголком)
В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).
Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов ( f(x) ) и ( g(x) ), ( g(x) neq 0 ), существуют единственные полиномы ( q(x) ) и ( r(x) ), такие что
$$ frac = q(x)+frac $$
причем ( r(x) ) имеет более низкую степень, чем ( g(x) ).
Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного ( q(x) ) и остатка ( r(x) ) для заданных делимого ( f(x) ) и ненулевого делителя ( g(x) )
Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Пример
Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ frac $$
Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой ( (x^3/x = x^2) )
|
|
2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого ( (x^2 cdot (x-3) = x^3-3x^2) )
|
|
3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой ( (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) )
|
|
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
|
|
5. Повторяем шаг 4.
|
|
6. Конец алгоритма.
Таким образом, многочлен ( q(x)=x^2-9x-27 ) — частное деления многочленов, а ( r(x)=-123 ) — остаток от деления многочленов.
Результат деления многочленов можно записать в виде двух равенств:
( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 )
или
$$ frac = x^2-9x-27 + frac $$
Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Решение дифференциальных уравнений высших порядков методом Бернулли
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Метод решения
Ранее мы рассмотрели метод Бернулли для решения линейных неоднородных дифференциальных уравнений первого порядка. Этот метод также можно применить и для решения уравнений высших порядков. Если нам известно частное решение однородного уравнения, то применяя метод Бернулли, мы можем понизить порядок уравнения.
Пусть мы имеем линейное неоднородное дифференциальное уравнение произвольного, n-го порядка:
(1) .
Здесь является функцией от независимой переменной x . Коэффициенты также являются функциями от x .
Метод Бернулли заключается в том, что мы ищем решение уравнения (1) в виде произведения двух функций:
(2) .
Здесь и – функции от переменной x .
Если в качестве взять частное (любое, отличное от нуля) решение однородного уравнения
(3) ,
то такая подстановка приводит к понижению порядка исходного уравнения (1).
Покажем это. Пусть нам известна функция , удовлетворяющая уравнению (3). Применим формулу Лейбница для n-й производной произведения двух функций:
.
Здесь – биномиальные коэффициенты.
Разобьем сумму на две части:
.
Тогда первая часть содержит только производные от неизвестной функции u . Подставим в (1) и сгруппируем члены:
.
В силу (3), сумма членов в скобках равна нулю. В результате получаем:
.
Это линейное неоднородное дифференциальное уравнение n-го порядка относительно неизвестной функции . Оно содержит производные функции u и не содержит саму функцию в явном виде. Выполнив подстановку , мы получим линейное неоднородное уравнение n-1 -го порядка.
См. «Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде».
Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Пример 1
Решить дифференциальное уравнение с постоянными коэффициентами второго порядка методом Бернулли (введением двух функций):
(П1.1)
Шаг 1. Вводим две функции
Ищем решение в виде произведения двух функций:
(П1.2) .
Подставляем в уравнение (П1.1) и группируем члены:
;
(П1.3) .
Шаг 2. Решение однородного уравнения
Решаем однородное уравнение
(П1.4) .
Ищем решение в виде . Получаем характеристическое уравнение:
.
Решаем квадратное уравнение:
.
Получаем кратные корни: . Этим корням соответствуют два линейно-независимых решения линейного однородного уравнения (П1.4):
.
В качестве функции мы можем взять любое решение уравнения (П1.4). Возьмем наиболее простое. Пусть
(П1.5) .
Шаг 3. Понижение порядка
Шаг 4. Интегрирование
Видео:ЕГЭ по математике. Деление многочлена на двучленСкачать

Пример 2
Решить дифференциальное уравнение второго порядка методом Бернулли:
(П2.1)
Шаг 1. Вводим две функции
Ищем решение в виде произведения двух функций:
(П2.2) .
Подставляем в уравнение (П2.1) и группируем члены:
;
(П2.3) .
Шаг 2. Решение однородного уравнения
Решаем однородное уравнение
(П2.4) .
Ищем решение в виде . Получаем характеристическое уравнение:
.
Оно имеет комплексные корни:
.
Этим корням соответствуют два линейно-независимых решения однородного уравнения (П2.4):
.
В качестве функции , мы можем взять любое, отличное от нуля, решение уравнения (П2.4). Возьмем
(П2.5) .
Шаг 3. Понижение порядка
Подставляем (П2.5) в (П2.3), учитывая (П2.4):
;
;
.
Мы получили дифференциальное уравнение, не содержащее функцию в явном виде. Сделаем подстановку . В результате получаем линейное дифференциальное уравнение первого порядка:
(П2.6) .
Шаг 4. Решение дифференциального уравнения первого порядка
Уравнение (П2.6) можно также решить методом Бернулли, но это проще сделать с помощью интегрирующего множителя. Умножим уравнение (П2.6) на и выполняем преобразования:
;
;
.
Интегрируем:
.
Возвращаемся к переменной u :
.
Интегрируем еще раз и вычисляем интегралы (см. «Интегрирование тригонометрических рациональных функций» и «Таблица неопределенных интегралов»):
;
;
;
.
Автор: Олег Одинцов . Опубликовано: 03-12-2017
🎥 Видео
Математика - Разложение трехчлена на множителиСкачать

001-015 Особенности линейной и квадратичной функцийСкачать

Схема Горнера. 10 класс.Скачать

Формула Тейлора за 3 минуты - bezbotvyСкачать

Разложить на множители: a^3+3a^2 b+3ab^2+28b^3Скачать

Математика без Ху!ни. Деление многочлена на многочлен.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Разложение многочлена на множители способом группировки. Алгебра, 7 классСкачать

Деление многочлена на многочленСкачать

11.1 Разложение элементарных функций в ряд Маклорена (часть1)Скачать

Разложение кубических выражений на множителиСкачать