| Название | Основные законы равновесия жидкость пар бинарных систем |
| Анкор | Раева_Фролкова_Н_2013_end.doc |
| Дата | 05.03.2018 |
| Размер | 1.12 Mb. |
| Формат файла |  |
| Имя файла | Раева_Фролкова_Н_2013_end.doc |
| Тип | Учебное пособие #16259 |
| страница | 1 из 3 |
| Подборка по базе: Т-1 Основные требования законодательства Российской Федерации об, Диплом Структура расходов (затрат) на производство и реализацию , Устройство и основные элементы конструкции машины постоянного то, Задачи Основные макроэкономические показатели.docx, Лекция Законы распределения.doc, ✔ 5. Основные положения по ремонту автомобилей.doc, Возникновение науки и основные этапы ее развития.doc, Лекция 2 Основные этапы становления и развития политической наук, 1. Основные инструменты для создания исполнения и управления инф, Лекция 1. Метрология — основные термины и определения.docx Министерство образования и науки Российской Федерации химических технологий имени М. В. Ломоносова Кафедра химии и технологии основного органического синтеза Раева В.М., Фролкова А.В. ОСНОВНЫЕ ЗАКОНЫ РАВНОВЕСИЯ ЖИДКОСТЬ – ПАР БИНАРНЫХ СИСТЕМ комиссией МИТХТ им. М.В. Ломоносова в качестве учебного пособия для студентов, проходящих обучение по направлению 240100 « Х имическая технология », дисциплина «Теория химико-технологических процессов органического синтеза» ББК 24.5 План 2013 г. (поз. № 156/13). Раева В.М., Фролкова А.В. Основные законы равновесия жидкость – пар бинарных систем. Учебное пособие. М.: МИТХТ. им. М.В. Ломоносова, 2013. — 40 с. Рассмотрены основные законы фазового равновесия жидкость – пар бинарных систем. Для студентов, проходящих обучение по направлению 240100 « Х имическая технология », дисциплина «Теория химико-технологических процессов органического синтеза». Раева В.М., Фролкова А.В., 2013 | Введение | 4 |
| 1. | Фазовые равновесия бинарных систем | 5 |
| 1.1. | Основные понятия | 5 |
| 1.2. | Характеристики бинарных систем | 9 |
| 2. | Фазовое равновесие жидкость – пар бинарных систем | 17 |
| 2.1 | Основное уравнение фазового равновесия бинарных двухфазных систем | 17 |
| 2.2. | Законы Коновалова | 20 |
| 2.3. | Законы Вревского | 27 |
| 3. | Эволюция бинарных азеотропов | 34 |
| Условные обозначения и сокращения | 37 | |
| Литература | 39 |
- , , . Перегонка жидкостей, ректификация. Учебное пособие (стр. 1 )
- СОДЕРЖАНИЕ
- 1.1. Равновесие в системе пар – жикость……………………………….8
- 1.2. Диаграмма t-x-y бинарной смеси………………………………….10
- 1.3. Сущность разделения жидких смесей ректификацией…………..11
- 1.4. Установка для непрерывной ректификации бинарной смеси…. 13
- 2.1. Насадочные колонны………………………………………………16
- 2.2. Тарельчатые колонные аппараты………………………………….24
- 31.1. Исходные данные к расчету……………………………………….32
- 3.2. Перечень допускаемых допущений……………………………….32
- 3.3. Материальный баланс……………………………………………. 33
- 3.4. Построение фазовых диаграмм…………………………………. 33
- 3.5. Определение рабочего флегмового числа………………………..33
- 3.6. Определение теоретического числа тарелок по методу Мак-Кеба и Тиле………………………………………………………………………37
- 3.7. Определение числа единиц переноса……………………………..38
- 3.8. Определение действительного числа тарелок……………………39
- ВВЕДЕНИЕ
- 1. ОСНОВЫ ТЕОРИИ ПРОЦЕССА РЕКТИФИКАЦИИ
- 1.1 Равновесие в системе пар-жидкость
- Фазовое равновесие
ВВЕДЕНИЕ
Первым этапом при разработке принципиальных технологических схем разделения многокомпонентных смесей в технологиях органических веществ является анализ физикохимических особенностей поведения систем, в том числе и при варьировании внешних условий (температура, давление). При наличии ограничений термодинамического характера на возможность разделения смесей на практически чистые компоненты или фракции заданного состава применяют специальные методы ректификации, ориентированные на принцип перераспределения полей концентраций между областями разделения.
Основным массообменным процессом в непрерывных крупнотоннажных производствах основного органического и нефтехимического синтеза является ректификация. Движущая сила данного процесса различие равновесных составов паровой и жидкой фаз. Ректификационное разделение определяется спецификой парожидкостного равновесия, законы которого для бинарных систем рассмотрены в данном пособии.
Уравнение Ван-де-Вааальса – Сторонкина является развернутой формой выражения условий равновесия между фазами. На его основе можно получить законы Коновалова и Вревского, определяющие характер изменения составов фаз гетерогенных равновесных систем при варьировании составов фаз и условий.
В учебном пособии рассмотрены бинарные системы. Для них возможно наглядное представление фазовых диаграмм, известна математическая моделью фазового равновесия, имеются массивы экспериментальных данных для анализа и сравнения поведения систем различных классов и при различных условиях, достаточно проста Экспериментальные данные бинарных систем непосредственно используются для моделирования фазовых равновесий многокомпонентных систем. Для расчетов процесса ректификации используются фазовые равновесия жидкость-пар и жидкость-жидкость-пар.
1. Фазовые равновесия бинарных систем
1.1. Основные понятия
Фазовое равновесие – это сосуществование термодинамически равновесных фаз гетерогенной системы , которое определяется равенством температуры всех частей системы (термическое равновесие ), равенством давления во всем объеме системы (механическое равновесие ) и равенством химических потенциалов компонентов (химическое равновесие) во всех фазах системы, что обеспечивает равновесное распределение компонентов между фазами:

Компоненты – химически индивидуальные вещества, из которых состоит термодинамическая система. В однокомпонентных системах фазы представлены разными агрегатными состояниями вещества. В многокомпонентных системах фазы имеют различный состав и свойства, агрегатное состояние фаз может быть различным или одинаковым.
Термодинамическая фаза – однородная по термодинамическим свойствам часть системы, отделенная от других фаз поверхностями раздела, на которых при фазовых переходах скачкообразно меняются некоторые экстенсивные свойства системы. Фаза является гомогенной частью гетерогенной системы.
Число степеней свободы системы, находящейся в состоянии термодинамического равновесия, определяется правилом фаз Гиббса:

Фазовые диаграммы графически отображают состояния равновесной системы в пространстве термодинамических переменных, например: температуры, давления и состава. Число фаз в бинарных системах может быть различно.
Состояние двухфазной бинарной системы жидкость пар (
Фазовые равновесия жидкость – жидкость и жидкость – твердое тело экспериментально исследуют при постоянном давлении, в качестве независимых переменных выступают состав и температура (рис. 2). Состояние трехфаз-
ной бинарной системы жидкость жидкость – пар в области расслаивания (

На рис. 2 представлены наиболее распространенные примеры фазовых диаграмм жидкость – твердая фаза и жидкость – жидкость – пар. Их полные множества включают большее число типов. На рис. 3 приведены более сложные диаграммы бинарных расслаивающихся систем. Здесь x‘ , x» – составы равновесных жидких фаз.
Диапазоны условий, в которых изучают фазовые равновесия, ограничены критическими точками. Это предельные точки на кривых равновесия фаз, в окрестностях которых фазовое равновесие нарушается, происходит потеря термодинамической устойчивости и фазы становятся неразличимыми.
Условие устойчивости фазы приведено ниже:

Критическая точка фазового равновесии жидкость – пар является конечной точкой на кривой испарения и характеризуется критическими значениями температуры Тс, давления Рс и объема Vc. Фазовый переход твердая фаза – жидкость характеризуется критической температурой плавления. Парожидкостное равновесие существует в диапазоне условий (Р, Т), ограниченном этими критическими точками.
На рис. 4 приведены диаграммы фазового равновесия жидкость – жидкость. Линии, соединяющие составы равновесных фаз (x‘ , x»), называются нодами жидкость-жидкость. Бинодаль – линия составов равновесных жидких фаз, отделяющая расслаивающуюся часть диаграммы от гомогенной (рис. 4).
В большинстве бинарных систем взаимная растворимость компонентов увеличивается при повышении температуры (рис. 4а). В верхней критической точке растворимости (ВКТР) жидкие фазы становятся неразличимыми, при дальнейшем повышении Т смесь является гомогенной.
В системах с нижней критической точкой растворимости (НКТР) увеличение температуры приводит к уменьшению взаимной растворимости (рис. 4б). Смеси с двумя критическими точками растворимости встречаются значительно реже (рис. 4в).
Данные фазовых равновесий жидкость – пар (гомогенная жидкая фаза) и жидкость – жидкость – пар (ограниченная взаимная растворимость компонентов) используются для расчетов ректификации бинарных смесей. Диаграммы
Диаграммы жидкость – жидкость необходимы при разработке экстрак
жидкость – жидкость необходимы при разработке экстракционного разделения и комплексов, сочетающих ректификацию и расслаивание жидкой фазы. Диаграммы жидкость – твердая фаза необходимы при разработке комплексов разделения бинарных смесей, сочетающих ректификацию и кристаллизацию.
1.2. Характеристики бинарных систем
Бинарные жидкие растворы могут быть классифицированы по характеру и интенсивности межмолекулярных взаимодействий (ММВ) между компонентами в фазах и отклонениям фаз от идеального поведения, по избыточным термодинамическим функциям, а также по наличию или отсутствию расслаивания жидкой фазы (гомогенные и гетерогенные смеси) и др.
Степень неидеальности жидкой фазы определяется ММВ в растворе. Принято считать, что при одинаковой интенсивности ММВ между одноименными и разноименными молекулами 


Бинарные неидеальные растворы характеризуются различными отклонениями от идеального поведения, которые находят отражение в избыточных термодинамических функциях.
Функциями смешения ф М в термодинамике называют разности между значениями термодинамических функций в образованном растворе (ф р ) и аддитивными значениями, определяемыми из величин для чистых компонентов при постоянных давлении и температуре:

Избыточные термодинамические функции – разность между функциями смешения реального и идеального растворов:

Идеальные растворы характеризуются нулевыми значениями всех избыточных термодинамических функций: 

На рис. 5 приведены примеры концентрационных зависимостей избыточных функций бинарных гомогенных растворов, связанных при P=const и T=const термодинамическим соотношением:

Данные состав – избыточное термодинамическое свойство для бинарных растворов регулярно публикуются в специальной и справочной литературе. В подавляющем большинстве случаев они приводятся для атмосферного давления.
Компоненты с ограниченной взаимной растворимостью образуют расслаивающиеся смеси (рис. 6). Условие появления критической точки (7) означает, что в области расслаивания 


Рис. 5. Примеры концентрационных зависимостей избыточных
термодинамических функций бинарных гомогенных растворов.
Условие (7) может быть выражено в терминах избыточных энтальпии и энтропии для верхней критической точки растворимости (рис. 4а, 6а, б) в виде:


В области расслаивания избыточная энтропия может принимать как положительные, так и отрицательные значения, а величина избыточной энтальпии в таких системах должна быть строго положительной.
При реализации НКТР (рис. 4б, 6в) выполняются следующие условия:


Знаки обеих избыточных функций здесь строго отрицательны. Системы с двумя критическими точками растворимости (рис. 4в) характеризуются знакопеременными концентрационными зависимостями избыточной энтальпии (рис. 6г).
Смеси идеальных газов представляют собой идеальные газовые растворы. Поведение реальных газов описывают различными уравнениями состояния, в которых характер и степень отклонения от идеального поведения учитываются коэффициентами 

Здесь Vi 0п – объем реального газа (паровой фазы), V ид – объем идеального газа.
В условиях фазового равновесия жидкость – пар одновременно рассматриваются обе фазы системы. Условие (10) записано для компонента, условие (11) – для бинарной системы:


Здесь 
Парожидкостное равновесие идеальной системы (жидкая фаза – идеальный раствор 


Характер отклонения жидкой фазы от идеального поведения качественно и количественно определяется избыточной энергией Гиббса бинарного раствора (рис. 7):

Коэффициенты активности компонентов в жидкой фазе могут быть определены из экспериментальных данных:
— паровая фаза неидеальна (

— паровая фаза идеальна (

или рассчитываются с использованием математической модели парожидкостного равновесия. Допущение об идеальном поведении паровой фазы реальной системы (

Точки экстремумов концентрационных зависимостей избыточной энергии Гиббса, в которых выполняется условие (15):
а ) ) | б ) ) |
в ) )Рис. 7. Бинарные растворы с различным характером отклонения от идеального поведения: а) положительные; б) отрицательные; в, г) смешанные. |


называются псевдоидеальными (рис. 7): х* расположены в области 

Относительная летучесть компонентов бинарной системы определяется следующим образом:

Для случая идеального поведения паровой фазы (14б) имеем:

В случае идеального аналога (смеси) для любого состава 

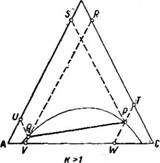
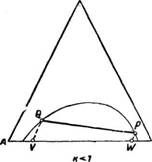
которое выполняется также в псевдоидеальных точках (15) реальных (неидеальных) систем (рис. 8, 9). При неидеальном поведении системы 
На рис. 8 и 9 сплошные линии соответствуют реальным кривым фазового равновесия, пунктирные – их идеальным аналогам, х аз – точки азеотропов, в которых равны составы паровой и жидкой фаз.
Как будет показано ниже (раздел 3), псевдоидеальные точки играют важную роль при исследовании эволюции бинарных азотропов под воздействием температуры (давления).
Рис. 9. Примеры кривых фазового равновесия бинарных систем
со смешанными отклонениями от идеального поведения:
а) зеотропная система; б) моноазеотропная система;
в) биазеотропная система.
2. Фазовое равновесие жидкость – пар бинарных систем
2.1. Основное уравнение фазового равновесия бинарных
двухфазных систем
Для бинарных двухфазных систем уравнение фазового равновесия получено Ван-дер-Ваальсом. Вывод уравнений фазового равновесия жидкость-пар базируется на выражении разности нулевых потенциалов (

Уравнения нулевого потенциала фаз:


Уравнения функции Гиббса фаз:


Из уравнений (20) с учетом 


а) 


а) 


В общем уравнение парожидкостного равновесия бинарной системы для процесса испарения (фазовый переход жидкость пар) можно записать следующим образом:

где множители при дифференциалах температуры и и давления энтропийный и объемный эффекты фазового перехода жидкость пар при образовании 1 моля паровой фазы из бесконечно большого количества жидкой фазы:


Здесь и далее необходимо помнить, что производные берутся при постоянных Т и Р.
Соответственно, для процесса конденсации (фазовый переход пар жидкость) уравнение равновесия запишем в следующем виде:

где 


Отметим, что фазовые эффекты рассмотренных переходов имеют разные знаки, при этом 

В случае однокомпонентных систем все концентрационные слагаемые в выражении (23) исчезают, и оно переходит в известное уравнение Клаузиуса-Клапейрона:

в котором 
При идеальном поведении паровой фазы и условии 

Уравнения Ван-дер-Ваальса содержит информацию о растворе и фазовых переходах и является полной математической моделью фазового равновесия, что позволяет использовать его для математического вывода основных законов ПЖР.
Ниже приведены частные формы уравнения Ван-дер-Ваальса для фазового перехода жидкость пар в бинарной системе. Выражение (23) в изотермических условиях (dТ = 0) преобразуется к виду:

В изобарических условиях (dP = 0), следовательно:

Соответственно, в изотермо-изобарических условиях имеем:

Используя уравнения Ван-дер-Ваальса и его частные формы для равновесия жидкость–пар бинарной системы, дадим математическую интерпретацию известных законов Коновалова и Вревского [1].
Видео:Фазовые равновесия | ФизхимияСкачать
, , . Перегонка жидкостей, ректификация. Учебное пособие (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПЕРЕГОНКА ЖИДКОСТЕЙ, РЕКТИФИКАЦИЯ
Процессы и аппараты химической технологии.
Основы теории, технологический, конструктивный и гидравлический Расчеты ректификационных колонн. Учебное пособие для студентов Химико-Технологического факультета ТПУ, Томск:
Изд-во ТПУ, 2008.- 62с.
В пособии изложены основные положения теории и расчета ректификационных колонн насадочного и тарельчатого типа. Дано физическое обоснование происходящих при этом процессов и определение их количественных характеристик. Приведены основные конструкции аппаратов и их элементов, а также стандартизированные конструктивные размеры, методики основных размеров.
Предназначено для студентов всех специальностей ХТФ.
Рекомендовано к печати Редакционно-издательским отделом Томского Политехнического Университета
Видео:Химическое равновесие. Константа равновесия. 10 класс.Скачать

СОДЕРЖАНИЕ
1. Основы теории процесса ректифиции………………………………. 8
Видео:Уравнения состояния. Фазовое равновесиеСкачать

1.1. Равновесие в системе пар – жикость……………………………….8
Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
1.2. Диаграмма t-x-y бинарной смеси………………………………….10
Видео:Проклятая химическая реакция 😜 #shortsСкачать

1.3. Сущность разделения жидких смесей ректификацией…………..11
Видео:Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

1.4. Установка для непрерывной ректификации бинарной смеси…. 13
2. Основные типовые конструкции ректификационных колонн……….15
Видео:Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

2.1. Насадочные колонны………………………………………………16
Видео:Решение задач на тему: "Нахождение константы равновесия и равновесных концентраций". 1ч. 10 класс.Скачать

2.2. Тарельчатые колонные аппараты………………………………….24
3. Технологический расчет………………………………………………..32
Видео:⚗️ Ректификация. Газовые смеси, фазовое равновесие, диаграммы состояния.Скачать

31.1. Исходные данные к расчету……………………………………….32
Видео:Математика это не ИсламСкачать

3.2. Перечень допускаемых допущений……………………………….32
Видео:Задача химическое равновесие. РАВНОВЕСНЫЕ КОНЦЕНТРАЦИИ и Кр.Скачать

3.3. Материальный баланс……………………………………………. 33
Видео:07.12 Фазовые равновесияСкачать

3.4. Построение фазовых диаграмм…………………………………. 33
Видео:Коробов М. В. - Физическая химия. Часть 1 - Фазовое равновесие. Уравнения Гиббса-Дюгема-МаргулесаСкачать

3.5. Определение рабочего флегмового числа………………………..33
Видео:Гудилин Е. А. - Неорганическая химия I - Фазовые равновесия, диаграммыСкачать

3.6. Определение теоретического числа тарелок по методу Мак-Кеба и Тиле………………………………………………………………………37
Видео:Типы Химических Реакций — Химия // Урок Химии 8 КлассСкачать

3.7. Определение числа единиц переноса……………………………..38
Видео:Гетерогенное равновесиеСкачать

3.8. Определение действительного числа тарелок……………………39
4. Определение геометрических размеров тарельчатых колонн……….42
4.1. Определение диаметра колонны…………………………………..42
4.1.1.Определение объемного расхода паров………………………42
4.1.2. Определение скорости пара…………………………………. 43
4.2. Определение высоты колонны…………………………………….45
5. Определение основных геометрических размеров
5.1. Определение диаметра колонны…………………………………..46
5.1.1. Определение объемного расхода паров……………………. 46
5.1.2.Расчет фиктивной скорости пара……………………………. 46
5.2. Определение высоты слоя насадки………………………………..48
6.2. Определение расхода воды в дефлегматоре……………………. 52
7. Конструктивно-механический расчет…………………………………53
8. Гидравлический расчет…………………………………………………54
8.1.Гидравлическое сопротивление в тарельчатых колоннах………..54
8.2. Гидравлическое сопротивление в насадочных колоннах………..55
9. Расчет тепловой изоляции……………………………………………. 55
10. Блок — схема расчета ректификационной колонны………………….56
11. Вопросы для контроля………………………………………………. 58
Изучение процессов дистилляции (простой и сложной перегонки) целесообразно начинать с рассмотрения физической сущности и отличительных особенностей процессов массопередачи в системе жидкость — пар. Необходимо внимательно изучить диаграммы состояния равновесных бинарных систем и использование основных законов равновесия для определения методов смещения состояния равновесия в заданном направлении. Следует помнить, что основным методом при этом является отвод и подвод теплоты.
Особенностью дистилляционных процессов является то, что вследствие близости значений удельных мольных теплот испарения компонентов смесей, неограниченно растворимых друг в друге, жидкая и паровая фазы обмениваются между собой компонентами в эквимолекулярном соотношении. Из этого следует, что расходы фаз по высоте аппаратов, выраженные в числе кмолей в единицу времени, не изменяются. Поэтому все расчеты процессов перегонки и ректификации, как правило, проводят с использованием мольных расходов и мольных концентраций.
При изучении процессов ректификации особое внимание следует уделить на составление материального и теплового балансов, на уравнения линий рабочих концентраций, на определение минимального и оптимального значений флегмового числа. Следует проанализировать влияние флегмового числа на геометрические характеристики ректификационных колонн и затраты теплоты на проведение процесса.
На заключительном этапе изучения данного раздела необходимо разобраться в основных способах питания ректификационных колонн: исходной смесью, орошение флегмой и подачи пара в куб колонны. Кроме того, следует познакомиться с отличительными особенностями процессов ректификации в установках периодического действия, а также процессов ректификации многокомпонентных смесей.
Основные условные обозначения:
П — общее давление в системе, мм. рт. ст. или Па;
Фх, Фу — соответственно жидкая и газовая фазы;
Р* — равновесное давление компонента в паре, мм. рт. ст. или Па;
Ро — давление насыщенного пара чистого компонента, мм. рт. ст. или Па;

У* — равновесное содержание компонента в паре, кмоль/кмоль;

tкип. — температура кипения, 0С;
F — производительность колонны по исходной смеси, кмоль/с;
Р — производительность колонны по продукту, кмоль/с;
W — производительность колонны по кубовому остатку, кмоль/с;
М — мольная масса смеси, кг/кмоль;
G — нагрузка колонны по пару, кмоль/с;
R — флегмовое число (R=Ф/Р);
f — расходный коэффициент (f=F/P);
r — удельная теплота конденсации, Дж/кг или Дж/кмоль;
С — удельная массовая теплоемкость, Дж/(кг×0К);
N, NД — соответственно число теоретических и действительных тарелок;
n0x, noy — общее число единиц переноса по фазе Фх и фазе Фу;
m — коэффициент динамической вязкости, Па×с;
V — объемный расход, м3/с;
r — плотность, кг/м3;
Т0=273,150 — нормальная температура, 0К;
Т — температура вещества, 0К; Т=t0C + T0;
w — фиктивная рабочая скорость, отнесенная к полному сечению аппарата, м/с;
wпред. — предельно-допустимая скорость, м/с;
a — удельная поверхность насадки, м2/м3;
g — ускорение силы тяжести, м/с2;
Re — критерий Рейнольдса;
Pr’ — диффузионный критерий Прандтля;
Dп, Dж — коэффициенты диффузии, соответственно в паре и в жидкости, м2/с;
hx, hy — частные высоты единиц переноса по фазам Фх и Фу;
S — площадь сечения колонны;
L, G — соответственно расходы жидкости и пара, кг/с (уравнение 5.2);
m — коэффициент распределения;
b — температурный коэффициент для расчета коэффициента диффузии D: 
I, i — энтальпии потоков, Дж/кг;
Dг. п. — расход греющего пара, кг/с;
К — коэффициент теплопередачи, Вт/(м2.К);
Dtср. — средняя движущая сила процесса теплопередачи;
l — коэффициент теплопроводности, Вт/(м×К);
DР — перепад давлений /гидравлическое сопротивление/, Па;
s — поверхностное натяжение, н/м.
Индексы: НК — низкокипящий компонент; ВК — высококипящий компонент; i — компонент; кип. — кипение жидкости; ср. — среднее значение параметра; в — верх колонны; н — низ колонны; ж — жидкость; п — пар; см. — смесь компонентов; ст. — стенка; окр. — окружающая среда.
Видео:О равновесии в химии и химической технологииСкачать

ВВЕДЕНИЕ
Настоящее учебное пособие разработано на основе рабочей и типовой программы курса «Процессы и аппараты химической технологии» и предназначены в помощь студентам при изучении теоретического курса, при выполнении курсовых и дипломных проектов.
В данном пособии приведены самые необходимые сведения по теории процесса массопередачи в системе пар-жидкость и освещены главные вопросы технологического и гидравлического расчетов. Конструктивно-механический расчет приведен частично и касается вопросов определения размеров отдельных элементов массообменных аппаратов. Приводится необходимый минимум справочных данных по характеристикам наиболее распространенных в химической промышленности нормализованных контактных устройств насадочного и тарельчатого типов.
Процесс ректификации по своим физико-химическим свойствам и методам расчета относится к одному из наиболее сложных массообменных процессов. Поэтому, прежде чем приступить к выполнению расчетов, всем студентам рекомендуется на первом этапе предварительно повторить основные вопросы теории процесса ректификации, уделяя при этом особое внимание физическому смыслу не только основных закономерностей, но и отдельных параметров процесса.
Напоминание! Все расчеты следует выполнять в системе единиц измерений СИ.
Видео:Коробов М. В. - Физическая химия. Часть 1 - Фазовое равновесиеСкачать

1. ОСНОВЫ ТЕОРИИ ПРОЦЕССА РЕКТИФИКАЦИИ
Видео:Румянцева М.Н.- Общая и неорганическая химия. Лекции - 4.Фазовые равновесияСкачать

1.1 Равновесие в системе пар-жидкость
Основные законы равновесия:
1. Правило фаз Гиббса:
Правило определяет число независимых параметров системы, которые можно изменять произвольным образом, не изменяя при этом состояния равновесия системы. Для системы пар-жидкость (Ф=2) число ступеней свободы равно числу компонентов К, т. е. С=К. В простейшем случае для бинарных смесей, состоящих из низкокипящего (НК) и высококипящего (ВК) компонентов число степеней свободы равно двум, т. е. С=2. Из этого следует, что равновесное состояние системы определяется только двумя параметрами из трех. При этом, если один из них зафиксирован, что чаще всего наблюдается на практике (например общее давление П=const), то остается только один параметр. В частности, в системе пар-жидкость это температура (при этом концентрации фаз, как третья степень свободы, устанавливаются на определенном уровне) или концентрация фаз (при этом устанавливается температура фаз на определенном уровне). Следует помнить, что равновесие в системе пар-жидкость соответствует состоянию кипения жидкости и равновесного с ней насыщенного пара, при этом температура пара равна температуре жидкости.

Парциальное давление компонента в паре, находящемся в равновесии с жидкостью, равно произведению давления насыщенного пара чистого компонента на его мольную долю в жидкости (i — компонент смеси).
2. Закон Дальтона:
Общее давление парогазовой смеси равно сумме парциальных давлений компонентов этой смеси. Учитывая, что åуi=1, следствием из закона Дальтона является:
Парциальное давление компонента в парогазовой смеси равно произведению общего давления этой смеси на его мольную долю в смеси.
3. Закон Рауля-Дальтона:

Данный закон устанавливает соотношение равновесных концентраций компонентов в паре (У*i) и в жидкости (Хi). Для бинарных смесей, состоящих из НК и ВК уравнение1.5 выражается через концентрации НК в фазах и с учетом уравнения 1.3 принимается вид:

Смеси, подчиняющиеся уравнению 1.5 носят название идеальных смесей. известно много реальных смесей не подчиняющихся закону Рауля. Для таких смесей вводят понятие активности компонента в растворе, т. е.:

Фазовое равновесие
Диаграммы фазового равновесия. В процессе экстракции участвуют по крайней мере три вещества: смесь взаимно растворимых двух веществ, подлежащая разделению, и растворитель, не полностью смешивающийся со смесью и способный растворять один компонент смеси. В данном случае имеет место тройная или трехкомпонентная система, общий состав которой всегда однозначно можно представить точкой в равностороннем треугольнике.
Графическое представление общего состава тройных смесей дано на рис. 412, а. Обычно принято точку, соответствующую чистому растворителю С, помещать в правом нижнем углу треугольника, точку, соответ-
Рис. 412. Графическое представление тройной смеси: А—Общий состав смеси; б—Правило пропорциональности.
Ствующую чистому компоненту А с ограниченной растворимостью,—в * левом нижнем углу и точку, соответствующую чистому компоненту В, полностью растворимому в растворителе,—в вершине треугольника. Состав смеси будем выражать в весовых долях компонентов, соответственно считая, что длина каждой стороны треугольника равна единице и что точки, лежащие непосредственно на сторонах треугольника, представляют собой составы бинарных смесей в пределах от 0 до 1,0.
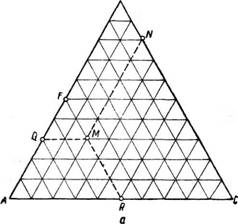
Любая точка внутри треугольника показывает содержание всех трех компонентов смеси, выраженное в весовых долях. Если точку М внутри треугольника (рис. 412, а) соединить с точками, лежащими на каждой из его сторон, линиями, параллельными соответствующим сторонам треугольника, то сумма длин соединяющих линий будет для любой точки внутри треугольника равна стороне треугольника, т. е. при принятых нами выражениях состава смеси в весовых долях всегда будет равна
Единице. __ _____ _____ _____ _____ _____
Сопоставление общего материального баланса смеси с материальным балансом компонентов, составляющих смесь, позволяет вывести следую
щее положение: при расслаивании смеси F на две фазы Q и R точки наг треугольной диаграмме, представляющие состав исходной смеси и составы фаз Q и R, лежат на одной прямой и отношение веса фазы Q к весу фазы R равно отношению длин отрезков QS и RS (рис. 412, б).
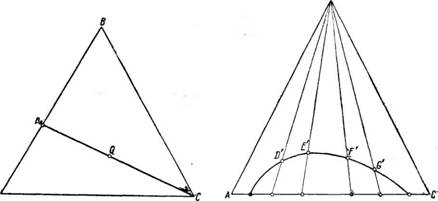
Эти положения являются общими и поэтому справедливы и для случаев, когда к смеси двух компонентов добавляется третий. Так, если к смеси А и В, состав которой выражается точкой Р на рис. 413, добавлен компонент С, то состав тройной смеси выразится точкой на прямой PC, причем количество добавленного компонента С будет относиТься к количеству начальной смеси как отношение длин отрезков PQ : QC.
Рис. 413. Диаграмма общего состава Трой — Рис. 414 Бинодальная кривая в треугольной смеси, полученной добавлением к Би — Ной диаграмме, нариой смеси третьего компонента.
Допустим (рис. 414), что имеется бинарная смесь компонентов А И С, обладающих ограниченной растворимостью; состав смеси задан точкой F.
Эта смесь расслаивается на две фазы Р и Q с составами, отвечающими точкам Q и Р, в отношении FQ : FP. При добавлении по каплям к этой смеси третьего компонента В, полностью смешивающегося как с компонентом А, так и с компонентом С, все бинарные смеси компонентов А и С, состав которых представлен на диаграмме точками, лежащими между Q и Р, расслаиваются на две фазы с составами, отвечающими точкам Q и Р.
Рассмотрим смесь, общий состав которой задан точкой D. Эта смесь расслаивается на фазы Q и Р в отношении DQ : DP. При добавлении к смеси с составом D компонента В по каплям отношение фаз Q: Р постепенно изменяется, при этом одна из фаз будет уменьшаться до тех пор, показне будет достигнуто состояние, при котором к смеси будет добавлено такое большое количество компонента В, что фаза с высоким содержанием компонента С полностью исчезнет. При этом смесь станет гомогенной. Это состояние обозначено на диаграмме точкой D‘, которая является точкой смешения (точкой расслаивания) в тройной системе компонентов А,
Путем добавления компонента В к другим гетерогенным смесям компонентов А и С (например, Е’, F‘, G‘ . ) можно для любой бинарной смеси подобрать такое количество компонента В, при котором полученные тройные смеси (E‘,F‘F G‘. ) будут гомогенными. При таком «титровании» компонентом В большого количества бинарных смесей, расположен
ных между Q и Р, получается ряд точек! смешения, которые образуют кривую QD‘E‘F‘G Р. Эта кривая называется бинодальной. Так как растворимость вещества в значительной степени зависит от температуры, для каждой температуры будет своя бинодальная кривая, а любая бинодальная кривая относится только к одной определенной температуре.
Рис. 415. Линии сопряжений в треугольной диаграмме.
В области, ограниченной прямой Qp и бинодальной кривой, система всегда гетерогенна (область расслаивания), в остальной части диаграммы— система гомогенна. В гетерогенной области любая система будет расслаиваться на две сосуществующие фазы, составы которых изображаются точками, лежащими на бинодальной кривой. Линия, которая соединяет
Точки, представляющие составы в двух сосуществующих фаз, назы-
/Вается линией сопря — ж е н и я.
, Наклон линии сопряжения
(рис. 415) зависит от природы
компонентов и определяется вели-
чиной коэффициента распределе-
/ ния k, представляющего собой
/ отношение содержаний распреде-
/ р fy__________ — ляемого между фазами компонен-
Концентрации могут быть выражены в различных единицах: Рис. 416. Линии сопряжения и критическая весовых, объемных, молярных и точка смешения. др., поэтому при решении прак
Тических задач следует соответственно переводить найденное значение K в те единицы, в которых проводится расчет.
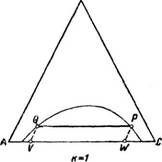
В тройной системе коэффициент распределения обычно не имеет постоянного значения, так как он зависит от состава фаз, как это показано на рис. 416. Добавляя к гетерогенной смеси веществ А и С увеличивающиеся количества компонента В и определяя каждый раз составы сосуществующих фаз, найдем, что общий состав гетерогенной смеси изменяется по прямой R, Rt, R2, Rs. Гетерогенные системы, состав которых представлен точками на этой прямой, расслаиваются на соответствующие-
сосуществующие фазы Р и Q, Рх и Qlt Р2 и Q2 и т. д. При этом состав фазы с высоким содержанием компонента А изменяется по кривой Р, Рх, Р«, Р5. а состав фазы с высоким содержанием С—по кривой Q, Qlt Q2. Q3. В точке К пересечения прямой RRyR^R^.. и бинодальной кривой будет иметь место только одна фаза, т. е. смесь станет гомогенной. Такую точку смешения К, в которой составы обзих фаз становятся одинаковыми, называют критической точкой смешения. Для этой точки коэффициент распределения имеет значение, равное единице.
Рис. 417. Определение критической точки смешения (К).
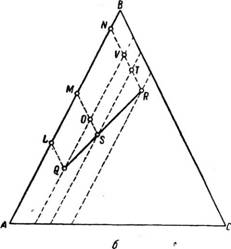
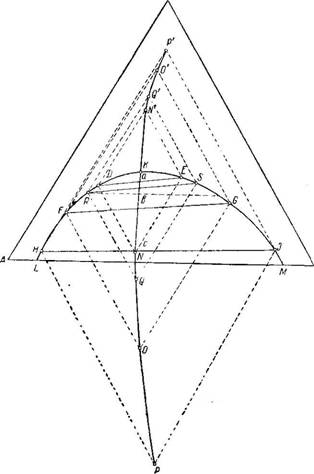
Критическую точку смешения на бинодальной кривой сравнительно просто найти путем построения на треугольной диаграмме.
Положим, что для данной трехкомпонентной смеси веществ А, В и С положение бинодальной кривой и линий связи A, B И с в треугольной диаграмме известны (рис. 417). Через точки D, Е, F, G, Н и / проведем линии, параллельные боковым сторонам треугольника. Получим точки Р, О, N. N‘, О’, Р’. Соединяя эти точки, получим соединительную линию, которая пересекает бинодальную кривую в точке, являющейся критической точкой К смешения для данной тройной системы.
При помощи соединительной линии можно найти линии сопряжения. Допустим, что нужно узнать, какая фаза сосуществует с фазой R (см. рис. 417). Проводя из точки R Линию, параллельную АВ, найдем точку пересечения этой линии с соединительной линией (точка Q‘). Проведя из точки Q‘ Линию, параллельную ВС, найдем на бинодальной линии точку пересечения S, Которая и указывает на состав фазы S, Сосуществующей с фазой R. Линия RS И будет линией сопряжения.
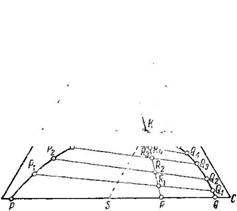
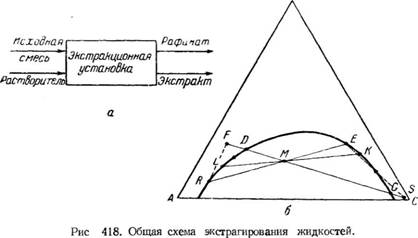
Ступень изменения концентрации при экстрагировании. При экстрагировании жидкости жидкостью в общем случае, как это схематически представлено на рис. 418, а, на экстрагирование поступает исходная
Смесь, представляющая собой гомогенную жидкую смесь двух или большего числа компонентов, и растворител ь—жидкость, которая не смешивается с исходной смесью и обладает способностью избирательно растворять компоненты исходной смеси. В результате взаимодействия ‘ ‘ исходной смеси с растворителем образуются две новые механически разделимые жидкие фазы: экстракт, представляющий собой раствор 9 одного из наиболее растворимых компонентов исходной смеси в растворителе, и р а ф и н а т—остаток исходной смеси, более или менее освобожденный от компонента, извлеченного растворителем.
В результате взаимодействия исходной смеси с растворителем получается двухфазная система, первоначально состоящая из слоя растворителя и слоя исходной смеси. Так как концентрация распределяемого между фазами наиболее легко растворимого компонента в исходной смеси больше равновесной, а в растворителе—меньше равновесной, компонент, наиболее растворимый в данном растворителе, будет переходить из исходной смеси в растворитель до тех пор, пока не будет достигнуто фазовое равновесие между двумя жидкими фазами—экстрактом и рафинатом.
Такой однократный контакт между исходной смесью и растворителем, в результате которого устанавливается полное фазовое равновесие между экстрактом и рафинатом, представляет собой ступень изменения концентрации при экстрагировании, или теоретическую ступень экстракции.
Диаграмма однократного контакта, соответствующего одной ступени изменения концентрации при экстрагировании, представлена на рис. 418, б, где линия RDEG Представляет собой бинодальную кривую равновесия,
39 А. г. Касаткин.
F—точку, соответствующую составу исходной смеси, 5—точку, соответствующую составу растворителя, Е и R—точки, соответствующие равновесным составам экстракта и рафината.
F—вес исходной смеси в кгс; S—вес растворителя в кгс Е—вес экстракта в кгс R—вес рафината в кгс xAF—концентрация компонента А в исходной смеси; xAs—концентрация компонента А в растворителе; Хвf—концентрация компонента В в исходной смеси; Хвs—концентрация компонента В в растворителе; М—общий вес смеси, получающейся от смешения исходной смеси с растворителем, в кгс;
Материальный баланс процесса выражается уравнением
М = F + 5 = R + Е (3—269)
На основании правила пропорциональности, изложенного выше, отношение между весовыми количествами растворителя и исходной смеси может быть выражено равенством
Последнее равенство дает возможность определить положение на диаграмме точки М, соответствующей составу смеси Хм-
Из уравнения материального баланса компонентов А и В: