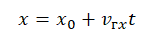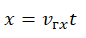Равноускоренное движение уравнение x t

Видео:Физика - уравнения равноускоренного движенияСкачать

Равноускоренное движение: формулы, примеры

Видео:Равноускоренное движение. Вывод формулСкачать

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

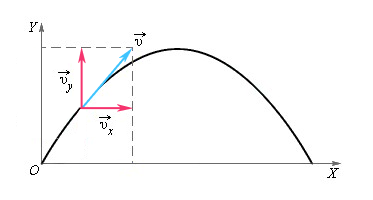
Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

​​​​​​​

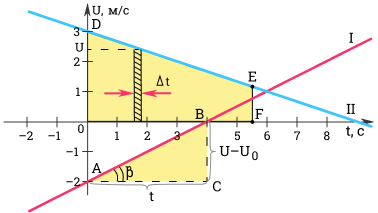
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Видео:Выполнялка 168. Равноускоренное движение. Как строить графики.Скачать

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Видео:Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Прямолинейное равноускоренное движение. Формулы и решение задач

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Видео:Уравнение координат при равноускоренном движенииСкачать

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

Вам будет интересно: Методика ШТУР: расшифровка аббревиатуры, особенности проведения теста, итоговый анализ и результаты

В первую очередь это пройденный путь. Будем его обозначать буквой S. Согласно определению, путь — это расстояние, которое тело прошло вдоль траектории перемещения. В случае прямолинейного движения траектория представляет собой прямую линию. Соответственно, путь S — это длина прямого отрезка на этой линии. Он в системе физических единиц СИ измеряется в метрах (м).

Вам будет интересно: «Рубаха-парень»: значение в прошлом и сейчас

Скорость или как часто ее называют линейная скорость — это быстрота изменения положения тела в пространстве вдоль его траектории перемещения. Обозначим скорость буквой v. Измеряется она в метрах в секунду (м/с).

Ускорение — третья важная величина для описания прямолинейного равноускоренного движения. Она показывает, как быстро во времени изменяется скорость тела. Обозначают ускорение символом a и определяют его в метрах в квадратную секунду (м/с2).

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Видео:Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать

Связь скорости и ускорения

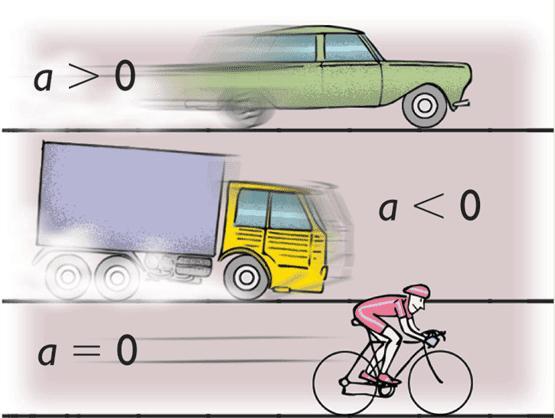
Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

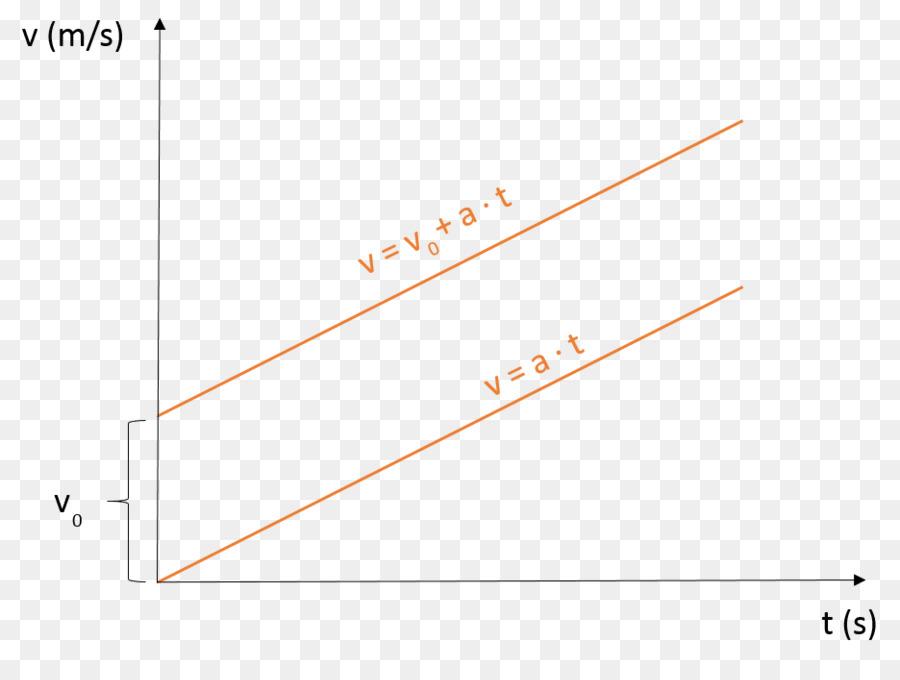
Здесь второе слагаемое описывает прирост скорости за каждый промежуток времени. Поскольку v0 и a являются постоянными величинами, а v и t — это переменные параметры, то графиком функции v будет прямая, пересекающая ось ординат в точке (0; v0), и имеющая некоторый угол наклона к оси абсцисс (тангенс этого угла равен величине ускорения a).

На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

Этот вид движения называется прямолинейным равнозамедленным.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v0 * t + a * t2 / 2.

Первый член соответствует равномерному движению без ускорения. Второй член — это вклад в пройденный путь чистого ускоренного движения.

В случае торможения движущегося объекта выражение для пути примет вид:

S = v0 * t — a * t2 / 2.

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

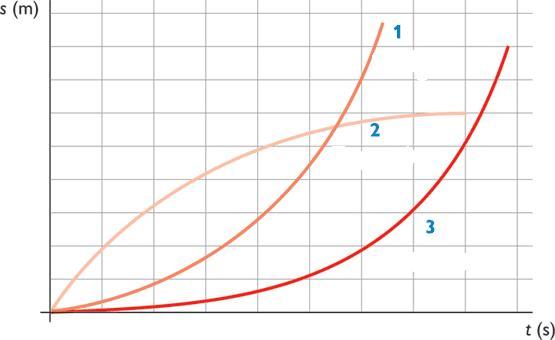
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Далее в статье решим три разные задачи на использование приведенных формул.

Видео:Решение задач. Равноускоренное движение (достаточный уровень)Скачать

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

При этом скорость, которую он наберет за 20 секунд, равна:

Тогда искомое время движения t можно вычислить по следующей формуле:

t = (S — S1) / v + t1 = (S — a * t12 / 2) / (a * t1) + t1.

Здесь S — расстояние между A и B.

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Видео:О терминах равноускоренное и равнозамедленное движениеСкачать

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

Тормозной путь S можно рассчитать по следующей формуле:

S = v0 * t — a * t2 / 2.

Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

S = v0 * t — v0 * t / 2 = v0 * t / 2.

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Видео:прямолинейное РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ | формулы кинематикиСкачать

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Искомую скорость можно рассчитать по формуле:

Время падения тела определим из соответствующего выражения для пути S:

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

Видео:Механика. Равноускоренное движение. Уравнения изменения скоростиСкачать

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Видео:Решение графических задач на равномерное движениеСкачать

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 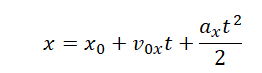Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

🌟 Видео

Прямолинейное равномерное движение | Физика ОГЭ 2024 | УмскулСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Скорость прямолинейного равноускоренного движения. График скорости | Физика 9 класс #6 | ИнфоурокСкачать

§6. Физика 9 кл. Скорость прямолинейного равноускоренного движения. График скорости.Скачать

Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать