презентация к уроку по алгебре (10, 11 класс)
Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Иррациональные неравенства с примерами решения
- Способы решения иррациональных неравенств
- Пример №1
- Пример №2
- Какие неравенства называются иррациональными
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Алгебра и начала математического анализа. 10 класс
- 💡 Видео
Видео:Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Скачать:
| Вложение | Размер |
|---|---|
| 93_uravneniya_i_sistemy_uravneniy.docx | 127 КБ |
Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Предварительный просмотр:
Тема: Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.
Рассмотреть способы решения рациональных, иррациональных, показательных и тригонометрических уравнений и неравенств.
- Ознакомьтесь с алгебраическими системами уравнений по ссылке:
- Ознакомьтесь со способами решения показательных уравнений и систем уравнений
- Ознакомьтесь со способами решения иррациональных уравнений
- Ознакомьтесь со способами решения тригонометрических уравнений
- Ознакомьтесь со способами решения систем уравнений
- Ознакомьтесь со способами решения систем тригонометрических уравнений
- Решите графически систему уравнений
- Решите систему уравнений:
а) 
- Площадь прямоугольника равна 36см 2 , а его периметр – 24см. Найдите стороны прямоугольника.
4. Постройте график уравнения (3х+2)(у+х 2 -4)=0
5. Решите систему уравнений
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

По теме: методические разработки, презентации и конспекты
Урок-зачет в 10 классе по теме «Тригонометрические уравнения, неравенства, системы уравнений»
Цель урока: Проверить знания и умение применений формул для решения тригонометрических уравнений.Вид работы: «Смотр знаний», состоящий из 5 этапов, проводится в течение двух уроков. За каждый эт.
Конспект урока по теме: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “
Разобраны свойства функции sinx. Приведено решение уравнения sinx=a. Разобраны 4 примера.
Тема 17. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Решение простейших тригонометрических уравнений. Общий приём. Метод разложения на множители.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э.
Тест по темам « Решение уравнений и их систем», «Решение неравенств и их систем» и «Решение уравнений, неравенств, систем неравенств с модулем».
Задания теста соответствуют содержанию учебника «Алгебра. 9 класс : учеб. для учащихся общеобразовательных учреждений / Ю. Н. Макарычев , Н. Г. Миндюк , К. И. Нешков , И. Е. Феоктист.
Урок-лекция по алгебре и началам анализа «Решение тригонометрических уравнений, неравенств и систем уравнений»
В данной лекции подробно указаны все способы решения тригонометрических уравнений, неравенств и систем уравнений.
Урок-зачет по теории и практике по теме «Тригонометрические уравнения, неравенства и системы уравнений»
В данном уроке представлены вопросы к зачету и практические задания.
Системы уравнений с двумя переменными. Графический метод решения систем двух линейных уравнений с двумя переменными
Урок объяснения нового материала по учебнику «Алгебра, 7 класс» А.Г. Мерзляк, параграф 26. Презентация составлена для объяснения новой темы в Zoom при дистанционном обучении.
Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Иррациональные неравенства с примерами решения
Неравенства, содержащие переменную под знаком радикала, называются иррациональными неравенствами.
Содержание:
Решение иррациональных неравенств также ищут на множестве действительных чисел и, используя свойства корня и неравенств, сводится к решению системы рациональных неравенств.
Пример: Решите неравенство
Решение: чтобы найти множество решений данного неравенства на множестве допустимых значений, т. е. при условии
Каждое неравенство системы решим методом интервалов и найдем пересечение полученных решений:
Пример: Решите неравенство
Решение: рассмотрим два случая, в зависимости от знака правой части.
1) при 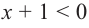
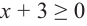
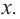
Ее решением является промежуток
2) при 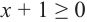
Ее решением является промежуток
Решением заданного неравенства является
Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Способы решения иррациональных неравенств
С действием возведения в степень связаны разные виды выражений. Будем рассматривать выражения с переменными, при образовании которых используются действия сложения, вычитания, умножения, деления и возведения в степень, причем возведение в степень хотя бы один раз применено к выражению с переменной.
Если показатель степени целый, то возникает рациональное выражение, если дробный, то — иррациональное выражение, а если иррациональный, то — трансцендентное выражение.
К трансцендентным выражениям приводят и действия нахождения значений синуса, косинуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса, арккотангенса. Рациональные и иррациональные выражения вместе составляют множество алгебраических выражений.
выражения (1) и (2) являются рациональными, выражения (3) и (4) — иррациональными, выражения (5) и (6) — трансцендентными, а выражения (1)—(4) — алгебраическими.
В зависимости от того, из каких выражений составлено уравнение, говорят о рациональных, иррациональных, трансцендентных уравнениях.
уравнения (1) и (2) являются рациональными, уравнения (3) и (4) — иррациональными, а уравнения (5) и (6) — трансцендентными.
Так же говорят о рациональных, иррациональных, трансцендентных неравенствах.
В этом параграфе рассматривается решение иррациональных уравнений и неравенств. При их решении нужно следить за тем, какие преобразования выполняются при этом.
Утверждение 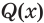
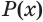
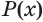
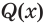
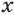
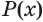
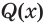
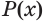
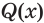
Утверждение 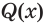
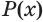
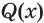
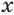
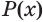
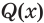
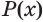

Отношения равносильности и следования связаны:
При решении иррациональных неравенств нужно учитывать, что проверка подстановкой найденного множества чисел обычно невозможна из-за его бесконечности. Поэтому при решении неравенств нужно следить за равносильностью проводимых преобразований.
Теорема:
Верны следующие равносильности:
Доказательство проводится по схеме, использованной при доказательстве теоремы 9 с применением соответствующих свойств числовых неравенств.
Пример №1
Решим неравенство 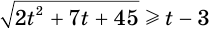
Первую систему можно заменить равносильной системой 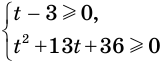


Вторая система совокупности равносильна системе 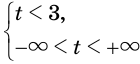
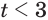
Решения данного неравенства получим, когда объединим решения 
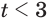
Ответ. 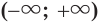
Пример №2
Решим неравенство 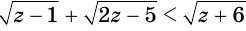
Обратим внимание на то, что на области определения левая и правая части данного неравенства обе неотрицательны, поэтому оно равносильно системе неравенств
решение которой следующее:
Ответ. 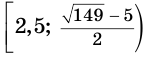
Видео:11 класс, 26 урок, Равносильность уравненийСкачать

Какие неравенства называются иррациональными
В этой лекции мы будем рассматривать неравенства, содержащие переменную (неизвестное) под знаком корня. Такие неравенства называются иррациональными.
При решении иррациональных неравенств часто используют подход, который мы уже применяли, решая иррациональные уравнения. Он состоит в замене исходного неравенства равносильным ему неравенством (системой или совокупностью неравенств).
Пример №3
Решение:
а) Учитывая свойства корня нечетной степени, получаем:
б) По определению корня четной степени значения выражения
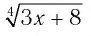
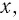
выражение имеет смысл, т. е. когда значения подкоренного выражения неотрицательны. Таким образом, имеем:
Ответ:
Пример №4
Решение:
а) По определению корня четной степени значения выражения 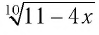
б) Поскольку обе части неравенства 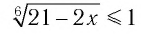
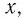
Ответ:
При решении иррациональных неравенств часто используется также метод интервалов.
Пример №5
Решить неравенство
Решение:
Обозначим 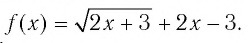
Таким образом,
Найдем нули функции 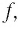
Проверка:
Значит, 0,5 — единственный нуль функции
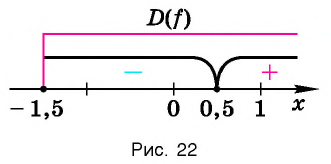
Отметим нуль функции 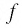
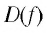
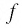
Используя рисунок 22, запишем решение неравенства
Ответ:
Пример №6
Решить неравенство
Решение:
Решение этого примера аналогично решению примера 3.
Используя рисунок 22, записываем решение неравенства
Ответ:
▲ При решении иррациональных неравенств часто используются следующие утверждения о равносильности неравенств и систем неравенств:
Решим пример 3, используя равносильность (1):
Ответ:
Решим пример 4, используя равносильность (2):
Ответ:
Для решения заданий такого типа, как, например, в 1.265, можно использовать следующие утверждения о равносильности:
Аналогичные утверждения можно записать и для неравенств
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Производная в математике
- Как найти производную функции
- Асимптоты графика функции
- Касательная к графику функции и производная
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Свойства и график функции y=ⁿ√x (n>1, n∈N)
- Иррациональные уравнения
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №19. Равносильные уравнения и неравенства
Перечень вопросов, рассматриваемых в теме
1) понятие равносильного уравнения;
2) понятие равносильного неравенства;
3) понятие уравнения-следствия;
4) основные теоремы равносильности.
Глоссарий по теме
Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.
Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Определение. Два уравнения с одной переменной
f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.
Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
1) Уравнения 
2) Уравнения 

3) А вот уравнения 
Из определения равносильности следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения, и наоборот.
Решение уравнения осуществляется в три этапа.
Первый этап — технический. На этом этапе осуществляют преобразования по схеме (1) → (2) → (3)→ (4) → . и находят корни последнего (самого простого) уравнения указанной цепочки.
Второй этап — анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.
Третий этап — проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.
Реализация этого плана связана с поисками ответов на четыре вопроса.
- Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
- Какие преобразования могут перевести данное уравнение в уравнение-следствие?
- Если мы в конечном итоге решили уравнение-следствие, то как сделать проверку в случае, когда она сопряжена со значительными вычислительными трудностями?
- В каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?
Из курса средней школы мы знаем, что можно сделать следующие преобразования уравнений: любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Обе части уравнения можно умножить или разделить на одной и то же число, не равное нулю.
Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называет следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнения называется следствием первого уравнения.
Из этого определения и определения равносильности уравнений следует, что:
- если ва уравнения равносильны, то каждое из них является следствием другого;
- если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.
При решении уравнений главное- не потерять корни, а наличие посторонних корней можно установить проверкой. Поэтому важно следить за тем, чтобы при преобразовании уравнения каждое следующее уравнение было следствием предыдущего.
Стоит отметить, что посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное; а вот потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.
Итак, сформулируем основные теоремы, которые используются при решении равносильных уравнений:
Определение. Областью определения уравнения f(х) = g(х) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения
Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2. Если обе части уравнения возвести в одну и туже нечетную степень, то получится уравнение, равносильное данному.
Теорема 3. Показательное уравнение 
равносильно уравнению f(x) = g(х).
Теорема 4. Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:
а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(х)
б) нигде в этой области не обращается в 0, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.
Следствием теоремы 4: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5. Если обе части уравнения f(x)=g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение 
Краткая запись теорем 4, 5.
4. f(x) = g(x) ⇔h(x)f(x) = h(x)g(x), где h(x) ≠0
и h(x) имеет смысл в ОДЗ данного уравнения.
5. f(x) = g(x) ⇔ 
и n=2k (чётное число).
Например, х – 1 = 3; х = 4
Умножим обе части на (х – 2):
(х – 2)(х – 1) = 3(х – 2); х = 4 и х = 2 – посторонний корень⇒ проверка!
Равносильность неравенств с неизвестным определяется аналогично.
Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.
Разбор решения заданий тренировочного модуля
Решим уравнение:
Возведем в квадрат обе части уравнения, получим:


- Неравенства
и x-3 x-1 не равносильны, так как решениями первого являются числа x 1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.
💡 Видео
Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Равносильные уравнения, неравенстваСкачать

ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Как проверяют учеников перед ЕНТСкачать

Решение неравенства методом интерваловСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Как решают уравнения в России и СШАСкачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

решение УРАВНЕНИЙ решение НЕРАВЕНСТВ 10 11 классСкачать

Иррациональные неравенства. 11 класс.Скачать









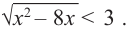
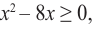
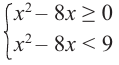
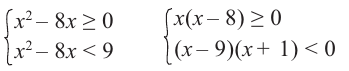
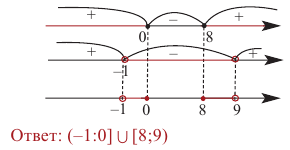
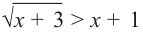
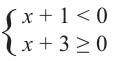
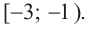
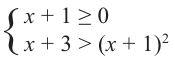
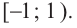
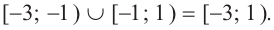
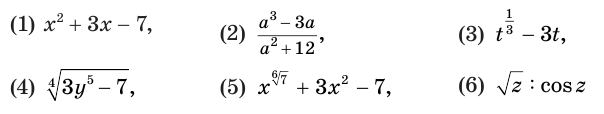
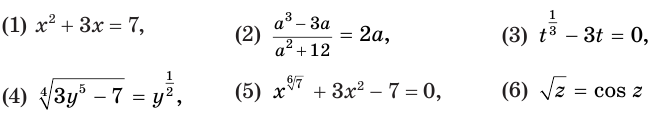
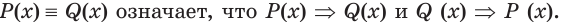
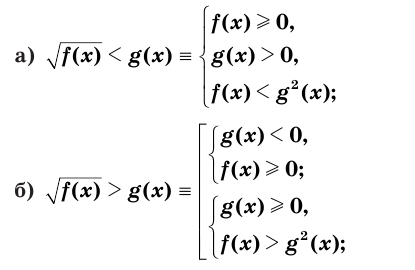
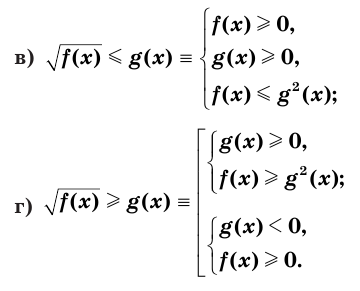
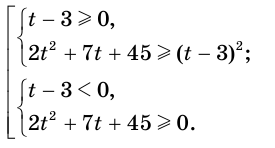
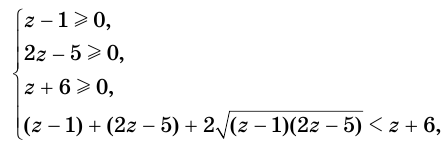
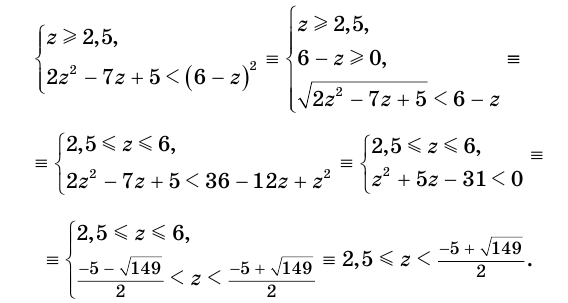

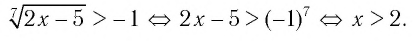
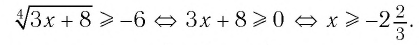
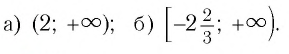

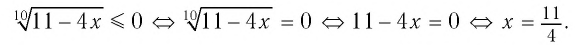
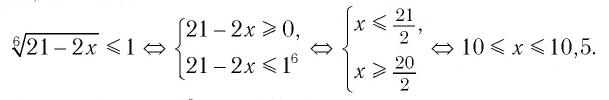
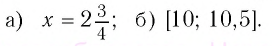
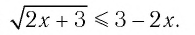
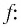
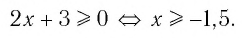
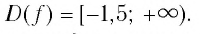
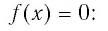
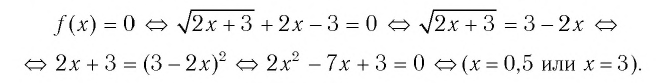
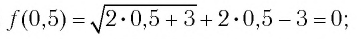
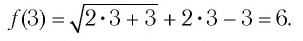
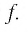
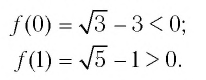
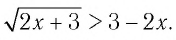
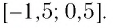
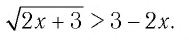
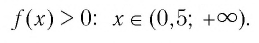
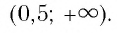
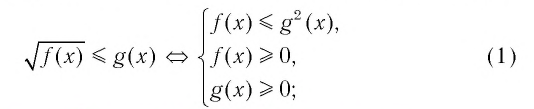
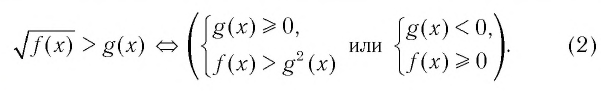
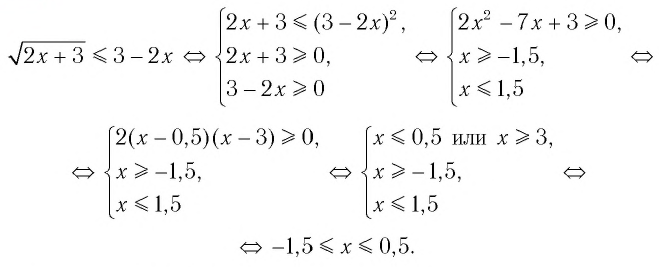
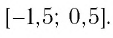
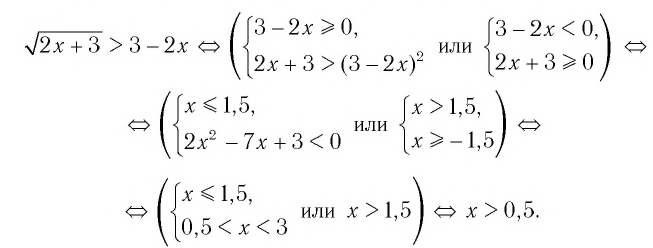
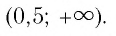
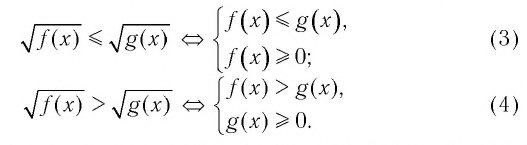
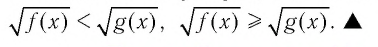

 и x-3 x-1 не равносильны, так как решениями первого являются числа x 1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.
и x-3 x-1 не равносильны, так как решениями первого являются числа x 1, а решениями второго- числа x>-1. При решении неравенств обычно данное неравенство преобразуется в ему равносильное.