Рациональные уравнения как математические модели реальных ситуаций 8 класс мерзляк

Просмотр содержимого документа
«Урок по теме » Рациональные уравнения как математические модели реальных ситуаций»»

Тема урока: « Рациональные уравнения как математические модели реальных ситуаций»

— отработка навыков составления математической модели задачи в виде дробных рациональных уравнений;

— развитие способности к содержательному обобщению и рефлексии;

— развитие алгоритмического мышления;

— повышение интереса к решению математических задач.

Цель как деятельность учеников: научиться составлять математические модели реальных ситуаций.

Задачи:

1. Обеспечить учащимся понимание уравнения как математической модели некоторой жизненной ситуации, описанной в текстовой задаче.

2. Формировать познавательные, регулятивные, коммуникативные и личностные УУД как цели урока.

Ход урока:

1) Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Здравствуйте, ребята. Ещё начиная с начальной школы, вы учились решать уравнения. Для этого с каждым годом вы обучались всё новым и новым методам и способам решения.

— Какую тему мы изучили? (рациональные уравнения). Какие рациональные уравнения вы научились решать?

— Какую тему обычно изучают после окончания изучения уравнений? (решение задач с помощью уравнений).

— Как мы называли составленные уравнения в решении простейших жизненных задач, реальных ситуаций? (математические модели)

— Определите тему сегодняшнего занятия. (Рациональные уравнения как математические модели реальных ситуаций).

Итак, тему урока определили.

2) Фронтальный опрос, устная работа с классом.

На этапе актуализации идёт повторение изученного материала, необходимого для получения новых знаний, и выявление затруднений в индивидуальной деятельности каждого учащегося.

Сначала мы повторим все о дробных рациональных уравнениях. (Один ученик вызывается к доске для решения уравнения:

Ответ. )

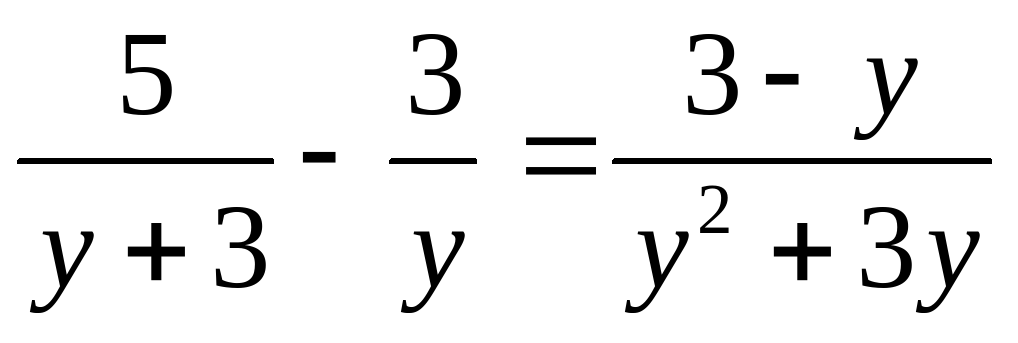
Ответьте, пожалуйста, на следующие вопросы:

— Какие уравнения называются дробными рациональными?

— Что необходимо знать для успешного решения дробных рациональных уравнений? (Общий знаменатель дробей, входящих в уравнения)

— Расскажите алгоритм решения дробных рациональных уравнений.

1) Найти общий знаменатель дробей, входящих в уравнение.

2) Умножить обе части уравнения на общий знаменатель.

3) Решить получившееся целое уравнение.

4) Исключить из его корней те, которые обращают в нуль общий знаменатель.

5) Записать ответ.

— Найти общий знаменатель дробей в каждом из уравнений:

Ответ: 5х-2 или 2-5х

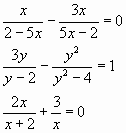
— Верно ли решены уравнения?

а) 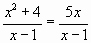х1 =1, х2=4

Ответ: нет, корень х=1 — посторонний.

б) 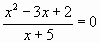х=1

Ответ: нет, есть еще один корень Х=2.

— Проверить решение уравнения, записанного на доске.

— Мы научились решать дробные уравнения.

А для чего они нужны? Какие задачи приводят к их появлению?

— Такие ,в которых одна величина выражается через другие при помощи дробного выражения.

Например: время = ; ;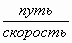

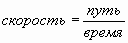
Cторона прямоугольника= ;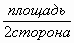

;

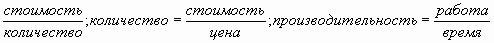
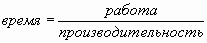
и другие.

Итак, вы могли убедиться, что людям разных профессий приходится иметь дело с задачами на дробно-рациональные уравнения.

И на свете нет профессий
Вы заметьте-ка
Где бы нам не пригодилась Ма-те-ма-ти-ка!

3) Открытие новых знаний.

Итак, тема нашего урока «Рациональные уравнения как математические модели реальных ситуаций».

( Записать в тетради тему урока.)

— Где мы используем математические модели? (при решении задач)

— Назовите этапы решения задачи.

Проблемный вопрос. — Что необходимо сделать перед решением какой — нибудь задачи? (Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, понять какую величину обозначить за неизвестную).

— Работать сегодня мы будем в группах. Вспомните правила работы в группах. (Прислушиваться к мнению соседей, работать дружно, помогать друг другу)

Класс разбит на группы по 4-5 человек ( у нас в классе 16 учащихся- 3 группы, сидят по группам с начала урока). Учитель раздает карточки с заданием каждой группе, ставит задачу: составить уравнение к задачам и записать пояснения. Во время работы учитель контролирует выполнение заданий, отвечает на вопросы, при возникновении затруднений оказывает помощь учащимся.

После составления уравнений к задачам, они записываются на доску и в тетради.

4) Домашнее задание: решить составленные уравнения и дать ответ к задачам (учащиеся получают условия всех задач на дом).

5) Итог урока.

То интересна, то сложна.

Пусть вам будут по плечу любые задачи. Успехов! Спасибо за урок!

Видео:8 класс, 28 урок, Рациональные уравнения как математические модели реальных ситуацийСкачать

Конспект урока: « Рациональные уравнения как математические модели реальных ситуаций»
план-конспект урока по алгебре (8 класс) на тему

Цель урока: совершенствовать и систематизировать знания о математической модели, полученные обучающимися в 7 классе. В ходе урока ученики поделятся своими ассоциациями со словосочетанием «рациональное уравнение», вспомнят этапы решения задачи, научаться составлять математическую модель с помощью таблицы. Вся работа проходит в группах и носит конкурсный характер.

Видео:№ 804 - Алгебра 8 класс МерзлякСкачать

Скачать:

Видео:Рациональные уравнения как математические модели реальных ситуаций - алгебра 8 классСкачать

Предварительный просмотр:

« Рациональные уравнения как математические модели реальных ситуаций»

Алгебра. 8класс. В 2 частях. Ч. 1. Учебник для учащихся общеобразовательных учреждений/ А.Г. Мордкович. – М.: Мнемозина,

Алгебра. 8класс. В 2 ч. Ч. 2. Задачник для учащихся

общеобразовательных учреждений/ А.Г.Мордкович. – М.: Мнемозина,

Цель урока : совершенствовать и систематизировать знания о математической модели, полученные обучающимися в 7 классе.

— образовательные ( формирование познавательных УУД ) :

выделять величины и обозначать их буквами; формулировать зависимости между величинами; записывать в виде алгебраического выражения словесно сформулированную зависимость и обратно; составлять уравниваемые алгебраические выражения; выражать одну и ту же зависимость разными способами; интерпретировать результат решения уравнения на языке данной задачи;

— воспитательные ( формирование коммуникативных и личностных УУД ) :

прививать интерес к предмету путём решения задач, связанных с жизненной деятельностью человека; формировать навыки аккуратного и грамотного математического письма;

— развивающие ( формирование регулятивных УУД ):

развивать творческую и мыслительную деятельность учащихся на уроке через решение задач поискового характера: интеллектуальные качества личности ребёнка, такие как способность оценивать, обобщать; способствовать формированию навыков самостоятельной работы, культуры общения, культуры коллективного умственного труда, культуры ответа на вопрос.

Тип урока : комбинированный.

Формы работы учащихся: фронтальная, индивидуальная, групповая

Оборудование: учебники по математике, презентация, компьютер, проектор, доска

1. Организационный момент;
2. Определение темы урока
3. Актуализация опорных знаний;
4. Этап изучения нового материала;
5. Решение задач на закрепление пройденной темы;
6. Подведение итогов, рефлексия, д/з.

I. Организационный момент. Учитель приветствует учеников и гостей. Проверяет готовность к уроку. Делит на группы по 5-человек и объявляет урок групповой работы и девиз

“Если все вместе идут вперед, то успех позаботится о себе сам.” – слайд № 1

II. Определение темы урока. На предыдущих уроках мы научились решать рациональные уравнения. Ребята, для чего нам нужен данный навык? Как его можно применить на практике, в жизни? (Для решения задач, которые описывают реальные ситуации из жизни).

Как вы думаете, если мы научились решать рациональные уравнения, то следующий шаг, какой? (с помощью них решать задачи). На слайде № 2 выводится тема урока.

III. Актуализация опорных знаний

Учитель предлагает учащимся в группе записать слова ассоциации, когда им говорят «рациональное уравнение». Далее каждая группа говорит свою ассоциацию, объясняет её, учитель записывает на доске (дробь, числитель, знаменатель, общий знаменатель, дополнительный множитель, приведение подобных слагаемых, квадратное уравнение, дискриминант, корни уравнения, посторонний корень и т.д.).

На слайде № 3 выводится алгоритм решения рационального уравнения.

IV. Работа по теме урока, изучение новой темы.

— Ребята, мы с вами не впервые решаем задачи с помощью уравнений и знаем, что решение задачи делится на три этапа:

1. составление математической модели;

2.работа с составленной моделью;

3.ответ на вопрос задачи.

На слайде № 4 выводится три этапа решения задачи.

— А теперь давайте решим задачу. Предлагаю 1 этап «составление математической модели», выполнить в группах с помощью таблицы.

1 этап составление математической модели (слайд № 5).

Две бригады должны были изготовить по 180 книжных полок. Первая бригада в час изготовляла на 2 полки больше, чем вторая, и потому закончила работу на 3 часа раньше. За сколько часов каждая бригада выполнила задание?
Для решения данной задачи удобнее использовать таблицу (в классах, с сильными учениками, данного типа задачи оформляются с объяснениями).

Видео:Алгебра 8 класс : Рациональные уравнения как математические модели реальных ситуаций.Скачать

Презентация по алгебре на тему «Рациональные уравнения как математические модели реальных ситуаций» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Рациональные уравнения как математические модели реальных ситуаций.

Всякая хорошо решенная математическая задача доставляет умственное наслаждение. Г. Гессе

Повторение пройденного материала

Повторение пройденного материала

Повторение пройденного материала Алгоритм решения дробных рациональных уравнений. Найти область допустимых значений ОДЗ. Перенести все члены уравнения в левую часть. Привести все члены уравнения к общему знаменателю. Решить полученное целое уравнение. Исключить те корни, которые не удовлетворяют ОДЗ.

Понятие математической модели Представление реальной ситуации на языке математики с использованием различных правил, свойств и законов математики называется математической моделью задачи. Различают несколько видов математических моделей: алгебраическая модель; графическая модель; геометрическая модель.

Этапы решения задачи 1 этап. Составление математической модели. Вводится переменная, текст задачи переводится на математический язык, составляется уравнение. 2 этап. Работа с математической моделью. Решение уравнения. 3 этап. Ответ на вопрос задачи. Анализируя полученное решение, записывается ответ на вопрос задачи.

Задачи на движение Расстояние Скорость время S=v·t

400км 400км х км/ч (х+20)км/ч Составим уравнение — = 1 на час быстрее разность > Пусть х км/ч скорость товарного поезда Искомую величину обозначим за x Расстояние в 400 км скорый поезд прошел на час быстрее товарного. Какова скорость каждого поезда, если скорость товарного поезда на 20км/ч меньше скорого? Расстояние Скорость время Товарный поезд Скорый поезд Триггер – эффект исчезновение на зеленый прямоугольник

Мотоциклист проезжает расстояние 40 км на 1 час 20 мин быстрее велосипедиста. Найти скорость, мотоциклиста, если она на 40км/ч больше скорости велосипедиста. Составить уравнение к задаче, приняв за х скорость велосипедиста. 1час 20мин =? > Х км/ч Расстояние Скорость время Велосипедист 40км Хкм/ч мотоциклист 40км (х+40)км/ч Триггер картинка –исчезновение появление таблицы, потом по щелчку появление уравнения для проверки

Задачи на движение по течению и против течения реки Собственная скорость катера Vc Скорость течения реки Vт по течению Vc+Vт против течения Vc-Vт По течению

Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на 2 часа. После этого он прошел еще 27 км по течению реки и прибыл в пункт назначения в 19 часов. Найти собственную скорость катера , если скорость течения реки 2 км/час. Составить уравнение к задаче Искомую величину обозначим за x Расстояние Скорость время По течению 27 км (х+2)км/ч Против течения 7км (х-2)км/ч

Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на 2 часа. После этого он прошел еще 27 км по течению реки и прибыл в пункт назначения в 19 часов. Найти собственную скорость катера , если скорость течения реки 2 км/час. Составим уравнение Вычислим время движения катера

Краткое описание документа:

Рациональные уравнения как математические модели реальных ситуаций. Всякая хорошо решенная математическая задача доставляет умственное наслаждение. Г. Гессе Повторение пройденного материала Повторение пройденного материала Повторение пройденного материала Алгоритм решения дробных рациональных уравнений. Найти область допустимых значений ОДЗ. Перенести все члены уравнения в левую часть. Привести все члены уравнения к общему знаменателю. Решить полученное целое уравнение. Исключить те корни, которые не удовлетворяют ОДЗ. Понятие математической модели Представление реальной ситуации на языке математики с использованием различных правил, свойств и законов математики называется математической моделью задачи. Различают несколько видов математических моделей: алгебраическая модель; графическая модель; геометрическая модель. Этапы решения задачи 1 этап. Составление математической модели. Вводится переменная, текст задачи переводится на математический язык, составляется уравнение. 2 этап. Работа с математической моделью. Решение уравнения. 3 этап. Ответ на вопрос задачи. Анализируя полученное решение, записывается ответ на вопрос задачи. Задачи на движение Расстояние Скорость время S=v·t 400км 400км х км/ч (х+20)км/ч Составим уравнение — = 1 на час быстрее разность > Пусть х км/ч скорость товарного поезда Искомую величину обозначим за x Расстояние в 400 км скорый поезд прошел на час быстрее товарного. Какова скорость каждого поезда, если скорость товарного поезда на 20км/ч меньше скорого? Расстояние Скорость время Товарный поезд Скорый поезд Триггер – эффект исчезновение на зеленый прямоугольник Мотоциклист проезжает расстояние 40 км на 1 час 20 мин быстрее велосипедиста. Найти скорость, мотоциклиста, если она на 40км/ч больше скорости велосипедиста. Составить уравнение к задаче, приняв за х скорость велосипедиста. 1час 20мин =? > Х км/ч Расстояние Скорость время Велосипедист 40км Хкм/ч мотоциклист 40км (х+40)км/ч Триггер картинка –исчезновение появление таблицы, потом по щелчку появление уравнения для проверки Задачи на движение по течению и против течения реки Собственная скорость катера Vc Скорость течения реки Vт по течению Vc+Vт против течения Vc-Vт По течению Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на 2 часа. После этого он прошел еще 27 км по течению реки и прибыл в пункт назначения в 19 часов. Найти собственную скорость катера , если скорость течения реки 2 км/час. Составить уравнение к задаче Искомую величину обозначим за x Расстояние Скорость время По течению 27 км (х+2)км/ч Против течения 7км (х-2)км/ч Катер отправился в путь в 15 часов, прошел 7км против течения реки и сделал остановку на 2 часа. После этого он прошел еще 27 км по течению реки и прибыл в пункт назначения в 19 часов. Найти собственную скорость катера , если скорость течения реки 2 км/час. Составим уравнение Вычислим время движения катера

🌟 Видео

Рациональные уравнения как математические модели реальных ситуаций (урок 1)Скачать

Рациональные уравнения как математические модели реальных ситуаций (урок 2)Скачать

Рациональные уравнения как математические модели реальных ситуаций | Алгебра 8 класс #39 | ИнфоурокСкачать

Рациональные уравнения как модели реальных ситуаций. §24 алгебра 8 классСкачать

Рациональные уравнения как математические модели реальных ситуаций | Алгебра 8 класс #41 | ИнфоурокСкачать

Рациональные уравнения как математические модели реальных ситуацийСкачать

Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Рациональные уравнения как математические модели реальных ситуаций | Алгебра 8 класс #40 | ИнфоурокСкачать

Рациональные уравнения как математические модели реальных ситуаций | Алгебра 8 класс #38 | ИнфоурокСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

8 класс Рациональные уравнения как математические модели реальных ситуацийСкачать

Рациональные уравнения как математические модели реальных ситуаций 2 урокСкачать

МЕРЗЛЯК-8 РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. ПАРАГРАФ-7 ТЕОРИЯСкачать

8 класс "Рациональные уравнения как математические модели реальных ситуаций" (Часть 1)Скачать

Рациональные уравнения как математические модели реальных ситуаций 1 урокСкачать

Рациональные уравнения как математические модели реальных ситуаций.Скачать