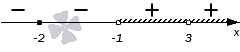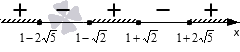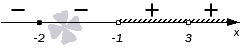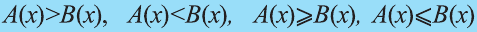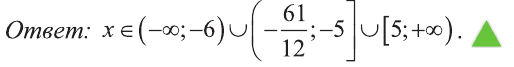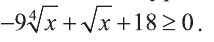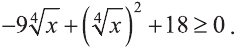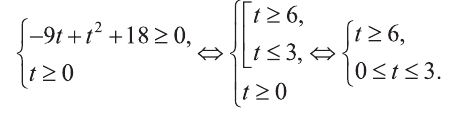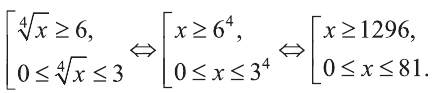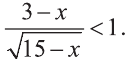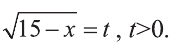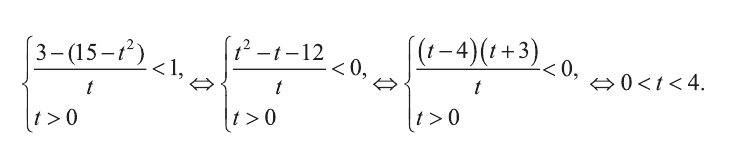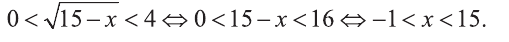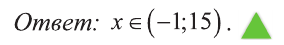Рациональные уравнения и неравенства что это

Видео:Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Решение целых и дробно рациональных неравенств

Продолжаем разбирать способы решения неравенств, имеющих в составе одну переменную. Мы уже изучили линейные и квадратные неравенства, которые представляют из себя частные случаи рациональных неравенств. В этой статье мы уточним, неравенства какого типа относятся к рациональным, расскажем, на какие виды они делятся (целые и дробные). После этого покажем, как правильно их решать, приведем нужные алгоритмы и разберем конкретные задачи.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Понятие рациональных равенств

Когда в школе изучают тему решения неравенств, то сразу берут рациональные неравенства. На них приобретаются и оттачиваются навыки работы с этим видом выражений. Сформулируем определение данного понятия:

Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обоих частях рациональные выражения.

Отметим, что определение никак не затрагивает вопрос количества переменных, значит, их может быть сколь угодно много. Следовательно, возможны рациональные неравенства с 1 , 2 , 3 и более переменными. Чаще всего приходится иметь дело с выражениями, содержащими всего одну переменную, реже две, а неравенства с большим количеством переменных обычно в рамках школьного курса не рассматривают вовсе.

Таким образом, мы можем узнать рациональное неравенство, посмотрев на его запись. И с правой, и с левой стороны у него должны быть расположены рациональные выражения. Приведем примеры:

x > 4 x 3 + 2 · y ≤ 5 · ( y − 1 ) · ( x 2 + 1 ) 2 · x x — 1 ≥ 1 + 1 1 + 3 x + 3 · x 2

А вот неравенство вида 5 + x + 1 x · y · z не относится к рациональным, поскольку слева у него есть переменная под знаком корня.

Все рациональные неравенства делятся на целые и дробные.

Целое рациональное равенство состоит из целых рациональных выражений (в обеих частях).

Дробно рациональное равенство – это такое равенство, которое содержит дробное выражение в одной или обеих своих частях.

Например, неравенства вида 1 + x — 1 1 3 2 2 + 2 3 + 2 11 — 2 · 1 3 · x — 1 > 4 — x 4 и 1 — 2 3 5 — y > 1 x 2 — y 2 являются дробно рациональными, а 0 , 5 · x ≤ 3 · ( 2 − 5 · y ) и 1 : x + 3 > 0 – целыми.

Мы разобрали, что из себя представляют рациональные неравенства, и выделили их основные типы. Можем переходить дальше, к обзору способов их решения.

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Как решать целые неравенства

Допустим, что нам требуется найти решения целого рационального неравенства r ( x ) s ( x ) , которое включает в себя только одну переменную x . При этом r ( x ) и s ( x ) представляют собой любые целые рациональные числа или выражения, а знак неравенства может отличаться. Чтобы решить это задание, нам нужно преобразовать его и получить равносильное равенство.

Начнем с перенесения выражения из правой части в левую. Получим следующее:

вида r ( x ) − s ( x ) 0 ( ≤ , > , ≥ )

Мы знаем, что r ( x ) − s ( x ) будет целым значением, а любое целое выражение допустимо преобразовать в многочлен. Преобразуем r ( x ) − s ( x ) в h ( x ) . Это выражение будет тождественно равным многочленом. Учитывая, что у r ( x ) − s ( x ) и h ( x ) область допустимых значений x одинакова, мы можем перейти к неравенствам h ( x ) 0 ( ≤ , > , ≥ ) , которое будет равносильно исходному.

Зачастую такого простого преобразования будет достаточно для решения неравенства, поскольку в итоге может получиться линейное или квадратное неравенство, значение которого вычислить несложно. Разберем такие задачи.

Условие: решите целое рациональное неравенство x · ( x + 3 ) + 2 · x ≤ ( x + 1 ) 2 + 1 .

Решение

Начнем с переноса выражения из правой части в левую с противоположным знаком.

x · ( x + 3 ) + 2 · x − ( x + 1 ) 2 − 1 ≤ 0

Теперь, когда мы выполнили все действия с многочленами слева, можно переходить к линейному неравенству 3 · x − 2 ≤ 0 , равносильному тому, что было дано в условии. Решить его несложно:

Ответ: x ≤ 2 3 .

Условие: найдите решение неравенства ( x 2 + 1 ) 2 − 3 · x 2 > ( x 2 − x ) · ( x 2 + x ) .

Решение

Переносим выражение из левой части в правую и выполняем дальнейшие преобразования с помощью формул сокращенного умножения.

( x 2 + 1 ) 2 − 3 · x 2 − ( x 2 − x ) · ( x 2 + x ) > 0 x 4 + 2 · x 2 + 1 − 3 · x 2 − x 4 + x 2 > 0 1 > 0

В итоге наших преобразований мы получили неравенство, которое будет верным при любых значениях x , следовательно, решением исходного неравенства может быть любое действительное число.

Ответ: любое действительно число.

Условие: решите неравенство x + 6 + 2 · x 3 − 2 · x · ( x 2 + x − 5 ) > 0 .

Решение

Из правой части мы ничего переносить не будем, поскольку там 0 . Начнем сразу с преобразования левой части в многочлен:

x + 6 + 2 · x 3 − 2 · x 3 − 2 · x 2 + 10 · x > 0 − 2 · x 2 + 11 · x + 6 > 0 .

Мы вывели квадратное неравенство, равносильное исходному, которое легко решить несколькими методами. Применим графический способ.

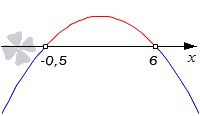
Начнем с вычисления корней квадратного трехчлена − 2 · x 2 + 11 · x + 6 :

D = 11 2 — 4 · ( — 2 ) · 6 = 169 x 1 = — 11 + 169 2 · — 2 , x 2 = — 11 — 169 2 · — 2 x 1 = — 0 , 5 , x 2 = 6

Теперь на схеме отметим все необходимые нули. Поскольку старший коэффициент меньше нуля, ветви параболы на графике будут смотреть вниз.

Нам будет нужна область параболы, расположенная над осью абсцисс, поскольку в неравенстве у нас стоит знак > . Нужный интервал равен ( − 0 , 5 , 6 ) , следовательно, эта область значений и будет нужным нам решением.

Ответ: ( − 0 , 5 , 6 ) .

Бывают и более сложные случаи, когда слева получается многочлен третьей или более высокой степени. Чтобы решить такое неравенство, рекомендуется использовать метод интервалов. Сначала мы вычисляем все корни многочлена h ( x ) , что чаще всего делается с помощью разложения многочлена на множители.

Условие: вычислите ( x 2 + 2 ) · ( x + 4 ) 14 − 9 · x .

Решение

Начнем, как всегда, с переноса выражения в левую часть, после чего нужно будет выполнить раскрытие скобок и приведение подобных слагаемых.

( x 2 + 2 ) · ( x + 4 ) − 14 + 9 · x 0 x 3 + 4 · x 2 + 2 · x + 8 − 14 + 9 · x 0 x 3 + 4 · x 2 + 11 · x − 6 0

В итоге преобразований у нас получилось равносильное исходному равенство, слева у которого стоит многочлен третьей степени. Применим метод интервалов для его решения.

Сначала вычисляем корни многочлена, для чего нам надо решить кубическое уравнение x 3 + 4 · x 2 + 11 · x − 6 = 0 . Имеет ли оно рациональные корни? Они могут быть лишь в числе делителей свободного члена, т.е. среди чисел ± 1 , ± 2 , ± 3 , ± 6 . Подставим их по очереди в исходное уравнение и выясним, что числа 1 , 2 и 3 будут его корнями.

Значит, многочлен x 3 + 4 · x 2 + 11 · x − 6 может быть описан в виде произведения ( x − 1 ) · ( x − 2 ) · ( x − 3 ) , и неравенство x 3 + 4 · x 2 + 11 · x − 6 0 может быть представлено как ( x − 1 ) · ( x − 2 ) · ( x − 3 ) 0 . С неравенством такого вида нам потом будет легче определить знаки на промежутках.

Далее выполняем оставшиеся шаги интервального метода: рисуем числовую прямую и точки на ней с координатами 1 , 2 , 3 . Они разбивают прямую на 4 промежутка, в которых нужно определить знаки. Заштрихуем промежутки с минусом, поскольку исходное неравенство имеет знак .

Нам осталось только записать готовый ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .

Ответ: ( − ∞ , 1 ) ∪ ( 2 , 3 ) .

В некоторых случаях выполнять переход от неравенства r ( x ) − s ( x ) 0 ( ≤ , > , ≥ ) к h ( x ) 0 ( ≤ , > , ≥ ) , где h ( x ) – многочлен в степени выше 2 , нецелесообразно. Это распространяется на те случаи, когда представить r ( x ) − s ( x ) как произведение линейных двучленов и квадратных трехчленов проще, чем разложить h ( x ) на отдельные множители. Разберем такую задачу.

Условие: найдите решение неравенства ( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) ≥ 2 · x · ( x 2 − 2 · x − 1 ) .

Решение

Данное неравенство относится к целым. Если мы перенесем выражение из правой части влево, раскроем скобки и выполним приведение слагаемых, то получим x 4 − 4 · x 3 − 16 · x 2 + 40 · x + 19 ≥ 0 .

Решить такое неравенство непросто, поскольку придется искать корни многочлена четвертой степени. Оно не имеет ни одного рационального корня (так, 1 , − 1 , 19 или − 19 не подходят), а искать другие корни сложно. Значит, воспользоваться этим способом мы не можем.

Но есть и другие способы решения. Если мы перенесем выражения из правой части исходного неравенства в левую, то сможем выполнить вынесение за скобки общего множителя x 2 − 2 · x − 1:

( x 2 − 2 · x − 1 ) · ( x 2 − 19 ) − 2 · x · ( x 2 − 2 · x − 1 ) ≥ 0 ( x 2 − 2 · x − 1 ) · ( x 2 − 2 · x − 19 ) ≥ 0 .

Мы получили неравенство, равносильное исходному, и его решение даст нам искомый ответ. Найдем нули выражения в левой части, для чего решим квадратные уравнения x 2 − 2 · x − 1 = 0 и x 2 − 2 · x − 19 = 0 . Их корни – 1 ± 2 , 1 ± 2 5 . Переходим к равенству x — 1 + 2 · x — 1 — 2 · x — 1 + 2 5 · x — 1 — 2 5 ≥ 0 , которое можно решить методом интервалов:

Согласно рисунку, ответом будет — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Ответ: — ∞ , 1 — 2 5 ∪ 1 — 2 5 , 1 + 2 ∪ 1 + 2 5 , + ∞ .

Добавим, что иногда нет возможности найти все корни многочлена h ( x ) , следовательно, мы не можем представить его в виде произведения линейных двучленов и квадратных трехчленов. Тогда решить неравенство вида h ( x ) 0 ( ≤ , > , ≥ ) мы не можем, значит, решить исходное рациональное неравенство тоже нельзя.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Как решать дробно рациональные неравенства

Допустим, надо решить дробно рационально неравенств вида r ( x ) s ( x ) ( ≤ , > , ≥ ) , где r ( x ) и s ( x ) являются рациональными выражениями, x – переменной. Хотя бы одно из указанных выражений будет дробным. Алгоритм решения в этом случае будет таким:

1. Определяем область допустимых значений переменной x .
2. Переносим выражение из правой части неравенства налево, а получившееся выражение r ( x ) − s ( x ) представляем в виде дроби. При этом где p ( x ) и q ( x ) будут целыми выражениями, которые являются произведениями линейных двучленов, неразложимых квадратных трехчленов, а также степеней с натуральным показателем.
3. Далее решаем полученное неравенство методом интервалов.
4. Последним шагом является исключение точек, полученных в ходе решения, из области допустимых значений переменной x , которую мы определили в начале.

Это и есть алгоритм решения дробно рационального неравенства. Большая часть его понятна, небольшие пояснения требуются только для п. 2 . Мы перенесли выражение из правой части налево и получили r ( x ) − s ( x ) 0 ( ≤ , > , ≥ ) , а как потом привести его к виду p ( x ) q ( x ) 0 ( ≤ , > , ≥ ) ?

Сначала определим, всегда ли можно выполнить данное преобразование. Теоретически, такая возможность имеется всегда, поскольку в рациональную дробь можно преобразовать любое рациональное выражение. Здесь же у нас есть дробь с многочленами в числителе и знаменателе. Вспомним основную теорему алгебры и теорему Безу и определим, что любой многочлен n -ной степени, содержащий одну переменную, может быть преобразован в произведение линейных двучленов. Следовательно, в теории мы всегда можем преобразовать выражение таким образом.

На практике разложение многочленов на множители зачастую оказывается довольно трудной задачей, особенно если степень выше 4 . Если мы не сможем выполнить разложение, то не сможем и решить данное неравенство, однако в рамках школьного курса такие проблемы обычно не изучаются.

Далее нам надо решить, будет ли полученное неравенство p ( x ) q ( x ) 0 ( ≤ , > , ≥ ) равносильным по отношению к r ( x ) − s ( x ) 0 ( ≤ , > , ≥ ) и к исходному. Есть вероятность, что оно может оказаться и неравносильным.

Равносильность неравенства будет обеспечена тогда, когда область допустимых значений p ( x ) q ( x ) совпадет с областью значений выражения r ( x ) − s ( x ) . Тогда последний пункт инструкции по решению дробно рациональных неравенств выполнять не нужно.

Но область значений для p ( x ) q ( x ) может оказаться шире, чем у r ( x ) − s ( x ) , например, за счет сокращения дробей. Примером может быть переход от x · x — 1 3 x — 1 2 · x + 3 к x · x — 1 x + 3 . Либо это может происходить при приведении подобных слагаемых, например, здесь:

x + 5 x — 2 2 · x — x + 5 x — 2 2 · x + 1 x + 3 к 1 x + 3

Для таких случаев и добавлен последний шаг алгоритма. Выполнив его, вы избавитесь от посторонних значений переменной, которые возникают из-за расширения области допустимых значений. Возьмем несколько примеров, чтобы было более понятно, о чем идет речь.

Условие: найдите решения рационального равенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x x — 3 2 · x + 1 .

Решение

Действуем по алгоритму, указанному выше. Сначала определяем область допустимых значений. В данном случае она определяется системой неравенств x + 1 · x — 3 ≠ 0 x — 3 2 ≠ 0 x — 3 2 · ( x + 1 ) ≠ 0 , решением которой будет множество ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .

Далее нам надо сделать так, чтобы в правой части неравенства получился 0 . Выполняем перенос выражения из правой части влево с противоположным знаком и получаем неравенство, равносильное исходному:

x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) ≥ 0

После этого нам нужно преобразовать его так, чтобы было удобно применить метод интервалов. Первым делом приводим алгебраические дроби к наименьшему общему знаменателю ( x − 3 ) 2 · ( x + 1 ) :

x x + 1 · x — 3 + 4 ( x — 3 ) 2 + 3 · x ( x — 3 ) 2 · ( x + 1 ) = = x · x — 3 + 4 · x + 1 + 3 · x x — 3 2 · x + 1 = x 2 + 4 · x + 4 ( x — 3 ) 2 · ( x + 1 )

Сворачиваем выражение в числителе, применяя формулу квадрата суммы:

x 2 + 4 · x + 4 x — 3 2 · x + 1 = x + 2 2 x — 3 2 · x + 1

Областью допустимых значений получившегося выражения является ( − ∞ , − 1 ) ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) . Мы видим, что она аналогична той, что была определена для исходного равенства. Заключаем, что неравенство x + 2 2 x — 3 2 · x + 1 ≥ 0 является равносильным исходному, значит, последний шаг алгоритма нам не нужен.

Используем метод интервалов:

Видим решение ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) , которое и будет решением исходного рационального неравенства x x + 1 · x — 3 + 4 x — 3 2 ≥ — 3 · x ( x — 3 ) 2 · ( x + 1 ) .

Ответ: ∪ ( − 1 , 3 ) ∪ ( 3 , + ∞ ) .

Условие: вычислите решение x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 .

Решение

Определяем область допустимых значений. В случае с этим неравенством она будет равна всем действительным числам, кроме − 2 , − 1 , 0 и 1 .

Переносим выражения из правой части в левую:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 > 0

Далее выполняем преобразование левой части. Сначала преобразуем первую дробь:

x + 3 x — 1 — 3 x x + 2 = x + 3 — x — 3 x x + 2 = 0 x x + 2 = 0 x + 2 = 0

Учитывая получившийся результат, запишем:

x + 3 x — 1 — 3 x x + 2 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 0 + 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 x 2 — 1 = = 2 x — 1 — 1 x + 1 — 2 · x + 2 ( x + 1 ) · x — 1 = = — x — 1 ( x + 1 ) · x — 1 = — x + 1 ( x + 1 ) · x — 1 = — 1 x — 1

Для выражения — 1 x — 1 областью допустимых значений будет множество всех действительных чисел, за исключением единицы. Мы видим, что область значений расширилась: в нее были добавлены − 2 , − 1 и 0 . Значит, нам нужно выполнить последний шаг алгоритма.

Поскольку мы пришли к неравенству — 1 x — 1 > 0 , можем записать равносильное ему 1 x — 1 0 . С помощью метода интервалов вычислим решение и получим ( − ∞ , 1 ) .

Исключаем точки, которые не входят в область допустимых значений исходного равенства. Нам надо исключить из ( − ∞ , 1 ) числа − 2 , − 1 и 0 . Таким образом, решением рационального неравенства x + 3 x — 1 — 3 x x + 2 + 2 x — 1 > 1 x + 1 + 2 · x + 2 x 2 — 1 будут значения ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .

Ответ: ( − ∞ , − 2 ) ∪ ( − 2 , − 1 ) ∪ ( − 1 , 0 ) ∪ ( 0 , 1 ) .

В заключение приведем еще один пример задачи, в котором окончательный ответ зависит от области допустимых значений.

Условие: найдите решение неравенства 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 .

Решение

Область допустимых значений неравенства, заданного в условии, определяет система x 2 ≠ 0 x 2 — x + 1 ≠ 0 x — 1 ≠ 0 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≠ 0 .

Решений у этой системы нет, поскольку

x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 = = ( x + 1 ) · x 2 — x + 1 x 2 — x + 1 — ( x — 1 ) · x + 1 x — 1 = = x + 1 — ( x + 1 ) = 0

Значит, исходное равенство 5 + 3 x 2 x 3 + 1 x 2 — x + 1 — x 2 — 1 x — 1 ≥ 0 не имеет решения, поскольку нет таких значений переменной, при которой оно имело бы смысл.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Рациональные неравенства

Рациональное неравенство — это неравенство, которое можно свести к виду [Large<dfrac

lor 0>] где (P(x), Q(x)) — многочлены.
( (lor) — один из знаков (geqslant, leqslant, >, )
Например, следующие неравенства являются рациональными: [dfrac1>0,qquad x+2+dfrac

[<Large<text>>] Линейные неравенства – это неравенства вида [ax+b lor 0, qquad lor — text geqslant, leqslant, >, или сводящиеся к такому виду.
Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа ( (xin mathbb) ).

Общее правило решения линейных неравенств:

1) Для того, чтобы решить данное неравенство, необходимо привести его к виду (axlor -b) , то есть перенести число (b) в правую часть.

2) Если коэффициент (a) перед (x) – положительный, то неравенство равносильно (xlor -dfrac ba) , то есть после деления обеих частей неравенства на (a) знак неравенства не меняется.

3) Если коэффициент (a) перед (x) – отрицательный, то неравенство равносильно (xland -dfrac ba) , то есть после деления обеих частей неравенства на (a) знак неравенства меняется на противоположный.

4) Если (a=0) , то неравенство равносильно (0lor -b) , что либо верно при всех значениях переменной (x) (например, если это (0>-1) ), либо неверно ни при каких значениях (x) (например, если это (0leqslant -3) ).
То есть ответом будут либо (xinmathbb) , либо (xin varnothing) .

Замечание
Заметим, что знаку (leqslant) противоположен знак (geqslant) , а знаку ( – знак (>) . И наоборот.

Пример 1
Решить неравенство (5-3x>-1) .

Решение. I способ
Сделаем цепочку преобразований:

[5-3x>-1 Rightarrow -3x>-1-5 Rightarrow -3x>-6 Rightarrow x Таким образом, ответом будет (xin(-infty;2)) .
Заметим, что т.к. мы делили неравенство на (-3) , то знак неравенства поменялся.

Решение. II способ
Можно перенести слагаемое (-3x) в правую часть, а (-1) – в левую:

[5-3x>-1 Rightarrow 5+1>3x Rightarrow 3x

Пример 2
Решить неравенство ((1-sqrt2)x+2leqslant 0) .

Решение
Заметим, что перед (x) находится отрицательный коэффициент. Поэтому:

[(1-sqrt2)xleqslant -2 Rightarrow xgeqslant -dfrac 2] Преобразуем число (-dfrac 2) : домножим числитель и знаменатель дроби на сопряженное к (1-sqrt2) , то есть на (1+sqrt2) , чтобы избавиться от иррациональности в знаменателе:

[-dfrac 2=-dfrac= -dfrac=2(1+sqrt2)]
Таким образом, ответ (xin [2+2sqrt2;+infty)) .
Перейдем к квадратичным неравенствам, которые являются очень важным инструментом в решении задач.

Приступим к рассмотрению общего метода для решения любого рационального неравенства, то есть неравенства вида

Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа, кроме нулей знаменателя.

Существует два способа решения таких неравенств:

1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство ((*)) равносильно совокупности: [ <large<left[beginbegin &begin P(x)geqslant 0\ Q(x)>0 end\ &begin P(x)leqslant 0\ Q(x)

Такой способ подойдет для решения любого неравенства, где слева стоит дробь, а справа — (0) .
Но, как правило, для решения большинства рациональных неравенств он неудобен. Почему? Вы сможете убедиться в этом после того, как мы рассмотрим метод интервалов.

2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере конкретного неравенства, чтобы было понятней).
Заметим, что первые три шага созданы для того, чтобы преобразовать неравенство к более простому виду, что поможет вам не допустить ошибку в решении подобных задач. Метод интервалов – это всего лишь удобный инструмент для решения рациональных неравенств, и если вы будете всегда пользоваться одним и тем же алгоритмом, то вероятность допустить ошибку при решении таких неравенств будет минимальной.
Данный алгоритм специально расписан подробно, чтобы у вас не возникло вопросов; всего после нескольких использований этого алгоритма вы будете решать рациональные неравенства очень быстро и без ошибок!

1 ШАГ. Необходимо перенести все слагаемые в одну часть (пусть это будет левая часть) неравенства так, чтобы в другой части неравенства остался (0) , и привести эти слагаемые к общему знаменателю так, чтобы в левой части неравенства получилась дробь. Затем нужно разложить числитель и знаменатель полученной дроби, то есть многочлены (P(x), Q(x)) , на множители. Например, неравенство (dfrac1 нужно переписать в виде (dfrac1-1 , затем привести к общему знаменателю (dfrac1-dfrac , затем записать в виде одной дроби левую часть: (dfrac и привести подобные слагаемые: (dfrac .

Итак, пусть после разложения на множители неравенство приняло вид [dfrac geqslant0]

Заметим, что любой многочлен можно (а в нашем способе НУЖНО) разложить до произведения только линейных скобок ( (ax+b) ) и квадратичных скобок с отрицательным дискриминантом ((ax^2+bx+c), D .

2 ШАГ. Рассмотрим скобки, в которых остался квадратичный трехчлен с (D .

(bullet) Если при (x^2) находится положительный коэффициент (a>0) , то при всех значениях (x) выражение (ax^2+bx+c) положительно (не может быть равно нулю!). Т.к. мы имеем право делить неравенство на любое число/выражение, не равное (0) , то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является ((2x^2+3x+5)) ). Причем заметим, что т.к. мы делим на положительное выражение, то знак неравенства не меняется!

(bullet) Если при (x^2) находится отрицательный коэффициент (a , то при всех значениях (x) выражение (ax^2+bx+c) отрицательно. Т.к. мы имеем право делить неравенство на любое число/выражение, не равное (0) , то разделим обе части неравенства на такие скобки (в нашем неравенстве такой скобкой является ((2x-x^2-3)) ). Причем заметим, что т.к. мы делим на отрицательное выражение, то знак неравенства должен измениться на противоположный!

Итак, обобщим 2 шаг: квадратичные скобки с отрицательным дискриминантом можно просто вычеркнуть, причем при вычеркивании скобок с (a>0) знак неравенства остается прежним, а вот при вычеркивании скобок с (a знак неравенства меняется на противоположный столько раз, сколько было таких скобок. Лучше вычеркивать их последовательно по одной, каждый раз меняя знак неравенства на противоположный.

Таким образом, неравенство примет вид [dfrac leqslant 0]

3 ШАГ. Рассмотрим линейные скобки ((ax+b)) .

Назовем скобку хорошей, если при (x) находится положительный коэффициент (такие скобки мы трогать не будем), и плохой, если при (x) находится отрицательный коэффициент (в таких скобках необходимо поменять все знаки на противоположные, то есть сделать их хорошими).

Для того, чтобы в одной плохой скобке поменять все знаки на противоположные, необходимо домножить правую и левую части неравенства на (-1) . Таким образом, после одного такого действия знак неравенства сменится на противоположный. Значит, если плохих скобок четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.

Заметим, что выражение ((ax+b)^n) — это не что иное, как произведение (n) скобок ((ax+b)) .

В нашем неравенстве среди плохих одна скобка ((3-x)) и две скобки ((2-3x)) (т.к. ((2-3x)^2=(2-3x)(2-3x)) ), то есть всего три плохих скобки, следовательно, знак неравенства изменится и неравенство примет вид: [dfrac geqslant0quad (***)]

Заметим, что множитель (x^2) — это скобка ((x-0)^2) , или, что то же самое, ((x-0)(x-0)) – произведение двух одинаковых линейных скобок.

4 ШАГ. Теперь, когда левая часть неравенства состоит из произведения только хороших линейных скобок (в каких-то степенях), можно приступить к самому методу интервалов.

Его суть состоит в том, что левая часть неравенства — всюду непрерывная функция, кроме тех точек, где знаменатель дроби равен нулю. Поэтому точки, в которых эта функция равна нулю (то есть ее числитель равен нулю) и точки, в которых эта функция не существует (то есть ее знаменатель равен нулю), разбивают область определения этой функции на промежутки, причем на каждом промежутке функция принимает значения строго одного знака.

А нам как раз нужно найти те значения (x) , при которых функция (geqslant 0) . Причем, т.к. наша функция — рациональная, то ее область определения — это все действительные числа ( (mathbb) ), кроме нулей знаменателя. Поэтому отметим нули каждой скобки на вещественной прямой (а ноль каждой скобки – это как раз ноль числителя или знаменателя), причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как в примере, то есть (geqslant ) или (leqslant ) ) или выколотые (если знак неравенства строгий, то есть (>) или ( ).
Заметим, что если мы отметили (n) точек, то числовая прямая разобьется на (n+1) промежутков.

Расставим знак на каждом промежутке (color<<Large<text>>>) . Будем ставить “ (+) ”, если функция на этом промежутке принимает положительные значения, и “ (-) ” — если отрицательные. Нулю функция равна в закрашенных точках.
Первые три шага мы делали для того, чтобы не подставлять точки из каждого промежутка и не вычислять, какого знака будет левая часть неравенства (что бывает неудобно, если числа, которые нужно отмечать на прямой, “некрасивые”). Знаки мы будем расставлять, выявив некоторую закономерность. Какую – вы узнаете дальше.
Но в любом случае способ расстановки знаков путем подстановки чисел остается в нашем арсенале.

Т.к. все скобки – хорошие, то первый знак всегда будет “ (+,) ” (именно для этого мы и приводили неравенство к такому виду!). Действительно, если подставить любое число, превышающее самый большой корень (у нас самый большой корень (x=3) ), то каждая скобка будет положительна, значит, и произведение таких скобок будет всегда положительно.

Если какой-то корень входит в четное количество скобок, то при переходе через него (справа налево!) знак меняться не будет. В нашем неравенстве это точки (-1, 0, dfrac23) (например, точка (-1) входит в четное количество скобок: одна в числителе ((x+1)) и три в знаменателе ((x+1)^3) ).

Если точка входит в нечетное количество скобок, то при переходе через эту точку (справа налево!) знак будет меняться (в нашем неравенстве это точки (3) и (1) ).

5 ШАГ. Неравенство практически решено и нам остается только записать ответ. В нашем случае, т.к. знак преобразованного ((***)) неравенства (geqslant 0) (нестрогий), то в ответ пойдут промежутки со знаком “ (+,) ” (где значение функции больше нуля) и закрашенные точки (где значение функции равно нулю): [xin Big(-infty;-1Big)cup left(-1;dfrac23right)cup left(dfrac23;1right]cupBig(3;+inftyBig)] Напоминаем, что если точка не входит в ответ, то она пишется в круглой скобке “ (() ” или “ ()) ”, если входит в ответ – то в квадратной скобке “ ([) ” или “ (]) ”. Бесконечности всегда пишутся в круглых скобках.

Квадратичным неравенством называется любое неравенство вида [ax^2+bx+c lor 0, quad ane 0,]

или сводящееся к такому виду.

Область допустимых значений (x) (ОДЗ) таких неравенств — все вещественные числа ( (xin mathbb) ).

Квадратичные неравенства – это те же самые рациональные неравенства, следовательно, их также можно решать с помощью метода интервалов. Но давайте рассмотрим еще один способ, при помощи которого, как правило, удобнее решать квадратичные неравенства. Для этого нам понадобится вспомнить про параболу.

Замечание

Вспомним, как преобразуется квадратичный трехчлен (ax^2+bx+c) в зависимости от того, сколько корней он имеет.
Если квадратное уравнение (ax^2+bx+c=0)

(bullet) имеет два корня (x_1) и (x_2) (дискриминант (D>0) ), то (ax^2+bx+c=a(x-x_1)(x-x_2)) .

(bullet) имеет один корень (x_1) ( (D=0) ), то (ax^2+bx+c=a(x-x_1)^2) .

(bullet) не имеет корней ( (D ), то квадратный трехчлен (ax^2+bc+c) никогда не может быть равен нулю и не разлагается на линейные множители.

Шаг 1. Рассмотрим функцию (f(x)=ax^2+bx+c) . Графиком такой функции является парабола.
Для того, чтобы решить квадратичное неравенство, изобразим схематично параболу: то есть определим, куда направлены ее ветви и в каких точках она пересекает ось (Ox) .

Если (a>0) , то ветви направлены вверх, если (a , то ветви направлены вниз. Корни уравнения (ax^2+bx+c=0 (*)) и есть абсциссы точек, в которых парабола пересекает ось (Ox) .

Шаг 2. Таким образом, наша парабола будет одного из 6 видов: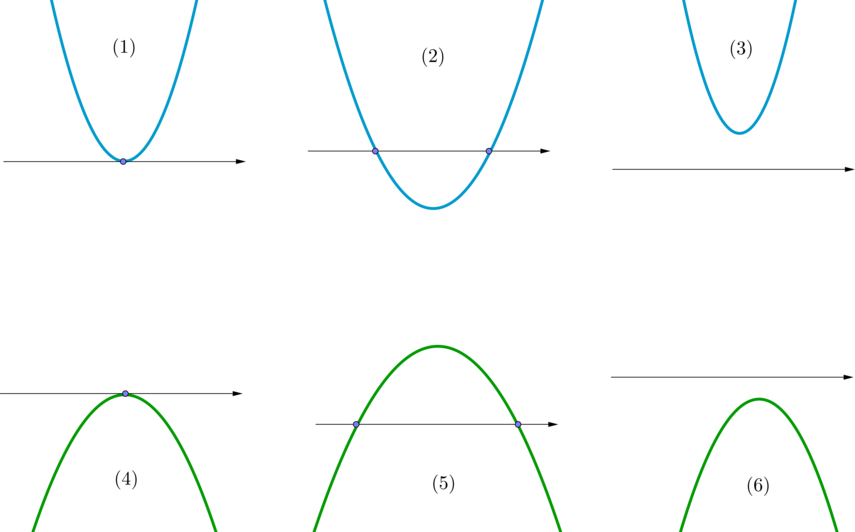
((1)) и ((4)) — когда уравнение ((*)) имеет один корень;
((2)) и ((5)) — когда уравнение ((*)) имеет два корня;
((3)) и ((6)) — когда уравнение ((*)) не имеет корней.

Часть параболы, находящая выше оси (Ox) , отвечает за (f(x)>0) ;
часть параболы, находящаяся ниже оси (Ox) , отвечает за (f(x) ;
точки, в которых парабола пересекает ось (Ox) , отвечают за (f(x)=0) .

Пример 1.
Решить неравенство (x^2+3x+2geqslant 0) .

Решение
Решим уравнение (x^2+3x+2=0 Leftrightarrow x_1=-2, x_2=-1) . Таким образом, неравенство можно переписать в виде: ((x+1)(x+2)geqslant 0) . Ветви параболы направлены вверх, следовательно, схематично она выглядит как ((2)) . Т.к. знак неравенства (geqslant) , то решением неравенства будут те значения (x) , для которых график находится выше оси (Ox) , а именно (xin (-infty;-2]cup[-1;+infty)) .

Заметим, что точки (-2, -1) входят в ответ, потому что знак “больше или равно”.

Пример 2.
Решить неравенство (11x-3x^2-6>0)

Решение
Решим уравнение (11x-3x^2-6=0 quadLeftrightarrowquad x_1=dfrac23, x_2=3) . Таким образом, неравенство можно переписать в виде: (-3(x-3)(x-frac23)>0) .

1 способ. Ветви параболы направлены вниз, следовательно, схематично она выглядит как ((5)) . Т.к. знак неравенства (>) , то решением неравенства будут (xin left(dfrac23;3right)) .

2 способ. Домножим правую и левую части неравенства на (-1) , получим (3(x-3)(x-frac23) (заметим, что знак сменился на противоположный). У новой параболы (Big(f(x)=3(x-3)(x-frac23)Big)) ветви направлены вверх, следовательно, схематично она выглядит как ((2)) . Но знак неравенства уже ( . Решением нового неравенства, естественно, будут те же (xin left(dfrac23;3right)) .

Таким образом, если в квадратичном неравенстве отрицательный знак при (x^2) , то можно сначала домножить неравенство на (-1) (и не забыть поменять знак неравенства), чтобы ветви параболы всегда были направлены вверх.

Пример 3.
Решить неравенство (x^2+4x+4 geqslant 0) .

Решение
Вспомнив формулу сокращенного умножения, получаем ((x+2)^2geqslant 0) (это быстрее, чем находить корни через дискриминант :)). Таким образом, парабола пересекает ось (Ox) в единственной точке (x_1=-2) и выглядит как ((1)) . А т.к. нам нужны те (x) , для которых график находится не ниже оси (Ox) , то решением неравенства будут (xin mathbb) , то есть выражение ((x+2)^2) всегда больше или равно (0) .

Как правило, подготовка школьников из Москвы (как и из других городов) к ЕГЭ начинается с повторения, а для кого-то и с изучения теории, например, по теме «Рациональные неравенства». Знакомство учащихся с данным разделом математики происходит в 9 классе, поэтому ничуть не удивительно, что у выпускников возникает потребность освежить в памяти правила. Если вы готовитесь к ЕГЭ, рациональные неравенства (теория) непременно стоит повторить. Сделать это вы можете, воспользовавшись нашим порталом.

«Школково» предлагает вам справочный материал, составленный нашими специалистами на основе собственного многолетнего опыта. Для того чтобы учащийся из Москвы или другого населенного пункта России, посетивший наш ресурс, смог легко и качественно подготовиться к ЕГЭ, мы в доступной форме изложили теорию по теме «Рациональные неравенства» и подобрали к ней интересные примеры с подробным описанием хода решения. После того как вы освоите материал, мы предлагаем вам закрепить его на практике. Прорешайте задания по теме, выбрав их в разделе «Каталог».

Видео:✓ Метод интервалов. Рациональные уравнения и неравенства | Борис ТрушинСкачать

Рациональные неравенства и их системы с примерами решения

Содержание:

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Простые рациональные неравенства и их системы

Рациональные неравенства одной переменной и методы их решения

Пусть А(х) и В(х) — рациональные выражения. Отношения вида

Пример:

Решите неравенство: 2(2х-5)(Зх-8)(5-4х) 0, то мы можем возвести обе части заданного неравенства в квадрат: При заданное неравенства обязательно выполняется:

Замена переменной

Этот метод аналогичен соответствующему методу замены переменной, использованному при решении иррациональных уравнений.

Пример:

Решите неравенство:

Решение:

Выпишем неравенство в виде:

Введем новую переменную: 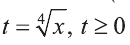В этом случае

Значит:

Пример:

Решите неравенство:

Решение:

Введем новую переменную:

Отсюда, 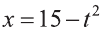и получим рациональное неравенство от переменной t:

Из последнего неравенства найдем х:

• Геометрические задачи и методы их решения
• Прямые и плоскости в пространстве
• Интеграл и его применение
• Первообразная и интегра
• Перпендикулярность в пространстве
• Векторы и координаты в пространстве
• Множества
• Рациональные уравнения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎦 Видео

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

решение УРАВНЕНИЙ решение НЕРАВЕНСТВ 10 11 классСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Рациональные неравенства. 8 класс.Скачать

ЛУЧШАЯ СТРАТЕГИЯ решения Целых Рациональных Уравнений (математика с нуля)Скачать

Решение неравенства методом интерваловСкачать

Равносильные уравнения. Рациональные уравнения - 8 класс алгебраСкачать

Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать