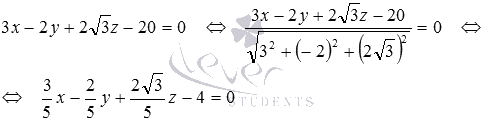Расстояние между плоскостями заданными уравнениями

Видео:Расстояние между параллельными прямымиСкачать

Формула для вычисления расстояния между плоскостями

Если заданы уравнения параллельных плоскостей A x + B y + C z + D₁ = 0 и A x + B y + C z + D₂ = 0, то расстояние между плоскостями можно найти, используя следующую формулу

Видео:Расстояние между плоскостямиСкачать

Примеры задач на вычисление расстояния между плоскостями

Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2

2 x + 4 y — 4 z + 18 = 0

Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:

Ответ: расстояние между плоскостями равно 4.

Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Расстояние между плоскостями. Онлайн калькулятор

Страница обновляется. Могут возникнуть ошибки. Спасибо за понимание!

С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Расстояние между плоскостями − теория

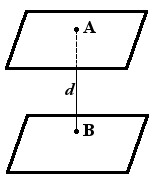
Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.

Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:

1. Проверка коллинеарности нормальных векторов плоскостей.
2. Нахождение некоторой точки M₀ на первой плоскости.
3. Вычисление расстояния между точкой M₀ и второй плоскостью.

Выведем формулу вычисления расстояния между плоскостями.

Запишем уравнения двух плоскостей:

Очевидно, что нормальные векторы n₁ и n₂ не могут быть нулевыми векторами.Если из пары коэффициентов (A₁,A₂),(B₁,B₂), (C₁,C₂) один нулевой а другой − нет, то нормальные векторы n₁ и n₂ неколлинеарны. Т.е. задача неразрешима.

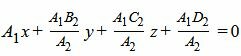(2′)

Нормальный вектор уравнения (2′) имеет следующий вид:

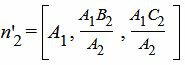Для коллинеарности векторов n₁ и n’₂(или n₁ и n₂) необходимо и достаточно выполнение следующих равенств:

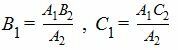(3)

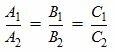(3′)

Если удовлетворяется условие (3) (или (3′)), то векторы n₁ и n’₂(или n₁ и n₂) коллинеарны, т.е. плоскости (1) и (2′) (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2′) можно представить так:

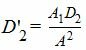2. Найдем некоторую точку на плоскости (1).

Легко убедится, что точка

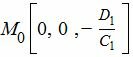(4)

принадлежит плоскости (1):

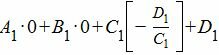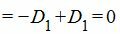3. Расстояние от точки M₀(x₀, y₀, z₀) до плоскости (2») вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):

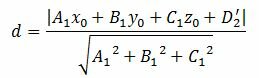(5)

Подставляя координаты точки M₀ из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2») (или (1) и (2)):

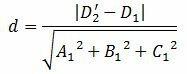(6)

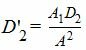Видео:Найти угол между плоскостямиСкачать

Расстояние между плоскостями − примеры и решения

Пример 1. Найти расстояние между плоскостями

(7)

(8)

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.

(8′)

Общее уравнение плоскости имеет вид:

где n=(A,B,C)− называется нормальным вектором плоскости.

Нормальный вектор плоскости (7) равен n₁=(1, 2, −4), нормальный вектор плоскости (8′) равен n₂=(1, 2, −4). n₁=n₂. Следовательно эти плоскости параллельны.

Найдем расстояние между плоскостями (7) и (8′), используя следующую формулу:

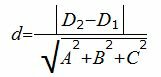(9)

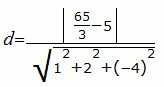Упростим и решим:

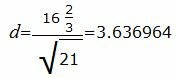Ответ. Расстояние между плоскостями равен:

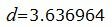Пример 2. Найти расстояние между плоскостями

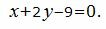(10)

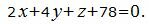(11)

Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.

Пример 3. Найти расстояние между плоскостями

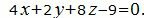(12)

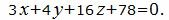(13)

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.

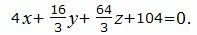(13′)

Нормальный вектор плоскости (12) равен n₁=(4, 2, 8), нормальный вектор плоскости (13′) равен n₂=(4, 16/3, 64/3). n₁≠n₂. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние между двумя параллельными плоскостями – определение и примеры нахождения.

В этой статье содержится ответ на вопрос: «Как найти расстояние между двумя параллельными плоскостями методом координат»? Сначала дано определение расстояния между параллельными плоскостями. Далее получена формула, позволяющая вычислять расстояние между параллельными плоскостями, которые заданы в прямоугольной системе координат. В заключении разобраны решения примеров и задач на нахождение расстояния между параллельными плоскостями.

Навигация по странице.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Расстояние между двумя параллельными плоскостями – определение.

Расстояние между двумя параллельными плоскостями определяется через расстояние от точки до плоскости. Покажем, как это делается.

Рассмотрим две параллельные плоскости и . Возьмем на любой из этих плоскостей точку М₁ и опустим перпендикуляр М₁H₁ из этой точки на другую плоскость. Длина перпендикуляра M₁H₁ является расстоянием между параллельными плоскостями и .

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Такое определение расстояния между параллельными плоскостями не случайно. Оно тесно связано со следующей теоремой.

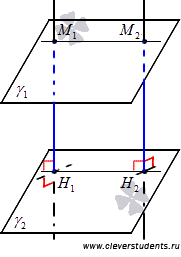
Все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости.

Пусть нам даны две параллельные плоскости и . Чтобы доказать эту теорему нам нужно доказать, что два перпендикуляра М₁H₁ и M₂H₂ , проведенные из различных точек М₁ и М₂ одной из заданных параллельных плоскостей к другой плоскости, имеют одинаковую длину.

Прямые М₁H₁ и M₂H₂ параллельны, так как они перпендикулярны к одной плоскости. Из аксиомы о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, следует, что через две параллельные прямые проходит единственная плоскость (об этом мы упоминали в разделе способы задания плоскости). Тогда будем считать, что через параллельные прямые M₁H₁ и M₂H₂ проходит плоскость . Очевидно, плоскость пересекает плоскости и по прямым М₁М₂ и H₁H₂ . Эти прямые не пересекаются (в противном случае плоскости и имели бы общую точку, что невозможно, так как они параллельны по условию), значит, они параллельны. Таким образом, в четырехугольнике М₁М₂H₂H₁ противоположные стороны попарно параллельны, следовательно, М₁М₂H₂H₁ — параллелограмм (в нашем случае прямоугольник). Следовательно, его противоположные стороны равны. То есть, , что и требовалось доказать.

Следует отметить, что расстояние между параллельными плоскостями является наименьшим из расстояний между произвольными точками этих параллельных плоскостей.

Видео:Расстояние между параллельными плоскостямиСкачать

Нахождение расстояния между параллельными плоскостями – теория, примеры, решения.

Переходим к вопросу нахождения расстояния между параллельными плоскостями.

На уроках геометрии в 10-11 классах расстояние между параллельными плоскостями находится примерно так: строится какой-нибудь перпендикуляр от некоторой точки одной плоскости к другой плоскости и определяется его длина. Для этого, в зависимости от условий задачи, применяется либо теорема Пифагора, либо признаки равенства или подобия соответствующих треугольников, либо определения синуса, косинуса, тангенса угла.

Если же есть возможность ввести прямоугольную систему координат и заданные параллельные плоскости описать с помощью уравнений, то расстояние между параллельными плоскостями можно отыскать методом координат. Давайте детально его разберем.

Сформулируем условие задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и заданы две параллельные плоскости и . Требуется найти расстояние между этими параллельными плоскостями.

Решение будем строить на основе определения расстояния между параллельными плоскостями.

Так как в условии задачи определены плоскости и , то мы можем отыскать координаты некоторой точки М₁ , лежащей на одной из заданных плоскостей (для определенности будем считать, что точка лежит в плоскости ). Также мы можем получить нормальное уравнение плоскости в виде . Тогда искомое расстояние между параллельными плоскостями равно расстоянию от точки до плоскости , которой соответствует нормальное уравнение вида . Это расстояние вычисляется по формуле (ее вывод смотрите в разделе вычисление расстояния от точки до плоскости).

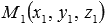
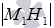
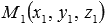
Итак, чтобы найти расстояние между двумя параллельными плоскостями нужно:

• определить координаты точки М₁ , лежащей в одной из заданных плоскостей;
• найти нормальное уравнение другой плоскости в виде ;
• вычислить искомое расстояние по формуле .

В частности, если в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости , а плоскости — общее уравнение плоскости вида , то расстояние между параллельными плоскостями и вычисляется по формуле .

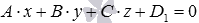
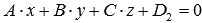
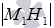
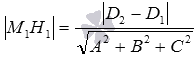
Поясним, как была получена эта формула.

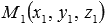
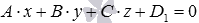
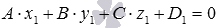
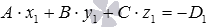
Пусть точка лежит в плоскости . Тогда координаты точки М₁ удовлетворяют уравнению плоскости , то есть, справедливо равенство , откуда имеем . Это равенство мы используем позже.

Нормальное уравнение плоскости в зависимости от знака числа D₂ имеет вид или . Но при любом значении числа D₂ расстояние от точки до плоскости можно вычислить по формуле . Учитывая полученное выше равенство , последняя формула примет вид .

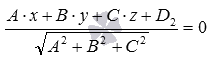
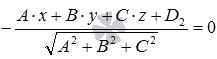
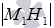
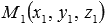
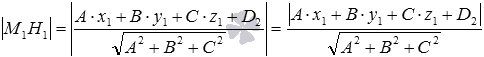
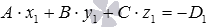
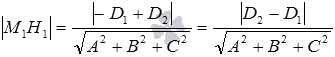
Осталось разобрать решения нескольких примеров.

Найдите расстояние между параллельными плоскостями и , которые в прямоугольной системе координат Oxyz определены уравнениями и соответственно.

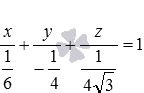
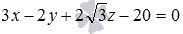
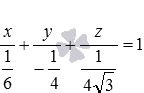
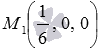
Заданное уравнение плоскости в отрезках вида позволяет легко найти координаты точки М₁ , лежащей в этой плоскости. В качестве точки М₁ возьмем точку, в которой плоскость пересекает ось Ox , то есть, .

Приведем общее уравнение плоскости к нормальному виду:

Теперь вычисляем расстояние от точки до плоскости :
.

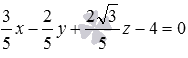
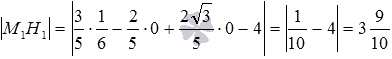
Это и есть искомое расстояние между заданными параллельными плоскостями.

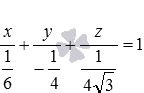
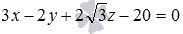
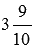
От уравнения плоскости в отрезках перейдем к общему уравнению плоскости: . Чтобы коэффициенты при переменных x , y и z в общих уравнениях плоскостей и стали равными, умножим обе части второго уравнения на два: . Теперь мы можем воспользоваться формулой для вычисления расстояния между параллельными плоскостями: .

.

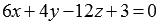
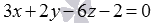
Вычислите расстояние между параллельными плоскостями и .

Очевидно, при таком условии задачи удобно использовать второй способ для нахождения расстояния между параллельными плоскостями. Если умножить обе части второго уравнения плоскости на два, то коэффициенты при переменных x , y и z в уравнениях 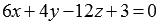и станут равны и можно будет применить формулу: .

Несомненно, можно было использовать первый способ.

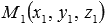
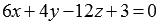
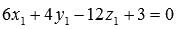
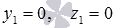
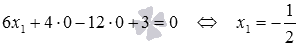
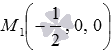
Пусть точка лежит в плоскости , тогда ее координаты удовлетворяют уравнению плоскости, то есть, справедливо равенство . Приняв , вычислим x₁ : . Следовательно, .

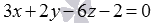
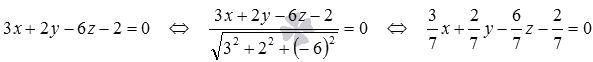
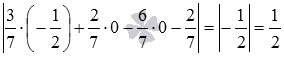
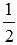
Теперь приведем общее уравнение плоскости к нормальному виду: . Тогда искомое расстояние между параллельными плоскостями равно .

.

🎬 Видео

21. Угол между прямой и плоскостьюСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Видеоурок "Угол между плоскостями"Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Угол между прямыми в пространстве. 10 класс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

14. Угол между прямыми в пространствеСкачать

Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать

Длина отрезкаСкачать