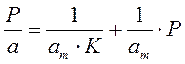Рассчитать постоянные уравнения ленгмюра адсорбции аргона на угле при 78 5

• Реферат.Справочник
• Контрольные работы по химии
• Показать что адсорбция аргона на коксовом угле подчиняется уравнению Фрейндлиха и найти графически константы этого уравнения по следующим данным

Условие

Показать, что адсорбция аргона на коксовом угле подчиняется уравнению Фрейндлиха и найти графически константы этого уравнения по следующим данным: Р, см рт.ст. 11,06 14,93 24,65 36,77 54,8 A, см3/г 11,1 12,78 16,25 19,4 23,8

Решение

При расчетах все данные перевести в систему СИ: давление в Па, адсорбцию – в м3/кг, т. е. 1 см рт. ст. = 1333,3 Па; см3/г = 10–3 м3/кг.
Р· 10-4,Па 1,47 1,99 3,29 4,9 7,31
A· 103, м3/кг 11,1 12,78 16,25 19,4 23,8
Прологарифмируем:
lnP
9,6 9,9 10,4 10,8 11,2
lnA
-4,5 -4,36 -4,12 -3,94 -3,74
Строим линейную зависимость по уравнению Фрейндлиха и находим по данной зависимости постоянные уравнения:
A=k*P1n
lnA=lnk+1nlnP
tgα=1n=lnAA-lnABlnPA-lnPB=-4.5-(-3,94)(9.6-10.8)=0.47
n=1tgα=10.47=2.14
lnk=-9 → k=1.23*10-4
Для установления области применимости уравнения Фрейндлиха к данному виду адсорбции подставляем найденные константы 1/n и 1g k в линейную форму уравнения изотермы:
lnA=-9+0.47lnP
и вычисляем величину 1n А для 5 – 6 значений равновесных давлений (давления берем из графика А = f (P) в широком интервале концентраций)

Видео:Решение задач на термохимические уравнения. 8 класс.Скачать

Адсорбционная теория Ленгмюра

Для описания изотермы по рис. 2.10а используют уравнения вида:

где К и к—константы.

Приведенные уравнение являются основными в теории мономолеку- лярной адсорбции Ленгмюра. Чаще используется первый вариант, так как в случае адсорбции ПАВ справедливы все уравнения, содержащие величину А, поскольку при этом абсолютная и гиббсовская адсорбции практически одинаковы ( А = Г).

При выводе уравнения Ленгмюра физическое взаимодействие на поверхности может быть представлено как квазихимическая реакция:

где А — адсорбционные центры поверхности; В— распределяемое вещество; АВ — комплекс, образующийся на поверхности.

По мерс увеличения концентрации (давления) вещества В равновесие реакции сдвигается в сторону образования комплекса и свободных центров становится меньше. Константа адсорбционного равновесия по закону действия масс имеет вид:

Введем обозначения: [В) = с; [лв]н=Л и [а= Л₀, в которых А — величина адсорбции; А^ — число оставшихся свободными адсорбционных

центров, приходящихся на единицу площади поверхности или единицу массы адсорбента. Если А — величина предельной адсорбции (емкость адсорбционного монослоя), то Подставляя принятые обозначения в уравнение для константы равновесия, получим выражение для константы , которое после преобразований и дает известное уравнение изотермы мономолекулярной адсорбции Ленгмюра:

Для газов вместо концентрации используется давление д (так как концентрация газов и паров при газовой адсорбции практически пропорциональна парциальным давлениям):

Для характеристики адсорбции используется степень заполнения поверхности . Относительно степени заполнения уравнение (2.9)

можно записать в виде

Константы адсорбционного равновесия в разных видах уравнений Ленгмюра (К, к и к’) характеризуют энергию взаимодействия адсорбента и адсорбата: чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия.

Известен другой вариант вывода уравнения Ленгмюра — кинетический, в котором основное внимание уделяется скорости наступления динамичного равновесия процессов адсорбции и десорбции. При этом выводе показывается, что константа адсорбционного равновесия равна отношению констант скорости адсорбции и десорбции:

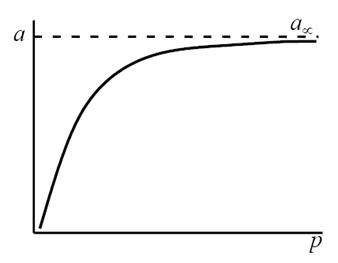
Для анализа изотермы адсорбции по уравнению Ленгмюра воспроизведем типичную изотерму адсорбции по мономолекулярному механизму (рис. 2.26).

Рис. 2.26. Изотерма мономолекулярной адсорбции

Анализ изотермы мономолекулярной адсорбции:

— при очень малых концентрациях, когда с^О, произведением К с в знаменателе можно пренебречь, поэтому получаем А = А_СС-Кс или А = К_Г‘С. Полученные соотношения соответствуют закону Генри и коэффициент пропорциональности К_г — константа Генри. По закону Генри

величина адсорбции с ростом концентрации на участке АВ увеличивается линейно;

— при больших концентрациях или давлениях, когда произведение К-с» 1, адсорбция стремится к предельному значению А = А#. Это соотношение на участке СД отвечает состоянию насыщения поверхности адсорбента молекулами адсорбата, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата;

в области средних концентраций на участке ВС уравнение Ленгмюра применимо в полной форме.

Физический смысл константы Генри, иногда называемый еще константой распределения, поясняют следующие рассуждения. Если поверхностный слой рассматривать как отдельную фазу, то перераспределение вещества между поверхностным слоем и объемом фазы будет происходить до тех пор, пока химические потенциалы обеих фаз не станут равными:

где p_s — химический потенциал в поверхностном слое; p_v— химический потенциал объемной фазы.

Учитывая, что , для равновесного состояния имеем , откуда

Если в области малых концентраций активности считать равными концентрациям, то поверхностная концентрация равна адсорбции

a_s = с_s = А и тогда Из представленных соотношений и полу

чается уравнение Генри: А = Кр-с.

Можно получить подобное выражение через давление, учитывая, что в области малых концентраций газ подчиняется закону состояния идеального газа pV = nRT, откуда . Подставляя послед

нее соотношение в уравнение адсорбции, получаем:

Уравнения Генри просты по виду, но иногда их бывает вполне достаточно для практических расчетов. На твердых поверхностях область действия этого закона мала из-за неоднородности поверхности. Но даже на однородной поверхности обнаруживается отклонение от линейной зависимости при увеличении концентрации (давления). Это объясняется уменьшением доли свободной поверхности, приводящим к замедлению роста адсорбции.

Отклонения от закона Генри учитывает эмпирическое уравнение, установленное Фрейндлихом и Бедекером на основе изучения адсорбции газов на твердых адсорбентах. Позднее это уравнение было теоретически обосновано Зельдовичем и оказалось применимым и для растворов.

Теория мономолекулярной адсорбции была создана Ленгмюром при изучении адсорбции газов на твердых поверхностях. Основные положения теории состоят в следующем:

• — на поверхности твердого адсорбента имеются активные центры, все они энергетически однородны (поверхность эквипотенциальна) и их количество на единице площади постоянно для данного адсорбента;
• — каждый активный ценгр удерживает только одну молекулу адсорбата, которая закреплена с ним силами физической природы (адсорбция обратима). Адсорбированная молекула образует с центром прочный комплекс и не способна перемещаться по поверхности;
• — учитываются только силы взаимодействия молекулы с адсорбционным центром (без учета взаимодействия между молекулами адсорбага).

Несмотря на жесткие ограничения, теория широко используется и даст хорошую сходимость с практическими результатами для большого количества видов адсорбции. В настоящее время она распространяется на адсорбцию на других границах раздела.

Теория Ленгмюра объясняет адсорбцию ПАВ на границе вода — воздух, когда полярная группа, обладая большим сродством к полярной фазе, втягивается в воду, в то время как неполярный радикал выталкивается в неполярную фазу (воздух) и при малых концентрациях углеводородные цепи «плавают» на поверхности воды (это возможно из-за их гибкости). С ростом концентрации цепи поднимаются и в насыщенном адсорбционном слое занимают вертикальное положение, при этом поверхность воды сплошь покрыта «частоколом» из вертикально ориентированных молекул ПАВ. Значение поверхностного натяжения в этом случае приближается к значению чистого жидкого ПАВ на границе с воздухом. Максимальная адсорбция Г_а0 именно поэтому не зависит от длины углеводородного радикала, а определяется только размерами поперечного сечения молекул.

Существование насыщенных адсорбционных слоев позволяет определять размеры молекул ПАВ. Впервые в истории химии размеры молекул были определены именно коллоидно-химическим путем и уже позже подтверждены другими методами. Поскольку в насыщенном слое молекулы плотно упакованы и имеют вертикальную ориентацию, то можно рассчитать важные характеристики мономолекулярного слоя:

— размер поперечного сечения молекул, то есть площадь, занимаемую одной молекулой ПАВ в поверхностном слое («посадочную площадку»):

— длину молекулы ПАВ, равную толщине адсорбционного слоя:

где N_А — число Авогадро, р и М — плотность и молекулярная масса поверхностно-активного вещества.

Для определения постоянных параметров проводят преобразование уравнения Ленгмюра к уравнению прямой линии

Представляя экспериментальные данные в обратных осях или в осях , в первом случае по отрезку, отсекаемому на оси ординат при , определяют величину . Тангенс угла наклона прямой позволяет определить отношение и рассчитать значение пре

дельной адсорбции, по которому можно вычислить адсорбционную константу К. Во втором случае, наоборот, отрезок на ординате связан с величиной обратной предельной адсорбции , а по тангенсу угла наклона

прямой можно определить и затем рассчитать константу К.

Рассмотрим вариант определения констант уравнения Ленгмюра на примере адсорбции в системе вода — изоамиловый спирт. В таблице представлены экспериментальные данные но величинам поверхностного натяжения о растворов различной концентрации с:

Видео:Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

Уравнение изотермы адсорбции Ленгмюра

Конечно, предположение, что молекулы адсорбируются с одинаковой вероятностью на любых участках поверхности, в том числе и уже занятых ранее — слишком грубое допущение, пригодное лишь для очень малых степеней покрытия.

Теория Ленгмюра позволяет учесть наиболее сильные отклонения от закона Генри, что связано с ограничением адсорбционного объема или поверхности адсорбента. Ограниченность этого параметра приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации распределяемого вещества. Это положение уточняется следующими утверждениями.

1) Адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбента — образуется мономолекулярный слой.

2) Адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна.

3) Адсорбированные молекулы не взаимодействуют друг с другом.

Простейший вывод уравнения Ленгмюра, данный Кисилевым, основан на рассмотрении химического (в случае хемосорбции) или квазихимического (в случае физической адсорбиии) равновесия молекула газа + свободное место↔адсорбированная молекула.

Для обычного выражения константы равновесия через концентрации участников рассматриваемого процесса необходимо условиться о способах их выражения. Концентрация адсорбированных молекул может быть выражена не только числом адсорбированных молекул на 1 м 2 поверхности, но и в относительных единицах через долю занятой поверхности (степень заполнения поверхности) θ. Тогда, в тех же единицах, концентрация свободных мест 1-θ. Концентрация молекул газа (а молях на миллилитр) может быть заменена пропорциональной ей величиной давления Р (равновесное давление адсорбата в объеме фазы, граничащей с адсорбентом). Такая свобода в выборе единиц рассматриваемых концентраций обусловлена тем, что соответствующие константы пропорциональности могут быть объединены с константой равновесия. Итак, константа равновесия

. (2.6)

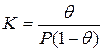
Решение этого уравнения относительно θ приводит к выражению

. (2.7)

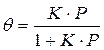
Если а, как и раньше, есть величина адсорбции (моль/см 2 или см 3 /г), а a_m — величина адсорбции, соответствующая полному заполнению поверхности (емкость монослоя, моль/см 2 ), то степень заполнения θ=a/a_m, (2.8)

т.е. 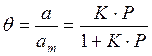, (2.9)

отсюда 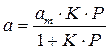(2.10)

В такой форме уравнение Ленгмюра широко известно. Оно содержит две константы: a_m, кратко называемая емкостью монослоя, и K — константа, зависящая от энергии адсорбции и температуры.

Итак, уравнение Ленгмюра – это уравнение монослойной адсорбции на однородной поверхности в отсутствие сил притяжения между молекулами адсорбата.

Посмотрим, какую форму примет уравнение при крайних значениях поверхностной концентрации адсорбированного вещества.

В области малых концентраций, т.е. при малых давлениях, КР >1, и единицей в знаменателе можно пренебречь:

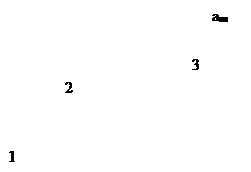
т.е. величина адсорбции стремится к пределу, при котором она уже практически не зависит от давления (участок 3 изотермы адсорбции). В промежуточной области (участок 2) зависимость адсорбции от давления описывается самим уравнением (2.10).

Рис. 2.5. Три участка изотермы адсорбции Ленгмюра

Таким образом, по модели Ленгмюра, вначале адсорбция растет пропорционально давлению газа, затем, по мере заполнения мест на поверхности, этот рост замедляется и, наконец, при достаточно высоких давлениях рост адсорбции практически прекращается, так как покрытие поверхности становится весьма близким к монослойному. Необходимо подчеркнуть, однако, что по этой модели завершение образования монослоя происходит лишь при бесконечно высоком давлении. Форма изотермы адсорбции, предсказываемая уравнением Ленгмюра, экспериментально наблюдается в случае химической адсорбции на однородных поверхностях. Для физической адсорбции такое соответствие наблюдается только в начальной области изотермы. При больших заполнениях не получается предсказываемого теорией приближения к насыщению и изотерма продолжает подъем с ростом давления, причем она становится даже более крутой.

Для удобной проверки приложимости уравнения Ленгмюра к экспериментальным данным преобразуем его в линейную форму. Разделим обе части уравнения (2.10) на Р:

. (2.13)

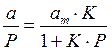
Перевернем дроби по обе части равенства:

. (2.14)

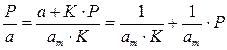
Если по оси абсцисс откладывать Р, а на оси ординат Р/а, то в случае выполнимости уравнения Ленгмюра экспериментальные точки должны укладываться на прямую. Начальной ординатой будет 1/(а_m∙К), тангенсом угла наклона прямой 1/а_m. Из того и другого выражения легко вычислить обе константы a_m и К. Пример такого построения показан на рис. 2.6, где экспериментальные точки для адсорбции бензола на графитированной саже, в соответствии с указанными ранее, легли па прямую только в области малых давлений (до Р/Р₀ =0.1).

Рис. 2.6. Изотерма адсорбции бензола при 20 о С на графитированной саже в координатах линейной формы уравнения Ленгмюра

Имеется немало примеров, когда уравнение Ленгмюра не выполняется. Объясняется это тем, что не оправдываются оба допущения теории об однородности поверхности и отсутствии взаимодействия молекул, особенно первое из них. Тот факт, что имеются случаи адсорбции на реальных неоднородных поверхностях, когда уравнение Ленгмюра все же удовлетворительно описывает экспериментальные данные, Брунауер объясняет тем, что в некотором интервале адсорбция происходит не на всей поверхности адсорбента, а только на части ее, именно на местах с примерно одинаковой теплотой адсорбции. Тогда в этом интервале уравнение Ленгмюра будет справедливо. После того, как эти места заполнены, начинает заполняться следующая серия мест с меньшей теплотой адсорбции. Поэтому для совокупности всех мест поверхности уравнение Ленгмюра может быть непригодно, а для части этих мест — справедливо. Отсюда, выполнимость его для разных адсорбентов зависит от соотношения участков с разной теплотой адсорбции.

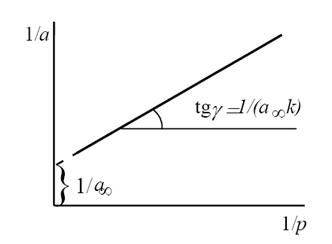
Константы уравнения (2.10) K и a_m могут быть определены графическим способом (рис. 2.7). Для этого уравнение Ленгмюра приводят к следующему линейному виду, разделив единицу на уравнение (2.10):

(2.15)

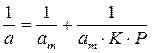
Рис. 2.7. Линейная форма уравнения изотермы Ленгмюра (a_∞=a_m)

Зная емкость монослоя, можно определить удельную поверхность адсорбента S_уд (м 2 /г или см 2 /г) если известна площадь ω, занимаемая частицей в плотном адсорбционном слое (площадь, занимаемая одной молекулой азота в адсорбционном слое ω = 0.162 нм 2 ):

, (16)

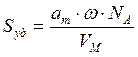
где а_m — емкость монослоя — это количество адсорбата, которое может разместиться в полностью заполненном адсорбционном слое толщиной в 1 молекулу — монослое – на поверхности единицы массы (1г) твердого тела; ω — средняя площадь, занимаемая молекулой адсорбата в заполненном монослое, N_A — число Авогадро (6,022·10 23 молекул/моль); V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Уравнение Ленгмюра можно использовать только при адсорбции в мономолекулярном слое. Это условие выполняется при хемосорбции, физической адсорбции газов при меньшем давлении и температуре выше критической.

Однако в большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и поэтому остается возможность влияния поверхностных сил на второй и т.д. адсорбционные слои. Это реализуется в том случае, когда газы и пары адсорбируются при температуре ниже критической, т.е. образуются полимолекулярные слои на поверхности адсорбента, что можно представить как вынужденную конденсацию В этом случае используют уравнение БЭТ (Брунауер –Эммет — Теллер).

Пример 2.1. При адсорбции азота на активированном угле при 220К получены следующие данные:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 7 14 23 32 51

Плотность газообразного азота ρ=1,2506 кг/м 3 . Площадь, занимаемая одной молекулой азота в насыщенном монослое, составляет ω = 0.162 нм 2 . V_M — молярный объем адсорбата (газа) (V_M = 22,41 л/моль=22,41∙10 -3 м 3 /моль).

Постройте изотерму адсорбции в линейных координатах. Графически определите константы а_m и К уравнения Ленгмюра, пользуясь которыми, постройте изотерму Ленгмюра. Определите удельную поверхность активированного угля S_уд.

Решение. Линейная форма уравнения Ленгмюра выражается (2.15):

.

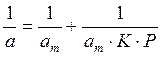
Определим 1/а_m и 1/ р:

(1/р)·10 -3 , Па 0,1883 0,1020 0,0556 0,0303 0,0143

1/а·, см 3 /г 0,143 0,071 0,043 0,031 0,020

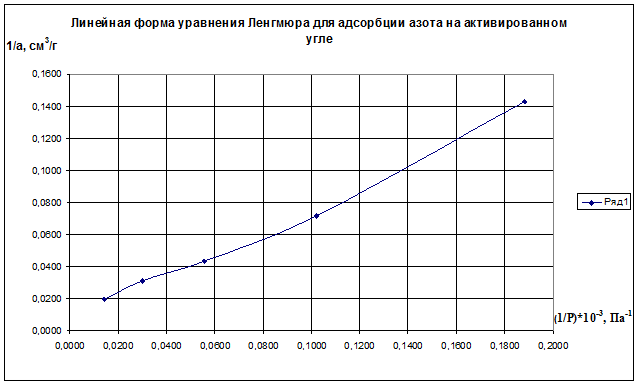
Строим график зависимости 1/а=f(1/р)∙10 -3 (рис.2.8). По графику находим 1/а_m как отрезок, отсекаемый прямой на оси ординат, для чего необходимо продлить полученную прямую до пересечения с осью ординат.

Рис.2.8. Линейная форма уравнения Ленгмюра для адсорбции азота на активированном угле

Уравнение прямой y=a+bx, имеет следующее формульное выражение:

Это выражение может быть определено с помощью регрессионного анализа в Microsoft Excel (встроенного пакета Анализ данных — Регрессия по значениям 1/а_m и 1/ р).

Из уравнения получим 1/a_m=0,00698 г/см 3 .

Откуда получим: a_m=143,35 см 3 /г.

Далее находят тангенс угла наклона прямой к оси абсцисс tgα=1/(a_m∙K) по графику (или по уравнению регрессии). tgα=0,70099. Тогда, зная значения a_m и tgα, можно определить K=9,95 кг/м 3 .

Теперь, зная константы а_m и К уравнения Ленгмюра, построим изотерму Ленгмюра, для чего рассчитаем по формуле (2.10) значения а для различных значений Р и получим:

Р, Па 5310 9800 18000 33000 70000

a, cм 3 /г 140,69 141,90 142,56 142,92 143,15

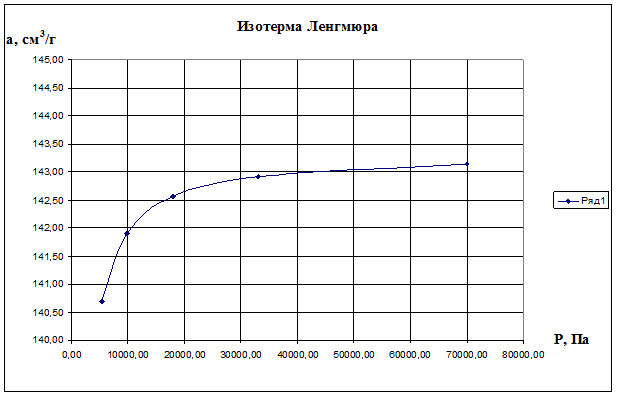
По данным значениям построим изотерму Ленгмюра а=f(P), представлена на рис.2.9.

Рис. 2.9. Изотерма Ленгмюра а=f(P)

По формуле (2.16) рассчитаем удельную поверхность активированного угля: 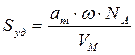и получим S_уд=624,05 м 2 /г.

В случае, когда известна плотность вещества (адсорбента) ρ и молярная масса M, а не известен V_M — молярный объем адсорбата удельную поверхность вещества (активированного угля) находят по формуле:

где a_m выражают в моль/кг.

Для азота М= 0,0280 кг/моль, ρ=1,2506 кг/м 3 .

Из расчетов видно, что два способа расчета S_уд дают почти одинаковые результаты.

Пример 2.2. Удельная поверхность непористой сажи равна 73,7м 2 /кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

Р, Па 1,03 1,29 1,74 2,50 6,67

а∙10 2 , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Решение. Используем линейную форму записи уравнения Ленгмюра, заданную формулой (2.14):

Рассчитываем значения Р/а:

(Р/а)∙10 -2 , Па∙кг/моль 0,656 0,668 0,68 0,712 0,879

Р, Па 1,03 1,29 1,74 2,50 6,67

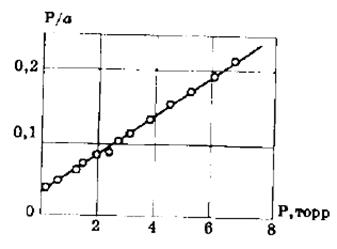
По этим данным строим график в координатах уравнения Ленгмюра в линейной форме P/a=f(P).

Из графика находим а_m= Р/(Р/а) = 25,2∙10 -2 моль/кг.

Удельная поверхность адсорбента связана с емкостью слоя а_m, выраженного в моль/кг, соотношением: S_уд=a_m∙ω∙N_A (2.18)

Площадь, занимаемая молекулой бензола в плотном монослое, равна

ω = S_уд/(a_m N_A) ==73,7 10 3 /(6,02 10 23 ∙25,210 -2 )=0,49∙10 -18 м 2 =0,49 нм 2 .

📹 Видео

Уравнение ЛенгмюраСкачать

Поверхностные явления. Адсорбция.Скачать

Расчеты по уравнениям химических реакций. 1 часть. 8 класс.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Меняем порядок слагаемых: меняется сумма. Теорема Римана. Высшая математикаСкачать

Как расставить коэффициенты в органических ОВР? | Екатерина СтрогановаСкачать

❗️МОЙ СЕКРЕТНЫЙ МЕТОД ВОССТАНОВЛЕНИЯ ОРХИДЕЙ МЕТОД 12/12 И ОРХИДЕЯ БЕЗ КОРНЕЙ С ЛИСТЬЯМИ-ТРЯПОЧКАМИ!Скачать

ВАЛЕНТНОСТЬ | Как определить валентность | Как составить химическую формулу по валентностиСкачать

№18. Система уравнений с параметром (профильный ЕГЭ)Скачать

Расчет рН растворов сильных и слабых оснований. Химия для поступающих.Скачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Расчеты по уравнениям химических реакций. 2 часть. 8 класс.Скачать

РЕАКЦИИ ИОННОГО ОБМЕНА и условия их протекания | Как составлять молекулярные и ионные уравненияСкачать

Гипотеза Римана - Numberphile на русском.Скачать

8 класс, 25 урок, Формула корней квадратного уравненияСкачать

Параметры с нуля. Линейные уравнения и неравенстваСкачать

✓ Самое простое логарифмическое уравнение | Резерв досрока ЕГЭ-2019. Задание 12 | Борис ТрушинСкачать