Уравнение Бернулли широко применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов, насосов и т.п. На его основании сконструирован ряд приборов и устройств, таких как расходомер Вентури, карбюратор, водоструйный насос (эжектор), трубка Пито и т.д.
Измерение скорости потока и расхода жидкости
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.2.10), загнутый конец которой направлен навстречу потоку.
Трубка полного напора, или трубка Пито , служит для измерения скорости потока, например в трубе. Если установить в одном сечении потока трубку, изогнутую под углом 90, отверстием навстречу потоку и пьезометр, то жидкость в трубке поднимется над уровнем жидкости в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, следовательно, давление увеличивается на величину скоростного напора. Измерив, разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.
Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
где Н — столб жидкости в трубке Пито.
Рис. 2.10 Трубка Пито и pасходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.2.10). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование. Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в сужающемся месте возрастает, а давление падает. Возникает разность (перепад) давлений, которую можно измерить двумя пьезометрами или дифференциальным U-образным ртутным манометром.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:
Используя уравнение неразрывности
сделаем замену в получено выражении:
Решая относительно Q, получим
Выражение, стоящее перед 

Карбюратор поршневых двигателей внутреннего сгорания (рис.2.11) служит для подсоса бензина и смешивания его с потоком воздуха. Поток воздуха, засасываемого в двигатель, сужается в том месте (сечение 2-2), где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.
Рис. 2.11. Схема карбюратора
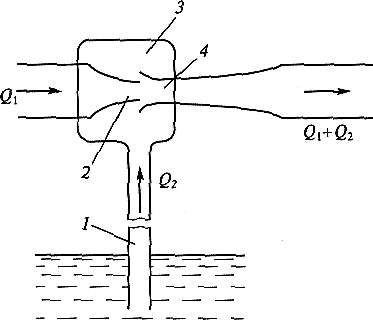
Рис. 2.12. Схема струйного насоса (эжектора):
1 — труба; 2 — насадок; 3 — камера; 4 — расширяющаяся трубка
Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

— Примеры применения уравнения Бернулли
7.5. Примеры применения уравнения Бернулли.
Рассмотрим примеры применения уравнения Бернулли.
1. Расходомер Вентури
Для определения скорости и расхода жидкости часто используется расходомер Вентури. Измерим статическое давление p1 и p2 в поперечных сечениях с различными площадями.

Интеграл Бернулли для сечений 1 и 2 принимает вид


Видео:Закон БернуллиСкачать

Рекомендуемые материалы
Из уравнения равенства расходов для двух сечений 1 и 2 имеем


Для вычисления показания дифференциального манометра запишем условие равновесия

Собирая все результаты, получаем

Формула используется для определения скорости в трубе. Hа практике для повышения точности иногда вводят эмпирический коэффициент, учитывающий гидравлические потери в трубке Вентури.
2. Измерение скорости
Для измерения кинетической энергии используется трубка полного давления, которая устанавливается в точке измерения открытым концом против потока жидкости ( рис. 30 ).
Струйка жидкости, подтекающая к открытому концу трубки, полностью замораживается (v=0) и весь скоростной напор превращается в давление, которое в сумме со статическим достигает давления торможения 


Таким образом измерение скорости жидкости или «несжимаемого» газа (M 0, то начинается процесс образования пузырьков пара (кипение), и неразрывность течения капельной жидкости нарушится.
Далее смесь капельной жидкости и пузырьков пара попадает в расширяющийся канал, давление возрастает и пузырьки пара начинают конденсироваться.
Кавитацией называется совокупность процессов образования пузырьков пара и их конденсация.
Кавитация может возникать не только в трубопроводах, но и при внешнем обтекании тел в областях, где возрастают местные скорости и уменьшается давление. Кавитации подвержены быстроходные колеса насосов и турбин, гребные винты.
Конденсация пузырьков пара происходит на твердых поверхностях очень быстро и завершается гидравлическим ударом, при котором развивается местное ударное давление на твердых поверхностях, достигающее сотен и даже тысяч атмосфер. Поэтому кавитация сопровождается тряской, шумом, снижением КПД насосов и турбин, эрозией твердых поверхностей, а иногда и выходом из строя агрегатов.
Обычно работа гидравлических систем в условиях кавитации не достигаются. Для предотвращения кавитации минимальное давление жидкости в системе должно быть больше давления паров, насыщающих пространство.
Одним из способов предотвращения кавитации является снижение температуры жидкости. Это приводит к снижению давления паров, насыщающих пространство.
Например, вода при 373К кипит при давлении

Для оценки возможности возникновения кавитации используется безразмерный критерий — число кавитации

Значение, числа кавитации при котором она возникает, называется критическим 
Явление используется в кавитационных регуляторах расхода.
4. Формула Торричелли
Применим интеграл Бернулли для определения скорости истечения тяжелой несжимаемой жидкости из большого открытого сосуда через малое отверстие( рис. 32).

Здесь S1— площадь свободной поверхности, S2 – площадь отверстия, v1 и v2 — скорости на поверхности и в отверстии.
Уравнение неразрывности принимает вид

Считая движение жидкости установившимся и безвихревым, применим интеграл Бернулли



Из уравнения неразрывности


Если отношение 


Пример. Определить форму сосуда вращения, употребляемого для водяных часов( рис. 33).
Приведем формулы решения задачи






где 
Используя уравнение Бернулли можно объяснить принцип действия :
1) работы струйного насоса, в котором высоконапорный поток G1 используется для подачи жидкости G2 из резервуара ( рис. 34).
2) принцип наддува топливного самолетного бака для предотвращения кавитации в топливной системе при полетах на большой высоте ( рис. 35 )
3) причину повышения подъемной силы крыла при заданной картине линий тока ( рис. 36 )
Уменьшение давления в точках, где скорость потока больше, положено в основу водоструйного насоса. Струя воды подается в трубку, открывающуюся в атмосферу, так что на выходе их трубки давление равно атмосферному. В трубке имеется сужение, по которому вода идет с большой скоростью, вследствие чего давление в этом месте оказывается меньше атмосферного. Такое же давление устанавливается и в охватывающей трубку камере насоса, которая сообщается с трубкой через разрыв, имеющийся в узкой части трубки. Подсоединив к камере насоса откачиваемый объект, из него можно откачать воздух (или какой-либо другой газ) до давления порядка 100 мм рт. ст. Откачиваемый воздух захватывается струей воды и уносится в атмосферу.
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Лабораторная работа Гидравлика. МУлабМЖГ_рус_2011. Методические указания по выполнению лабораторных работ по дисциплинам Гидравлика, Механика жидкостей и газов
| Название | Методические указания по выполнению лабораторных работ по дисциплинам Гидравлика, Механика жидкостей и газов |
| Анкор | Лабораторная работа Гидравлика |
| Дата | 08.04.2021 |
| Размер | 1.37 Mb. |
| Формат файла |  |
| Имя файла | МУлабМЖГ_рус_2011.doc |
| Тип | Методические указания #192517 |
| страница | 5 из 6 |
 С этим файлом связано 1 файл(ов). Среди них: РГР.docx. С этим файлом связано 1 файл(ов). Среди них: РГР.docx.  Показать все связанные файлы Подборка по базе: методические указания по выполнению КР ( 1 раздел) (1).pdf, Методические указания по оформлению текста ВКР и курсовых работ., Рекомендации к выполнению ПрофЭт.docx, 2. Методические рекомендации инструктору по ФОС для по Спас шлюп, Сборник лабораторных работ по дисциплине ОП.10 _Информационная б, Методические указания по выполнению лабораторной работы №4.docx, Методические указания по Математической статистике.pdf, Перечень лабораторных работ.pdf, Указания к выполнению практической работы 11.docx, Метод указания к семинарским занятиям по Педагогике.docx Показать все связанные файлы Подборка по базе: методические указания по выполнению КР ( 1 раздел) (1).pdf, Методические указания по оформлению текста ВКР и курсовых работ., Рекомендации к выполнению ПрофЭт.docx, 2. Методические рекомендации инструктору по ФОС для по Спас шлюп, Сборник лабораторных работ по дисциплине ОП.10 _Информационная б, Методические указания по выполнению лабораторной работы №4.docx, Методические указания по Математической статистике.pdf, Перечень лабораторных работ.pdf, Указания к выполнению практической работы 11.docx, Метод указания к семинарским занятиям по Педагогике.docx8 Содержание отчета: — схема испытательного стенда; — порядок проведения опытов и обработки экспериментальных данных (включая журнал измерений и вычислений); — краткие выводы. 1. Чем обусловлены потери энергии при движении жидкости в прямых трубах постоянного диаметра? 2. Какие показатели влияют на коэффициент гидравлического сопротивления по длине трубопровода? 3. Как определить коэффициент гидравлического сопротивления при ламинарном режиме движения? 4. Как определяется коэффициент гидравлического сопротивления при турбулентном режиме движения? 5. Что характеризует коэффициент Шези? 6. Какие факторы влияют на коэффициент гидравлического сопротивления по длине при турбулентном режиме движения? 7. Объясните порядок проведения опыта и поставленной задачи? Лабораторная работа № 6 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА РАСХОДА РАСХОДОМЕРА ВЕНТУРИ Определить расход жидкости в трубопроводе, используя расходомер Вентури. — изучить примеры использования уравнения Бернулли при решении гидравлических задач и в технике; — установить взаимосвязь между скоростью жидкости и рабочим давлением при ее движении в трубопроводе переменного сечения; — ознакомиться с методикой теоретического и экспериментального определения расхода жидкости в трубопроводе. — изучить содержание методического указания и теоретический материал, связанных с данной работой; — ответить на контрольные вопросы; — ознакомиться с испытательным стендом и порядком проведения лабораторной работы; — обработать результаты исследований и представить в виде таблиц; — оформить и защитить отчет по лабораторной работе. Лабораторный испытательный стенд и методические указания. Уравнение Бернулли является основным законом установившегося движения жидкости, позволяющего рассмотреть и понять работу ряда гидравлических устройств. При помощи уравнения Бернулли, например, определяется высота всасывания насоса и производится расчет всасывающих линий, а также расчет маслопроводов и других транспортных линий. В гидравлике практически нет разделов, где в той или иной степени не использовалось бы уравнение Бернулли. Конкретным примером применения уравнения Бернулли в технике является расходомер Вентури. Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах, при помощи которого производится измерение расхода жидкости. Расходомер Вентури, схема которого изображена на рисунке 6.1, состоит из конусообразной, сходящейся трубы со вставкой меньшего диаметра, чем диаметр основной цилиндрической трубы. По оси расходомера устанавливаются два пьезометра: один перед началом конусообразного сужения, а другой посередине суженной вставки. Применим уравнение Бернулли к потоку жидкости, движущемуся по расходомеру Вентури. Проведем плоскость сравнения 0-0 по оси и рассмотрим два сечения I и II. Вследствие незначительной длины между указанными сечениями (обычно 3-5 диаметров трубы) и плавного конусообразного подхода к суженной вставке потерями энергии на преодоление сопротивлений можно пренебречь. Поэтому уравнение Бернулли применительно к рассматриваемому случаю запишется следующим образом: Согласно схеме, изображенной на рисунке 6.1 имеем: — плоскость сравнения 0-0 проходит через центры тяжестей сечений I и II; —D – диаметр основания трубопровода; d– диаметр суженной вставки; -v1 иv2 – соответственно скорости движения жидкости в сечения I и II диаметром трубопроводов D и d; — S1 и S2 – соответственно площади живых сечений на участках I и II. На основании сплошности и неразрывности потока жидкости расход в I сечении равен расходу в II сечении v1S1= v2S2 или v1 Следовательно, скорость во втором сечении будет равна v2 = v1 Подставим значение v2 в уравнение (6.1) где α1 и α2 – коэффициенты неравномерности распределения скоростей по сечению потоков; ∆h – разность показаний пьезометров, установленных в I и II сечениях Из уравнения (6.4) определим скорость v1 движения жидкости в I сечении Расход жидкости равен В уравнении (6.6) не учитываются потери при движении жидкости через расходомер, вызванные местными гидравлическими сопротивлениями и вязкостным трением. Эти потери учитываются коэффициентом расхода μ 6 Описание лабораторного испытательного стенда Испытательный стенд (рисунок 6.5) состоит из питающего трубопровода 1 и двух вентилей В6 и В7. Вентиль В6 служит для заполнения системы трубопровода рабочей жидкостью, а вентиль В7 для пропуска определенного расхода через расходомер Вентури. Вентиль В12 предназначен для выпуска жидкости из мерного бачка МБ. Мерный бачок необходим для экспериментального определения расхода жидкости, протекающей через расходомер. Пьезометры П14 и П13 установлены, соответственно в большем и меньшем сечениях трубопровода и показывают величину давления, согласно установленной скорости течения жидкости. После ознакомления с испытательным стендом опыты проводятся в следующем порядке:
Рисунок 6.5 – Схема лабораторного стенда На основе данных наблюдений и замеров определяют а) расход жидкости, полученный экспериментальным путем где W – объем мерного бачка (W=0.24×0.2×0.2 м 3 ); б) расход жидкости, полученный расчетным путем, где в) сравнить расходы, полученные экспериментальным и теоретическим (расчетным) путями. Определить в % погрешность расходомера Вентури. Опыт повторяют 2…3 раза. Данные измерений и вычислений занести в таблицу 6.1.
| ||||||||||||||||||||||||||||||||||||||||||||||||














 . (6.1)
. (6.1) = v2
= v2  . (6.2)
. (6.2) . (6.3)
. (6.3)

 , (6.4)
, (6.4) (6.5)
(6.5) . (6.6)
. (6.6)


 , (7.2)
, (7.2) .
. .
. , (7.3)
, (7.3) . (7.4)
. (7.4)
 , (7.6)
, (7.6) .
.















