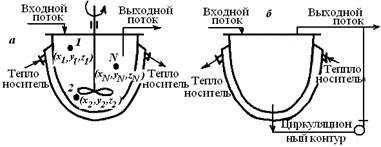
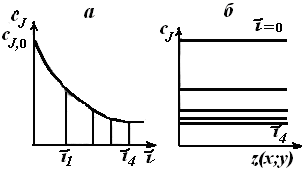
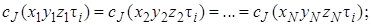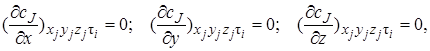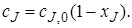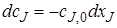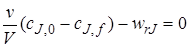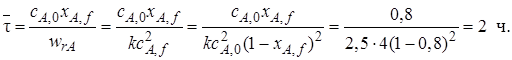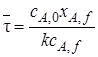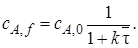Для модели идеального смешения принимается ряд допущений. Допускается, что в результате интенсивного перемешивания устанавливаются абсолютно одинаковые условия в любой точке реактора: концентрации реагентов и продуктов, степени превращения реагентов, температура, скорость химической реакции и т. д. Например, в некоторый момент времени τj во всех точках ректора (рис. 5.1) выполняются следующие условия:
где x, у, z – пространственные координаты.
В проточном реакторе идеального смешения концентрации элементов реакции в выходном потоке в рассматриваемый момент времени τi строго равны концентрациям тех же веществ в реакторе.
Чтобы перечисленные допущения могли быть выполнены, необходимо принять еще одно допущение: переход от одной концентрации к другой в реакторе идеального смешения не должен иметь протяженности во времени. Изменение концентрации исходного реагента от начальной cJ,0 во входном потоке в данный момент времени τi до концентрации в реакторе сJ в этот же момент времени должно происходить мгновенно (скачкообразно).
Приблизиться к режиму идеального смешения можно, обеспечив интенсивное перемешивание реакционной смеси механическими мешалками разного типа или циркуляционными насосами, создающими высокую кратность циркуляции. Смешение, близкое к идеальному смешению, легче выполнить в емкостных аппаратах с приблизительно равным диаметром и высотой.
Так как в реакторе идеального смешения концентрации элементов реакции равномерно распределены по объему, то уравнение материального баланса (4.7), выведенное для элементарного объема, можно распространить на полный объем реактора.
Рассмотрим два частных случая: периодический реактор идеального смешения и проточный реактор идеального смешения, работающий в стационарном режиме.
Периодический реактор идеального смешения.В периодический реактор все реагенты вводят до начала реакции, а все продукты выводят из него только по окончании процесса. В ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, изменяется лишь ее состав. При составлении математического описания принимают, что реакционная смесь однородна по объему аппарата и ее состав зависит только от времени пребывания в периодическом реакторе.
Рис. 5.1. Схемы реакторов идеального смешения
с механическим перемешивающим устройством (а)
и циркуляционным контуром (б)
Из общего уравнения материального баланса (4.7) в случае периодического реактора идеального смешения можно исключить два первых оператора, описывающих явления конвективного и диффузионного переноса вещества в аппарате. При отсутствии перемещения потока через реактор в произвольный момент времени между началом и окончанием процесса средняя линейная скорость элемента потока равна нулю, следовательно, и конвективный перенос в непроточном реакторе отсутствует. Заключение об отсутствии диффузионного переноса вытекает из допущений модели идеального смешения, так как диффузия возможна лишь при наличии градиента концентраций, а при равномерном распределении концентраций по объему он равен нулю. (Этот вывод справедлив не только для периодического, но и для проточного реактора идеального смешения.)
Следовательно, уравнение материального баланса для периодического реактора идеального смешения примет вид
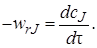
В уравнении (5.1) частная производная заменена на полную, так как в соответствии с допущениями идеального смешения концентрация с внутри реактора является функцией только одной переменной – времени.
Уравнение материального баланса периодического реактора идеального смешения (5.1) совпадает с уравнением (3.2), дающим определение скорости химического превращения. Из одинакового вида уравнений косвенно можно сделать вывод, что гидродинамическая обстановка в периодическом реакторе идеального смешения не накладывает ограничений на химическую кинетику.
Для проведения расчетов по уравнению (5.1) в его левую часть вместо wrJ(cJ)вводят конкретное кинетическое уравнение. Тогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации сJ,f):
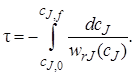
Если вещество J – исходный реагент, то концентрацию cs можно выразить через его степень превращения:
и уравнение (5.2) примет вид
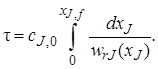
Уравнения (5.2) и (5.3) позволяют также рассчитать зависимость концентрации реагента сJ или его степени превращения хJ от времени пребывания в реакторе (продолжительности реакционного цикла). В разные моменты времени условия в периодическом реакторе различные (концентрация реагентов, продуктов, скорость реакции и т. д.), однако в каждый данный момент времени из-за допущения об идеальности эти параметры строго одинаковы в объеме реактора (рис. 5.2).
Время, рассчитанное по уравнению (5.2) или (5.3), является «чистым» временем, необходимым для проведения химического превращения. Однако для осуществления процесса в периодическом реакторе кроме этого «реакционного» времени нужно затратить вспомогательное время на загрузку реагентов, выведение реактора на нужный технологический режим, разгрузку и очистку. Полное время одного цикла работы периодического реактора суммируется из основного τхр и вспомогательного τвсп.
Рис. 5.2. Изменение концентрации исходного реагента
в периодическом реакторе идеального смешения во времени (а)
и по объему аппарата (б)
Наличие τвсп как составной части времени цикла приводит к снижению производительности химического реактора (количество продукта, получаемого в единицу времени) и является одним из существенных недостатков периодических процессов вообще. Другие их недостатки – большие затраты ручного труда, сложность решения задач автоматизации (так как условия в реакторе во времени постоянно меняются).
Однако периодические реакторы обычно можно приспособить к широкому диапазону условий реакций, что удобно при необходимости производить на одной установке различные химические продукты, например, в промышленности химических реактивов.
Периодические реакторы с интенсивным перемешиванием, приближающимся к идеальному смешению, применяют в производствах реактивов, органических красителей, лекарственных препаратов – там, где для достижения достаточной глубины превращения требуется сравнительно длительное время, а объемы производства невелики.
Периодические реакторы смешения часто применяют в микробиологической промышленности для культивирования аэробных микроорганизмов. Процесс культивирования для большинства микроорганизмов длится 48–72 ч, т. е. достаточно длителен. Интенсивное перемешивание в ферментаторе позволяет обеспечить равномерное распределение температуры, что особенно важно в таких процессах, так как даже небольшие локальные разогревы могут привести к гибели микроорганизмов. Изолированность реакционной системы в периодическом реакторе позволяет устранить опасность отравления микроорганизмов случайными примесями, которые могут попасть в аппарат при непрерывной подаче реагентов.
Окончательное решение о целесообразности применения периодического или непрерывного процесса можно вынести лишь на основании экономической оценки (сравнения расходов на эксплуатацию, амортизацию, электроэнергию, пар, сырье и т. д.). Как правило, при проведении такого сравнения оказывается, что периодические процессы выгодны при относительно невысокой производственной мощности в тех случаях, когда получают дорогостоящие продукты.
Проточный реактор идеального смешения в стационарном режиме.Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме.
Рассмотрим уравнение материального баланса для стационарного проточного реактора идеального смешения без циркуляции. Получим его, опять упрощая общее уравнение материального баланса (4.7). Для любого реактора идеального смешения, и в частности для проточного, из уравнения можно исключить оператор, описывающий диффузионный перенос. При стационарном режиме работы реактора из уравнения исключается производная дсJ/дτ,не равная нулю только при наличии накопления вещества в реакторе.
Таким образом, в уравнении остаются только два члена, описывающие конвективный перенос вещества J и расход или образование этого вещества в ходе химической реакции.
Оператор конвективного переноса (переноса импульса), записанный в уравнении (4.7) в дифференциальной форме, можно представить для проточного реактора идеального смешения в конечно-разностной форме. В соответствии с допущениями модели идеального смешения в проточном реакторе происходит дискретное конечное (а не бесконечно малое) изменение концентрации ∆сJ сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации ∆сJ к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью 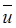
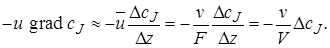
В выражении (5.4) ∆сJ равно разности концентраций на выходе из реактора cif и на входе в реактор сJ,0. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
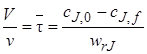
Это же уравнение можно получить и другим путем. Как указывалось, в качестве элементарного объема для реактора идеального смешения можно принять полный объем реактора V. При стационарном режиме работы реактора не происходит изменения постоянных по объему концентраций элементов реакции и во времени, следовательно, в качестве элементарного промежутка времени можно принять любой конечный временной интервал, например единицу времени (1 с, 1 мин или 1 ч).
Количество вещества J, которое за единицу времени войдет в реактор с конвективным потоком, будет равно v0cJ,0,где v0 – объемный расход реакционного потока на входе в аппарат. За это же время выйдет из реактора с конвективным потоком количество вещества J = vfcJ,f,а расход вещества J (или его образование) в ходе химической реакции составит wrJ V. При этом скорость wrJ определяется концентрацией cJ,f.
Стационарность процесса в проточном реакторе можно обеспечить, если объемные расходы на входе v0 и выходе vf равны между собой
(v0 = vf = v).
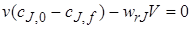
Очевидно, что уравнение (5.6) тождественно уравнению (5.5).
Величина 
Действительное время пребывания частиц в проточном реакторе смешения является случайной величиной в отличие от времени пребывания реагентов в периодическом реакторе. Пусть, например, в реактор введено N одинаковых частиц. В периодическом реакторе все они будут находиться равное время от загрузки до выгрузки. В проточном реакторе идеального смешения эти частицы мгновенно и равномерно распределяются по всему объему аппарата, и так как из аппарата непрерывно выходит поток продуктов, то в момент ввода частиц в реактор какое-то их количество может сразу же оказаться в выходном потоке. Некоторые частицы, равномерно распределяясь в новых порциях реакционной смеси, вошедшей в аппарат, могут находиться в нем бесконечно долго. Отсюда можно сделать вывод, что действительное время пребывания частиц в проточном реакторе – это случайная величина, которая может изменяться от 0 до ∞. Непрерывную случайную величину можно задать с помощью вероятностных характеристик, в частности функций распределения случайной величины. Использование в качестве характеристики времени пребывания частиц в проточном реакторе величины 
Для решения практических задач удобно концентрацию реагента cJ,fвыразить через его степень превращения хJ,f:
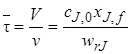
Уравнения материального баланса (5.5)–(5.7) для проточного реактора идеального смешения в стационарном режиме имеют ряд отличий от соответствующих уравнений для периодического реактора (5.2) и (5.3). Следует отметить, что балансовые уравнения стационарного реактора идеального смешения записываются сразу в виде конечного алгебраического уравнения в отличие от дифференциальной формы исходных уравнений для периодического реактора.
В уравнение для периодического реактора скорость wr,Jследует подставлять в виде функциональной зависимости от концентрации wr,J(cj) или степени превращения wr,J(xj) и лишь после интегрирования уравнения возможна подстановка числовых значений. Этот факт, как и дифференциальная форма уравнений материального баланса, отражает зависимость параметров процесса в периодическом реакторе от времени. В стационарном режиме в любой точке реактора идеального смешения в любой момент времени концентрация постоянна. Следовательно, скорость реакции характеризуется каким-то одним конкретным числовым значением, определяемым этой концентрацией. Это число может быть сразу поставлено в уравнение материального баланса.
Пример 5.1.Рассчитать среднее время пребывания реагентов в проточном реакторе идеального смешения, необходимое для достижения степени превращения исходного реагента хА,f= 0,8.
В реакторе протекает реакция второго порядка 2А 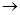
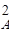
Решение. Для определения 
Таким образом, для достижения степени превращения хА = 0,8 необходимо, чтобы соотношение между объемом реактора и объемным расходом через него 
Уравнения материального баланса для проточного реактора могут быть использованы не только для определения среднего времени пребывания 

Решение этой задачи не вызывает никаких затруднений, если скорость реакции описывается сравнительно простыми кинетическими уравнениями (уравнениями первого и второго порядка). Например, для реакции первого порядка А 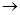
Зачастую скорость сложных реакций с невыясненным до конца механизмом выражают в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным и приходится прибегать к численным методам расчета. В качестве примера рассмотрим весьма наглядный графический метод определения концентрации реагентов на выходе из стационарного проточного реактора идеального смешения.
Запишем уравнение материального баланса (5.5) в следующем виде:
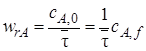
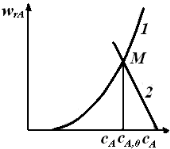
Уравнение (5.8) представляет собой равенство двух разных функций от концентрации. В левой части уравнения записана функция wrА(сА), представляющая собой кинетическое уравнение реакции. В соответствии с законом действующих масс скорость химических реакций пропорциональна концентрациям реагентов, следовательно, wrA(cA) – это возрастающая функция, которую легко представить графически (рис. 5.3, линия 1). Она пересекает ось абсцисс в точке, соответствующей равновесной концентрации сА,е для обратимых реакций, или исходит из начала координат в случае необратимых реакций.
Рис. 5.3. Зависимость скорости реакции от концентрации реагента
на выходе из проточного реактора идеального смешения,
используемая для определения конечной концентрации
В правой части уравнения (5.8) записана соответствующая уравнению материального баланса стационарного реактора идеального смешения линейная функциональная зависимость скорости реакции от концентрации исходного реагента, имеющая отрицательный угловой коэффициент (–1/ 
Уравнению (5.8) удовлетворяют такие значения концентраций сА, при которых значения функций, стоящих в левой и правой частях этого уравнения, равны. Иначе – такие концентрации, при которых графики этих функций пересекаются. Как видно, линии 1 и 2 пересекаются в единственной точке М.Абсцисса этой точки и есть искомая концентрация реагента на выходе из реактора идеального смешения.
Дата добавления: 2015-06-17 ; просмотров: 7956 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Модели реакторов идеального вытеснения и идеального смешенияСкачать

Реактор идеального смешения
Непрерывного действия
Схема потоков в реакторе полного смешения представлена на рис. 1. В реакторе такого типа концентрация любого компонента равномерна по всему реакционному объему, и поэтому уравнение материального баланса можно записать для всего объема реактора. Для установившегося режима:
где Gпр – масса вещества, поступающего в элементарный объем в единицу времени; Gух — масса вещества, выходящего из элементарного объема в единицу времени; Gхр – скорость расходования исходного вещества в результате химической реакции, протекающей в элементарном объеме:
 (2); (2);  (3). Так как степень превращения равна: (3). Так как степень превращения равна: 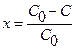 (4); (4); 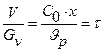 (5); то (5); то  (6), (6), |  Рис.1. Схема реактора идеального смешения. Рис.1. Схема реактора идеального смешения. |
где, 




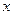
Уравнение (5, 6) представляют собой проектные уравнения реактора идеального смешения и позволяют определить неизвестную величину по заданным. В любом случае для реактора идеального смешения его размер, расход реагентов, начальные и конечные концентрации могут быть определены только при условии, если известна кинетика процесса.
В таблице 1 приведены расчетные уравнения для реактора идеального смешения непрерывного действия при проведении в нем простых обратимых и необратимых, а также сложных химических реакций.
Таблица 1. Расчетные уравнения для РИС-Н
| Схема реакции | Кинетическая модель | Расчетные уравнения |
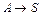 |  |    |
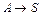 |  при при  | 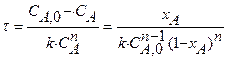 |
 |    |   |
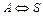 |   |    |
 |    |       |
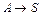  |  |   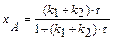 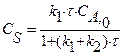  |
Рассмотрим некоторые примеры расчета такого типа реакторов.
Пример 1.
Определить объем реактора идеального смешения для реакции протекающего без изменения объема реакционной массы.
порядок реакции n=1;
объемный расход исходного вещества GV = 0,25 л/мин;
начальная концентрация исходного вещества СА0= 0,5 моль/л;
константа скорости реакции k= 0.15 мин -1 ;
степень превращения xA = 0,52.
Так как реакция первого порядка, скорость реакции определяем по уравнению:

В РИС-Н приравниваем объем реакционной массы к объему реактора, тогда по уравнению:
Пример 2.
Определить объем реактора идеального смешения для обратимой реакции протекающего без изменения объема реакционной массы.
порядок реакции n=2;
объемный расход исходного вещества GV = 4,8 м 3 /ч;
начальная концентрация исходного вещества СА,0= 1,5 кмоль/м 3 ;
константа скорости прямой реакции k1 = 2*10-3 м 3 /(кмоль∙с);
константа равновесия Кр = 9;
требуемая степень превращения xA = 0,8 от равновесной.
Объем реактора, в котором проводится данная реакция, определяем из базового уравнения для РИС-Н:
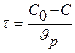

Так как реакция обратимая, составляем кинетическую модель для данной реакции:



С учетом вышеизложенного выражаем время реакции:
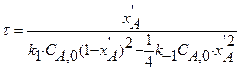
где 

В этом уравнении неизвестными величинами являются фактическая степень превращения и константа скорости обратной реакции. Константу скорости обратимой реакции определяем из уравнения:

Для определения равновесной степени превращения используем константу равновесия, выраженную через концентрации веществ:

где 
Подставляя в данное выражение значения константы равновесия, получаем 

Тогда время реакции будет равно:

С учетом полученного времени реакции объем реактора составит:
Пример 3.
Определить объем реактора смешения и достигаемую степень превращения вещества А при условии, что производительность (П) по продукту R составляет 4,8 кмоль/ч.
объемный расход исходного вещества GV = 100 л/мин.;
начальная концентрация исходного вещества СА0= 1,6 моль/м 3 ;
константа скорости прямой реакции k1 = 0,28 л/(моль*мин.);
константа скорости обратной реакции k2 = 0,12 л/(моль*мин.).
По заданной производительности определяем концентрацию по продукту R. Для этого переведем производительность в моль/мин.
Скорость изменения концентрации продукта R в реакторе смешения можно выразить так:


Из базового уравнения для РИС-Н получаем:

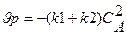
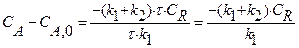

Определяем степень превращения по уравнению:
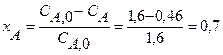
Определяем время пребывания исходя из базового уравнения:
Определяем объем реактора:

Пример 4.
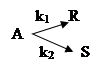
Рассчитать объем реактора смешения для получения максимального количества продукта R, а также определить селективность и производительность по продукту R.
Реакция: А → R → S
объемный расход исходного вещества GV = 18м 3 /ч;
начальная концентрация исходного вещества СА0= 4,8 моль/л;
константа скорости прямой реакции k1 = 5мин -1 и k2 = 1,8мин -1 .
Для получения максимального количества продукта R необходимо выводить реакционную массу из реакционной зоны в момент, когда концентрация вещества R максимальна, что соответствует оптимальному времени пребывания в реакционной зоне.
Из базового уравнения для реактора смешения для продукта R запишем выражение:




Оптимальное время пребывания реакционной массы в зоне реакции определяем по формуле (см. таб.1).
Рассчитываем степень превращения вещества А по формуле (см. таб. 1.):

Определяем концентрацию R на выходе из реактора:

Определяем производительность по продукту R.
Рассчитываем объем реактора смешения:
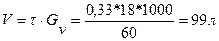
Определяем селективность по продукту R:

Задачи для самостоятельного решения
1. Жидкофазная реакция типа А → 2S имеет константу скорости, равную 4.5 ч -1 .Объемный расход исходного вещества с концентрацией 0.8 моль/л составляет 14,5 м 3 /ч. Рассчитать суточную производительность по продукту R для реактора идеального смешения объемом 3 м 3 .
2. В непрерывном реакторе смешения проводится последовательная реакция типа А→R→S с константами скоростей к1=0,5 ч -1 и к2=0,8 ч -1 . Исходная концентрация вещества А равна 5 кмоль/м 3 . Продукты R и S на входе в реактор отсутствуют. Рассчитать необходимый объем реактора смешения для максимального выхода целевого продукта R, степень превращения исходного реагента, селективность и выход по целевому продукту, если объемный расход составляет 2,4 м 3 /ч.
3. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей к1=0,12 л/(моль/мин) и к2 = 0,8 л/(моль/мин). Объемный поток вещества А равен 3,6 м 3 /ч. Концентрация вещества А на входе в реактор составляет 3,4 моль/л, а степень его превращения – 0,48. Определить концентрации веществ R и S на выходе из реактора и объем реактора смешения.
4. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей к1= 0,24 л/(моль/мин) и к2 = 0,18 л/(моль/мин). Объемный поток вещества А равен 3,6 м 3 /ч. Процесс проводится в реакторе смешения объемом 240 л. Концентрация вещества А на входе в реактор составляет 3,4 моль/л. Определить концентрации всех веществ на выходе из реактора, степень превращения вещества A и селективность по продукту R.
5. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей k1= 0,18 л/(моль/мин) и k2 = 0,06 л/(моль/мин). Объемный поток вещества А равен 40 л/мин. Процесс проводится в реакторе смешения объемом 260 л. Концентрация вещества А равно 2,4 моль/л. Определить производительность реактора по продукту R, степень превращения вещества A и селективность по продукту R.
6. 
с константами скоростей k1= 0,18 л/(моль/мин) и k2 = 0,06 л/(моль/мин). Объемный поток вещества А равен 40 л/мин. Процесс проводится в реакторе смешения объемом 250 л. Концентрация вещества R на выходе из реактора равно 1,2 моль/л. Определить концентрацию вещества А на входе в реактор и степень превращения вещества A.
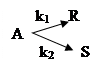
7. 
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Поток вещества поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе смешения объемом 200 л. Степень превращения вещества A составляет 0,8. Определить допустимый расход вещества А.
8. 
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Поток вещества поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе смешения объемом 140 л. Степень превращения вещества A составляет 0,7. Определить производительность реактора по продукту R.
9. 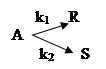
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Процесс проводится в реакторе смешения. Определить объем реактора и достигаемую в нем степень превращения вещества А при условии, что производительность по продукту R составляет 4,8 кмоль/ч.
10. Процесс описывается реакцией типа А + В → R с константой скорости к = 0.28 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,6 моль/л и вещества В с концентрацией 2,0 моль/л равны 100 л/мин. Процесс проводится в реакторе смешения объемом 1,2 м 3 . Концентрация вещества А на входе в реактор составляет 3,4 моль/л. Определить производительность реактора по продукту R.
11. Процесс описывается реакцией типа А + В → R с константой скорости к = 0,54 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,8 моль/л и вещества В с концентрацией 2,7 моль/л равны 100 и 80 л/мин. Производительность реактора по продукту R составляет 8,64 кмоль/ч, концентрация продукта R на выходе — 0,8 моль/л. Определить требуемый объем реактора смешения
12. Процесс описывается реакцией типа 2А → R с константой скорости к = 0,64 л/(моль/мин). Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А -1,8 кмоль/м 3 , производительность реактора по продукту R – 3,8 кмоль/ч. Определить требуемый объем реактора смешения.
13. Процесс описывается реакцией типа А → 2R с константой скорости к = 0,24 мин -1 . Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А — 1,8 кмоль/м 3 , производительность реактора по продукту R – 5,8 кмоль/ч. Определить требуемый объем реактора смешения и объемный расход исходной смеси.
14. Процесс описывается обратимой реакцией первого порядка типа 2А 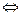
Видео:Химические реакторыСкачать

Химические процессы и реакторы (стр. 8 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |

Следует еще раз обратить внимание на то, что величина (среднее время пребывания реагентов в проточном реакторе, характеризующее для реактора вытеснения продолжительность прохождения потоком расстояния от входа в реактор до некоторой точки z на оси реактора) по физическому смыслу отличается от величины τ в правой части уравнения (5.9) – времени, в течение которого в некоторой фиксированной точке внутри реактора происходит изменение параметров процесса. Условно можно рассматривать как некоторую «внутреннюю» характеристику реактора, непосредственно связанную с его размерами, а τ – как «внешнюю» характеристику, никак не зависящую от конструктивных особенностей реактора.
Говоря о среднем времени пребывания для реактора идеального вытеснения, следует помнить, что в силу первого допущения о плоском профиле линейных скоростей действительное время пребывания всех частиц потока в аппарате будет одинаковым и как раз равным . Однако, для единообразия в дальнейшем для всех проточных реакторов, и в том числе для реактора идеального вытеснения, будем использовать как удобную характеристику, пропорциональную объему реактора.
Уравнение (5.11) для стационарного режима реактора идеального вытеснения можно проинтегрировать относительно :

или, если J – исходный реагент,

Уравнения (5.12), (5.13) по виду напоминают уравнения (5.2), (5.3) для периодического реактора идеального смешения.
Если считать, что элементарный объем dV, для которого составлялся материальный баланс, может двигаться вместе с потоком, в поршневом режиме он может рассматриваться как своеобразный периодический микрореактор идеального смешения, время проведения реакции в котором равно среднему времени пребывания реагентов в реакторе идеального вытеснения.
Уравнения (5.12) и (5.13) могут быть использованы для расчета размеров изотермического реактора идеального вытеснения и глубины протекающего в нем процесса.
Пример 5.2. Определить среднее время пребывания реагентов в проточном реакторе идеального вытеснения для условий примера 5.1 (реакция второго порядка 2А 
Решение. Используем для расчета уравнение (5.13):
Таким образом, для достижения аналогичных результатов значения = V/v для реактора идеального вытеснения (0,4 ч) существенно меньше, чем значение для проточного реактора идеального смешения.
Пример 5.3. Уравнения материального баланса (5.18) и (5.19) могут быть использованы не только для определения среднего времени пребывания и размеров реакционного пространства при заданной глубине химического превращения (проектный расчет). Но и для решения обратной задачи (поверочного расчета) при заданных размерах аппарата для определения реакционного состава на выходе из него.
Приведем примеры аналитического решения математической модели (5.18) и (5.19) для некоторых частных случаев.
Простая элементарная реакция А 
и интегрируем
Тогда
и
Обратимая реакция А 
Подставим это значение w rA в формулу (5.12):
Интеграл может быть записан в таком виде:
Из последнего выражения
или
откуда
Параллельная реакция 
Выражение скорости по компоненту R
Интегрируя левую часть равенства в пределах от c R , 0 до c R и правую – от нуля до (при этом c R , 0 = 0), получим
Аналогично находим
Видео:Основные модели гидродинамики – идеальное вытеснение, идеальное смешение, диффузионная и ячеечнаяСкачать

§ 5.3. Сравнение эффективности проточных реакторов
идеального смешения и идеального вытеснения
Как видно из примеров 5.1 и 5.2, при одинаковых условиях проведения одной и той же реакции для достижения равной глубины превращения среднее время пребывания реагентов в проточном реакторе идеального смешения больше, чем в реакторе идеального вытеснения. Этот факт легко может быть объяснен характером распределения концентрации реагентов по объему указанных реакторов. Если в проточном реакторе идеального смешения концентрации во всех точках равны конечной концентрации (рис. 5.6, линия 1), то в реакторе идеального выяснения в двух соседних точках на оси реактора концентрации реагентов уже отличаются (линия 2). Например, в соответствии с уравнением (5.12) в случае реакции первого порядка (w rA = kс А ) формула распределения концентрации реагента А по длине реактора идеального вытеснения имеет вид
Скорость реакции, согласно закону действующих масс, пропорциональна концентрации реагентов. Следовательно, в реакторе идеального вытеснения она всегда выше, чем в проточном реакторе идеального смешения. А при большей скорости протекания реакции для достижения той же глубины превращения требуется меньшее время пребывания реагентов в реакторе.
Более наглядно эти положения можно проиллюстрировать, сравнивая среднее время пребывания реагентов в проточных реакторах как площади геометрических фигур.
Сравним эффективность работы идеальных проточных реакторов для случая проведения в них простых реакций, не осложненных побочными взаимодействиями. Зададимся одинаковой степенью превращения исходного реагента, и будем считать более эффективным тот реактор, в котором для достижения заданных результатов требуется меньшее среднее время пребывания 
Рис. 5.6. Распределение вдоль оси реактора
концентрации исходного реагента в проточных реакторах
идеального смешения (1) и идеального вытеснения (2)
Для проточного реактора идеального смешения при заданной глубине превращения (концентрации исходного реагента А в выходном потоке с А , f или соответствующей степени превращения х А ,f ) среднее время пребывания τ в соответствии с уравнениями (5.5) и (5.7) можно определить как произведение двух постоянных величин:
т. е. геометрически представить в виде прямоугольника с соответствующими сторонами.
Для стационарного реактора идеального вытеснения
т. е. величина B как определенный интеграл выражается геометрически площадью криволинейной трапеции, ограниченной прямыми c A = c A ,f , c A = c A , 0 , графиком функции l/w rA = f(c A ) и осью абсцисс (см. рис. 5.7, а). Или в соответствии с уравнением (5.7), площадью криволинейной трапеции, ограниченной прямыми х А = 0, х А = x A , f графиком функции l/w rA = f(х А ) и осью абсцисс (см. рис. 5.7, б).
Из рис. 5.7 видно, что площади криволинейных трапеций, соответствующие B , меньше площадей прямоугольников, соответствующих 
Рис. 5.7. Графическое сравнение проточных реакторов идеального смешения и идеального вытеснения как площадей геометрических фигур.
Однако не всегда стремятся к поддержанию более высоких концентраций исходных реагентов. Так, в § 3.3 было показано, что при проведении параллельных реакций разного порядка, в том случае, если порядок целевой реакции меньше порядка побочной реакции (n 1 2 ) , при низких концентрациях исходных реагентов обеспечиваются более высокие значения дифференциальной селективности (см., например, рис. 3.1).
Сравним проточные реакторы идеального вытеснения и идеального смешения при проведении параллельных реакций разного порядка

по выходу целевого продукта R. Будем считать, что в обоих типах реакторов достигается одинаковая степень превращения исходного реагента А (т. е. заранее примем, что B c ).
Выход целевого продукта R для параллельных реакций (I)

[см. уравнение (1.11)].
Достигаемая на выходе из реактора концентрация целевого продукта cR будет определяться, с одной стороны, выбранным типом реактора, а с другой – кинетическими особенностями реакции (I), которые могут быть учтены через дифференциальную селективность φ’, равную отношению скорости расходования реагента А на целевую реакцию к общей скорости его расходования. Для удобства дальнейшего рассмотрения представим систему стехиометрических уравнений (I) в эквивалентном виде:

(это нужно сделать, если стехиометрические коэффициенты а 1 и а 2 не равны). Скорость расходования А на целевую реакцию можно выразить через скорость образования целевого продукта, которая в соответствии с определением скорости [см. уравнение (3.3)] равна
Тогда 
Проинтегрировав дифференциальное уравнение (5.15), получим зависимость концентрации c R от дифференциальной селективности φ‘:
Подставляя выражение для c R в уравнение (5.14), получим

Дифференциальная селективность φ’, стоящая под знаком интеграла, является в общем случае убывающей или возрастающей функцией концентрации исходного реагента А, и в том случае, если концентрация с А не постоянна, для определения Ф R нужно провести интегрирование этой функции. В частности, такую операцию необходимо сделать при расчете выхода продукта R в реакторе идеального вытеснения. Если с А постоянна по объему реактора и во времени (в стационарном реакторе идеального смешения), то и дифференциальная селективность φ’ будет характеризоваться постоянным числовым значением, следовательно, уравнение (5.16) для реактора идеального смешения можно упростить:

Выход целевого продукта Ф R , определенный по уравнениям (5.16) для реактора идеального вытеснения и (5.17) для реактора идеального смешения, можно представить графически в виде площадей криволинейной трапеции (Ф R , B ) и прямоугольника ( ФR,С ). Соотношение между этими площадями зависит от характера функции φ'(c А ).
Если порядок целевой реакции превышает порядок побочной параллельной реакции (n 1 > n 2 ), выход целевого продукта Ф R выше в реакторе идеального вытеснения (рис. 5.8, а). При этом, как указано выше, и среднее время пребывания для достижения заданной степени превращения реагентов меньше, чем в реакторе идеального смешения.
Если порядок целевой реакции меньше порядка побочной реакции (n 1 2 ), более высокое значение выхода целевого продукта достигается в реакторе идеального смешения (рис. 5.8, б). Однако в рассматриваемом случае, т. е. при одинаковой степени превращения исходного реагента, среднее время пребывания cр в реакторе идеального смешения больше, чем в реакторе идеального вытеснения.
Если целевая и побочная реакции имеют одинаковый порядок (n 1 = n 2 ), выход целевого продукта при равной степени превращения исходного реагента не зависит от типа выбранного реактора (рис. 5.8, в).
Рис. 5.8. Графическое сравнение выхода целевого продукта
в проточных реакторах идеального вытеснения (1) и идеального смешения (2) при проведении параллельных реакций разного порядка
Проведенное сравнение показывает, что в ряде случаев для достижения высокого выхода целевого продукта эффективнее реактор идеального вытеснения, а иногда реактор идеального смешения. При этом следует отметить, что даже при достижении более высокого выхода целевого продукта при равной степени превращения реактор идеального смешения имеет больший объем, чем реактор идеального вытеснения.
При сравнении не учитывался ряд факторов, ограничивающих применение аппаратов, работающих в режиме, близком к идеальному вытеснению. К ним следует отнести, например, большое гидравлическое сопротивление трубчатых реакторов, трудность чистки таких аппаратов и т. д. Конструктивно проточные аппараты с интенсивным перемешиванием проще, но обладают тем характерным недостатком, что в них устанавливается низкая концентрация исходного реагента (равная конечной) и, следовательно, низкой будет скорость химической реакции. Для использования преимуществ реакторов смешения и в то же время поддержания в реакционной системе более высоких концентраций реагентов можно создать каскад реакторов идеального смешения последовательным включением нескольких реакторов.
Видео:Реактор ROMM-EH с электрообогревомСкачать

§ 5.4. Каскад реакторов идеального смешения
Каскад представляет собой несколько последовательно соединенных проточных реакторов (секций) идеального смешения (рис. 5.9). Реакционная смесь проходит через все секции. Можно рассматривать в качестве примера такой модели не только систему последовательно расположенных отдельных аппаратов, но и проточный реактор, тем или иным образом разделенный внутри на секции, в каждой из которых осуществляется перемешивание реакционной смеси (рис. 5.10). Например, близка к такому типу аппарата тарельчатая барботажная колонна.
Рис. 5.9. Схема каскада реакторов идеального смешения
Pиc. 5.10. Схема секционного аппарата
с перемешиванием
Для каскада реакторов идеального смешения должны выполняться следующие допущения об идеальности:
· в каждой секции каскада выполняются условия реактора идеального смешения, т. е. мгновенное изменение параметров процесса, равенство параметров во всех точках секции и в потоке, выходящем из нее;
· отсутствие обратного влияния: каждый последующий реактор не влияет на предыдущий.
На рис. 5.11 сравнивается характер изменения концентрации исходного реагента при прохождении реакционной смеси через различные реакторы.
Рис. 5.11. Изменение концентрации реагента при прохождении реакционной смеси через последовательные секции единичного реактора идеального смешения (1), реактора идеального вытеснения (2) и каскада реакторов идеального смешения (3)
Математическая модель каскада реакторов идеального смешения, работающего в изотермическом режиме, представляет собой систему уравнений материального баланса по какому-либо участнику реакции, включающую, по меньшей мере, N уравнений по числу секций каскада.
Уравнения материального баланса для любой секции каскада однотипны. Материальный баланс по компоненту J для i-й секции в стационарном режиме работы каскада имеет вид

[см. уравнение (5.6)] или
где i – среднее время пребывания реакционной смеси в i-й секции;
V – реакционный объем i-й секции; C J, j – 1 – концентрация участника реакции J на входе в i-ю секцию, равная концентрации на выходе из (i–1)-й секции; с J ,i – концентрация компонента J на выходе из i-й секций.
Расчет каскада реакторов идеального смешения обычно сводится к определению числа секций заданного объема, необходимых для достижения определенной глубины превращения, или к определению состава реакционной смеси на выходе из i-й секции каскада.
Допущения об отсутствии обратного влияния в каскаде реакторов идеального смешения существенно упрощают расчет. Он сводится к последовательному решению уравнений материального баланса для каждой секции относительно концентрации реагента (или продукта) на выходе. Выходной параметр для первой секции (концентрация с J , i ), полученный из первого уравнения, является входным параметром для второй секции, выходной параметр второй секции – входным для третьей и т. д.
Различают аналитический метод и численные методы расчета каскада. Применение аналитического метода возможно в том случае, если уравнения материального баланса могут быть аналитически решены относительно концентрации с J . Это можно сделать, например, если протекающие реакции описываются кинетическими уравнениями первого или второго порядка. Рассмотрим определение концентрации реагента А на выходе из каскада реакторов, включающего в себя N секций равного объема (V1 = V2 = . = V i . = V N ) при проведении реакции первого порядка, скорость которой описывается уравнением w rA = kс А . Из уравнения материального баланса для первой секции
Полученное значение с А ,1 подставляем в качестве входной концентрации в уравнение материального баланса для второй секции:
из него определяем
При равенстве объемoв секций 


Продолжая аналогичные расчеты, для N–Pi (последней) секции каскада, получим

Если учесть, что , уравнение (5.19) можно записать в виде
и тогда можно рассчитать число секций заданного объема, необходимых для достижения степени превращения х А :
Если полученное при расчете по уравнению (5.20) N является дробным числом, его округляют в большую сторону для того, чтобы было выполнено условие с А ,N A ,f .
Уравнение (5.20) справедливо, естественно, только для реакции первого порядка.
Для реакций, описываемых кинетическими уравнениями, не позволяющими аналитически решить уравнение (5.18) относительно с (например, реакции дробного порядка), при расчете каскада приходится прибегать к численным методам. Так как уравнения материального баланса для всех реакций однотипны, можно составить алгоритм решения этих уравнений для i-й секции и последовательно применить его N paз.
Наглядным является графический способ расчета каскада реакторов, использующий описанный выше графический метод определения концентрации реагентов на выходе из реактора идеального смешения. Принцип расчета остается прежним. Сначала, графически решая уравнение для первой секции
находят концентрацию с А , 1 (рис. 5.12), построив кинетическую кривую w rA (c A ) и прямую с тангенсом угла наклона (–1/ i ), пересекающую ось абсцисс в точке с А , 0 . Определив с А ,1 , решают уравнение для второй секции:
Для расчета концентрации на выходе из N — го реактора графическое решение повторяют N раз.
Если требуется рассчитать число секций N, необходимое для достижения заданной степени превращения х А , графическое построение продолжают до тех пор, пока абсцисса точки пересечения прямой
Рис. 5.12. Зависимости скорости реакции от концентрации
для расчета каскада реакторов идеального смешения,
состоящего из секций одинакового объема
🌟 Видео
РеакторСкачать

Методика теплогидравлического расчёта активной зоны ЯЭРСкачать

Лекция 28 «Классификация промышленных реакторов»Скачать

Мультифизическое моделирование химических реакторов в COMSOL Multiphysics®. Версия 6.0Скачать

Моделирование химико-технологических процессов. Часть 1. Уровень: базовый.Скачать

ЭнергоТВ - Лекция по теме: «Моделирование теплообменника»Скачать

Лекция 26 «Моделирование гомогенных реакторов проточного типа»Скачать

Ртутный ядерный реакторСкачать

Химический реактор с мешалкой. Принцип работы. Где применяется?Скачать

ВВЭР 1200 - самый мощный реактор | Техногеника | Discovery ChannelСкачать

Проточный реактор высокого давления CFP-HPСкачать

Термоядерный синтез: святой Грааль энергетикиСкачать

Термоядерный реактор: наука о том как скрутить солнце в бубликСкачать

Лабораторный реактор MinniСкачать