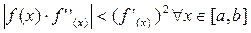Расчетную формулу метода стеффенсена для решения нелинейных уравнений (2 видео)

Нелокальные одношаговые итерационные процессы полного прогноза типа Стеффенсена для решения нелинейных уравнений.

Понятие о разделенных разностях первого и второго порядка для нелинейного оператора. Понятие об одношаговых и многошаговых итерационных процессах. Аналог интерполяционной формулы Ньютона для операторов. Формулировка и доказательство одной из теорем об одношаговом итерационном процессе полного прогноза метода Стеффенсена.

Литература: [14], [15], [16], [17], [20], [21], [22], [23].

21.Нелокальные многошаговые итерационные процессы полного прогноза типа Стеффенсена для решения нелинейных уравнений.

Понятие о разделенных разностях первого и второго порядка для нелинейного оператора. Понятие об одношаговых и многошаговых итерационных процессах. Аналог интерполяционной формулы Ньютона для операторов. Формулировка и доказательство одной из теорем о многошаговом итерационном процессе полного прогноза метода Стеффенсена.

Литература: [14], [15], [16], [17], [20], [21], [22], [23].

22. Нелокальные итерационные процессы неполного прогноза метода хорд для решения нелинейных уравнений с непрерывным нелинейным оператором.
Понятие непрерывного оператора. Разделенные разности первого и второго порядка нелинейного оператора. Аналог интерполяционной формулы Ньютона для операторов. Достоинства и недостатки локального варианта метода хорд. О “полном” и “неполном” прогнозе в итерационных процессах. Формулировка и доказательство одной из теорем о нелокальном итерационном процессе метода хорд с использованием процедуры неполного прогноза.

Литература: [14], [15], [16], [619], [20], [21], [22], [23].

23. Нелокальные итерационные процессы полного прогноза метода хорд для решения нелинейных уравнений с непрерывным нелинейным оператором.

Понятие непрерывного оператора. Разделенные разности первого и второго порядка нелинейного оператора. Аналог интерполяционной формулы Ньютона для операторов. Достоинства и недостатки локального варианта метода хорд. О “полном” и “неполном” прогнозе в итерационных процессах. Формулировка и доказательство одной из теорем о нелокальном итерационном процессе метода хорд с использованием процедуры полного прогноза.

Литература: [14], [15], [16], [19], [20], [21], [22], [23].

24. О методах неполного прогноза, локально сходящихся с кубической скоростью, для решения нелинейных уравнений с гладкими операторами.

Понятие о скорости сходимости итерационных процессов. Понятие “полного” и “неполного” прогнозов. Достоинства и недостатки методов с ускоренной локальной сходимостью. Понятие производной Фреше нелинейного оператора. Формулировка и доказательство теоремы о нелокальной сходимости одного из одношаговых или многошаговых методов нелокального прогноза.

Литература: [14], [15], [16], [19], [20], [21], [23].

25. Об итерационных методах полного прогноза, локально сходящихся с кубической скоростью, для решения нелинейных уравнений с гладкими операторами.
Понятие о скорости сходимости итерационных процессов. Понятие “полного” и “неполного” прогнозов. Понятие о производной Фреше нелинейного оператора. Достоинства и недостатки методов с ускоренной локальной сходимостью. Формулировка и доказательство одной из теорем о нелокальной сходимости одного из одношаговых или многошаговых методов полного прогноза, локально сходящегося с кубической скоростью.

Литература: [14], [15], [16], [19], [20], [21], [23].

26. О нелокальных итерационных методах неполного прогноза, локально сходящихся с кубической скоростью, для решения нелинейных уравнений с непрерывным оператором.
Понятие разделенной разности оператора. О разделенных разностях первого и второго порядка. Аналог интерполяционной формулы Ньютона для операторов. О локальных итерационных процессах третьего порядка. Формулировка и доказательство одной из теорем о нелокальном итерационном процессе неполного прогноза, локально сходящихся с кубической скоростью.

Литература: [14], [15], [19], [20], [21], [22], [23].

27. О нелокальных итерационных методах полного прогноза, локально сходящихся с кубической скоростью, для решения нелинейных уравнений с непрерывным оператором.
Понятие разделенной разности оператора. О разделенных разностях первого и второго порядка. Аналог интерполяционной формулы Ньютона для операторов. О локальных итерационных процессах третьего порядка. Формулировка и доказательство одной из теорем о нелокальном итерационном процессе полного прогноза, локально сходящихся с кубической скоростью.

Литература: [14], [15], [19], [20], [21], [22], [23].

Список литературы

1. Лаврентьев, М. М. О некоторых некорректных задачах математической физики
/ М. М. Лаврентьев. – Новосибирск: Изд-во СО АН СССР, 1962. – 92 с.

2. Тихонов, А. Н. Методы решения некорректных задач / А. Н. Тихонов, В. Я. Арсенин. – М. : Наука, 1979. – 288 с.

3. Вайникко, Г. М. Итерационные процедуры в некорректных задачах / Г. М. Вайникко, А. Ю. Веретенников. – М.: Наука, 1986. – 176 с.

4. Канторович, Л. В. Функциональный анализ в нормированных пространствах / Л. В. Канторович, Г. П. Акилов. – М. : Физматгиз, 1959. – 680с.

5. Савчук, В. Ф. Регуляризация некорректных задач / В. Ф. Савчук, О. В. Матысик. – Брест: Изд-во БрГУ, 2003. – 44 с.

6. Крылов, В. И. Вычислительные методы : учеб. пособие : в 2 ч.
/ В. И. Крылов, В. В. Бобков, П. И. Монастырный. – М. : Наука, 1976. – Ч.1. – 304 с.

7. Вельбицкий, И.В. Технологический комплекс производства программ на машинах ЕС ЭВМ БЭСМ-6 / И.В. Вельбицкий, В.Н. Ходаковский, Л.И, Шолмов. – М.: Статистика, 1980. – 264 с.

8. Вельбицкий, И.В. Формальное задание семантики языков современных систем программирования / И.В. Вельбицкий. – Доклады АН СССР, 1975, т. 223, №6, с. 1329 – 1332.

9. Ван Тассел, Д. Стиль, разработка, эффективность, отладка и испытание программ: пер. с англ. / Д. Ван Тассел – М.: Мир, 1981. – 320 с.

10. Керниган, Б.В. Элементы стиля программирования: пер. с англ. / Б.В. Керниган, Ф.Дж. Плоджер – М.: Радио и связь, 1984. – 160 с.

11. Данилин, А.Р. Структурное программирование (методическая разработка) / А.Р. Данилин – Свердловск, 1981. – 126 с.

12. Хьюз, Дж. Структурный подход к программированию: пер. с англ. / Дж. Хьюз, Дж. Мичтом – М.: Мир, 1980. – 280 с.

13. Лингер, Р. Теория и практика структурного программирования: пер. с англ. / Р. Лингер, Х. Миллс, Б. Уитт – М.: Мир, 1982. – 406 с.

14. Ортега, Дж. Итерационные методы решения нелинейных систем уравнений со многими неизвестными / Дж. Ортега, В. Рейнбоедт. – М.: Мир, 1975. — 558 с.

15. Крылов, В.И. Вычислительные методы высшей математики / В.И. Крылов, В.В. Бобков, П.И. Монастырный. – т. 2, Мн.: Вышэйшая школа, 1975. — 671 с.

16. Полак, М. Численные методы оптимизации. Единый подход / М. Полак. – М.: Мир, 1974. — 376 с.

17. Васильев, Ф.П. Численные методы решения экстремальных задач / Ф.П. Васильев. – М.: Наука, 1980, 518 с.

18. Васильев, Ф.П. Методы решения экстремальных задач / Ф.П. Васильев. – М.: Наука, 1981, 400 с.

19. Дэннис, Дж. Численные методы безусловной оптимизации и решения нелинейных уравнений / Дж. Дэннис, Р Шнабель. – М.: Мир, 1988,

20. Вержбицкий, В.М. Основы численных методов / В.М. Вержбицкий. – М.: Высшая школа, 2002, 848 с.

21. Мадорский, В.М. Квазиньютоновские процессы для решения нелинейных уравнений / В.М. Мадорский. – Брест: 2005, 186 с.

22. Ульм, С.Ю. Об обобщенных разделенных разностях / С.Ю. Ульм. — Изв. АН ЭССР: сер. физ.-мат. н., 1967.- т. 16, № 1. – с. 13-25.

23. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – М.: Бином. Лаборатория знаний, 2006, 636 с.

СОДЕРЖАНИЕ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА. 3

ПЕРЕЧЕНЬ ВОПРОСОВ К ГОСУДАРСТВЕННОМУ ЭКЗАМЕНУ ПО СПЕЦИАЛИЗАЦИИ. 6

СОДЕРЖАНИЕ ВОПРОСОВ К ГОСУДАРСТВЕННОМУ ЭКЗАМЕНУ ПО СПЕЦИАЛИЗАЦИИ. 8

СПИСОК ЛИТЕРАТУРЫ. 15

на учебную программу государственного экзамена по специализации

1-31 03 03-01 «Прикладная математика» для студентов дневной формы обучения математического факультета

Содержание

Фрагмент решения задачи 2.1
Численные методы решения систем нелинейных уравнений
Введение
Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений
Методы решения систем нелинейных уравнений
Выбор модельной функции
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней
Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона
🎥 Видео

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Фрагмент решения задачи 2.1

ЛАБОРАТОРНАЯ РАБОТА № 2.

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: сформировать навыки решения нелинейных уравнений численными методами.

Отчетпо лабораторной работе должен содержать следующие материалы по каждой задаче:

1) постановка задачи;

2) необходимый теоретический материал;

3) результаты вычислительного эксперимента;

4) анализ полученных результатов;

5) графический материал (если необходимо);

6) тексты программ.

Варианты заданий к задачам 2.1-2.10 даны в ПРИЛОЖЕНИИ 2.A.

Основные теоретические сведения

1.1.Пусть задана непрерывная функция f(x) и требуется найти корни уравнения

на всей числовой оси или на некотором интервале .

Всякое значение , удовлетворяющее условию , называется корнем уравнения (1), а способ нахождения этого значения — решением уравнения (1).

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

Уточнение корня – это вычисление интересующего корня с заданной точностью e.

Расчетные формулы методов решения нелинейного уравнения .

Метод дихотомии (половинного деления, бисекций):

x = (a+b)/2 , если ¦(a) ·¦(x)>0 => x * Î [x,b] => a=x, иначе x * Î [a, x] => b=x

Оценка количества итераций n, требуемых для достижения требуемой точности ε (на заданном отрезке [a,b]):

Условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

Метод простых итераций (метод последовательных приближений).

Условие сходимости

Условие завершения итерационного процесса:

Упрощенный метод Ньютона: , n=0,1,…

Условие окончания расчета:

где −корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

Метод ложного положения: , n=0,1,…;

c-фиксированная точка из окрестности корня

Метод секущих: , n=0,1,…

Метод Стеффенсена: , n=0,1,…

Модифицированный метод Ньютона для поиска кратных корней:

, n=0,1,…, m=1,2,…

Индивидуальные задания

Задача 2.1. Даны два уравнения f(x)=0 и g(x)=0. Найти с точностью все корни уравнений, содержащиеся на отрезке [a, b]. Для решения задачи использовать метод бисекции.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Найти аналитическое решение уравнения f(x)=0.

2. Локализовать корни f(x)=0 графически.

3. Найти корни уравнения f(x)=0 с точностью с помощью метода бисекции.

4. Найти корни уравнения f(x)=0 с точностью .

5. Аналогично п. 1-4 попытаться найти корни уравнения g(x)=0. Объяснить полученные результаты.

Фрагмент решения задачи 2.1.

=0, [a,b]=[0,]

Аналитическое решение задачи:

, =1.31811607652818, =1.738244406014586

Численное решение задачи: Локализация корней для численного решения задачи:

(на примере работы пакета MATHCAD)

bisec

Встроенная функция пакета MATHCAD

— задание начального приближения

Значение корня отличается от найденного с помощью функции bisec , так как по умолчанию величина погрешности при работе встроенных функций равна 0.001.

Переопределим параметр для задания погрешности

Значение корня с заданной точностью 1.3181160717.

bisec

Значение корня с заданной точностью 1.7382444060, число итераций 32.

— задание начального приближения

Значения корней в пределах заданной точности совпадают.

Задача 2.2.Найти указанный в варианте корень уравнения f(x)=0 с точностью , двумя способами.

а) Использовать метод бисекции. Предварительно определить отрезок локализации [a, b].

b) Использовать метод Ньютона. В качестве начального приближения для метода Ньютона взять середину отрезка локализации из п. а).

Сравнить число итераций в п. a), b).

Задача 2.3.Локализовать корни уравнения f(x)=0 и найти их с точностью , используя метод простой итерации. К виду x=j(x), удобному для итераций, уравнение f(x)=0 привести двумя способами.

a) Преобразовать уравнение к виду x=x-af(x), где a=2/(M+m), , а x принадлежит отрезку локализации [a, b].

b) Любым другим преобразованием уравнения. Проверить достаточное условие сходимости метода.

Использовать критерий окончания итерационного процесса вида , где в п. a) q=(M-m)/(M+m), в п. b) .

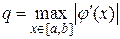
Сравнить число итераций и значения величины q в п. a), b).

Задача 2.4.Локализовать корни уравнения f(x)=0. Найти их с точностью , используя методы простой итерации и Ньютона. Сравнить скорость сходимости методов (по числу итераций).

Задача 2.5.Найти приближенно корень уравнения f(x)=0, принадлежащий отрезку [a,b], с точностью , используя модификацию метода Ньютона для случая кратного корня при значениях m=1,2,3,4,5. По числу итераций определить кратность корня.

Задача 2.6.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Локализовать корни уравнения f(x)=0. Найти их с точностью и , используя метод Ньютона и метод, указанный в индивидуальном варианте. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

Задача 2.7.Локализовать корни уравнения f(x)=0. Найти их с точностью и , используя метод Ньютона, упрощенный метод Ньютона и метод секущих. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

Задача 2.8.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Найти приближенно все (в том числе комплексные) корни уравнения f(x)=0 с точностью , используя метод Ньютона.

УКАЗАНИЕ. Для поиска комплексных корней следует использовать комплексные начальные приближения.

Задача 2.9.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

a)Локализовать корни уравнения f(x)=0. Уточнить их с точностью , используя метод Ньютона. Для поиска кратного корня и определения его кратности следует использовать модификацию метода Ньютона для случая кратного корня с m=1,2,3. При любых ли начальных приближениях такой метод сходится?

b) Рассмотреть уравнение f(x)+d=0, где 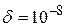. Найти корень кратности 1, используя метод Ньютона. Применить для нахождения кратного корня соответствующую модификацию* метода Ньютона. Удается ли найти кратный корень? Если нет, то использовать метод Ньютона с комплексными начальными приближениями. Сохранился ли кратный корень? Объяснить результаты.

Задача 2.10.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Функция y=f(x) задана неявно уравнением F(x,y)=0. На отрезке [1, 5] построить таблицу значений функции y=f(x) с шагом h=0.5, применяя один из методов численного решения нелинейного уравнения (с точностью ). Построить график функции y=f(x) на заданном отрезке.

ПРИЛОЖЕНИЕ 2.A.

ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 2

Таблица к задаче 2.1

N	f(x)	g(x)	[a, b]
2.1.1
2.1.2
2.1.3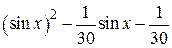
2.1.4
2.1.5
2.1.6
2.1.7.			[5,25]
2.1.8			[0.1,10]
2.1.9			[0.1,2]
2.1.10
2.1.11
2.1.12
2.1.13			[0,3]
2.1.14			[0,2]
2.1.15			[0,3]
2.1.16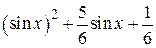
2.1.17
2.1.18
2.1.19
2.1.20
2.1.21
2.1.22			[0.001,3]
2.1.23			[0.1,35]
2.1.24			[0.01,3]
2.1.25
2.1.26			[-0.5,1.5]
2.1.27			[-1.5,0]
2.1.28			[1,3]
2.1.29			[0,3]
2.1.30			[0,5]

Таблица к задаче 2.2 Таблица к задаче 2.3

N	f(x)	Найти корень	N	f(x)
2.2.1		отрицательный	2.3.1
2.2.2		положительный	2.3.2
2.2.3		положительный	2.3.3
2.2.4		наибольший по модулю	2.3.4
2.2.5		все корни	2.3.5

Таблица к задаче 2.4

f(x)
N
2.4.1	4.545004	-3.055105	-18.06895	4.002429	4.722482
2.4.2	-2.656764	-3.406111	10.89372	-1.752935	-3.423612
2.4.3	-4.556062	2.93309	9.274868	-10.32081	0.422098
2.4.4	7.809249	16.28542	-2.771356	-27.95304	-11.33921
2.4.5	-13.0072	60.24546	-122.0716	105.6798	-30.19201

Таблица к задаче 2.5

N	f(x)	[a, b]
2.5.1		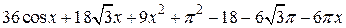[0.8,1.2]
2.5.2		[0.3,0.7]
2.5.3		[0.5,1]
2.5.4		[0,1]
2.5.5		[0,0.7]

Таблица к задаче 2.6 Таблица к задаче 2.7

N	f(x)	Метод*	N	f(x)
2.6.1		упрощенный метод Ньютона	2.7.1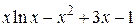
2.6.2		метод ложного положения	2.7.2
2.6.3		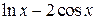метод простой итерации	2.7.3
2.6.4		метод секущих	2.7.4
2.6.5		метод Стеффенсена	2.7.5

Таблица к задаче 2.8 Таблица к задаче 2.9

N	f(x)	N	f(x)
2.8.1		2.9.1
2.8.2		2.9.2
2.8.3		2.9.3
2.8.4		2.9.4
2.8.5		2.9.5

Таблица к задаче 2.10

N	F(x,y)
2.10.1	, ,
2.10.2	, ,
2.10.3	, ,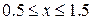
2.10.4	, ,
2.10.5	, ,

Контрольные вопросы

1. Опишите этапы численного решения уравнений

2. Опишите схему алгоритма отделения корней

3. Перечислите алгоритмы уточнения корней уравнения

4. Опишите методы уточнения корней уравнения

5. Опишите схему алгоритма метода бисекций (дихотомии)

6. Как рассчитать количество итераций n, требуемых для достижения требуемой точности ε

7. Объясните алгоритм решения нелинейного уравнения методом
простых итераций

8. Объясните схему алгоритма метода Ньютона

9. Объясните формулы итерационных процессов численного решения уравнений

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.

Видео:10 Численные методы решения нелинейных уравненийСкачать

Численные методы решения систем нелинейных уравнений

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

method:
hybr -используется модификация Пауэлл гибридный метод;
lm – решает системы нелинейных уравнений методом наименьших квадратов.
Как следует из документации [3] методы broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylov являются точными методами Ньютона. Остальные параметры являются «не обязательными» и с ними можно ознакомится в документации.

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

Определим матрицу Якоби:

(4)

Запишем(3) в виде:

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Решение для n=100:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Решение для n=100:

Решение для n=200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Получим:
Solution:
[ 0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500