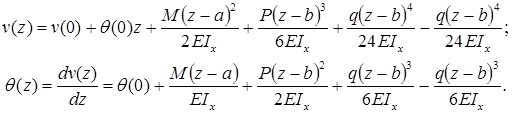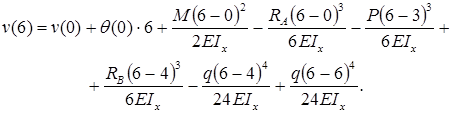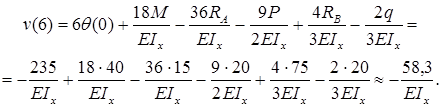Расчет статически неопределимых балок с помощью дифференциального уравнения изогнутой оси (8 видео)

Метод начальных параметров

Продифференцировав два раза уравнение (9.1) при EJ = const и использовав дифференциальные зависимости (7.6) при изгибе, получим

Последнее выражение является дифференциальным уравнением изогнутой оси балки четвертого порядка

устанавливающим дифференциальную зависимость между прогибом и распределенной поперечной нагрузкой. При отсутствии последней уравнение (9.7) становится однородным:

Проинтегрируем уравнение (9.8). С учетом выражений (9.6) получим

Введем в начальном сечении балки при х = 0 следующие четыре величины:

Эти величины представляют собой значения прогиба, угла поворота, изгибающего момента и поперечной силы в начальном сечении балки (рис. 9.8), причем и₀ и (р₀ называются кинематическими начальными параметрами, а М₀ и Q₀ — статическими начальными параметрами.

Выразим постоянные интегрирования С_р С₂, С₃ и С₄ в решениях (9.9) через начальные параметры. Положив в этих выражениях х = 0, получим

Подставив постоянные в последнее выражение из (9.9), получим решение однородного дифференциального уравнения изогнутой оси балки (9.8) в форме метода начальных параметров:

Продифференцировав уравнение (9.12), получим выражения для угла поворота и внутренних усилий в балке:

Отметим, что внутренние усилия М и Q не зависят от кинематических начальных параметров l> ₀ и ср₀.

Выражения (9.12) и (9.13) полностью определяют напряженное и деформированное состояния балки в том случае, когда распределенная поперечная нагрузка отсутствует, а функции и(х), ср(х), М(х) и Q(x) являются непрерывными. Рассмотрим случаи, когда эти функции имеют разрывы, и покажем, как учесть их влияние.

Внутренние усилия Q и М имеют скачки (разрывы) в сечениях, где приложены сосредоточенные силы и моменты. У кинематических величин ср и v разрывы отражают наличие промежуточных шарниров и так называемых параллелограммных механизмов.

В промежуточном шарнире изогнутая ось балки может иметь излом, что характеризует взаимный поворот Дф поперечных сечений (рис. 9.9). Следовательно, можно записать: х — а, п_пр = 1>_лев;

Параллелограммный механизм допускает взаимное поперечное смещение Av (рис. 9.10), а углы поворота сечений остаются одинаковыми. Это позволяет записать: x = a,v = v _а + Av; ф = ф .

5 пр лев 5 *пр г лев

Если в каком-либо сечении балки х — а имеет место разрыв одной из четырех величин и, ф, М и Q, то он может оказать влияние на эти величины в сеченияхх > а. Для учета влияния разрывов можно воспользоваться методом наложения, вытекающим из принципа независимости действия сил. При этом к выражению (9.12) надо добавить член, равный произведению величины разрыва на функцию при соответствующем начальном параметре, вычисляемую для разности х — а.

Рассмотрим, например, действие сосредоточенной силы Р (рис. 9.11). В этом случае в сечении х = а функции и(х), (р(х) и М<х) остаются непрерывными, а поперечная сила Q имеет разрыв (скачок) на величину Р, то есть можно записать:

На первом участке балки прогиб зависит только от начальных параметров и определяется выражением (9.12). На втором участке к этому выражению надо добавить функцию v*(x), отражающую влияние разрыва AQ на прогиб балки за сечением х = а:

Таким образом, прогиб балки на первом и втором участках определяется по формуле

где, как и ранее, вертикальная черта с цифрой внизу соответствует границе участков (см. пример 9.2).

Аналогично можно учесть влияние на прогиб балки и других сосредоточенных факторов — сосредоточенного момента М и скачков угла поворота Д(р и прогиба Av.

Для учета влияния распределенной поперечной нагрузки ее надо представить как бесконечное множество элементарных сосредоточенных сил dP = q(t) dt (рис. 9.12), где t — новая переменная, изменяющаяся в пределахa Ь

Первый член в формуле (9.17) соответствует равномерно распределенной нагрузке, условно продолженной до конца балки. Второй член соответствует компенсирующей нагрузке на участке х > Ь, направленной в противоположную сторону. На рис. 9.13 эти взаимно уравновешенные нагрузки показаны пунктиром.

Аналогичным образом можно учесть влияние поперечной нагрузки, распределенной по линейному закону, распределенной моментной нагрузки и т.п. Функции, добавляемые к выражению для прогиба (9.12) для учета влияния наиболее распространенных статических и кинематических воздействий на балку, приведены в табл. 9.1.

Расчет статически неопределимых балок с помощью дифференциального уравнения изогнутой оси

С помощью данных табл. 9.1 запишем уравнение изогнутой оси балки с учетом начальных параметров и наиболее распространенных воздействий (рис. 9.14):

Формула (9.18) является аналитическим выражением для прогиба балки на всех показанных на рис. 9.14 участках, границы которых обозначены вертикальной чертой с номером участка. На первом участке выражение для прогиба ограничено вертикальной чертой с цифрой 1, на втором участке — вертикальной чертой с цифрой 2 и т.д. Если нагрузки имеют другое направление, чем на рис. 9.14, то у соответствующих функций в выражении (9.18) надо поменять знак на противоположный. При наличии нескольких однотипных воздействий (например, нескольких сосредоточенных сил и т.п.) в уравнение изогнутой оси надо ввести такое же количество соответствующих функций.

Продифференцировав уравнение изогнутой оси (9.18), можно записать выражение для углов поворота ср(х).

Получить уравнение изогнутой оси балки в форме метода начальных параметров можно также на основании дифференциального уравнения второго порядка (9.1). Для этого надо записать выражение для изгибающих моментов в произвольном сечении балки с учетом влияния статических начальных параметров М₀ и Q₀ и заданных нагрузок и произвести интегрирование.

Рассмотрим, например, балку, нагруженную распределенной нагрузкой, изменяющейся по линейному закону (рис. 9.15). Изгибающий момент в сечении х равен

где

Подставим это выражение в дифференциальное уравнение (9.1) и выполним интегрирование:

Положив в этих решениях х = О, выразим постоянные интегрирования Cj и С₂ через кинематические начальные параметры v_Q и ф₀:

Подставим С, и С₂ в полученное выше выражение для прогиба в пределах первого участка балки. Тогда получим

Это выражение является частным случаем уравнения (9.18). Учет влияния сосредоточенных воздействий, как и ранее, может быть произведен с помощью метода наложения.

Входящие в выражение (9.18) начальные параметры i>₀, ₀ = 0; М₀ = 0; С?₀ = R_A. Неизвестный начальный параметр ф₀ подлежит определению из граничного условиях = l,v = 0.

3. Свободный конец в начальном сечении (рис. 9.18).

В начале расчета известны два начальных параметра: М₀ = —М Q₀ = 0. Для определения о₀ и ф₀ можно использовать два граничных условия: х = а, о = 0; х = а + I, о = 0.

4. Балка с промежуточным шарниром (рис. 9.19).

В начальном сечении имеем: о₀ = 0; М₀= 0; Q₀ = R_A. Неизвестные величины ф₀ и Дф_д подлежат определению из граничных условий в заделке: х = / + а о = 0, ф = 0.

5. Статически неопределимая балка (рис. 9.20).

Для статически неопределимых балок предварительный статический расчет невозможен, так как число искомых статических величин превышает число уравнений равновесия, которые можно составить для их определения. Следовательно, в начале расчета таких балок могут быть неизвестны как кинематические, так и статические начальные параметры. Неизвестные величины подлежат определению из кинематических и статических граничных условий. Последние ставятся относительно изгибающих моментов и поперечных сил.

Например, балка на рис. 9.20 статически неопределима, поскольку трех уравнений равновесия недостаточно для определения четырех опорных реакций. В начальном сечении балки имеем: п₀ = 0; ф₀ = 0. Для определения неизвестных начальных параметров M_Q и Q₀ можно использовать следующие граничные условия: х = I; и = 0; М = М (смешанные граничные условия).

Использовав граничные условия, можно получить необходимое число уравнений относительно всех неизвестных величин. После их определения можно с помощью уравнения (9.18) записать окончательные выражения для прогибов и углов поворота в балке, а для статически неопределимых балок — построить также эпюры (9 и М.

Вычислив значения v и ср в характерных сечениях балки, можно построить эпюры этих величин. Для правильного построения и контроля эпюр Q, М, ср и v надо использовать дифференциальные соотношения при изгибе:

Соотношения (9.19), а также характер внешней нагрузки позволяют установить наличие особенностей в эпюрах Q, М, ф и и, а именно скачков, изломов, экстремумов и точек перегиба (см. § 7.4). Рассмотрим примеры использования метода начальных параметров.

Пример 9.3. Для балки с промежуточным шарниром (рис. 9.21, а) запишем с помощью метода начальных параметров выражения для ф и v, вычислим значения этих величин в характерных сечениях и построим эпюры Q, М, ф и и.

Данная балка статически определима. Ее можно представить состоящей из несущей и несомой частей (балок), соответственно ВС и АВ. Определим значение опорной реакции R_A и построим эпюры изгибающих моментов и поперечных сил:

Эпюры Q и М приведены на рис. 9.21, б, в. Начальные параметры равны

Учитывая значения начальных параметров и характер нагрузки, запишем с помощью уравнения (9.18) выражения для прогибов и углов поворота в пределах трех характерных участков балки:

В этих выражениях неизвестными величинами являются начальный параметр ср₀ и взаимный угол поворота Аср₅ в промежуточном шарнире. Для их определения используем граничные условия в заделке С:

Получили систему двух уравнений относительно неизвестных величин ср₀ и Д(р_в:

решив которую находим

Запишем окончательные выражения для v и (р и вычислим значения этих величин в характерных сечениях балки:

Построим эпюры v и ср и отметим их особенности на основании дифференциальных соотношений (9.19).

Эпюра ср в сечении х = 4м (промежуточный шарнир) имеет скачок (разрыв). В сечении под сосредоточенной силой на эпюре ф имеет место точка перегиба (смена знака кривизны), поскольку в этом сечении изменяется знак поперечной силы. В сеченияхх = О и х = 4 м касательные к эпюре ф параллельны оси, поскольку в этих сечениях изгибающий момент равен нулю. В пределах второго участка изменяется знак угла поворота. Определим координату сечения х₀ где угол поворота обращается в нуль:

На эпюре v в сечении В имеют место излом и смена знака кривизны. В сечении С (заделка) касательная к эпюре v совпадает с осью балки, поскольку в этом сечении ф = 0. В сечении х =х₀ прогиб имеет экстремум, значение которого равно

Эпюры v и ф приведены на рис. 9.21, г, д.

Пример 9.4. Для балки на рис. 9.22, а построим эпюры Q и М и вычислим значение прогиба в сечении, где приложен сосредоточенный момент.

Данная балка статически неопределима, поскольку для определения четырех опорных реакций R_a, Н_а, М _а и R_b можно составить только три уравнения равновесия.

В начальном сечении балки имеем: и₀ =0; ср₀ = 0; M_Q = М_А, Q₀ = R_a Запишем с помощью (9.18) выражение для прогиба в пределах двух характерных участков:

Для определения неизвестных статических начальных параметров М₀ и Q₀ используем граничные условия на опоре В:

Решая систему двух уравнений

находим значения статических начальных параметров:

Изгибающий момент M_Q вызывает растяжение верхних волокон балки (его направление показано на рис. 9.22, а пунктиром). Дальнейший статический расчет балки прост и не требует пояснений.

Определим экстремальное значение изгибающего момента на втором участке:

Эпюры Q и М приведены на рис. 9.22, б, в. Прогиб балки в сечении, где приложен сосредоточенный момент, равен

В заключение приведем формулы для прогибов и углов поворота в консольных и шарнирно-опертых балках при простых нагрузках (табл. 9.2).

Содержание

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
Уравнение упругой линии балки на примере
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Определение перемещений методом интегрирования дифференциального уравнения оси балки
📽️ Видео

Видео:Сопротивление материалов. Занятие 10. Часть 1. Расчет статически неопределимой балки.Скачать

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

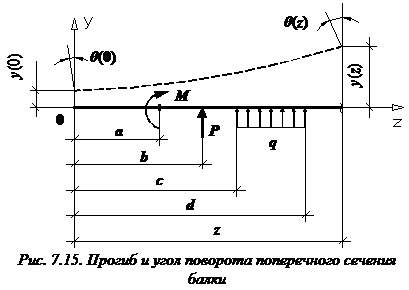
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 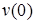и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

Уравнение упругой линии балки на примере

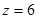
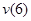
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .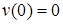

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

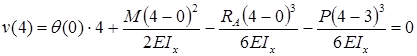
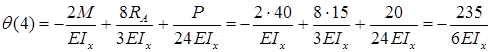
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

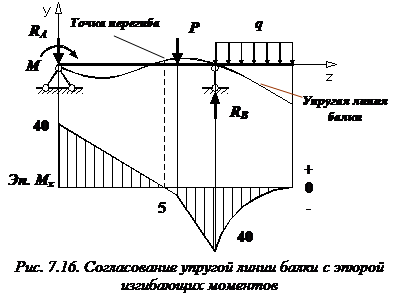
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

ПроСопромат.ру

Видео:30. Статически неопределимая балка ( уравнение трех моментов ) ( практический курс по сопромату )Скачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Статически неопределимая балка ( 1 раз ). СопроматСкачать

Определение перемещений методом интегрирования дифференциального уравнения оси балки

Для балки определить максимальный прогиб и максимальный угол поворота.

Ввиду симметрии нагрузки опорные реакции А=В=ql/2

Дифференциальное уравнение изогнутой оси балки:

Интегрируем данное уравнение дважды. После первого интегрирования получаем уравнение углов поворота:

(а)

После второго интегрирования получаем уравнение прогибов:

(б)

Необходимо определить значение постоянных интегрирования — С и Д. Определим их из граничных условий. В сечениях А и В балка имеет шарнирные опоры, значит прогибы в них равны нулю. Следовательно, имеем граничные условия:

1) z = 0, y = 0.

Используем первое граничное условие: z = 0, y = 0.

Тогда из (б) имеем: