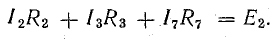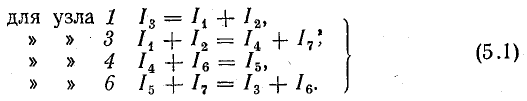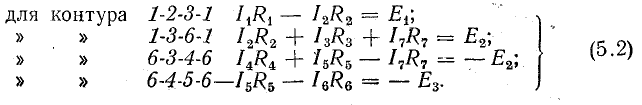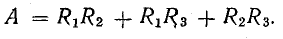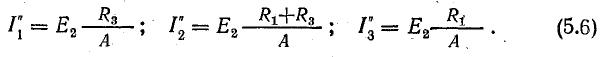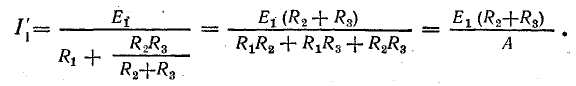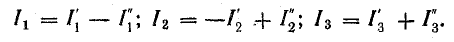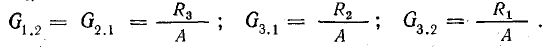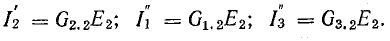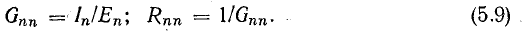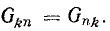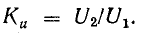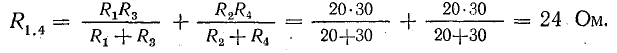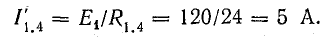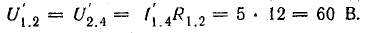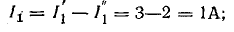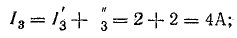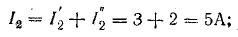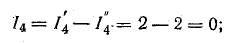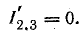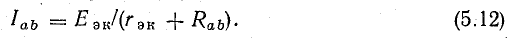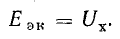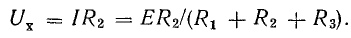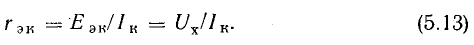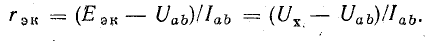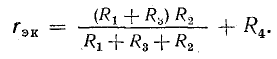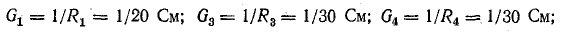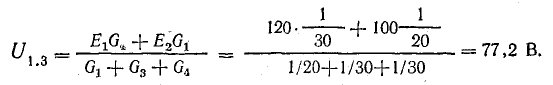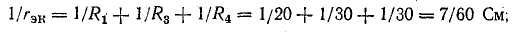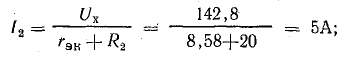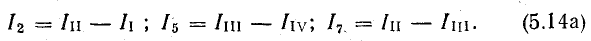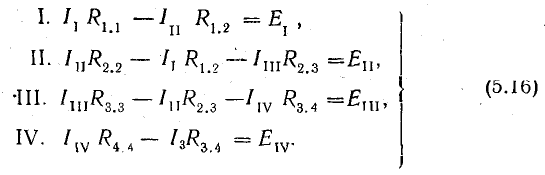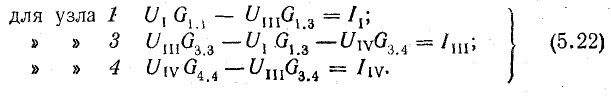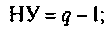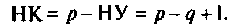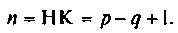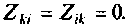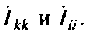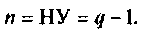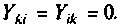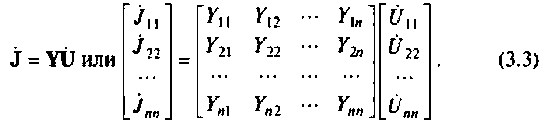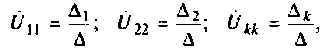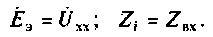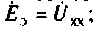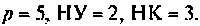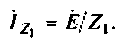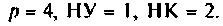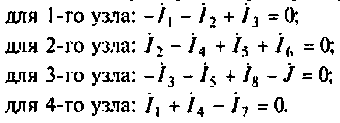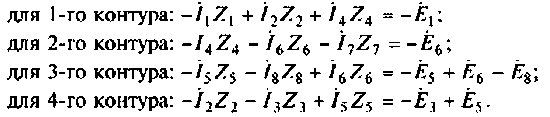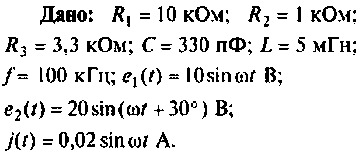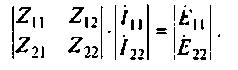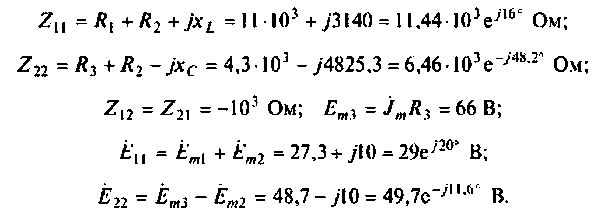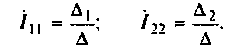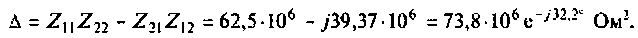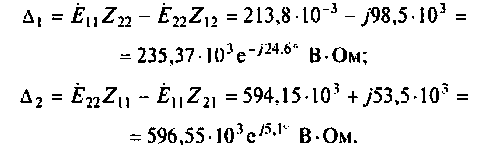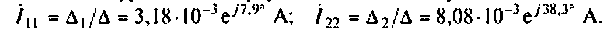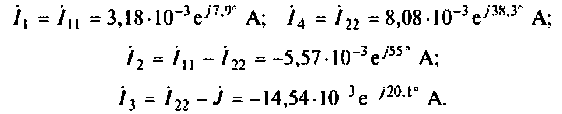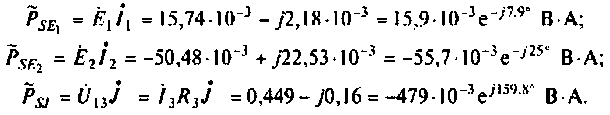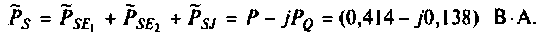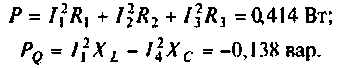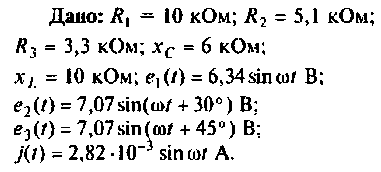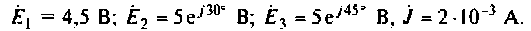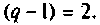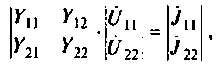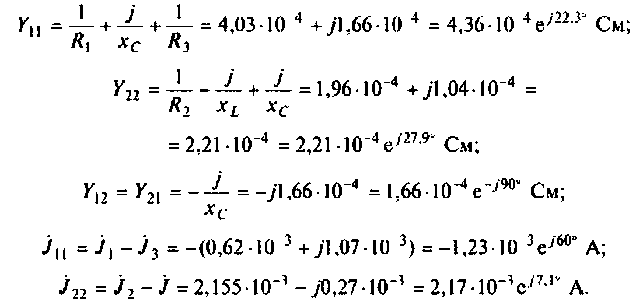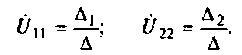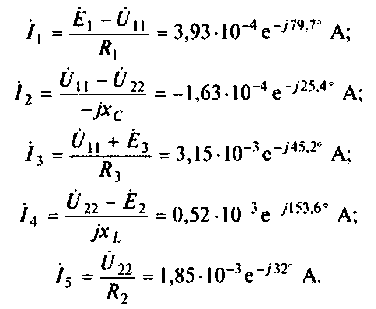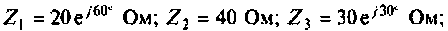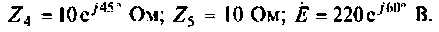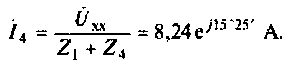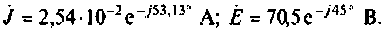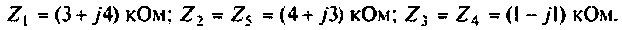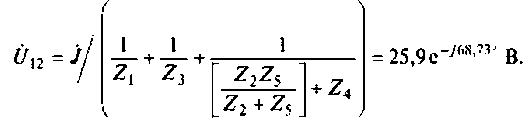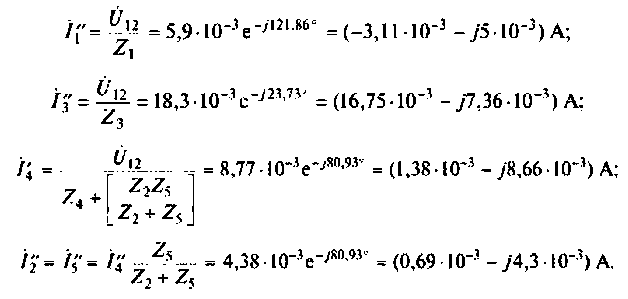Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.
- Порядок расчёта:
- Метод узловых и контурных уравнений
- Алгоритм расчета электрической цепи методом контурных и узловых уравнений
- Готовые работы на аналогичную тему
- Примеры расчета методом узловых и контурных уравнений
- Методы анализа сложных электрических цепей
- Некоторые методы анализа сложных электрических цепей
- Метод узловых и контурных уравнений
- Обоснование метода
- Узловые уравнения
- Контурные уравнения
- Метод наложения токов
- Обоснование метода
- Порядок расчета
- Входные и взаимные проводимости и сопротивления
- Коэффициенты передачи напряжения и тока
- Метод эквивалентного генератора
- Обоснование метода
- Определение э.д.с. и внутреннего сопротивления эквивалентного генератора
- Метод контурных токов
- Контурные токи и э.д.с.
- Собственные и общие сопротивления контуров
- Метод контурных токов
- Метод узловых напряжения
- Узловые напряжения и токи
- Узловые и общие проводимости
- Метод узловых напряжений
- Методы расчета сложных электрических цепей
- Анализ структуры электрической цепи
- Расчет электрических цепей методом уравнений Кирхгофа
- Расчет электрических цепей методом контурных токов
- Расчет электрических цепей методом узловых напряжений
- Расчет электрических цепей методом наложения
- Расчет цепей методом эквивалентного генератора
- Примеры решения задач
- 🎦 Видео
Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Порядок расчёта:
1. Произвольно задаёмся направлением токов в ветвях.
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.
Красным выделены изменения после первого действия
Синим выделены изменения после третьего пункта
2. Используя первый закон Кирхгофа составим уравнения для (n-1) узлов схемы. Где n – число узлов. То есть для схемы с четырьмя узлами, составляем три уравнения. Для этого:
- Обозначаем узлы буквами.
- Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус.
0=I1-I4-I6 (Полученное уравнение) - Повторяем пункт B ещё для двух узлов.
0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
3. Используя второй закон Кирхгофа составим уравнения для каждого контура схемы. Для этого произвольно зададимся направлением обхода контура (по часовой или против часовой). Для контура ABDA направление обхода контура выберем по часовой стрелке.
3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)
3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)
3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.
Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3
Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5
Контур ABCA 0=I6*R6-I4*R4+I5*R5
4. Решаем полученную систему уравнений и находим величины токов во всех ветвях.
Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.
Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.
I3=I1+I2(Узел D)
I5=I3-I4(Узел В)
I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:
Заменим токи I3 I5 I6 и получим уравнения с тремя токами :
Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:
40 = 71*I1 + 24*I2 + 14*I4
20 = 55*I1 + 93*I2 — 61*I4
0 = 60*I1 + 16*I2 — 81*I4
Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.
Правильность решения можно проверить с помощью баланса мощностей.
Видео:Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
Метод узловых и контурных уравнений
Вы будете перенаправлены на Автор24
Видео:Метод узловых и контурных уравненийСкачать

Алгоритм расчета электрической цепи методом контурных и узловых уравнений
Метод узловых и контурных уравнений — самый простой метод расчета электрической цепи, который основан на составлении уравнений по первому и второму законам Кирхгофа.
Первый закон Кирхгофа звучит следующим образом: алгебраическая сумма токов в ветвях цепи, которые сходятся в каждом узле, равна нулю. При этом ток, направленный к узлу считается положительным, а направленный от него отрицательным. Сумма токов, которые направлены к узлу цепи равняется сумме токов, направленных от него. Таким образом получается, что в узел втекает столько же тока, сколько и вытекает из него (правило фундаментального закона сохранения заряда.
Второй закон Кирхгофа гласит — алгебраическая сумма напряжений на резистивных составляющих замкнутого контура цепи равняется сумме электродвижущих сил в составе данного контура. В том случае, когда источник электродвижущей силы отсутствует в контуре, суммарное падение напряжений равно нулю.
Порядок расчета электрической цепи методом узловых и контурных уравнений выглядит следующим образом:
- Определяют количество неизвестных токов (количество ветвей цепи равняется число токов в ней).
- Произвольно выбираются направление определенных токов и обозначаются на рассматриваемой схеме.
- Составляется система уравнений согласно первому закону Кирхгофа, количество которых на единицу меньше количества узлов в рассматриваемой схеме.
- Составляются недостающие, до общего количества, уравнения по второму закону Кирхгофа. Направления обхода тока, как правило, выбираются одинаковыми.
- Определяются неизвестные токи, после чего решается получившаяся система уравнений. В том случае, когда рассчитанный (определенный) ток имеет отрицательную величину, это значит, что его направление противоположно направлению, которое было выбрано в пункте 2.
- Осуществляется проверка посредством составления баланса мощностей или расчет рассматриваемой цепи производится другим методом.
Готовые работы на аналогичную тему
Баланс мощностей электрической цепи — это суммарная генерируемая источниками электроэнергии мощность, равная сумме мощностей, которые потребляются в цепи.
Видео:Законы Кирхгофа. Метод контурных токов (МКТ)Скачать

Примеры расчета методом узловых и контурных уравнений
Рассмотрим схему, которая представлена на рисунке ниже
Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ
Допустим, что E1 = 50 В; Е2 = 30 В; Е3=3 В; R1 = 100 Ом; R2 = 50 Ом; R3 = 8 Ом; r03 = 0,5 Ом; r01 = r02 = 0 Ом. Нам необходимо рассчитать все токи цепи.
Решение задачи следует начинать с определения количества неизвестных токов и выбора их направления. В каждом неразветвленном участке цепи (ветвь) электрический ток одно и тоже значение от его начала и до конца. К узловым точкам (А и Б) присоединены три ветви:
- БВГА с током I1
- БА с током I2
- БДЖА с током I3
Таким образом количество разных токов равняется количеству ветвей рассматриваемой цепи. Направление токов выбирается произвольно и при них составляются уравнения. После чего они решаются и определяются их истинные направления (по алгебраическим знакам). В рассматриваемой задаче три неизвестны — I1, I2, I3, для них и составляется система уравнения по законам Кирхгофа. Уравнения на основе первого закона более простые, поэтому следует начинать с них. Известно, что для электрической цепи с n узлами можно составить n-1 независимых уравнений. Уравнение по первому закону Кирхгофа для узла А будет выглядеть следующим образом:
Уравнения, которых не хватает составляются по второму закону Кирхгофа. Для этого выбираем контуры БАЖДБ и ВГЖДВ. Принимаем, что обход контуров цепи осуществляется по часовой стрелке и учитывая правила знаков получаем следующие уравнения:
Подставив численные значения в третьем уравнение получаем:
$I1*(100+0) – I3*(8+0,5) = 50-30$
Таким образом вычисление токов сводится к решению системы из трех уравнений с тремя неизвестными. Рассчитаем I2 из уравнения и подставим значение в уравнение:
$-50*(I1+I3) – 8,5*I3 = 27$
Приводя подобные числа получим:
В результате у нас получилось два уравнения с двумя неизвестными (I1, I3). Уравнение (-50I1-58,5I3 = 27) умножается на два, в результате чего получается:
$-100*I1- 117*I3 = 54$ Получившееся уравнение складывается с уравнение (100I1-8,5I3 = 20):
$I3 = — (64/125,5) =- 0,5 A$
Теперь подставляем получившееся значение I3 в уравнение, где неизвестно I1:
$I1 = -24,5/-100 = 0,245A$
Теперь получившиеся значения подставляются в первое уравнение, составленное по первому закону Кирхгофа:
$I2 = 0,245+0,5 = 0,745A$
Проверка результата осуществляет при помощи составления баланса мощностей или решения задачи другим способом.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 08 2021
Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет
Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Методы анализа сложных электрических цепей
Содержание:
Методы анализа сложных электрических цепей:
Электрические цепи, которые не являются параллельно-последовательными, называются сложными. Для анализа сложных цепей используются прямые методы: метод узловых напряжений и метод контурных токов. Изучение указанных методов для простоты будет проводиться на примере резистивных цепей, что не утратит общности получаемых результатов.
Видео:46 Алгоритм решения метода узловых и контурных уравненийСкачать

Некоторые методы анализа сложных электрических цепей
Анализом электрических цепей называют определение токов (или напряжений) в ее ветвях.
Был рассмотрен расчет только относительно простых электрических цепей. В расчетах цепей сложной конфигурации с несколькими источниками энергии рассмотренные ранее методы применяются для отдельных простых участков, если имеются необходимые исходные данные.
В общих же случаях применяются другие методы, основой которых служат законы Кирхгофа.
Метод узловых и контурных уравнений
Методы анализа с применением законов Кирхгофа позволяют рассчитать электрическую цепь любой конфигурации и сложности, т. е. являются основными.
Обоснование метода
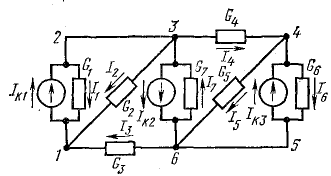
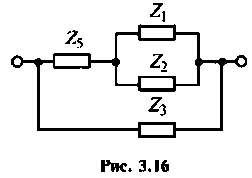
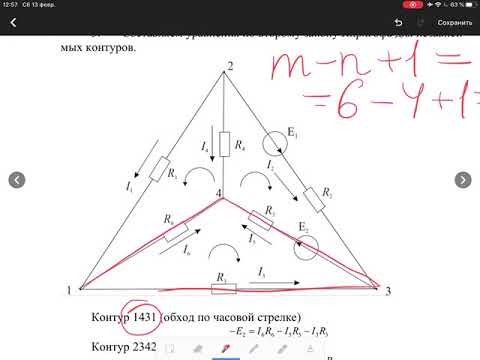
Рассматривая схему любой разветвленной электрической цепи, можно отметить в ней электрические узлы и выделить контуры. Например, в схеме рис. 3.16 имеется четыре узла (точки 1, 3, 4, 6) и несколько контуров (1-2-3-1; 1-3-6-1 и др.).
Для каждой узловой точки можно составить уравнения токов по первому закону Кирхгофа (узловые уравнения), например, для узла 3 I1 + I2 = I4 + I7 для каждого контура — уравнение напряжений по второму закону Кирхгофа (контурные уравнения), например для контура 1-3-6-1
В эти уравнения входят токи в ветвях, определение которых составляет ближайшую цель расчета, которая достигается совместным решением системы узловых и контурных уравнений; их число должно быть равно числу неизвестных токов.
Прежде чем приступить к составлению уравнений по законам Кирхгофа, необходимо выбрать условно-положительное направление тока в каждой ветви (число неизвестных токов, как нетрудно видеть, равно числу ветвей).
Положительные направления токов выбирают произвольно. Действительные направления токов могут не совпадать с условно-положительными. Ошибка в выборе направления тока в результате решения будет обнаружена: ток с неправильно выбранным направлением получится отрицательным. Изменив его направление, в дальнейших расчетах можно считать его положительным.
Узловые уравнения
Запишем систему узловых уравнений для рассматриваемой схемы
В этой системе уравнений любые три уравнения являются независимыми, так как в каждое из них входит хотя бы один новый ток по сравнению с другими уравнениями.
Четвертое уравнение не содержит нового тока, поэтому его можно получить из предыдущих трех несложными подстановками.
При наличии в схеме n узлов можно составить по первому закону Кирхгофа n — 1 независимых уравнений.
Число независимых уравнений, составленных по первому закону Кирхгофа, недостаточно для определения всех неизвестных токов.
В схеме рис. 3.16 насчитывается семь неизвестных токов, а независимых узловых уравнений только три. Еще четыре уравнения составим по второму закону Кирхгофа.
Контурные уравнения
Из всех контуров схемы выбирают те, для которых можно составить наиболее простые независимые уравнения.
При этом можно руководствоваться таким правилом: каждое после-дующее уравнение будет независимо от предыдущих, если в данный контур входит хотя бы одна ветвь схемы, которая не входила в уже использованные контуры.
Можно доказать, что число независимых контурных уравнений для схемы, содержащей m ветвей и n узлов, составляет m — n + 1.
Для десяти контуров при m = 7 в данном случае независимых контурных уравнений можно составить четыре, т. е. столько, сколько необходимо для определения всех токов:
Правильность определения токов в цепи можно проверить, подставив их найденные величины в одно из уравнений, которые составлены для схемы этой цепи, но не вошли в систему уравнений, взятых для решения. С этой же целью можно составить баланс мощностей цепи.
Метод наложения токов
В некоторых случаях расчет электрических цепей можно провести относительно просто, используя принцип наложения.
Этот принцип применяется только к линейным системам, а в данном случае — для расчета линейных электрических цепей.
Обоснование метода
Рассмотрим в качестве примера схему рис. 5.1, а и составим для нее систему уравнений по законам Кирхгофа: 
Ток каждой ветви из этой системы линейных уравнений-определяется однозначно.
Решение системы (5.3) дает выражения для токов:
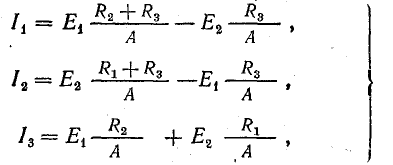
где
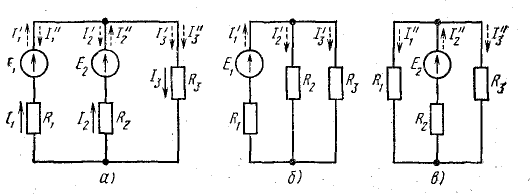
Рис. 5.1. К методу наложения токов
Как и следовало ожидать, величины токов определяются действием всех э. д. с., имеющихся в схеме, т. е. каждая э. д. с. вносит в величину тока каждой ветви свою определенную долю. Предположим, что в схеме действует только э. д. с. Е1, а Е2 = 0. Тогда получим величины токов, вызываемых э. д. с. Е1: 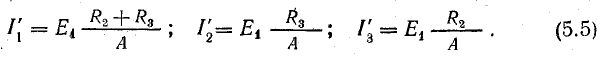
Полагая Е1 =0, получим величины частных токов от действия э. д. с. Е2:
Для любой схемы с линейными элементами можно провести подобные рассуждения, из которых следует метод расчета электрических цепей: определяются частные токи в ветвях от действия каждой э. д. с.; действительный ток каждой ветви равен алгебраической сумме частных токов этой ветви: 
где Ik (n) — ток к-й ветви от n-й э. д. с.
Порядок расчета
1. На основе исходной схемы составляют частные расчетные схемы (рис. 5.1, б, в), в каждой из которых действует только одна э. д. с. Все другие э. д. с. исключают и от каждого источника в схеме остается только его внутреннее сопротивление.
2. Любым подходящим методом определяют токи в частных схемах, которые чаще всего оказываются относительно простыми.
Для частных схем (рис. 5.1, б, в) выражения для токов, найденные путем свертывания, совпадают с (5.4), которые были записаны ранее из уравнений Кирхгофа. Например,
3. Алгебраическим сложением (наложением) частных токов определяют токи в исходной схеме. В рассматриваемом примере
При определении общих токов необходимо правильно учесть направления частных токов: в исходной схеме намечают условно-положительные направления токов в ветвях. Частный ток считают положительным, если он направлен одинаково с положительным током в той же ветви исходной схемы. Частный ток противоположного направления считают отрицательным.
При таком подходе общие токи в ветвях исходной схемы могут получиться положительными или отрицательными. В последнем случае надо изменить направление тока и считать его положительным в дальнейших расчетах.
Входные и взаимные проводимости и сопротивления
В равенствах (5.4) множители при э. д. с. имеют размерность проводимости. Обозначив их как проводимости, получим 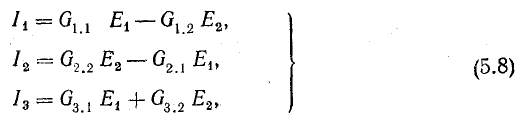
где 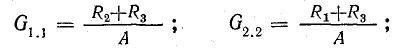
Коэффициенты с одинаковыми индексами называют входными проводимостями ветвей (G1.1; G2.2)- Коэффициенты с разными индексами называют взаимными проводимостими ветвей (G1.2; G2.1; G3.1; G3.2).
Если предположить, что э. д. с. Е2 = 0, из равенств системы (5.4) получим: 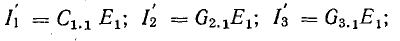
а при E1 = 0
Из этих выражений следует:
входная проводимость любой ветви равна отношению тока к э. д. с. этой ветви, если э. д. с. во всех остальных ветвях приняты равными нулю; входное сопротивление — величина, обратная входной проводимости:
Взаимная проводимость двух любых ветвей равна отношению тока в одной ветви к э. д. с. в другой ветви, если э. д. с. во всех остальных ветвях приняты равными нулю; взаимное сопротивление — величина, обратная взаимной проводимости: 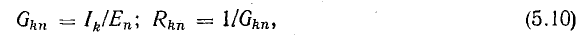
причем
Входные и взаимные проводимости и сопротивления можно определить расчетом, используя частные схемы, или найти путем измерений. После этого нетрудно найти токи в ветвях, составив равенства типа (5.8).
Коэффициенты передачи напряжения и тока
Режим электрической цепи в некоторых случаях характеризуется коэффициентами передачи напряжения и тока. Чаще всего они применяются к цепям, содержащим один источник э. д. с. (рис. 5.2, а) или один источник тока (рис. 5.2, б).
Коэффициент передачи напряжения равен отношению напряжения на зажимах приемника к напряжению источника э. д. с., действующего в цепи:
Коэффициент передачи тока равен отношению тока в приемнике к току источника тока, действующего в цепи: 
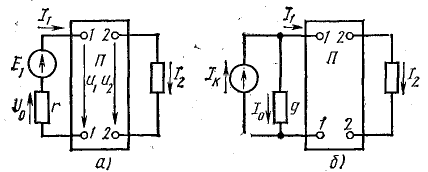
Рис. 5.2. К вопросу о коэффициентах передачи напряжений и токов
Задача 5.3.
Для цепи (рис. 5.3, а) известны: E1 = 120 В, Е2 = 100 В, R1 = 20 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 30 Ом.
Определить токи в цепи методом наложения.
Решение. Определим токи от действия каждой э. д. с. в отдельности по схемам, представленным на рис. 5.3, б, в. В схеме на рис. 5.3, б сопротивления R1 и R3 соединены параллельно. То же относится к паре сопротивлений R2 и R4.
Найдем эквивалентное сопротивление между точками 1-4:
Ток в неразветвленной части цепи
Сопротивления между точками 1-2 и 2-4 по данным задачи одинаковы (по 12 Ом). Поэтому
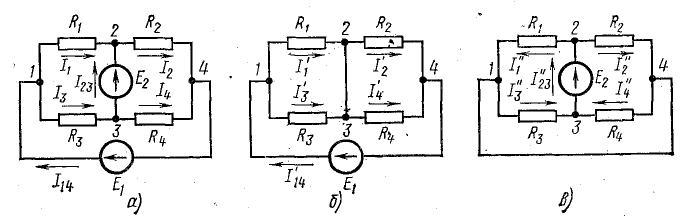
Рис. 5.3. К задаче 5.3
Токи в схеме 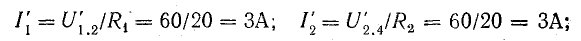
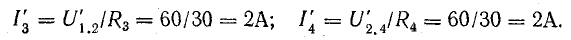
В схеме, изображенной на рис. 5.3, в, пары сопротивлений R1, R2 и R3, R4 соединены параллельно, а сопротивления, эквивалентные этим парам, — последовательно.
Найдем эквивалентные сопротивления схемы между точками 2-3: 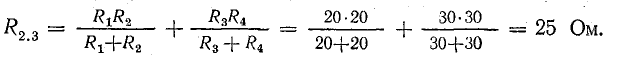
Ток в неразветвленной части цепи
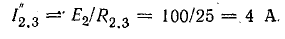
Напряжения на участках схемы между точками:
2-1
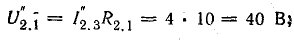
1-3
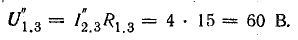
Токи в схеме 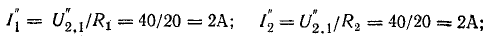
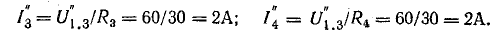
Токи в исходной схеме (рис. 5.3, а) найдем по принципу наложения, учитывая направления токов в частных схемах:
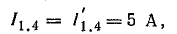
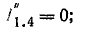
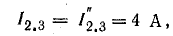
Метод эквивалентного генератора
В практических расчетах часто нет необходимости знать режимы работы всех элементов сложной цепи, но ставится задача исследовать режим работы одной определенной ветви.
Для определения тока, напряжения, мощности этой ветви можно воспользоваться одним из ранее описанных методов расчета.
При расчете сложной электрической цепи приходится выполнять значительную вычислительную работу даже в том случае, когда требуется определить ток в одной ветви. Объем этой работы в несколько раз увеличивается, если необходимо установить изменение тока, напряжения, мощности при изменении сопротивления данной ветви, так как вычисления нужно проводить несколько раз, задаваясь различными величинами сопротивления.
Решение такой задачи значительно упрощается при использовании метода эквивалентного генератора.
Обоснование метода
Исследуемая ветвь с сопротивлением Rab (рис. 5.5, а) присоединяется к остальной части схемы (внутри прямоугольника А) в двух точках a и b. Эту часть схемы можно рассматривать относительно исследуемой ветви как источник с некоторой эквивалентной э. д. с. Еэк и некоторым эквивалентным внутренним сопротивлением rэн (рис. 5.5, б). Такой условный источник энергии называется эквивалентным генератором или активным двухполюсником (А). Если в части схемы, относящейся к двухполюснику, нет источников энергии, то двухполюсник называется пассивным (П). 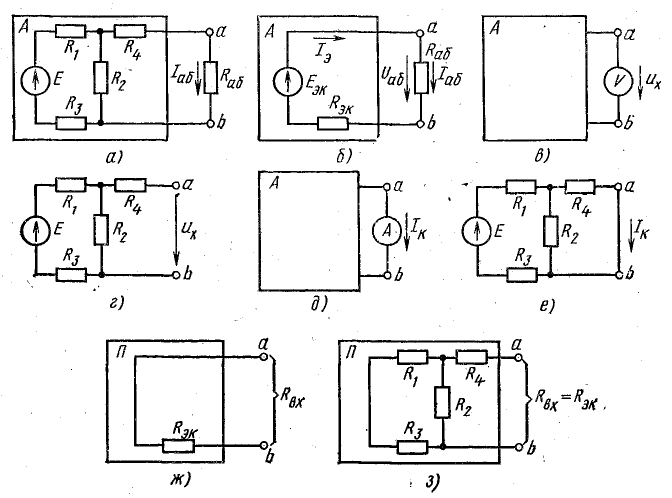
Рис. 5.5. К методу эквивалентного генератора
Ток в исследуемой ветви можно найти в эквивалентной схеме (рис. 5.5, б) по известной формуле (3.15):
Таким образом, решение задачи по определению тока Iab сводится к определению э. д. с. Еэк эквивалентного генератора и его внутреннего сопротивления rэк, которое называется также входным сопротивлением активного двухполюсника.
После определения Еэк и rэк дальнейшее исследование режима работы ветви ab при изменении сопротивления Rab не требует громоздких вычислений, так как э.д.с Еэк и внутреннее сопротивление rэк эквивалентного генератора не изменяются.
Ток в ветви ab определяют по формуле (5.12) для любого значения Rab.
Определение э.д.с. и внутреннего сопротивления эквивалентного генератора
Для определения этих величин рассмотрим два крайних режима эквивалентного генератора — режим холостого хода и режим короткого замыкания.
Отсоединим исследуемую ветвь Rab в точках a и b, тогда эквивалентный генератор будет находиться в режиме холостого хода.
Напряжение холостого хода Uх на его внешних зажимах a и b согласно схеме, представленной на рис. 5.5, б равно эквивалентной э. д. с.:
Напряжение холостого хода Uх можно измерить (рис. 5.5, в) или определить с помощью расчета (рис. 5.5, г). Для рассматриваемой цепи
Сопротивление R4 в расчет не вошло, так как при отключенном сопротивлении Rab ток в сопротивлении R4 тоже равен нулю.
Сопротивление rэк эквивалентного генератора можно определить, используя режим короткого замыкания.
В режиме короткого замыкания эквивалентного генератора (рис. 5.5, б) ток короткого замыкания Iк выражается отношением 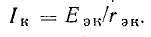
Отсюда
Для измерения тока Iк можно применить схему, изображенную на рис. 5.5, д, если короткое замыкание между точками a и b реальной цепи не вызовет опасного увеличения токов в ее элементах. При наличии такой опасности нужно измерить ток Iab нагрузки эквивалентного генератора и падение напряжения Uab в нагрузочном сопротивлении Rab (рис. 5.5, б), а внутреннее сопротивление
Ток Iк можно определить, применив один из известных методов расчета. Для рассматриваемого примера расчетная схема приведена на рис. 5.5, е.
Однако определение Iк может оказаться громоздким, поэтому в сложных схемах rэк определяется как входное сопротивление пассивного двухполюсника между точками a и b.
Для того чтобы получить расчетную схему для определения rэк, нужно все э. д. с. активного двухполюсника принять равными нулю, замкнув накоротко точки цепи, к которым присоединены источники этих э. д. с. Тогда активный двухполюсник превращается в пассивный.
Справедливость этого приема следует из схемы, представленной на рис. 5.5, б; при Еэк = 0 сопротивление rэк является входным сопротивлением этой схемы. Таким образом, входное сопротивление пассивного двухполюсника Rвх со стороны зажимов a и b (рис. 5.5, ж) определяет внутреннее сопротивление rэк эквивалентного генератора.
Равенство Еэк = 0 соответствует тому, что все э. д. с. активного двухполюсника равны нулю, поэтому расчетная схема для определения rэк имеет вид, как на рис. 5.5, з.
Для этой схемы
Задача 5.5.
Построить графики зависимости тока и мощности в ветви 2-4 (см. рис. 5.3, а) от сопротивления в этой ветви по данным условия задачи 5.1.
Решение. Для решения задачи применим метод эквивалентного генератора.
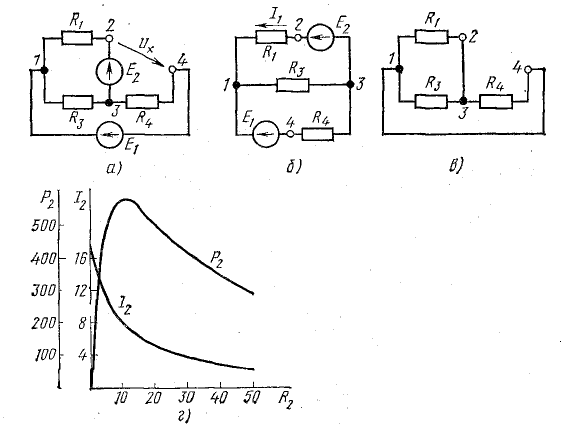
Отключим ветвь 2-4 для определения напряжения холостого хода (рис. 5.6, а). После отключения ветви 2-4 получилась схема с двумя узловыми точками 1 и 3, изображенная в несколько ином виде на рис. 5.6, 6.
Рис. 5.6. К задаче 5.5
Для расчета этой схемы целесообразно применить метод узлового напряжения:
Для определения разности потенциалов между точками 2 и 4 найдем ток 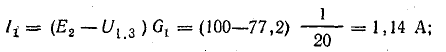
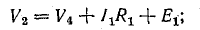
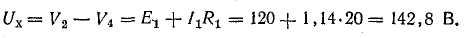
Для определения внутреннего сопротивления эквивалентного генератора полагаем равными нулю действительные э. д. с. исходной схемы.
Получим схему, представленную на рис. 5.6, в, из которой видно, что по отношению к точкам 2 и 4 все три сопротивления пассивного двухполюсника соединены параллельно:
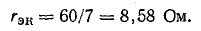
Ток в исследуемой ветви определим по формуле (5.12), задаваясь различными величинами сопротивления.
Для сопротивления R2 = 20 Ом получим:
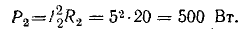
Для других значений сопротивления R2 результаты подсчетов сведены в табл. 5.1.
| R2, Ом | 0 | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 50 | ∞ |
| I2, А P2, Вт | 16,6 0 | 13,5 364 | 11,35 515 | 9,8 575 | 8,6 592 | 7,7 590 | 5 500 | 3,7 410 | 2,42 290 | 0 0 |
Графики I2(R2) и P2(R2) показаны в прямоугольной системе координат из рис. 5.5, г.
Метод контурных токов
Число узловых и контурных уравнений для сложной схемы оказывается большим, а решение системы m уравнений — громоздким. Число уравнений можно уменьшить до m — n + 1 и тем существенно упростить расчет, если ввести понятие контурных токов и применить их для решения задачи.
Контурные токи и э.д.с.
Рассмотрим в качестве примера уже известную схему рис. 3.16 и выделенные в ней ранее четыре независимых контура, для которых записаны уравнения (5.2). Заметим, что, применяя метод контурных токов, источники энергии удобнее представлять в схемах их э, д. с. и внутренними сопротивлениями. В данной схеме внутренние сопротивления источников энергии равны нулю (или отнесены к приемникам).
Контурный ток — это некоторая расчетная величина, которая одинакова для всех ветвей данного контура. Контурные токи на схеме обозначены II ; III ; IIII ; IIV .
Нетрудно заметить, что контурный ток равен действительному току ветви, которая принадлежит только данному контуру: 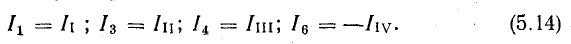
Некоторые ветви схемы относятся к двум смежным контурам (ветви 1-3; 3-6; 4-6).
Действительный ток в такой ветви определяется наложением контурных токов, т. е. равен алгебраической сумме контурных токов тех контуров, в которые эта ветвь входит:
В уравнениях (5.2) заменим токи ветвей их выражениями через контурные токи (5.14), (5.14 а): 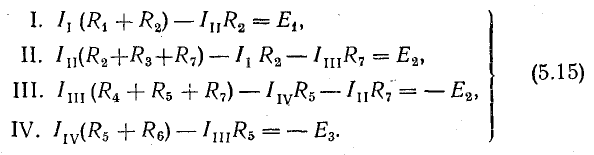
В правую часть этих уравнений входят э. д. с. источников, встречающихся при обходе данного контура.
Алгебраическая сумма э. д. с. данного контура называется контурной э. д. с.
В данном примере в каждом контуре по одной э. д. с., поэтому контурные э. д. с.: ЕI = Е1; ЕII = Е2; ЕIII = — Е2; ЕIV = — Е3.
Если в данный контур не входят источники э. д. с., то контурная э. д. с. его равна нулю.
Собственные и общие сопротивления контуров
В левую часть уравнений (5.15) входят падения напряжения, обусловленные контурными токами.
Сумма сопротивлений всех ветвей, входящих в данный контур, называется собственным сопротивлением контура.
Для схемы рис. 3.16 собственные сопротивления контуров:
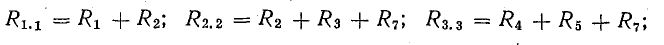
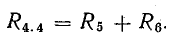
Сопротивления ветвей, входящих в два смежных контура, называются общими сопротивлениями контуров. Такими сопротивлениями в схеме рис. 3.16 являются R1.2 = R2; R2.3 = R7; R3.4 = R5.
При определении собственных и общих сопротивлений внутренние сопротивления источников э. д. с. учитываются как и сопротивления приемников энергии.
Метод контурных токов
С учетом новых понятий и обозначений перепишем уравнения (5.15):
Решая эту систему уравнений любым способом, известным из алгебры, определяют контурные токи, а по формулам (5.14) и (5.14а) находят токи в ветвях.
В данном примере вместо семи узловых и контурных уравнений для расчета достаточно четырех уравнений с четырьмя контурными токами.
Из всего сказанного следует порядок составления уравнений с контурными токами.
- В заданной схеме выбирают направления токов в ветвях (произвольно).
- Намечают независимые контуры и выбирают направление контурных токов, например по часовой стрелке.
- Определяют контурные э. д. с., собственные и общие сопротивления контуров, обходя контуры в направлении контурных токов.
- Записывают систему уравнений типа (5.16); в левой части их слагаемые с собственными сопротивлениями контуров берут со знаком плюс, а слагаемые с общими сопротивлениями — со знаком минус.
Метод узловых напряжения
Законы Кирхгофа являются основой для расчета электрических цепей методом узловых напряжений, который позволяет сократить число уравнений в системе до n — 1, где n — число узлов.
Узловые напряжения и токи
Для данных рассуждений примером может служить схема рис. 3.16. Однако, применяя метод узловых напряжений, удобнее источники э. д. с. заменить эквивалентными источниками токов на основе выводов, что и показано на рис. 5.7.
Рис. 5.7. К методу узловых напряжений
Источники энергии на рисунке представлены токами короткого замыкания Iк1 = E1G1; Iк2 = E2G7; Iк3 = E3G6, а внутренние проводимости их приняты равными нулю или отнесены к приемникам.
Один из узлов схемы принимается базисным, и его потенциал считается равным нулю (узел 6, V6 = 0).
Узловым напряжением называется разность потенциалов между данным узлом и базисным. В рассматриваемой схеме узловые напряжения 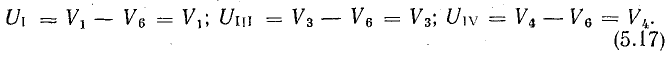
Выразим напряжения ветвей через узловые напряжения. Нетрудно заметить, что узловое напряжение численно равно напряжению ветви, которая присоединена к базисному узлу: 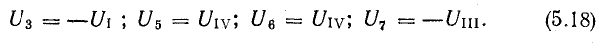
Напряжение ветви, не присоединенной к базисному узлу, равно разности узловых напряжений тех узлов, между которыми находится эта ветвь: 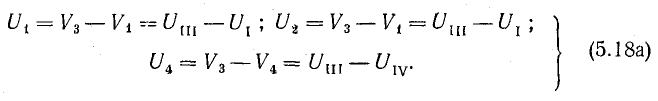
По первому закону Кирхгофа составим систему уравнений для трех независимых узлов (кроме базисного) рассматриваемой схемы: 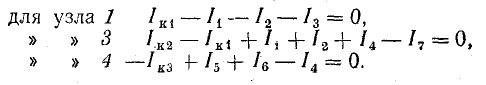
Эти уравнения перепишем так, чтобы в правой части их были только внутренние токи источников тока, из которых складываются узловые токи: 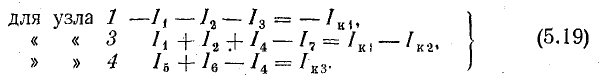
Узловым током называется алгебраическая сумма внутренних токов источников тока всех ветвей, присоединенных к данному узлу.
В этой сумме токи источников тока, направленные к узлу, считаются положительными, а от узла — отрицательными: 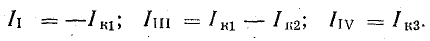
Если к некоторому узлу не присоединены ветви с источниками токов, то его узловой ток равен нулю.
Узловые и общие проводимости
Выразим токи ветвей через напряжения и проводимости этих ветвей: 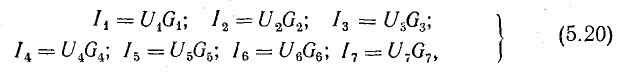
а учитывая (5.18), систему уравнений (5.19) представим в следующем виде: 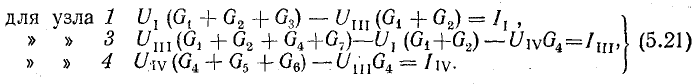
Узловой проводимостью называется сумма проводимостей всех ветвей, присоединенных к данному узлу.
В системе уравнений (5.21) узловые проводимости выражаются так: 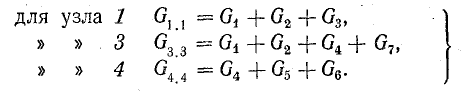
Общей проводимостью называется сумма проводимостей всех ветвей, соединяющих данные два узла.
В системе уравнений (5.21) общие проводимости G13 = G1 + G2; G3.4 = G4.
С учетом новых обозначений уравнения (5.21) перепишем так:
Метод узловых напряжений
Решая систему уравнений (5.22) любым способом, известным из алгебры, определяют узловые напряжения, затем по (5.18), (5.18, а) находят напряжения ветвей, а по формулам (5.20) — токи ветвей.
В данном примере вместо семи узловых и контурных уравнений для расчета достаточно трех уравнений с тремя узловыми напряжениями.
Из всего сказанного следует порядок составления уравнений с узловыми напряжениями.
- В заданной схеме выбирают направления токов в ветвях (произвольно). Если по условию источники энергии заданы как источники э. д. с. (напряжения), переходят к эквивалентным схемам источников тока.
- Намечают базисный узел и все независимые узлы и выбирают положительные направления узловых напряжений — от независимых узлов к базисному.
- Определяют узловые токи, узловые и общие проводимости; при этом токи источников тока, направленные к узлам, принимают положительными.
- Записывают систему уравнений типа (5.22); в левой части уравнений слагаемые с узловыми проводимостями берут со знаком плюс, а слагаемые с общими проводимостями — со знаком минус.
Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Методы расчета сложных электрических цепей
Основные теоретические сведения:
Для расчета токов и напряжений в сложных электрических цепях разработаны разработаны методы, базирующиеся на основных законах токопрохождения, принципах (теоремах) теории цепей:
- Метод уравнений Кирхгофа (МУК).
- Метол контурных токов (MKT).
- Метол узловых напряжений (МУН).
- Метод сигнальных графов.
- Метод наложения (МН),
- Метод эквивалентного генератора (МЭГ) и другие методы.
Четыре первых метода являются универсальными, позволяющими в принципе рассчитать цепь любой сложности. С помощью других методой обычно решают частные (локальные) задачи. В ряде случаев решение задачи удается упростить, если предварительно произвести эквивалентные преобразования схемы цени.
Для решения конкретной задачи обычно выбирают метод, позволяющий описать цепь минимальным числом уравнений.
Анализ структуры электрической цепи
Анализ структуры цепи производят с целью определения числа ветвей с неизвестными токами и чисел независимых узлов и контуров.
р — число ветвей с неизвестными токами, включающими все ветви цепи, за исключением ветвей с источниками токов; q — число узлов в цепи; НУ — число независимых узлов в цепи; НК — число независимых контуров в цепи.
Анализируя цепь, легко показать, что
Если электрическая цепь имеет достаточно простую структуру, то числа p и q определяются легко. Для анализа сложных разветвленных цепей строят топологический граф и дерево цепи. При этом ветвь и узел цепи отождествляются соответственно с ребром и узлом графа.
Внутреннее сопротивление идеального источника напряжения равно нулю. Поэтому ветвь, содержащая только этот источник, закорачивается и не образует ребра на графе цепи, вырождаясь в узел.
Внутреннее сопротивление идеального источника тока бесконечно велико, поэтому при построении графа цепи ветвь с таким источником разрывается.
Расчет электрических цепей методом уравнений Кирхгофа
Суть метода уравнений Кирхгофа состоит в том, что неизвестные токи и напряжения в цепи рассчитываются непосредственно из системы уравнений, составленных по законам Кирхгофа. По первому закону Кирхгофа составляют уравнения для независимых узлов, а по второму — для независимых контуров. При этом число уравнений в системе равно числу неизвестных токов в ветвях: 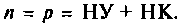
Порядок расчета:
- составляют комплексную схему замещения цепи;
- производят структурный анализ пени;
- выбирают условно положительные направления токов в ветвях, напряжений на элементах и направления обхода контуров;
- составляют для НУ уравнения по первому закону Кирхгофа и для НК уравнения по второму закону Кирхгофа относительно неизвестных токов в ветвях;
- по решению системы уравнений рассчитывают неизвестные токи в ветвях и неизвестные напряжении на элементах цепи.
Расчет электрических цепей методом контурных токов
Суть метода контурных токов состоит в том, что вводятся дополнительные формальные неизвестные — контурные токи, которые определяются из системы контурных уравнений, составленных по второму закону Кирхгофа. Далее, по известным контурным токам рассчитывают искомые токи в ветвях, а затем искомые напряжения на элементах.
Контурным током 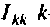
Направления контурных токов в цепи выбираются произвольно. Для составления контурных уравнений в канонической форме вводятся три вспомогательных понятия: контурная ЭДС, собственное сопротивление независимого контура, общее сопротивление двух независимых контуров.
Контурной ЭДС 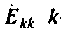
Собственным сопротивлением 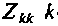
Общим сопротивлением 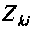
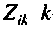
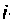
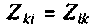
Как правило, направления всех контурных токов выбирают одинаковыми, например по часовой стрелке. Можно показать, что в этом случае все общие сопротивления должны иметь знак, противоположный знаку сопротивления общей ветви данных контуров.
С учетом введенных величин запишем систему линейных контурных уравнений в матричной форме, удобной для расчета с помощью определителей: 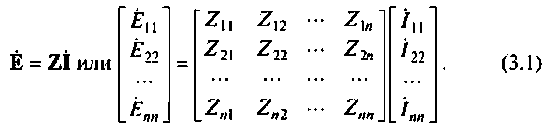
Если система (3.1) определенная, то контурные токи можно найти по формулам Крамера: 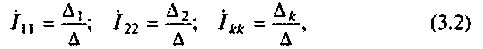
где 
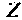
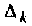
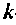
По известным контурным токам легко определить искомые токи и ветвях. Ток в ветви, принадлежащей только одному 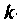
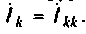
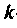
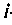
В систему (3.1) контурных уравнений входят только ЭДС источников напряжения. Поэтому при расчете все источники тока в цепи необходимо заменить эквивалентными источниками напряжения (см. табл. 2.1).
Порядок расчета:
- составляют комплексную схему замещения цепи;
- производят структурный анализ цепи;
- выбирают условно положительные направления токов в ветвях и контурных токов;
- составляют по второму закону Кирхгофа систему уравнений вида (3.1) относительно неизвестных контурных токов;
- рассчитывают по известным параметрам цепи собственные и общие сопротивления независимых контуров, их контурные ЭДС;
- рассчитывают неизвестные контурные токи, а затем неизвестные токи в ветвях и напряжения на элементаx цели.
Примечание. Если при расчете производили эквивалентную замену источников тока в ветвях цепи источниками напряжения, то для расчета токов в этих ветвях необходимо перейти к исходной схеме.
Расчет электрических цепей методом узловых напряжений
Суть метода узловых напряжении состоит в том, что вводятся дополнительные неизвестные — узловые напряжения, которые находятся из системы узловых уравнений, составленных по первому закону Кирхгофа. Далее по известным узловым напряжениям рассчитывают искомые токи в ветвях, а затем — искомые напряжения на элементах.
Узловым напряжением 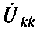
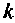
Направление узловых напряжений выбирают произвольно. Наиболее часто полагают, что все узловые напряжения направлены к базисному узлу. Для составления узловых уравнений в канонической форме вводятся три вспомогательных понятия: узловой ток; собственная проводимость независимого узла; общая проводимость двух независимых узлов.
Узловым током 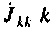
Собственной проводимостью 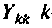
Общей проводимостью 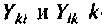
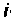
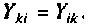
Если направления всех узловых напряжений выбраны одинаковыми, например, к базисному узлу, то общие проводимости должны иметь знак, противоположный знаку проводимостей общих ветвей данных узлов.
С учетом введенных величин запишем систему линейных узловых уравнений в матричной форме
:
Если система (3.3) определенная, то узловые напряжения можно рассчитать но формуле Крамера:
где 
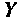
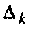
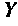
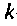
По известным узловым напряжениям легко найти искомые токи. Если в ветви нет источника, то ток рассчитывают но закону Ома. Если в ветви есть источник напряжения, то для расчета тока удобно воспользоваться вторым законом Кирхгофа.
Порядок расчета:
- составляют комплексную схему замещения цепи;
- производят структурный анализ цепи;
- выбирают условно-положительные направления токов в ветвях и узловых напряжений;
- составляют по первому закону Кирхгофа систему уравнений вида (3.3) относительно неизвестных узловых напряжений:
- рассчитывают по известным параметрам цепи собственные и общие проводимости независимых узлов и узловые токи;
- рассчитывают неизвестные узловые напряжения, а затем неизвестные токи в ветвях и напряжения на элементах.
Примечание. Если при расчете производили эквивалентную замену источников напряжения источниками токи, то для расчета токов в преобразованных ветвях необходимо перейти к исходной схеме.
Расчет электрических цепей методом наложения
Сущность метода наложения состоит в том, что в соответствии с принципом наложения неизвестные токи в ветвях определяют как алгебраическую сумму частичных токов, обусловленных действием каждого источника отдельно.
Для расчета частичных токов исходную цепь с 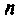
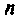
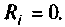
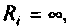
Для расчета токов в частных схемах можно использовать любой метод, а для упрощения расчетов предварительно производят эквивалентные преобразования в цепи. В достаточно простых цепях при расчете удобно использовать известные приемы расчета делителей тока и напряжения.
Порядок расчета:
- составляют комплексную схему замещения цепи;
- составляют частные схемы, содержащие по одному источнику;
- рассчитывают частичные токи в ветвях;
- определяют искомые токи как алгебраические суммы частичных токов в соответствующих ветвях.
Расчет цепей методом эквивалентного генератора
Суть метода эквивалентного генератора состоит в том, что всю электрическую цепь, кроме одной ветви с неизвестным током, заменяют эквивалентным генератором с параметрами 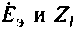
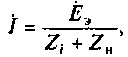
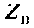
Теорема об эквивалентном генераторе утверждает, что ЭДС эквивалентного генератора равна напряжению холостого хода активного двухполюсника, а его внутреннее сопротивление равно входному сопротивлению двухполюсники:
Напряжение можно определить экспериментально или рассчитать по схеме цепи. Для расчета напряжения необходимо по второму закону Кирхгофа составить уравнение для входного контура, который содержит зажимы эквивалентного генератора (расчетную ветвь).
Для расчета входного сопротивления эквивалентного генератора необходимо составить схему пассивною двухполюсника, т.е. исключить в исходной цепи все источники, заменив их соответствующими внутренними сопротивлениями. Далее, используя известные приемы эквивалентного преобразования схемы цепи, находят входное сопротивление.
Порядок расчета:
- составляют комплексную схему замещения цепи;
- исключают из схемы ветвь с искомым током (нагрузку), обозначая зажимы генератора с напряжением холостого хода;
- составляют для входного контура уравнение но второму закону Кирхгофа и рассчитывают
- составляют схему пассивного двухполюсника, считая входом зажимы эквивалентного генератора, и рассчитывают его входное сопротивление;
- рассчитывают искомый ток.
Примеры решения задач
Пример 3.2.1.
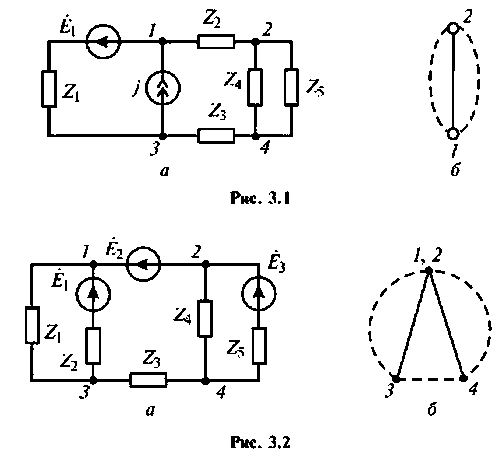
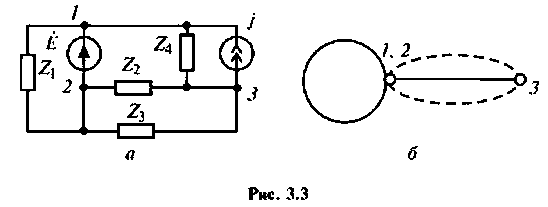
Произвести структурный анализ цепей, схемы которых приведены на рис. 3.1, а; 3,2, а; 3,3, а.
При поверхностном анализе структуры цепи рис. 3.1, а может сложиться мнение, что цепь имеет три независимых контура и три независимых узла. Однако из-за наличия в цепи идеального источника тока узлы 1 и 3 являются устранимыми. Это становится очевидным, если построить граф цепи (рис, 3,1, б), При построении графа ветвь с источником тока размыкается, поэтому узлы 1, 3 и 4 образуют узел.
Следует заметить, что в ветвях с сопротивлениями 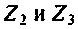
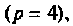
На графе для цепи, показанной на рис.3.2,а, из-за наличия идеального источника ЭДС 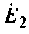
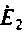
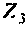
Построение дерева и графа для цепи (рис. 3.3, а) показывает, что в данном случае имеется один независимый узел и два независимых контура. Включение в цепь идеального источника 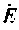
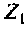
Поэтому анализ показывает, что в данной цепи (рис.3.3, а)
Пример 3.2.2.
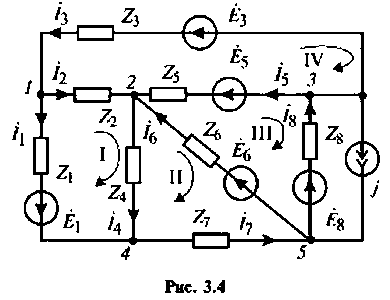
Составить по методу уравнений Кирхгофа систему уравнений для расчета токов в ветвях цепи (рис. 3.4).
Решение
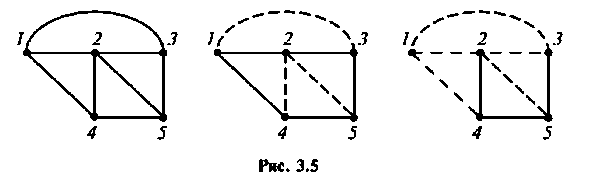
1. Произведем структурный анализ цепи. На рис. 3.5 показаны граф и деревья цепи (хорды графа обозначены пунктиром). Анализ показывает, что число неизвестных токов 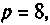
2. Зададимся условно-положительными направлениями токов в ветвях и напряжений на элементах (см. рис. 3.4), а также направлением обхода контуров
3. Считая узлы 1, 2, 3 и 4 независимыми, составим для них уравнения по первому закону Кирхгофа:
Токи, направленные к узлу, учитываются и уравнениях со знаком (+), направленные от узла — со знаком (-).
4. Выбрав независимые контуры I—IV (см, рис. 3.4), составим для них уравнения по второму закону Кирхгофа:
Примечание. Падения напряжений на элементах контуров выразим через искомые токи в ветвях.
Совместное решение полуденных восьми уравнений позволяет рассчитать все неизвестные токи в ветвях, а затем, если необходимо напряжения на элементах цепи.
Из приведенного примера видно, что достоинство метода уравнений Кирхгофа заключается в его простоте (с точки зрения составления уравнений). Недостаток этого метода — сложность решения системы уравнений из-за большого числа уравнений и их разнородности.
Пример 3.2.3.
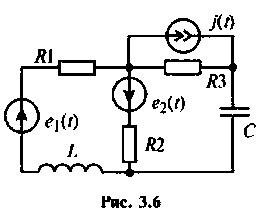
Рассчитать токи в ветвях цепи (рис. 3.6) методом контурных токов.
Решение
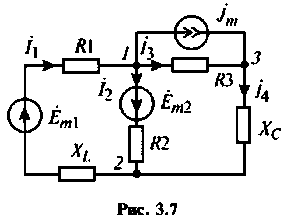
1. Составляем комплексную схему замещений цепи (рис. 3.7).
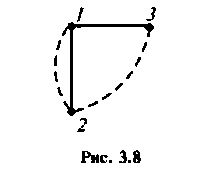
2. Произведем структурный анализ цепи с помощью топологического графа (рис.З.8). Анализ цепи показывает, что она содержит пять ветвей, а число ветвей с неизвестными токами р = 4. Цепь имеет 1ри узла, причем узел 3 является устранимым. Поэтому независимых узлов в схеме q = 2. Очевидно, что число независимых контуров равно двум (число хорд на графе): НК = 4- 3 + 1 = 2.
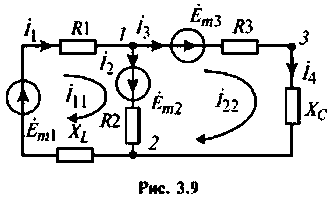
3. Реальный источник тока заменяем эквивалентным источником напряжения и выбираем направления контурных токов (рис. 3.9).
4. Составляем каноническую систему контурных уравнений для независимых контуров в матричной форме
5. Рассчитаем собственные и общие сопротивления и контурные ЭДС:
6. Рассчитаем контурные токи по формулам Крамера:
Рассчитаем определитель системы
Рассчитаем частные определители системы:
Тогда контурные токи будут соответственно равны:
7. Рассчитаем токи в ветвях через контурные токи:
8. Проверим достоверность произведенного расчета по балансу мощности. Мощности, отдаваемые источниками в цепь:
Таким образом, общая мощность источников равна
Активная и реактивная мощности в пассивных элементах цепи равны соответственно:
Как видно из приведенных расчетов, отдаваемая и потребляемая мощности в электрической цепи совпадают.
Пример 3.2.4.
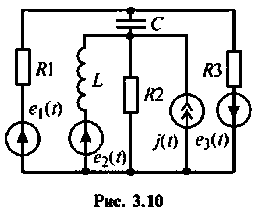
Рассчитать токи в ветвях цепи (рис.3.10) методом узловых напряжений.
Решение
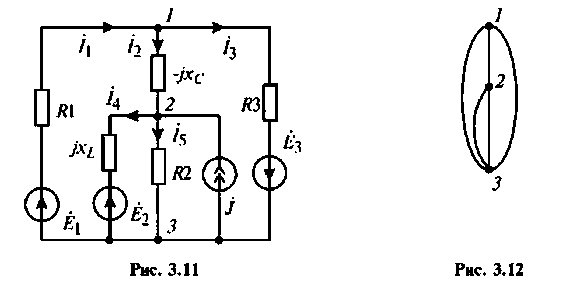
1. Составим комплексную схему замещения (рис. 3.11) и определим комплексные источники ЭДС и тока:
2. Произведем структурный анализ цепи с помощью топологического графа (рис. 3.12).
Анализ цепи показывает, что она содержит 6 ветвей, а ветвей с неизвестными токами р= 5. Число независимых узлов составляет
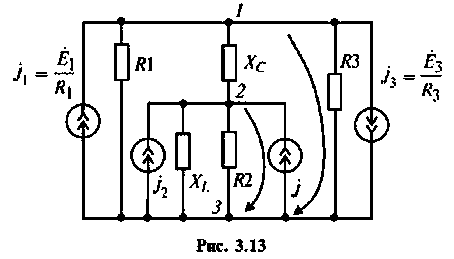
3. Ветви с реальными источниками напряжения заменим эквивалентными источниками тока (рис. 3.13) и выберем направления узловых напряжений.
4.Составим каноническую систему уравнений для независимых узлов и рассчитаем собственные и общие проводимости и узловые токи.
5. Рассчитаем узловые напряжения по формулам Крамера:
Составим и рассчитаем определители системы:
Тогда узловые напряжения равны:
6. Рассчитаем токи в ветвях по законам Ома и Кирхгофа.
Токи в ветвях по найденным узловым напряжениям находятся из уравнений, составляемых по второму закону Кирхгофа для исходной непреобразованной схемы. При этом контур замыкается через ветвь с искомым током и найденными узловыми напряжениями. Так, если путем решения системы уравнений найдены узловые напряжения 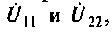
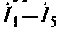
Пример 3.2.5.
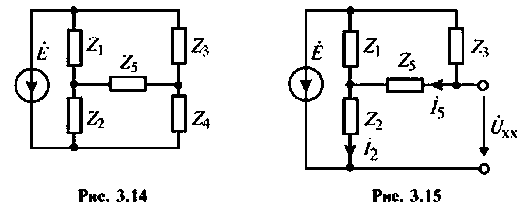
Определить ток в сопротивлении 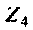
Дано:
Решение
1. Составим схему для определения напряжения холостого хода (рис.3.15) и рассчитаем 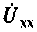
Для определения 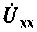
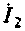
2.Составим схему для определения внутреннего сопротивления эквивалентного генератора (рис. 3.16) и рассчитаем его.
3. Рассчитаем ток
Пример 3.2.6.
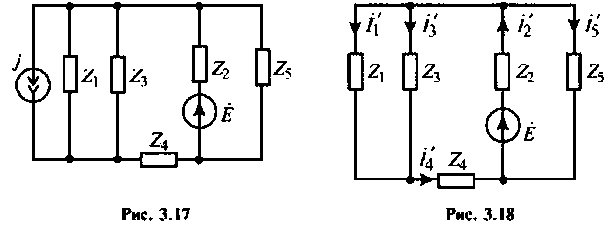
Рассчитать токи в ветвях цепи (рис. 3.17) методом наложения.
Дано:
Решение
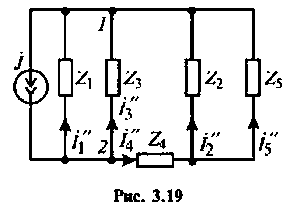
1.Составляем частную схему с источником ЭДС (рис. 3.18) и выбираем произвольно направление токов в ветвях цепи.
2. Рассчитаем частичные токи в ветвях:
3. Составляем частную схему с источником тока (рис. 3.19).
4. Рассчитаем частные токи в ветвях. Для расчета определим напряжение между узлами 1 и 2 схемы:
5. Рассчитаем комплексные токи в ветвях исходной схемы, как алгебраическую сумму частичных токов:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод узловых напряжений
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Метод контурных токовСкачать

Лекция 117. Правила КирхгофаСкачать

МКТ │Цепь с источниками тока │Расчет цепи методом контурных токовСкачать

Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Электротехника (ТОЭ). Лекция 4. Метод контурных токов | Решение задачСкачать

Правила Кирхгофа - определение токов. ЭлектротехникаСкачать
Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Лекция 020-3. Метод контурных токовСкачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

1 4 3 Метод узловых напряжениеСкачать

ОЛИМПИАДНАЯ ЗАДАЧА ПО ТОЭ #3 | МЕТОД КОНТУРНЫХ ТОКОВСкачать