- 1. Стоит ли тратить время на чтение этой статьи?
- 2. Аналитика себестоимости в ут11
- 3. Центры затрат в 1с 8.2 ут 11
- 4. РАУЗ – Средняя за месяц
- 5. Граф затрат
- 6. РАУЗ – ФИФО (взвешенная оценка)
- 7. РАУЗ – ФИФО (скользящая оценка)
- 8. Отрицательные остаткив 1с 8.2 ут11
- Заключение
- Чтобы еще почитать?
- Решение системы линейных уравнений
- Ваш браузер устарел, пожалуйста обновите ваш браузер пройдя по ссылке www.microsoft.com/download
- Решение СЛАУ на примере распределения транспортных расходов.
- Решение.
- 1. Составляем таблицу движений
- 2. Составление таблицы СЛАУ
- 📺 Видео
Видео:#14. Как мы в платформе реализовали расчет СЛАУ, и что там под капотом. Старичков Никита. 26.03.2020Скачать

1. Стоит ли тратить время на чтение этой статьи?
Эта статья является прямым следствием курса 1С:Управление торговлей – Быстрый старт: Затраты, Себестоимость, Финансы. Причиной, побудившей меня бегом бежать на этот курс, стало заявление его авторов Евгения Гилева и Фарита Насипова рассказать о том, как работает РАУЗ.
Непонимание того, какую систему уравнений и, каким образом формирует конфигурация для расчета себестоимости товаров, лично меня останавливало от изучения таких программ, как 1С:Комплексная автоматизация 8 и 1С:Управление производственным предприятием 8.
Получив первоначальные знания по этому вопросу, я решил привести их в порядок. В результате появилась эта статья. Однако, завершив статью, я понял, что обычному пользователю нет особой необходимости разбираться в том, как устроен РАУЗ. Как формируется система линейных уравнений.
Судите сами. У пилота авиалайнера на приборной доске огромное количество приборов. У оператора атомной электростанции блочный щит управления занимает несколько десятков квадратных метров. Представляете сколько на нем приборов! Конечно, пилот или оператор в общих чертах знают принципы их работы. Но в деталях обычно не разбираются. Это совершенно другая область знаний. Для успешного управления авиалайнером или АЭС им необходимо быть уверенными, что все эти приборы работают исправно.
Тоже самое и с технологией РАУЗ. Для пользователя важно правильно настроить программу и корректно отражать хозяйственные операции. А с расчетом себестоимости программа справится самостоятельно. Если же вы, как и я испытываете дискомфорт от непонимания алгоритма расчета себестоимости, тогда эта статья может оказаться вам полезной. В противном случае не теряйте время, займитесь чем-то более приятным.
И еще, чтобы не ввести вас в заблуждение, будто РАУЗ это просто расчет себестоимости путем решения системы линейных уравнений (СЛУ), познакомьтесь сначала со статьей РАУЗ на пальцах или пять аспектов технологии РАУЗ в программе 1С:Управление торговлей редакция 11. Рекомендую также и статью Принципы расчета себестоимости товаров в 1С:Управление торговлей редакция 11.
Вероятно, главным аспектом РАУЗ является оценка себестоимости товаров путем автоматического формирования СЛУ и ее последующего решения. Поэтому их частенько отождествляют. Данная статья на простых примерах показывает, как система формирует СЛУ.
Для справки. Несмотря на то, что программа 1С:Управление торговлей редакция 11 является управленческой, тем не менее, разработчики в основу расчета себестоимости положили требования ПБУ 5/01 и Приказ Минфина от 28.12.2001 № 119. См. 75-78.
Статья посвящена описанию алгоритма формирования СЛУ в программе 1С:Управление торговлей редакция 11.1. Для краткости будем употреблять аббревиатуры ут11 или ут 11. Там, где надо будет подчеркнуть отличия, будем полностью указывать редакцию продукта: ред. 11.1 или ред. 11.0.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

2. Аналитика себестоимости в ут11
Себестоимость товаров в программе ут11 рассчитывается в разрезе соответствующих аналитик. В ред. 11.1 и ред. 11.0 такими аналитиками являются измерения регистра накопления «Себестоимость товаров»:
- АналитикаУчетаНоменклатуры.
- Раздел учета,
- Вид запасов.
- Организация,
Измерение «АналитикаУчетаНоменклатуры» ссылается на одноименный справочник «Ключи аналитики учета номенклатуры». По терминологии разработчиков ключ аналитики – это объект, который объединяет в себе несколько аналитических разрезов учета. В 1С ут11 он включает в себе еще три дополнительных аналитики расчета себестоимости товаров:
Итого получается 6 аналитик, в разрезе которых рассчитывается себестоимость.
- Организация.
- Склад.
- Вид запасов.
- Номенклатура.
- Характеристика.
- Раздел учета.
В отличие от ред. 10.3 в конфигурации ут11 эти аналитики обладают некоторыми особенностями. Опишем их вкратце.
Организация. Справочник «Организации».
Учет себестоимости ведется в разрезе организаций, но не ведется в целом по предприятию. Это может показаться удивительным, ведь конфигурация ут 11 управленческая. Но это так. В целом по предприятию учет себестоимости не ведется.
Данные по любой организации, за исключением предопределенной организации «Управленческая организация», могут быть выгружены в программу 1С:Бухгалтерия 8. Это означает, что, если на предприятии есть операции, которые не должны отражаться в регламентированном учете, то их следует отражать в организации «Управленческая организация».
Такая организация создается системой автоматически, если в разделе «Администрирование Организации и финансы» установить флаг «Раздельные операции закупок и продаж для упр. и регл. учета».
Склад. Справочник «Склады (складские территории)».
В 1с 8.2 ут 11 под складом в общем случае понимается некоторая складская территория. Количество складских территорий не ограничено.
Складские территории можно разделить на складские помещения. Учет по складским помещениям возможен только на оптовых складах, для которых предусмотрена возможность ордерной схемы документооборота по операциям поступления, выбытия и отражения излишков и недостач.
В свою очередь на складских территориях и в складских помещениях можно предусмотреть адресное хранение товаров. Для этого необходимо включить возможность создания складских ячеек.
С точки зрения расчета себестоимости важно знать, что она рассчитывается в разрезе складских территорий. Другими словами товар, хранящийся в разных помещениях и в разных ячейках, принадлежащих одной и той же складской территории, обладает одним и тем же значением себестоимости.
Вид запасов. Справочник «Виды запасов».
Виды запасов хранятся в одноименном справочнике «Виды запасов». Нужные элементы создаются автоматически при оформлении поставки товаров.
В ред. 11.1 появилась возможность указания видов запасов и номеров ГТД вручную из документов выбытия товаров (реализация, перемещение, сборка). Для этого в табличной части документа надо нажать на кнопку «Открыть виды запасов».
Каждый вид запаса определяется набором следующих реквизитов.
- Организация. Элемент справочника «Организации».
- Тип запасов. Возможные типы запасов описаны в перечисление «Типы запасов», которое может принимать одно из значений: Товар, Материал, Комиссионный товар, и Услуга. В ред. 11.0 была еще и Тара. В ут11.1 почему-то ее убрали.
- Налогообложение. Возможные типы налогообложения описаны в перечисление «Типы налогообложения НДС»: Продажа облагается НДС, Продажа не облагается НДС, Продажа на экспорт (ставка 0%) и Продажа облагается ЕНВД.
- Комитент. Элемент справочника «Партнеры».
- Соглашение с комитентом. Элемент справочника «Соглашение с поставщиками».
- Валюта взаиморасчетов. Элемент справочника «Валюты»
- Реализация запасов другой организации. В конфигурации 1с 8.2 ут 11 предусмотрена возможность продажи товаров между организациями своей компании. Данный реквизит относится к типу Булево и может принимать значение Ложь (по умолчанию) или значение Истина. «Что же такое “Интеркампани”?» http://курсы-по-1с.рф/post-2013-01/trade11-faststart-article010/ великолепно описал Голиков Александр Борисович. Он оказался победителем конкурса финалистов «1С:Управление торговлей – Быстрый старт: Затраты, Себестоимость, Финансы».
- Вид запасов организации — владельца товара. Определяется совокупностью значений реквизитов справочника «Виды запасов». Видимо, имеется в виду следующее. В рамках схемы интеркомпани одна организация нашей компании может выступать комиссионером, а другая комитентом. В этом случае для комиссионера в этом реквизите указывается вид запаса комитента.
- Способ передачи товаров. Возможные способы передачи товаров описаны в перечисление «Способы передачи товаров»: Продажа, Продажа и возврат, Передача на комиссию, Передача на комиссию и возврат, Не передается или Не требуется.
- Поставщик. Элемент справочника «Партнеры».
- Предназначение. Возможные типы предназначения товаров описаны в перечисление «Типы предназначения видов запасов»: Предназначен для сделки, Предназначен для подразделения, Предназначен для менеджера, Предназначен для заказа (Это новое значение, в ут11.0 оно отсутствует) или Предназначение не ограничено.
- Подразделение. Элемент справочника «Структура предприятия». Так как конфигурация управленческая, то у в организациях нет подразделений. Структура подразделений описывается в целом для предприятия.
- Менеджер. Элемент справочника «Пользователи».
- Сделка. Элемент справочника «Сделки с клиентами».
- Деятельность облагается ЕНВД. Не используется.
- Группа финансового учета. Элемент справочника «Группы финансового учета номенклатуры».
- Контрагент. Элемент справочника «Контрагенты».
- Договор. Элемент справочника «Договоры контрагентов».
- Назначение. Элемент справочника «Назначения».
Номенклатура. Справочник «Номенклатура».
Справочник «Номенклатура» предназначен для хранения следующих типов номенклатуры.
Характеристика. Справочник «Характеристики номенклатуры».
В справочнике «Характеристика номенклатуры» хранится список характеристик (цвет, вес, размер и т.п.), по которым в программе можно вести дополнительный количественный учет номенклатуры.
Раздел учета. Перечисление «Разделы учета себестоимости товаров».
- Товары на складах.
- Товары переданные на комиссию.
- Производственные затраты. В ут11.0 отсутствует.
Видео:Математика это не ИсламСкачать

3. Центры затрат в 1с 8.2 ут 11
Рассмотренные 6 измерений, 6 аналитик являются аргументами функции себестоимости
В общем случае в компании может быть несколько организаций, несколько складов, огромное количество номенклатуры и т.д. Это означает, что себестоимость одного и того же товара может быть разной на разных складах, в разных организациях, с разными характеристиками и т.д. Другими словами каждый аргумент этой функции может обладать несколькими значениями:
А это означает, что количество неизвестных себестоимостей определяется совокупностью разных значений аналитик. Эти совокупности можно назвать центрами затрат:
Выше мы уже отмечали, что неизвестные значения себестоимости оцениваются путем решения системы линейных уравнений, СЛУ. Для того чтобы СЛУ имела решение, количество независимых уравнений в ней должно равняться количеству неизвестных себестоимостей. Приведем примеры подсчета необходимого количества уравнений.
Самый тривиальный случай: в компании имеется только одна организация, один склад и одно наименование товара. Это означает, что имеется только одна себестоимость
Очевидно, что для нахождения одной неизвестной себестоимости, достаточно составить одно линейное уравнение баланса.
В компании одна организация, два склада и два наименования товара. В этом случае нам понадобятся уже четыре себестоимости
Наличие только одного значения какого-либо аргумента (аналитики) равносильно тому, что себестоимость не зависит от этого аргумента. По этой причине в списке аргументов опущен аргумент «Орг». Обратите также внимание и на то, что последовательность аргументов не имеет значения. Иначе говоря
На нашем предприятии есть две организации, два склада и два наименования товара. В этом случае понадобится уже восемь себестоимостей
Для их определения необходимо составить 8 линейных уравнений. В терминах теории графов каждая триада образует свой центр формирования себестоимости, центр затрат. Таких центров затрат в данной задаче восемь:
Конечно, нет необходимости каждый раз вручную составлять эти комбинации и подсчитывать их количество. Для этой цели можно воспользоваться так называемой основной формулой комбинаторики. Пусть имеется k групп элементов, причем i-я группа состоит из n_i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением
В последнем примере было три группы элементов: организации, склады и товары. В каждой группе по два элемента. Применяя эту формулу, можем сразу вычислить количество необходимых уравнений: 8=2*2*2.
В реальной жизни на торговом предприятии достаточно много аналитик. Главным образом за счет номенклатуры. Например, предприятие включает в себя 3 организации, 4 склада и 100 наименований товаров. Очевидно, для расчета себестоимости понадобиться составить систему из 1200 линейных уравнений. И это еще не все. В ут11 есть еще три аналитики, в разрезе которых рассчитывается себестоимость. Это характеристики номенклатуры, разделы учета и виды запасов. Если каждое из них может обладать всего лишь двумя значениями, то количество уравнений возрастает до 9600.
Очевидно. Что никто из нас не будет составлять вручную СЛУ и решать ее. Это за нас сделает программа 1с 8.2 ут11. Нам же важно понимать, как она это делает.
Регламентный документ «Расчет себестоимости товаров» позволяет рассчитать себестоимость товара в 1с 8.2 редакции 11.1 одним из трех способов.
- Средняя за месяц.
- ФИФО (взвешенная оценка).
- ФИФО (скользящая оценка). Этот вариант появился в ред. 11.1.
Видео:Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

4. РАУЗ – Средняя за месяц
Составление системы линейных уравнений по методу «РАУЗ – Средняя за месяц» является более простым и наглядным, чем по методу «ФИФО (взвешенная оценка)». Хотя в общем и в том и в другом случае для каждого центра затрат записывается уравнение баланса вида
Различие в определении левой части уравнения – себестоимость остатка товаров на конец текущего периода.
Пример 4. Одна организация, один склад и один товар.
Будем считать, что на начало месяца не было остатков товара. Затем организация приобрела 10 единиц товара по цене 1000 рублей за шт. Спустя некоторое время 4 единицы этого товара были проданы. На конец месяца осталось 6 шт.
В данном примере и без решения очевидно, что себестоимость единицы товара равна 1000 рублей. Но нам важно понять, как составить уравнение и расчетным путем получить это значение.
Так как у нас одна организация, один склад и один товар, то количество уравнений, которые нам необходимо составить, одно: 1=1*1*1.
Легко подсчитать, что на конец месяца осталось 6 единиц товара. Себестоимость единицы товара неизвестная величина, обозначим ее за x. Умножив на нее количественный остаток, получим себестоимость остатка товара на конец текущего месяца, то есть 6x. За месяц поступлений было на 10000 рублей. Четыре единицы товара были проданы. Себестоимость их списание равна 4x . Очевидно уравнение баланса будет иметь вид
Здесь x это неизвестная себестоимость единицы товара. Не путать с продажной стоимостью товара. Из этого уравнение легко найдем, что
Позже мы увидим, что программа 1с ут 11 в отчетах отображает не стоимость единицы товара, а себестоимость выбытия товара и себестоимость остатка товара. В нашем случае это 4000 руб. и 6000 руб. соответственно.
Пример 5. Одна организация, два склада и один товар.
Будем считать, что на начало января на складах организация ООО «ТоргБыт» не было остатков товара. Имели место следующие операции.
- 14.01.2013. приобретено за плату 10 вентиляторов по цене 1000 рублей за шт. и они были оприходованы на Склад-А.
- 15.01.2013. приобретено за плату 20 вентиляторов по цене 2000 рублей за шт. и они были оприходованы на Склад-Б.
- 19.01.2013. со Склада-Б на Склад-А перемещено 15 вентиляторов.
- 20.01.2013. продано 4 вентилятора по цене 3000 рублей за штуку.
Себестоимости вентиляторов на Складе-А и Складе-Б разные. Обозначим их, как x_А и x_Б соответственно. На конец месяца на Складе-А осталось 21 единица товара, а на Складе-Б 5 единиц товара. Обратите внимание, со Склада-Б товары перемещаются по неизвестной пока нам себестоимости x_Б на Склад-А. А со Склада-А они списываются по себестоимости x_А.
Количество уравнений, которые нам необходимо составить равно двум: 1*2*1=2. Так как организация у нас одна и товар один, то себестоимость товара по этим аналитикам не различается. Остается только одна аналитика «Склады» с двумя значениями: Склад-А и Склад-Б. В данном примере центры затрат свелись к двум складам. Для каждого значения этой аналитики, иначе для каждого центра затрат, запишем свое уравнение баланса.
Уравнение баланса для Склада-А:
Уравнение баланса для Склада-Б:
Наверное, у читателя возник вопрос, почему, определяя себестоимость методом решения СЛУ, тем не менее, этот метод называют «Средняя за месяц». Более того. Это не просто средняя за месяц, а средняя взвешенная оценка себестоимости за месяц. Да потому, что решение СЛУ сводится к оценке
А это и есть формула для расчета средней взвешенной оценки.
Решая полученную систему, найдем, что x_Б=2000, а x_А=1600. Правда, в отчете «Анализ себестоимости товаров» мы не увидим себестоимости единицы товара. Впрочем, давайте по порядку. После расчета фактической себестоимости в отчете «Анализ себестоимости товаров» отразятся следующие результаты.
Легко догадаться, что 25 вентиляторов, поступивших на Склад-А, это сумма, образованная за счет покупки 10 вентиляторов и 15 перемещенных со Склада-Б вентиляторов. Значение 40000 рублей это просто стоимость закупки данных вентиляторов: 10*1000+15*2000=40000 рублей. К этому выводу можно прийти, получив расшифровку по строке «Склад-А».
Себестоимость 4 вентиляторов, реализованных со Склада-А равна 6400=4*1600. Это совпадает с нашим расчетом. На конец месяца осталось 25-4=21 вентилятор. Их себестоимость составляет 21*1600=33600 рублей.
На Склад-Б вентиляторы поступили только однажды. Поэтому их фактическая себестоимость равна стоимости покупки. Это видно было из нашего расчета. Этот же результат показывает и отчет «Анализ себестоимости товаров» по Складу-Б.
Забегая вперед, приведем следующие оценки для 4 реализованных вентиляторов.
- РАУЗ – Средняя за месяц. 6400 руб.
- РАУЗ – ФИФО (взвешенная оценка). 4000 руб.
- РАУЗ – ФИФО (скользящая оценка). 4000 руб.
Пример 6. Одна организация, один склад, один товар и остаток на начало месяца.
Особенность этого примера состоит в том, что среди аналитик себестоимости есть вид запасов. Значениями этой аналитики являются элементы справочника «Виды запасов». При вводе остатков на начало учета в этом справочнике будет создан элемент «Собственный товар». В дальнейшем при покупке новой партии товара, например, у поставщика База «Электроника и бытовая техника» будет создан элемент «Собственный товар: База «Электроника и бытовая техника»».
Получается два значения аналитики. Значить себестоимость должна рассчитываться для двух значений вида запаса:
- Собственный товар,
- Собственный товар: База «Электроника и бытовая техника».
Проверим это предположение на следующем примере.
- 31.12.2012. На эту дату на Склад-А в организации ООО «ТоргБыт» документом «Ввод начальных остатков» введем 10 холодильников по цене 1000 рублей за штуку.
- 14.01.2013 документом «Поступление товаров и услуг» зарегистрирована покупка 100 холодильников по цене 2000 рублей за штуку, и они оприходованы на Склад-А.
- 21.01.2013 документом «Реализация товаров и услуг» зарегистрирована продажа 70 холодильников по цене 3000 рублей за штуку на сумму 210000 рублей.
В данном разделе мы рассматриваем метод «РАУЗ – Средняя за месяц», а не ФИФО. Тем не менее, разумно предположить, что программа сначала спишет 10 холодильников из остатка, затем еще 60 холодильников из вновь поступившей партии. Тогда для вида запаса «Собственный товар» схема и уравнение будут такими.

Для вида запаса «Собственный товар: База «Электроника и бытовая техника»» чуть сложнее.

Легко видеть, что по виду запаса «Собственный товар» себестоимость списанных товаров равняется
А себестоимость списанных товаров по виду запаса «•Собственный товар: База «Электроника и бытовая техника»» составляет
Итого списано на 130000 рублей. Сформируем отчет «Анализ себестоимости товаров» в разрезе видов запасов. Относительно начального остатка и прихода все очевидно.
На следующем фрагменте мы действительно видим, что первые 10 холодильников списаны из вида запаса «Собственный товар». А остальные 60 из вида запаса «Собственный товар: База «Электроника и бытовая техника»».
Здесь в некотором смысле можно говорить о ФИФО. Остатки списываются по методу ФИФО, а остальные товары по себестоимости, рассчитанной путем решения СЛУ.
Пример 7. Остатки товаров образовались за счет нескольких партий.
В текущей деятельности остатки товаров на начало текущего месяца могут принадлежать разным партиям. Возникает вопрос, как они будут учитываться в расчете себестоимости реализованных товаров. Рассмотрим следующий пример.
- 30.01.2013. на Склад-А организация купила 10 пылесосов «Электросила» по цене 1000 рублей за единицу на сумму 10000 рублей.
- 31.01.2013. на Склад-А организация купила 40 пылесосов «Электросила» по цене 500 рублей за единицу на сумму 20000 рублей.
- 01.02.2013. организация продала 20 пылесосов «Электросила» по цене 2000 рублей за единицу на сумму 40000 рублей.
Если предположить, что себестоимость единицы остатка рассчитывается по формуле средневзвешенной оценки, то получим, что
Это правильный результат, ибо отчет «Анализ себестоимости товаров», что себестоимость выбытия 20 пылесосов равен 20*600=12000 рублей, а стоимость остатка на конец текущего месяца равна 30*600=18000 рублей.
Пример 8. Одна организация, два склада и два товара.
Рассмотрим более сложный пример и отразим его в программе 1С:Управление торговлей ред. 11.1
- 01.01.2013. на Склад-А организация купила 100 телевизоров по цене 2000 рублей за единицу на сумму 200000 рублей.
- 02.01.2013. на Склад-Б организация купила 100 кофеварок по цене 1500 рублей за единицу на сумму 150000 рублей.
- 03.01.2013. на Склад-Б организация купила 140 телевизоров по цене 3000 рублей за единицу на сумму 420000 рублей.
- 04.01.2013. со Склада-Б на Склад-А перемещено 30 кофеварок.
- 05.01.2013. на Склад-А организация купила 200 кофеварок по цене 1800 рублей за единицу на сумму 360000 рублей.
- 06.01.2013. со Склада-Б на Склад-А перемещено 60 телевизоров.
- 07.01.2013. со Склада-А на Склад-Б перемещено 120 кофеварок.
- 08.01.2013. со Склада-А реализовано 70 телевизоров по цене 5000 рублей за штуку на сумму 350000 рублей.
- 09.01.2013. со Склада-А на Склад-Б перемещено 10 телевизоров.
- 10.01.2013. со Склада-Б реализовано 50 кофеварок по цене 3000 рублей за штуку на сумму 150000 рублей.
- 11.01.2013. со Склада-А реализовано 100 кофеварок по цене 3000 рублей за штуку на сумму 150000 рублей.
Красные номера на рисунке отражают дату ввода документа.
Так как у нас одна организация, два склада и две номенклатуры, то количество уравнений, которые нам необходимо составить, будет четыре: 4=1*2*2. Одна организация означает, что по данной аналитике себестоимость не различается. Это равносильно тому, что такой аналитики, как организация, просто нет. Осталось две аналитики: Склад и Номенклатура.
Для каждой аналитике в нашем примере существует по два значения. Следовательно, нам необходимо рассчитать 4 себестоимости, а для этого следует составить 4 уравнения. Уравнение баланса составляем для каждой пары значений аналитики. Их можно назвать центрами затрат:
Суммовой остаток телевизоров на конец месяца на Складе-А описывается уравнением баланса для центра затрат (Склад-А, Телевизоры)
Суммовой остаток кофеварок на конец месяца на Складе-А описывается уравнением баланса для центра затрат (Склад-А, Кофеварки)
Суммовой остаток телевизоров на конец месяца на Складе-Б описывается уравнением баланса для центра затрат (Склад-Б, Телевизоры)
Суммовой остаток кофеварок на конец месяца на Складе-Б описывается уравнением баланса для пары (Склад-Б, Кофеварки)
Из этой системы линейных уравнений легко найдем следующие значения.
Себестоимость 80 отгруженных и перемещенных со Склада-А телевизоров, а также себестоимость 80 оставшихся на Складе-А телевизоров равна
Такой же результат показывает и отчет «Анализ себестоимости товаров».
Себестоимость 60 отгруженных и перемещенных со Склада-Б телевизоров, а также себестоимость 90 оставшихся на Складе-Б телевизоров равна:
Такой же результат показывает и отчет «Анализ себестоимости товаров».
Себестоимость 80 отгруженных и перемещенных со Склада-Б кофеварок, а также себестоимость 140 оставшихся на Складе-Б кофеварок равна
Такой же результат показывает и отчет «Анализ себестоимости товаров».
Себестоимость 220 отгруженных и перемещенных со Склада-А кофеварок, а также себестоимость 10 оставшихся на Складе-А кофеварок равна
Такой же результат показывает и отчет «Анализ себестоимости товаров».
Забегая вперед, приведем следующие оценки для себестоимости списания 80 телевизоров со Склада-А.
- РАУЗ – Средняя за месяц. 187717,90 руб.
- РАУЗ – ФИФО (взвешенная оценка). 160000 руб.
- РАУЗ – ФИФО (скользящая оценка). Нуль рублей.
Меня тоже удивил последний результат. Хотя по теории должно быть 160000 руб. Покопавшись в конфигурации, нашел обработку «Первоначальное заполнение регистров партионного учета» и запустил ее. После этого все встало на свои места.
Видео:Решение системы уравнений методом ГауссаСкачать

5. Граф затрат
Приведенные выше схемы наглядны для пользователя, да и то в предельно простых случаях. Организовать же на их основе автоматизацию расчета невозможно. На самом деле программа автоматически определяет количество центров затрат, строит соответствующий граф. Затем формируется система уравнений и регламентными документами производится расчет себестоимости.
Покажем, как составить граф затрат и СЛУ для примера 5. Здесь два склада и два товара. Значить количество неизвестных себестоимостей четыре. Совокупности аргументов этих себестоимостей образуют четыре узла графа. В данном контексте их называют центрами затрат:
Для краткости использованы обозначения: А это Склад-А, Б – Склад-Б, Тв – телевизоры, Кф – кофеварки.
Каждый центр затрат взаимодействует с остальными центрами. В общем случае данный граф будет выглядеть, как на рисунке. Цифрами обозначены номера центров затрат.
Дуги между узлами показывают величину и направление затрат. Например, дуга, направленная от узла 1 к узлу 2 означает, что какое-то количество телевизоров перемещено со Склада-А на Склад-Б. Возможны и обратные потоки. Собственно все красные дуги это возможные перемещения между складами.
Зеленые дуги от поставщиков товара к узлам затрат обозначают затраты, обусловленные покупкой и оприходованием товаров в соответствующий центр затрат. Исходящие из центров затрат синие дуги обозначают списание себестоимости при продаже товаров покупателям.
При внимательном рассмотрении графа придем к выводу, что некоторые дуги не обладают содержательным смыслом. Например, что может означать дуга, направленная, от узла 1 к узлу 3. Телевизоры, перемещенные внутри Склада-А, превратились в кофеварки? Такого в реальности быть не может.
Впрочем, чисто теоретически телевизоры можно переделать в кофеварки. Соответственно они будут обладать уже другой себестоимостью. Однако наша организация такими операциями не занимается.
Поэтому в графе затрат удаляем все дуги, которые не отражают реальных потоков затрат. Одновременно учтем, что на начало месяца на любом складе могут существовать остатки товаров.
Уравнение баланса для первого центра затрат представим с пояснениями

Видео:Лекция 12. Системы линейных уравненийСкачать

6. РАУЗ – ФИФО (взвешенная оценка)
Метод «РАУЗ – ФИФО (взвешенная оценка)» отличается от метода «РАУЗ – Средняя за месяц» лишь методом формирования левой части уравнения. То есть методом определения суммового остатка товаров на конец месяца.
- РАУЗ – Средняя за месяц. Суммовой остаток товаров на конец месяца мы определяли, как количество товаров, умноженное на неизвестную себестоимость.
- РАУЗ – ФИФО (взвешенная оценка). Суммовой остаток товаров на конец месяца определяется методом ФИФО.
Правая часть уравнений СЛУ формируется одинаковым способом для обеих методов. Рассмотрим характерные примеры.
Пример 9. Учет партий прошлого месяца.
В течение прошлого месяца поступили несколько партий товара. Однако не все товары из этих партий были реализованы. Возникает вопрос, как программа учитывает в текущем месяце эти партии при расчете себестоимости? Для ответа на этот вопрос рассмотрим следующий пример.
- 30.01.2013. на Склад-А организация купила 10 пылесосов «Электросила» по цене 1000 рублей за единицу на сумму 10000 рублей.
- 31.01.2013. на Склад-А организация купила 40 пылесосов «Электросила» по цене 500 рублей за единицу на сумму 20000 рублей.
- 01.02.2013. организация продала 20 пылесосов «Электросила» по цене 2000 рублей за единицу на сумму 40000 рублей.
В ред. 11.0 все остатки прошлых месяцев по какой-то причине объединялись в одну партию. При этом себестоимость одной единицы рассчитывалась по формуле средневзвешенной оценки
В этом случае себестоимость выбытия для нашего примера составит 20*600=12000 рублей, а стоимость остатка 30*600=18000 рублей.
В ут11.1 ситуация исправлена. Партии прошлого месяца не объединяются в одну партию: списание производится методом ФИФО.
Из 20 реализованных товаров 10 единиц взяты из первой партии (10*1000=10000). Остальные 10 товаров из второй партии (10*500=5000). Итого себестоимость списания 20 единиц товара составит 15000 рублей. Остаток 30*500=15000 рублей.
Именно этот результат и отображает отчет «Анализ себестоимости товаров».
Такой подход представляется более обоснованным. И он означает, что в ут11.1 появились партии.
Пример 10. Себестоимость остатка на конец периода.
Перед тем, как сформировать уравнения программа рассчитывает себестоимость остатка товаров на конец периода методом ФИФО.
Себестоимость остатка товаров на конец периода рассчитывается методом ФИФО, как разность между себестоимостью всех поступивших партий и себестоимостью отгруженных первых партий.
Это прямое следствие метода ФИФО. Суммовой остаток товаров на конец периода определяется стоимостью последних партий. Поясним сказанное на примере.
- 04.02.2013. на Склад-А организация купила 10 комодов по цене 1000 рублей за единицу на сумму 10000 рублей.
- 05.02.2013. на Склад-А организация купила 20 комодов по цене 2000 рублей за единицу на сумму 40000 рублей.
- 06.02.2013. на Склад-А организация купила 15 комодов по цене 3000 рублей за единицу на сумму 45000 рублей.
- 11.02.2013. организация продала 15 комодов по цене 4000 рублей за единицу на сумму 60000 рублей.
При отгрузке программа списала 10 комодов из 1-й партии товара и 5 комодов из 2-й партии. Следовательно, суммовой остаток будет сформирован из себестоимости оставшихся 15 штук товара 2-й партии и 15 штук товара 3-й партии, то есть 15*2000+15*3000=75000 руб.
Другими словами 75000 рублей это себестоимость оставшихся на конец периода 30 штук товара. Уравнение для себестоимости будет иметь следующий вид
Откуда найдем, что себестоимость реализованных товаров равняется
Этот результат подтверждается отчетом «Анализ себестоимости товаров».
Пример 11. Перемещения с одного склада на другой.
В ред. 11.0 при подсчете суммового остатка товаров на конец месяца почему-то не учитывалась себестоимость перемещенных на данный склад товаров. В редакции 11.1 эта ситуация исправлена. При подсчете суммового остатка в качестве себестоимости перемещенного товара программа принимает его стоимость из партии его поступления. Поясним это на примере.
- 04.02.2013. на Склад-А организация купила 10 комодов по цене 1000 рублей за единицу на сумму 10000 рублей.
- 05.02.2013. на Склад-Б организация купила 15 комодов по цене 3000 рублей за единицу на сумму 45000 рублей.
- 06.02.2013. со Склада-Б на Склад-А перемещено 10 комодов.
- 07.02.2013. на Склад-А организация купила 20 комодов по цене 2000 рублей за единицу на сумму 40000 рублей.
- 08.02.2013. на Склад-А организация купила 15 комодов по цене 3000 рублей за единицу на сумму 45000 рублей.
- 11.02.2013. организация продала 15 комодов по цене 4000 рублей за единицу на сумму 60000 рублей.
При подсчете суммового остатка надо как-то учитывать и товар, который появился на данном складе за счет перемещения с другого склада. Так на рисунке мы видим, что между поступлением 3-й партии и отгрузкой 15 штук товара имело место перемещение товара в количестве 10 штук со Склада-Б на Склад-А.
Легко подсчитать количество комодов на конец текущего месяца: 10+10+20+15-15=40. Подсчитаем их суммовой остаток.
При реализации 15 комодов 10 комодов списаны из 1-й партии. В этой партии ни одного комода не осталось. Оставшиеся 5 комодов списываются из перемещенной со Склада-Б партии. В качестве стоимости перемещенных товаров естественно указать стоимость товаров из этой партии, то есть 3000 рублей за комод.
Следовательно, суммовой остаток на Складе-А на конец месяца будет равен
Обратите внимание, что в правой части уравнения себестоимость перемещенных со Склада-Б на Склад-А комодов предполагается неизвестной. Решая эти уравнения, найдем
Этот результат подтверждается расчетом в ут11.1.
Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

7. РАУЗ – ФИФО (скользящая оценка)
Такого метода в ут11.0 не было. Для его реализации в конфигурации созданы соответствующие регистры накопления партионного учета. В частности документы поступления, списания и перемещения товаров делают записи в регистре накопления «Партии товаров организаций».
При использовании этого метода похоже на то, что СЛУ не формируется и себестоимость списанных товаров определяется обычным методом ФИФО.
Однако этот метод предполагает, чтобы все партии были проведения в хронологической последовательности. В этом поможет новая обработка «Закрытие месяца». В числе прочих операций она восстанавливает последовательность проведения партий.
Однако этих очевидных операций не достаточно. Если, принято решение рассчитывать себестоимость методом «РАУЗ – ФИФО (скользящая оценка)», то предварительно обязательно заполните регистры партионного учета начальными сведениями. Это делается одноименной обработкой «Первоначальное заполнение регистров партионного учета».
Видео:1С:ERP Урок 68. Расходы предприятия. СебестоимостьСкачать

8. Отрицательные остаткив 1с 8.2 ут11
Неприятной особенностью конфигурация ут11.0 было то, что она неправильно рассчитывала себестоимость товаров при наличии отрицательных остатков.
С чем это связано. Обычно в начале внедрения программы ей разрешают проводить документы без контроля остатков. В ут 11 тоже есть такой механизм, но он эффективнее, чем в ред. 10.3.
В разделе «АДМИНИСТРИРОВАНИЕ / Финансы» (в ред. 11.1 АДМИНИСТРИРОВАНИЕ / Организации и финансы) есть флаг «Контролировать остатки товаров организаций». Его установка обеспечит контроль остатков во всех организациях и на всех складах. А вот, если этот флаг снят, то способ контроля остатков определяется значением поля «Вариант контроля остатков» в карточке соответствующего склада.
Проверим, как реагируют ут11.0 и ут11.1 на отрицательные остатки при расчете себестоимости на следующем примере
- 21.01.2013. на Склад-А организация купила 10 метров «Кабеля NYM (Севкабель) 5х35» по цене 1000 рублей за единицу на сумму 10000 рублей.
- 28.01.2013. продано 15 метров «Кабеля NYM (Севкабель) 5х35» на сумму 30000 рублей.
Предварительно снимите флаг «Контролировать остатки товаров организаций» и для склада Склад-А установите вариант «Не контролировать».
Очевидно, что на конец месяца получится отрицательный остаток: -5 единиц товара. Уравнение баланса при этом будет иметь вид
Из него легко найдем, что
Соответственно себестоимость списания отгруженных товаров должна равняться 15000 рублей. Однако расчет в ред. 11.0 покажет, что себестоимость 15-ти отгруженных товаров равна не 15000 рублей, а 10000 рублей.
При расчете себестоимости, например, по методу «РАУЗ – Средняя за месяц» программа, тем не менее, сообщит, что нарушена последовательность проведения партионного учета. Восстановление производится обработкой «Закрытие месяца».
При ее запуске она обнаружит отрицательные остатки и предложит исправить их. До тех пор, пока не будут оформлены недостающие товары, программа не позволит рассчитать себестоимость.
Видео:Совместные и несовместные, определенные и неопределенные системы линейных уравненийСкачать

Заключение
В программе 1С:Управление торговлей редакция 11.1 на выбор пользователю предоставлено три варианта расчета себестоимости.
- Средняя за месяц.
- ФИФО (взвешенная оценка).
- ФИФО (скользящая оценка).
Любой из них обеспечивает достаточно корректный способ расчета себестоимости. И, тем не менее, наличие вариантов, заставляет пользователя задуматься над выбором подходящего для него варианта.
Прежде, чем ответить на этот вопрос, заметим, что из ведра можно вылить ровно столько воды, сколько мы в него налили. Так и с себестоимостью. Не важно, как много партий товаров поступало в течение нескольких месяцев. Важно, что при любом методе расчета себестоимости списанная себестоимость, после того, как будут распроданы все товары, должна быть равной стоимости их закупок с учетом возможных транспортно-заготовительных расходов.
Однако от месяца к месяцу эти оценки могут колебаться. Следовательно, метод оценки себестоимости важен лишь для оперативной оценки финансового результатам по данным конкретного месяца. Поэтому при выборе метода оценки следует учитывать следующие критерии.
Точность. Абсолютно точным является метод «ФИФО (скользящая оценка)»: по какой стоимости купили, по такой и списали. Часто результат оценки себестоимости методом «ФИФО (взвешенная оценка)» могут совпадать с оценкой по методу «ФИФО (скользящая оценка)».
Производительность. В методе «Средняя за месяц» партии не используются. Поэтому он обеспечивает наивысшую производительность системы. В методе «ФИФО (взвешенная оценка)» используется информация об остатках партий предыдущего месяца. Поэтому по производительности его можно поставить на второе место после метода «Средняя за месяц».
Самым «медлительным» является метод «ФИФО (скользящая оценка)». Крупным торговым организациям его можно рекомендовать, если в них предприняты технические средства повышения производительности системы.
Отдельно стоит остановиться на небольших торговых организациях. Для них производительность работы системы при любом методе оценки практически будет одинакова. Поэтому пользователь такой базы выбирает тот метод, который для него более привычен и удобен.
К сожалению, не существует критерия с точки зрения расчета себестоимости, по которому одну организацию можно назвать очень крупной, а другую маленькой. Дело в том, что производительность системы определяется не только программным обеспечением, но и техническими средствами.
Поэтому можно попробовать рассчитать себестоимость разными методами и выбрать для себя наиболее подходящий метод.
Удобство использование. Наиболее удобным представляется метод «Средняя за месяц». Не надо предварительно запускать обработку «Первоначальное заполнение регистров партионного учета». Не надо перед каждым расчетом себестоимости восстанавливать последовательность партий. Документы можно проводить в любом порядке.
Видео:Решение систем линейных уравнений методом Гаусса.Скачать

Чтобы еще почитать?
Программа 1С:Управление торговлей версии 11.1.1.11 вышла 28.02.2013. Технические писатели фирмы 1С напряженно переписывают ранее выпущенные руководства. Прежние книги для работы с ут11.1 практически бесполезны. То есть на момент выхода этой версии литературы нет. Поэтому решил поделиться полезными ссылками.
Это статьи финалистов курса 1С:Управление торговлей – Быстрый старт: Затраты, Себестоимость, Финансы. Финалисты это те слушатели, которые выполнили все домашние задания и отчитались по ним. Разработчики курса Фарит Насипов и Евгений Гилев предложили им написать статьи про ут11. Тридцать человек приняли это приглашение. Авторы трех статей стали призерами конкурса статей.
1-е место. Что же такое «Интеркампани»?, Голиков Александр Борисович. Хотите узнать, что такое Интеркампани? Тогда эта статья будет вам полезной. Рассмотрены принципы работы, особенности настройки и применения.
2-е место. Впечатления от знакомства с УТ11. Мое первое знакомство с УТ11 или «если вам не нравится, то вы просто не умеете ее готовить».
3-е место. Работа на адресном складе. Артемов Артем Владимирович. Принципы работы адресного склада. Процесс настройки склада. Ввод начальных остатков. Оформление приемки и отгрузки.
Эта статьи, набравшие наибольшее количество голосов. Но это не означает, что остальные статьи недостойны внимания. Вот еще несколько ссылок. Они отражают исключительно мой интерес. Возможно, это будет интересно и вам.
Работа с контрагентами в УТ 11. Организация работы с контрагентами в УТ 11. Разделение на контрагенты и партнеры. Пример организации работы с сетью.
Настройка серий в 1С:Управление Торговлей 11. Бейдик Елена . Эта статья может быть полезна людям, которые не любят читать инструкции. Поможет быстро настроить возможность учёта товаров в разрезе серий в системе 1С:Управление Торговлей 11.
10 шагов сборки – через тернии к себестоимости. . В статье рассматривается методика и бизнес-процесс учета сборки оборудования на примере системных блоков. Будет интересно тем, кто хочет узнать как можно рассчитать себестоимость единицы товара, а также зачем нужны статусы документов «Заказ клиента», «Заказ на сборку», «Сборка товаров».
Приходуем Товар – на «Склад» или в «Помещение»?! Павел Ванин. Статья повествует о новшествах, коснувшихся в Управление торговлей 11 понятия «Склады». Рассмотрен один из частых случаев организации складского учета на предприятии и выбрана подходящая структура справочника «Склады» в программе. Статья позволит избежать одни из «грабель» при внедрении УТ 11.
Основные настройки, особенности работы, проблемные ситуации и ошибки в УТ 11.0, важные для расчеты себестоимости. Жукова Наталья Алексеевна . Статья описывает основные настройки, особенности поведения системы, ее проблемные места. Все это взято из материалов курса, обсуждений на сайте и скомпилировано в одном месте. Поэтому центральное место здесь занимает описание особенностей расчета себестоимости. Понимание особенностей работы системы позволит совершать меньше ошибок. По проблемам, по возможности, предлагается решение. Здесь то, что необходимо знать внедренцу, руководителю, главному бухгалтеру о программе перед началом внедрения, есть интересная информация и для пользователя. Хочу обратить внимание, что статья написана не с целью поругать УТ11.0. Хочется, чтобы было понимание, что может и что не может система, как правильно работать с ней и какие у нее особенности.
Работа с платежными картами в конфигурации Управление торговлей 11. Григорьев Александр Николаевич. Уважаемые коллеги! Это моя первая статья, так что не судите строго. Как говориться – проба пера. Я долго думал, про что написать и решил осветить тему продаж с помощью банковских карт. Итак, начнем. Все понимают, что речь пойдет о розничных продажах. Чтобы работать с розницей, необходимо в программе настроить соответствующие параметры учета (Администрирование – Продажи …
Способ оценки товаров при выбытии: ФИФО, Среднее, РАУЗ и УТ 11. Статья о том, что в любой сфере деятельности требуется проявление поиска, творческого подхода, нового взгляда на предметы своей деятельности и окружающий мир. Придумывать, пробовать, искать и находить новые неизученные, неизведанные возможности и способы решения себе же самому, поставленных задач.
«Вечная Хлебопечка» или история одной сборки товаров. . В самом начале представлю задачу, с которой я столкнулся в процессе прохождения данного курса. Представьте себе, что Вы собираете комплект для продажи: вы оприходовали составные части, задали номенклатуру-комплект и спецификацию для неё. Следующим шагом логично будет проведение документа сборки (разборки) товаров. Вы пытаетесь его провести и видите такую ошибку: (Нажмите, чтобы увеличить картинку) Ничего страшного, …
Учет товарных бонусов в УТ 11.0.9 или на халяву и уксус сладкий. В этой статье описывается альтернативный взгляд на учет бонусных позиций которые организация предоставляет покупателям при различных товарных акциях. Я попробовал описать личный опыт работы с бонусами в программах 1С. В статье описан методика работы без изменения конфигурации. Если будет интересно, выложу, работающую на реальном предприятии методику по учету натуральных бонусов, но которая уже требует внесение доработок в программу.
Видео:Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Решение системы линейных уравнений
Начиная с версии платформы 8.3.14.1565 в 1С:Предприятие стал доступен объект для решения системы линейных уравнений. Следует предположить, что данный функционал не вызвал значительного интереса, так как я не нашел на infostart ни одного упоминания, относящегося к данному предмету. Поиск через Яндекс вывел на статью «Механизм решения систем линейных алгебраических уравнений», которая всем хороша, за исключением того, что не содержит примера применения нового класса РасчетСистемЛинейныхУравнений. Этот пробел я и постараюсь восполнить. Решать будем систему из трех уравнений, которая вынесена в заголовок статьи.
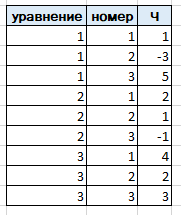
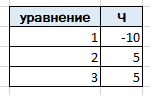
На первом шаге подготовим две таблицы значений. В одной будем хранить коэффициенты из левой части, а в другой свободные члены системы уравнений.
Каждая из таблиц содержит колонку уравнение, в которой указывается номер уравнения , а так же колонку Ч, в которую заносятся значения коэффициентов. Кроме этого, таблица с коэффициентами из левой части решаемой системы содержит колонку номер, для указания номера переменной, к которой относится данный коэффициент. Упростим себе жизнь и и напишем две процедуры для заполнения данных таблиц.
Теперь выполним подготовительные процедуры.
На следующем шаге переходим к работе с объектом РасчетСистемЛинейныхУравнений. У него есть два свойства, первое — ИсточникДанныхУзлов, через которое передаются значения свободных коэффициентов, и свойство ИсточникДанныхСвязей для передачи значений коэффициентов из левой части системы линейных уравнений. Отметим, что кроме сформированных таблиц мы указываем имена колонок, в которых хранится номер уравнения и номер переменной.
Заключительный штрих. Для того чтобы все заработало надо добавить ОписанияСистемЛинейныхУравнений в коллекцию ОписанияСистем класса РасчетСистемЛинейныхУравнений.
И наконец непосредственный расчет.
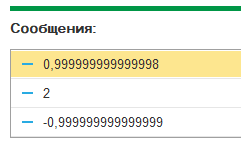
Точное решение для данной системы :
Убедиться в этом можно непосредственной подстановкой. Программа дает ответ с некоторой точностью, что обусловлено применяемым итерационным алгоритмом.
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Ваш браузер устарел, пожалуйста обновите ваш браузер пройдя по ссылке www.microsoft.com/download

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Решение СЛАУ на примере распределения транспортных расходов.
Допустим, организация ведет учет транспортных расходов отдельно от стоимости перевозимых товаров.
Весь учет ведется в некотором регистре остатков
— Количество (количество перевезенных товаров)
— Сумма (сумма понесенных транспортных расходов)
Транспортные расходы возникают при проведении документа «Расходный ордер на товары»
Сумму транспортных расходов нужно распределять по некоторым операциям, например:
Распределение производится за месяц последним днем месяца.
Представим операции за период в виде схемы.
. и в виде таблицы.
Остатки на начало периода: Сумма — остаток нераспределенных транспортных расходов, Количество — остаток товара на складе.
| Период | Склад | Количество | Сумма ТР |
| 01.07.2014 | А | 100 | 1000 |
| 01.07.2014 | Б | 150 | 1500 |
| 01.07.2014 | В | 120 | 1600 |
| 01.07.2014 | Г | 90 | 1900 |
Операции, на которые нужно распределить сумму ТР:
| Период | Документ | Операция | Склад отпр | Склад получ | Количество | Сумма ТР |
| 05.07.2014 | Расходный ордер №1 | Перемещение | А | Б | 20 | 800 |
| 10.07.2014 | Расходный ордер №2 | Перемещение | Б | В | 40 | 1000 |
| 11.07.2014 | Комплектация номенклатуры №1 | Комплектация | Г | 60 | ||
| 12.07.2014 | Расходный ордер №3 | Перемещение | В | Г | 50 | 1200 |
| 13.07.2014 | Комплектация номенклатуры №2 | Комплектация | Г | 40 | ||
| 16.07.2014 | Расходный ордер №4 | Перемещение | Г | А | 20 | 600 |
| 17.07.2014 | Передача товаров №1 | Переработка | В | 15 | ||
| 18.07.2014 | Поступление товаров из пер-ки№1 | Переработка | В | 20 | ||
| 20.07.2014 | Реализация товаров и услуг №1 | Реализация | А | 100 | ||
| 25.07.2014 | Реализация товаров и услуг №2 | Реализация | Б | 130 |
Решение.
В целом решение будет состоять из следующих шагов:
1. Составить таблицу движений
2. Составить таблицу СЛАУ
4. Подставить в таблицу движений полученные значения суммы ТР на единицу для каждого склада (стоимость выбытия)
1. Составляем таблицу движений
Не важно как, дополним исходную таблицу строками движений на основе операций. Должно получиться это:
| № | Период | Операция | Склад | Корр склад | Количество приход | Количество расход | Сумма ТР приход | Сумма ТР расход |
| 1 | 01.07.2014 | Сальдо | А | 100 | 1000 | |||
| 2 | 01.07.2014 | Сальдо | Б | 150 | 1500 | |||
| 3 | 01.07.2014 | Сальдо | В | 120 | 1600 | |||
| 4 | 01.07.2014 | Сальдо | Г | 90 | 1900 | |||
| 5 | 05.07.2014 | Перемещение | Б | А | 20 | 800 | ||
| 6 | 05.07.2014 | Перемещение | А | 20 | ||||
| 7 | 10.07.2014 | Перемещение | В | Б | 40 | 1000 | ||
| 8 | 10.07.2014 | Перемещение | Б | 40 | ||||
| 9 | 11.07.2014 | Комплектация | Г | 60 | ||||
| 10 | 12.07.2014 | Перемещение | Г | В | 50 | 1200 | ||
| 11 | 12.07.2014 | Перемещение | В | 50 | ||||
| 12 | 13.07.2014 | Комплектация | Г | 40 | ||||
| 13 | 16.07.2014 | Перемещение | А | Г | 20 | 600 | ||
| 14 | 16.07.2014 | Перемещение | Г | 20 | ||||
| 15 | 17.07.2014 | Переработка | В | 15 | ||||
| 16 | 18.07.2014 | Переработка | В | 20 | ||||
| 17 | 20.07.2014 | Реализация | А | 100 | ||||
| 18 | 25.07.2014 | Реализация | Б | 130 | ||||
| 19 | 31.07.2014 | Сальдо | А | 0 | ||||
| 20 | 31.07.2014 | Сальдо | Б | 0 | ||||
| 21 | 31.07.2014 | Сальдо | В | 105 | ||||
| 22 | 31.07.2014 | Сальдо | Г | 140 |
2. Составление таблицы СЛАУ
Далее нужно будет составить систему линейных уравнений баланса этой таблицы. Решив эту систему, мы сможем получить стоимость списания транспортных расходов с каждого склада.
Уравнения будут такие:
для склада А: 1000 — 20*А + 20 *Г + 600 – 100 * А = 0*А
для склада Б: 1500 + 20*А + 800 – 40*Б – 130*Б = 0*Б
для склада В: 1600 + 40 *Б + 1000 – 50*В + 15*В – 20*В = 105*В
для склада Г: 1900 + 60*Г + 50*В + 1200 – 40*Г –20*Г = 140*Г
Где множители А,Б,В,Г – это неизвестная стоимость списания ТР на единицу товара с одноименного склада.
Упростим эти уравнения, также переместив все свободные члены (без множителей) за знак равенства.
Получим такую систему уравнений:
для склада А: -120*А + 20 *Г = -1600
для склада Б: 20*А – 170*Б = -2300
для склада В: 40 *Б – 160*В = -2600
для склада Г: 50*В — 140*Г = -3100
Теперь опишем эти уравнения в виде таблицы, полученной из таблицы движений:
| № | Склад | А | Б | В | Г | Свободный член | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | А | -1000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Б | -1500 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | В | -1600 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Г | -1900 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Б | 20 | -800 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | А | -20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | В | 40 | -1000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Б | -40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Г | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Г | 50 | -1200 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | В | -50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Г | -40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | А | 20 | -600 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Г | -20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | В | 15 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | В | -20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | А | -100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Б | -130 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | А | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Б | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | В | -105 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Г | -140 |
| Склад | А | Б | В | Г | Свободный член |
| А | -120 | 20 | -1600 | ||
| Б | 20 | -170 | -2300 | ||
| В | 40 | -160 | -2600 | ||
| Г | 50 | -140 | -3100 |
Теперь эту систему нужно решить. Каким образом?
Любой метод решения СЛАУ даст результаты, разной степени точности.
Используем метод Гаусса с выделением главного элемента. Он считается самым точным, однако «при большом числе уравнений метод может стать слишком сложным».
И метод простых итераций.
Для начала нужно привести матрицу к диагональному виду, т.е отсортировать строки таким образом, чтобы на диагонали располагался максимальный по модулю элемент столбца. Это и есть «выделение главного члена». В нашем примере матрица и так уже отсортирована как надо.
Затем для каждой строки (n) матрицы находим коэффициент путем деления последующих элементов столбца (n) на главный элемент (тот, что на диагонали).
На полученный коэффициент умножаем всю строку (n) и вычитаем ее из всех последующих строк матрицы.
Получим матрицу такого треугольного вида:
| А | Б | В | Г | Свободный член |
| -120 | 0 | 0 | 20 | -1600 |
| 0 | -170 | 0 | 3,3333 | -2566,67 |
| 0 | 0 | -160 | 0,78 | -3203,92 |
| 0 | 0 | 0 | -139,75 | -4101,23 |
Далее будем вычислять значение неизвестных, начиная с самой нижней строки:
Г) Г = -4101,23 / -139,75 = 29,3458435637;
В) В = (-3203,92 — 0,78*29,3458435637) / -160 = 20,1683619783;
Б) Б = (-2566,67 – 3,33*29,3458435637– 0 * 20,1683619783) / -170 = 15,6734479130;
А) А = (-1600 – 20 * 29,3458435637–0 * 20,1683619783- 0 * 15,6734479130) / -120 = 18,2243072606;
Функция РешитьМетодомГауса ( Матрица )
Если Матрица = Неопределено Тогда
Возврат Неопределено ;
КонецЕсли ;
КоличествоСтолбцов = Матрица [ 0 ] .Количество ();
МассивКоэффициентов = Новый Массив ( КоличествоСтрок );
Для Стр = 0 По КоличествоСтрок — 2 Цикл
//Поиск максимального элемента в столбце
МаксимальныйЭлементСтолбца = Матрица [ Стр][Стр] ;
Для ПодСтр = Стр По КоличествоСтрок — 1 Цикл
Если МодульЧисла ( Матрица [ ПодСтр ][ Стр ] ) > МодульЧисла ( МаксимальныйЭлементСтолбца ) Тогда
МаксимальныйЭлементСтолбца = Матрица [ ПодСтр ][ Стр] ;
КонецЕсли ;
КонецЦикла ;
//Система не разрешима если максимальный элемент равен нулю
Если МаксимальныйЭлементСтолбца = 0 Тогда
Возврат Неопределено ;
КонецЕсли ;
//Меняем текущую строку со строкой с максимальным элементом
Если НомерСтрокиМаксЭлемента Стр Тогда
Для Стб = 0 По КоличествоСтолбцов — 1 Цикл
Матрица [ Стр ][ Стб ] = Матрица [ НомерСтрокиМаксЭлемента ][ Стб ] ;
Матрица [ НомерСтрокиМаксЭлемента ][ Стб ] = Буфер ;
КонецЦикла ;
КонецЕсли ;
//Вычисляем коэффициенты для каждой строки
Для ПодСтр = 0 По КоличествоСтрок — 2 — Стр Цикл
МассивКоэффициентов [ Стр + 1 + ПодСтр ] = Матрица [ Стр + 1 + ПодСтр ][ Стр ]/ Матрица [ Стр ][ Стр ] ;
КонецЦикла ;
Для ПодСтр = Стр + 1 По КоличествоСтрок — 1 Цикл
Для Стб = Стр По КоличествоСтолбцов — 1 Цикл
Матрица [ ПодСтр ][ Стб ] = Матрица [ ПодСтр ][ Стб ] – МассивКоэффициентов [ ПодСтр ] * Матрица [ Стр ][ Стб ] ;
КонецЦикла ;
КонецЦикла ;
КонецЦикла ;
//Вычисление корней СЛАУ обратным ходом
Решение = Новый Массив ( КоличествоСтрок );
Для Стр = — КоличествоСтрок + 1 По 0 Цикл
Если Стр = — КоличествоСтрок + 1 Тогда // первый виток
Решение [ — Стр ] = Матрица [ — Стр ][ КоличествоСтолбцов — 1 ]/ Матрица [ — Стр ][ — Стр ] ;
Иначе
Для ПодСтр = — Стр + 1 По КоличествоСтрок — 1 Цикл
Матрица [ — Стр ][ КоличествоСтолбцов — 1 ] = Матрица [ — Стр ][ КоличествоСтолбцов — 1 ] — Решение [ ПодСтр ] * Матрица [ — Стр ][ ПодСтр ] ;
КонецЦикла ;
Решение[ — Стр] = Матрица[ — Стр][КоличествоСтолбцов — 1]/Матрица[ — Стр][ — Стр] ;
КонецЕсли ;
КонецЦикла ;
Возврат Решение ;
КонецФункции
Функция МодульЧисла ( Число )
Возврат ? ( Число > 0, Число, — Число );
Метод простых итераций
Приводим матрицу к диагональному виду, как и в методе Гаусса. В нашем примере матрица и так уже отсортирована как надо.
| А | Б | В | Г | Свободный член |
| -120 | 0 | 0 | 20 | -1600 |
| 20 | -170 | 0 | 0 | -2300 |
| 0 | 40 | -160 | 0 | -2600 |
| 0 | 0 | 50 | -140 | -3100 |
Для каждой строки матрицы элемент Хnна диагонали меняем местами со свободным членом, меняя и знак.
Уравнения будут выглядеть так:
А) 1600 + 0 * Б + 0 * В + 20 * Г = 120 * А
Б) 20 * А + 2300 + 0 * В + 0 * Г = 170 * Б
В) 0 * А + 40 * Б + 2600 — 105 * Г = 55 * В
Г) 0 * А + 0 * Б + 50 * В + 3100 = 140 * Г
.. и разделим каждое уравнение на коэффициент в правой части уравнений:
А) 13,33 + 0 *Б + 0 * В + 0,17 * Г = А
Б) 0,12 *А + 13,53 + 0 * В + 0 * Г = Б
В) 0 * А + 0,73 * Б + 47,27 — 1,91 * Г = В
Г) 0 * А + 0 * Б + 0,36 * В + 22,14 = Г
Проще говоря, мы разрешили каждое уравнение (n) относительно Хn.
Матрица примет вид:
| А | Б | В | Г | Свободный член |
| 13,333333333 | 0 | 0 | 0,166666667 | 1 |
| 0,117647059 | 13,529411765 | 0 | 0 | 1 |
| 0 | 0,727272727 | 47,272727273 | -1,909090909 | 1 |
| 0 | 0 | 0,357142857 | 22,142857143 | 1 |
Затем весь процесс выглядит так:
О итерация — Подставляем в каждое уравнение значение неизвестных (А,Б,В,Г) равными 0, получаем первое решение
1 итерация – подставляем в каждое уравнение значение неизвестных (А,Б,В,Г), рассчитанные на предыдущей итерации
— рассчитываем погрешности для каждого неизвестного вычитанием текущего решения из предыдущего.
— сравниваем максимальное значение погрешности с заданной точностью. Если погрешность меньше, тогда решение найдено.
И так далее, пока не будет найдено решение.
Опытным путем была подобрана точность решения, равная 0,0000001, при которой решение методом итераций дает результат вычисления сильно приближенный к решению методом Гаусса.
Результат метода итераций такой:
Код метода такой:
Функция РешитьМетодомИтераций ( Матрица )
Если Матрица = Неопределено Тогда
Если Точность = 0 Тогда
Сообщить ( «Не указана точность вычислений.» );
КоличествоСтолбцов = Матрица [ 0 ] .Количество ();
Решение = Новый Массив ( КоличествоСтрок );
// отсортируем матрицу так, чтобы по диагонали располагались наибольшие по модулю значения
Для Стр = 0 По КоличествоСтрок — 1 Цикл
//Поиск максимального элемента в столбце
МаксимальныйЭлементСтолбца = Матрица [ Стр ][ Стр ];
Для ПодСтр = Стр По КоличествоСтрок — 1 Цикл
Если МодульЧисла ( Матрица [ ПодСтр ][ Стр ]) > МодульЧисла ( МаксимальныйЭлементСтолбца ) Тогда
МаксимальныйЭлементСтолбца = Матрица [ ПодСтр ][ Стр ];
//Система не разрешима если максимальный элемент равен нулю
Если МаксимальныйЭлементСтолбца = 0 Тогда
//Меняем текущую строку со строкой с максимальным элементом
Если НомерСтрокиМаксЭлемента Стр Тогда
Для Стб = 0 По КоличествоСтолбцов — 1 Цикл
Буфер = Матрица [ Стр ][ Стб ];
Матрица [ Стр ][ Стб ] = Матрица [ НомерСтрокиМаксЭлемента ][ Стб ];
Матрица [ НомерСтрокиМаксЭлемента ][ Стб ] = Буфер ;
// например, матрица стала такой:
// x1 x2 x3 x4 Св Чл
// -120 0 0 20 -1600 // уравнение для х1
// 20 -170 0 0 -2300 // уравнение для х2
// 0 40 -160 0 -2600 // уравнение для х3
// 0 0 50 -140 -3100 // уравнение для х4
//Разрешим каждое уравнение относительно Хn
Для Стр = 0 по КоличествоСтрок — 1 Цикл
// Меняем местами коэффициент аргумента Хn и свободный член, одновременно меняя знак.
// Как при перестановке члена уравнения за знак «=»
Буфер = — Матрица [ Стр ][ Стр ];
Матрица [ Стр ][ Стр ] = — Матрица [ Стр ][ КоличествоСтолбцов — 1 ];
Матрица [ Стр ][ КоличествоСтолбцов — 1 ] = Буфер ;
// разделим строку на коэффициент аргумента Хn, т.е на значение в буфере
Для Кол = 0 по КоличествоСтолбцов — 1 Цикл
Матрица [ Стр ][ Кол ] = Матрица [ Стр ][ Кол ] / Буфер ;
// Матрица из примера примет вид:
// x1 x2 x3 x4 Св Чл
// 13,333 0 0 0,167 1 // уравнение для х1
// 0,118 13,529 0 0 1 // уравнение для х2
// 0 0,727 47,273 -1,909 1 // уравнение для х3
// 0 0 0,357 22,143 1 // уравнение для х4
/ колонки: от 0 до КоличествоСтрок матрицы — для значений вычисленных Х
// колонки: + КоличествоСтрок матрицы — для значений погрешностей П
// еще одна колонка для мычисления максимального значения погрешности в строке
МассивРешений = Новый Массив ();
// добавим нулевое решение
СтрокаРешения = Новый Массив ( КоличествоСтрок + КоличествоСтрок + 1 );
Для Инд = 0 по СтрокаРешения.ВГраница () Цикл
СтрокаРешения [ Инд ] = 0 ;
Пока не РешениеЕсть Цикл
ПредыдущееРешение = МассивРешений [ ВсегоРешений — 1 ];
// добавим новую строку решения
СтрокаРешения = Новый Массив ( КоличествоСтрок + КоличествоСтрок + 1 );
Для Инд = 0 по КоличествоСтолбцов — 2 Цикл
// найдем уравнение матрицы, соответствующее решаемому аргументу Х
УравнениеМатрицы = Матрица [ Инд ];
//Обойдем все колонки уравнения и сложим, перемножив на значения Х из предыдущего решения
Для Кол = 0 по КоличествоСтолбцов — 2 Цикл
Если Кол = Инд Тогда
РешениеХ = РешениеХ + УравнениеМатрицы [ Кол ];
РешениеХ = РешениеХ + УравнениеМатрицы [ Кол ] * ПредыдущееРешение [ Кол ];
СтрокаРешения [ Инд ] = РешениеХ ;
ИндПогрешности = КоличествоСтолбцов — 1 + Инд ;
СтрокаРешения [ ИндПогрешности ] = РешениеХ — ПредыдущееРешение [ Инд ];
СтрокаПогрещностей = СтрокаПогрещностей + Строка (Формат( СтрокаРешения [ ИндПогрешности ], «ЧРД=.; ЧГ=0» )) + «,» ;
// добавим решение в массив решений
ВсегоРешений = ВсегоРешений + 1 ;
// определим, найдено ли решение
СтрокаПогрещностей = СтрокаПогрещностей + «0» ;
Выполнить ( «ПогрешностьРешения = Макс(» + СтрокаПогрещностей + «);» );
Если ПогрешностьРешения = 0 Тогда
СтрокаРешения [ КоличествоСтрок + КоличествоСтрок ] = ПогрешностьРешения ;
РешениеЕсть = ПогрешностьРешения Точность ;
КоличествоИтераций = ВсегоРешений — 1 ; // исключили нулевое решение
Для Стр = 0 по КоличествоСтолбцов — 2 Цикл
Решение [ Стр ] = СтрокаРешения [ Стр ];
Сравним решения СЛАУ
| Склад | Метод Гаусса | Метод простых итераций |
| А | 18,2243072606 | 18,2243072542 |
| Б | 15,6734479130 | 15,6734479099 |
| В | 20,1683619783 | 20,1683619754 |
| Г | 29,3458435637 | 29,3458435562 |
Как видно из результатов вычислений разными методами, решения расходятся, начиная с 7 знака после запятой. В контексте решаемой задачи 6 знаков после запятой будет более чем достаточно.
4. Подставляем в таблицу движений полученные значения.
На последнем шаге решения задачи умножим количества операций на рассчитанные «суммы ТР на единицу» и получим сумму движений.
| № | Период | Операция | Склад | Корр склад | Количество приход | Количество расход | Сумма ТР приход | Сумма ТР расход |
| 1 | 01.07.2014 | Сальдо | А | 100 | 1000 | |||
| 2 | 01.07.2014 | Сальдо | Б | 150 | 1500 | |||
| 3 | 01.07.2014 | Сальдо | В | 120 | 1600 | |||
| 4 | 01.07.2014 | Сальдо | Г | 90 | 1900 | |||
| 5 | 05.07.2014 | Перемещение | Б | А | 20 | 1164,49 | ||
| 6 | 05.07.2014 | Перемещение | А | 20 | 364,49 | |||
| 7 | 10.07.2014 | Перемещение | В | Б | 40 | 1626,94 | ||
| 8 | 10.07.2014 | Перемещение | Б | 40 | 626,94 | |||
| 9 | 11.07.2014 | Комплектация | Г | 60 | 1760,75 | |||
| 10 | 12.07.2014 | Перемещение | Г | В | 50 | 2208,42 | ||
| 11 | 12.07.2014 | Перемещение | В | 50 | 1008,42 | |||
| 12 | 13.07.2014 | Комплектация | Г | 40 | 1173,83 | |||
| 13 | 16.07.2014 | Перемещение | А | Г | 20 | 1186,92 | ||
| 14 | 16.07.2014 | Перемещение | Г | 20 | 586,92 | |||
| 15 | 17.07.2014 | Переработка | В | 15 | 302,53 | |||
| 16 | 18.07.2014 | Переработка | В | 20 | 403,37 | |||
| 17 | 20.07.2014 | Реализация | А | 100 | 1822,43 | |||
| 18 | 25.07.2014 | Реализация | Б | 130 | 2037,55 | |||
| 19 | 31.07.2014 | Сальдо | А | 0 | 0 | |||
| 20 | 31.07.2014 | Сальдо | Б | 0 | 0 | |||
| 21 | 31.07.2014 | Сальдо | В | 105 | 2117,68 | |||
| 22 | 31.07.2014 | Сальдо | Г | 140 | 4108,42 |
Во вложении обработка, в которой я реализовал сравнение двух методов решения СЛАУ на примере массива 4 х 5
Sitkovskiy Konstantin — за функцию решения СЛАУ по методу Гаусса
📺 Видео
6 способов в одном видеоСкачать

Матричный метод решения систем уравненийСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Учет себестоимости 1C:ERP. Устройство и принципы работы.Скачать