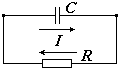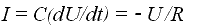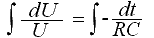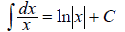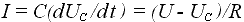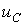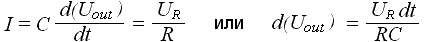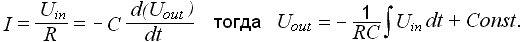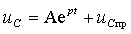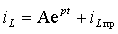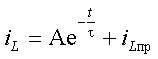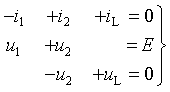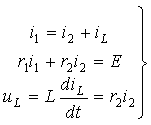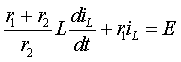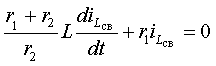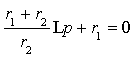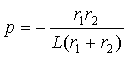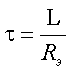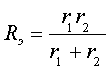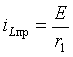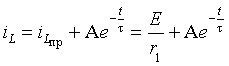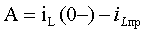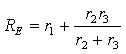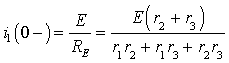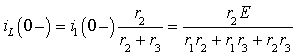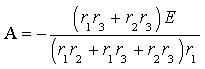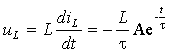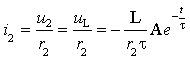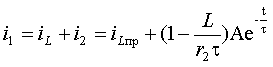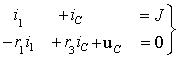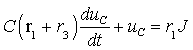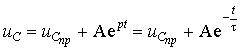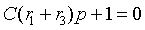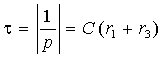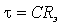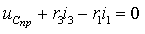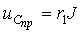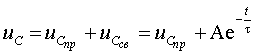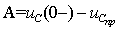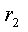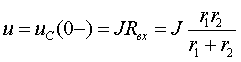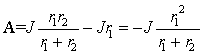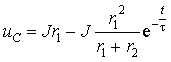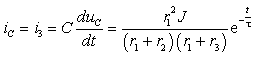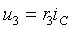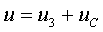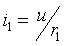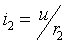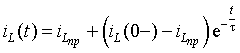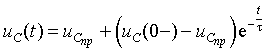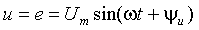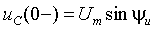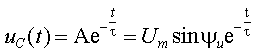Расчет rc цепи дифференциальное уравнение

Активные на ОУ и пассивные RC и RL дифференцирующие и интегрирующие цепи: схемы, осциллограммы и онлайн калькулятор расчёта постоянной времени цепи.

Святая простота! Что может быть проще?
А проще могут быть лишь чётко сформулированные определения дифференцирующей и интегрирующей цепей, не обременённые ни лингвистическими излишествами, ни всякого рода необязательными формулами.

Итак, полностью оправдывая свои названия:
Дифференцирующая цепь — это цепь, в которой мгновенное значение напряжения на выходе прямо
пропорционально дифференциалу входного напряжения;
Интегрирующая цепь — цепь, у которой мгновенное значение выходного напряжения не менее прямо
пропорционально интегралу входного напряжения.

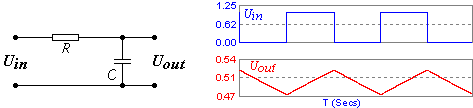
Начнём с RC и RL дифференцирующих цепей.

Эти цепи решают две основные задачи преобразования сигналов:
1. Формирование импульсов малой длительности (укорочение входных импульсов), которые далее используются для запуска триггеров, одновибраторов и других устройств,
2. Выполнение математической операции дифференцирования (получение производной по времени) для устройств вычислительной техники, аппаратуры авторегулирования и т.д.

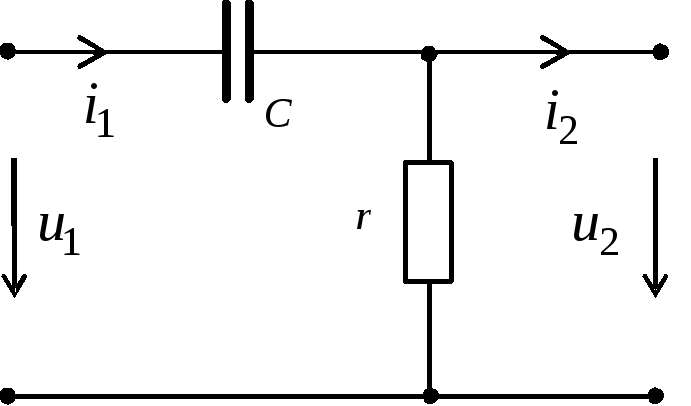
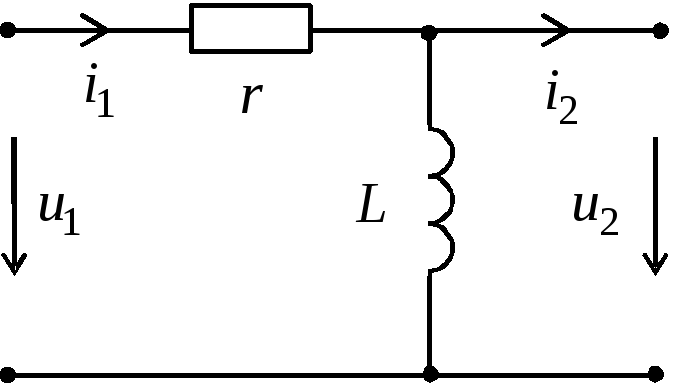
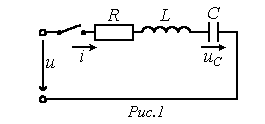
Рис.1.

Основной характеристикой данных цепей является постоянная времени цепи τ = rC, либо τ = L/r.
В общем случае сигнал на выходе цепи описывается следующей формулой:
U₂ = τ ×d(U₁-U₂)/dt.
Однако на практике, если мы выбираем τ τ ×dU₁/dt.

Приведём несколько поясняющих картинок.

На Рис.2 приведены осциллограммы напряжений на выходах дифференцирующих цепей, в зависимости от различных соотношений постоянной времени цепи τ и длительности входного импульса tи.

В начальный момент подачи входного импульса, напряжение на выходе U_вых практически моментально достигает амплитудного значения входного U_вх, а затем идёт относительно плавный спад до:
U_вх/√e ≈ 0,61Uвх за время, равное τ /2,
U_вх/e ≈ 0,37Uвх за время, равное τ ,
U_вх/e 2 ≈ 0,135Uвх за время, равное 2 τ ,
U_вх/e 3 ≈ 0,05Uвх за время, равное 3 τ ,
где e — это основание натурального логарифма ≈ 2,72.

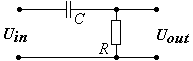
Переходим к интегрирующим RC и RL цепям.

Интегрирующая цепь предназначена для формирования импульсов большой длительности, т. е. для удлинения или расширения импульсов, преобразования импульсов по интегральному закону, получения линейно изменяющегося напряжения. Отсюда и другое название интегрирующей цепи — удлиняющая цепь.

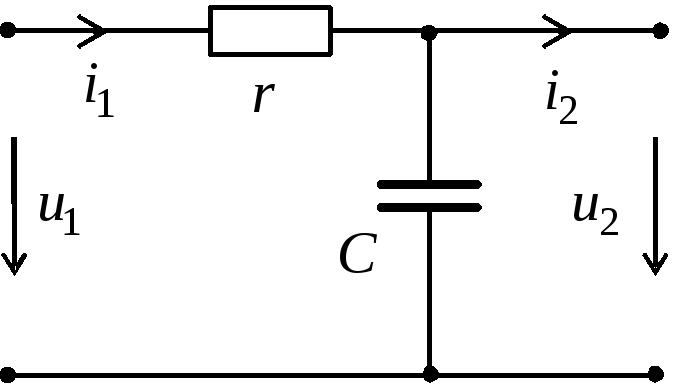
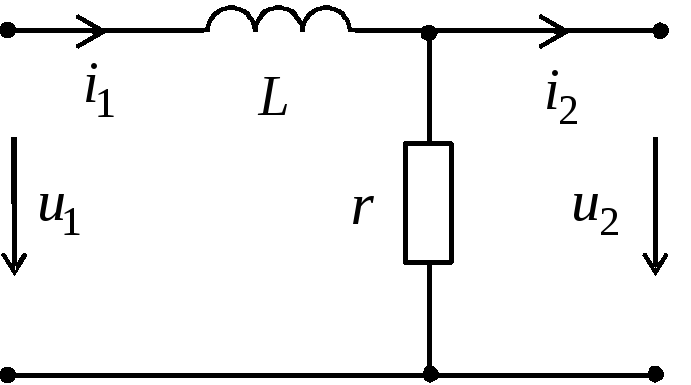
Рис.3.

Значение величины постоянной времени интегрирующей цепи ничем не отличается от дифференцирующих собратьев: τ = rC, либо τ = L/r.

Для корректного выполнения цепью интегрирующих функций должно выполняться условие:
τ >> T_и, где T_и — длительность входного импульса. При соблюдении этого условия выходное напряжение U₂ описывается следующей формулой: U₂ = 1/ τ ×∫U₁dt.

Продолжим уроки рисования.

На Рис.4 приведены осциллограммы напряжений на выходах интегрирующих цепей, в зависимости от различных соотношений постоянной времени цепи τ и длительности входного импульса tи.

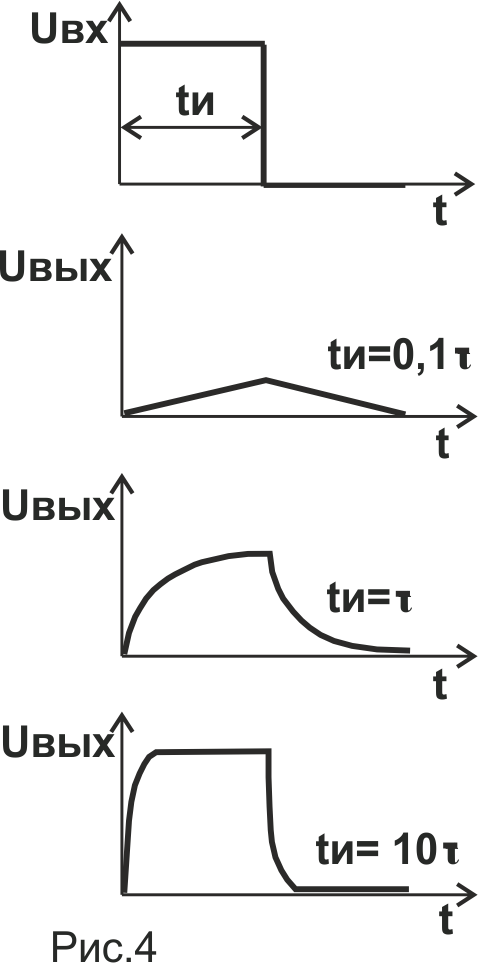
В начальный момент подачи входного импульса, напряжение на выходе U_вых равно 0, после чего начинает расти со скоростью, обратно пропорциональной значению τ и достигает следующих значений:
U_вх×(1-1/√e) ≈ 0,39Uвх за время, равное τ /2,
U_вх×(1-1/e) ≈ 0,63Uвх за время, равное τ ,
U_вх×(1-1/e 2 ) ≈ 0,86Uвх за время, равное 2 τ ,
U_вх×(1-1/e 3 ) ≈ 0,95Uвх за время, равное 3 τ ,
где e — это по-прежнему основание всё того же пресловутого натурального логарифма ≈ 2,72.

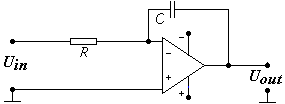
Снять ограничения по выбору постоянной времени дифференцирующих и интегрирующих цепей (по отношению к длительности входного импульса) можно посредством применения операционных усилителей (Рис.5).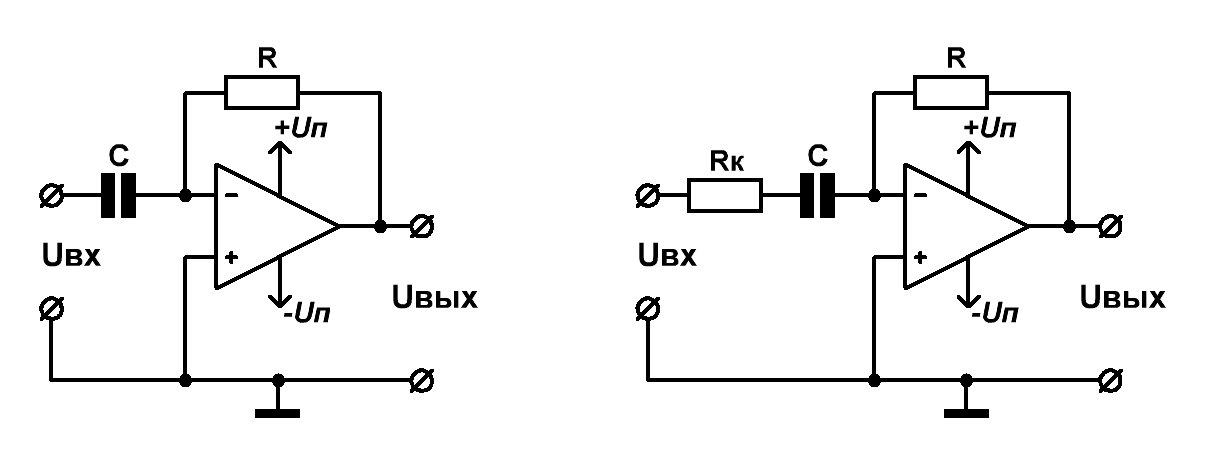

Рис.5 Схемы активных дифференциаторов на ОУ

Здесь всё по аналогии с пассивными цепями, только без ограничений по длительности входного импульса и, поскольку включение операционного усилителя инвертирующее – со знаком минус:
U_вых = – RC×dU_вх/dt.
Уменьшение реактивного сопротивления конденсатора С при росте частоты приводит к синхронному повышению коэффициента усиления активного дифференциатора, что создаёт условия для возможного самовозбуждения устройства. Для того, чтобы этого избежать в схему активного дифференциатора часто вводят корректирующее сопротивление Rк (Рис.5 справа). Применение данного резистора ограничивает коэффициент усиления на BЧ, что, в свою очередь, обеспечивает более высокую динамическую устойчивость.
Для того чтобы не сильно пострадала точность преобразования, номинал корректирующего резистора Rк следует выбрать небольшим, как минимум в 100 раз меньшим, чем величина сопротивления резистора R.

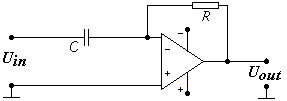
Переходим к схемам интеграторов, построенных на операционных усилителях (Рис.6).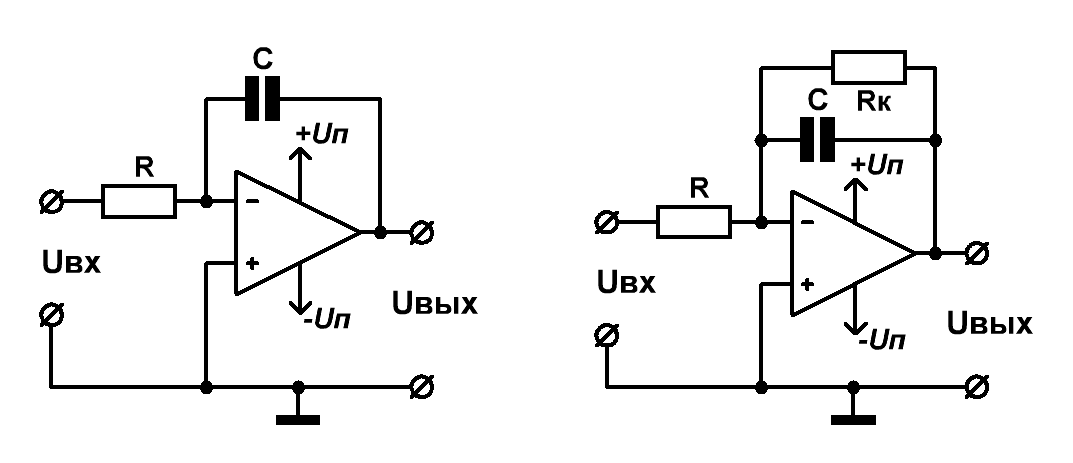

Рис.6 Схемы активных интеграторов на ОУ

Здесь тоже всё без изменений: U_вых = – ∫U_вхdt / (RC).

В отличие от дифференциатора, схема интегрирующего усилителя имеет высокую устойчивость, но за счёт отсутствия обратной связи по постоянному току, имеет склонность к дрейфу выходного напряжения. Связано это с ненулевым значением параметра смещения выходного уровня реального ОУ.
Ошибку напряжения сдвига можно уменьшить посредством включения параллельно конденсатору С корректирующего резистора Rк (Рис.6 справа), образующего совместно с входным резистором R ООС по постоянному току. Для сохранения точности преобразования номинал Rк как минимум в 100 раз должен превышать сопротивление резистора R.

Ну и под занавес приведём таблицу для расчёта значения величины постоянной времени дифференцирующих и интегрирующих цепей τ .
Как уже говорилось — это величина одинакова для обоих типов цепей и равна τ = rC, либо τ = L/r.
Незадействованные элементы при вводе данных можно оставить без внимания.

Видео:Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Дифференцирующая цепь RC

Постоянная времени цепи RC

Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе, согласно закону Ома, составит U/R, где U — напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

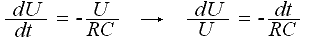
Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = — t/RC + Const.
Выразим из него напряжение U потенцированием: U = e -t/RC * e Const .
Решение примет вид:

Здесь Const — константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону e -t/RC .

Экспонента — функция exp(x) = e x
e – Математическая константа, приблизительно равная 2.718281828.

Постоянная времени τ

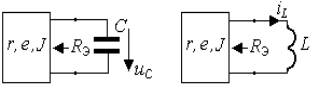
Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U, в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

При t = RC, напряжение на конденсаторе составит U_C = U(1 — e -1 ) = U(1 — 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 — 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 — 1/e 3 )*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 — 1/e 5 )*100% ≈ 99% значения U.

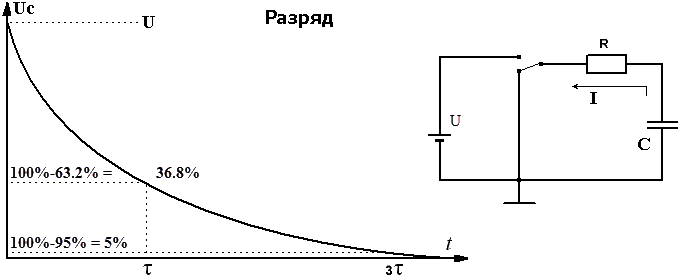
Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R, тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue -t/τ = U/e t/τ .

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.
За время 3τ конденсатор разрядится до (1/e 3 )*100% ≈ 5% от значения U.
За время 5τ до (1/e 5 )*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

Связь мгновенных значений напряжений и токов на элементах

Электрической цепи

Резистор (идеальное активное сопротивление)	Катушка индуктивности (идеальная индуктивность)	Конденсатор (идеальная емкость)
	;	;

Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (см. рис. 1) можно записать

.

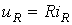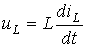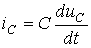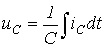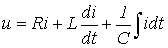(1)

Подставив в (1) значение тока через конденсатор

,

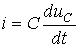
получим линейное дифференциальное уравнение второго порядка относительно

.

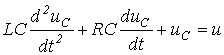
В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии,имеет вид:

,

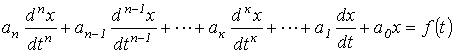(2)

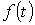
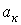
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); — известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); — к-й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.

В общем случае порядок дифференциального уравнения определяется соотношением

,

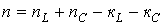(3)

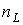
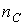
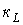
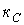
где и — соответственно число катушек индуктивности и конденсаторов после указанного упрощения исходной схемы; — число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки); — число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение 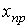, соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для ).

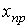
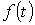
Частное решение уравнения (2) определяется видом функции , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета стационарного режима работы схемы после коммутации любым из рассмотренных ранее методов расчета линейных электрических цепей.

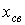
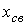
Вторая составляющая общего решения х уравнения (2) – решение (2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная — свободной составляющей.

В соответствии с вышесказанным, . общее решение уравнения (2) имеет вид

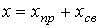(4)

Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.

Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.

Начальные условия. Законы коммутации

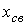
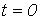
В соответствии с определением свободной составляющей в ее выражении имеют место постоянные интегрирования , число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени (момент коммутации). Независимые начальные условия определяются на основании законов коммутации (см. табл. 2).

Таблица 2. Законы коммутации

Название закона	Формулировка закона
Первый закон коммутации (закон сохранения потокосцепления)	Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .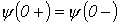
Второй закон коммутации (закон сохранения заряда)	Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: .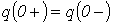

— See more at: http://www.toehelp.ru/theory/toe/lecture24/lecture24.html#sthash.jqyFZ18C.dpuf

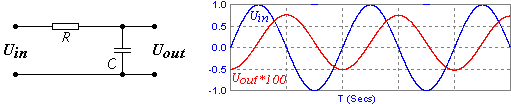
Интегрирующая цепь RC

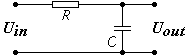
Рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C, представленную на рисунке.

Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора dQ/dt = C(dU/dt) и закона Ома U/R. Напряжение на выводах резистора обозначим U_R.
Тогда будет иметь место равенство:

Проинтегрируем последнее выражение 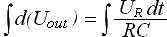. Интеграл левой части уравнения будет равен U_out + Const . Перенесём постоянную составляющую Const в правую часть с тем же знаком.
В правой части постоянную времени RC вынесем за знак интеграла:

В итоге получилось, что выходное напряжение U_out прямо-пропорционально интегралу напряжения на выводах резистора, следовательно, и входному току I_in.
Постоянная составляющая Const не зависит от номиналов элементов цепи.

Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения U_out от интеграла входного U_in, необходима пропорциональность входного напряжения от входного тока.

Нелинейное соотношение U_in/I_in во входной цепи вызвано тем, что заряд и разряд конденсатора происходит по экспоненте e -t/τ , которая наиболее нелинейна при t/τ ≥ 1, то есть, когда значение t соизмеримо или больше τ.
Здесь t — время заряда или разряда конденсатора в пределах периода.
τ = RC — постоянная времени — произведение величин R и C.
Если взять номиналы RC цепи, когда τ будет значительно больше t, тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током.

Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость U_in/I_in ≈ R.
В таком случае выходное напряжение U_out будет с допустимой погрешностью пропорционально интегралу входного U_in.
Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.

В большинстве случаев, переменная составляющая интеграла не требуется при использовании таких цепей, нужна только постоянная Const, тогда номиналы RC можно выбирать по возможности большими, но с учётом входного сопротивления следующего каскада.

В качестве примера, сигнал с генератора — положительный меандр 1V периодом 2 mS подадим на вход простой интегрирующей цепи RC с номиналами:
R = 10 kOhm, С = 1 uF. Тогда τ = RC = 10 mS.

В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.
График показывает, что выходное напряжение на уровне постоянной составляющей 0.5в будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её a), а интеграл константы будет линейной функцией. ∫adx = ax + Const. Величина константы a определит тангенса угла наклона линейной функции.

Проинтегрируем синусоиду, получим косинус с обратным знаком ∫sinxdx = -cosx + Const.
В данном случае постоянная составляющая Const = 0.

Если подать на вход сигнал треугольной формы, на выходе будет синусоидальное напряжение.
Интеграл линейного участка функции — парабола. В простейшем варианте ∫xdx = x 2 /2 + Const.
Знак множителя определит направление параболы.

Недостаток простейшей цепочки в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.

Рассмотрим в качестве интегратора Операционный Усилитель (ОУ) по схеме, показанной на рисунке.

С учётом бесконечно большого сопротивления ОУ и правила Кирхгофа здесь будет справедливо равенство:

Напряжение на входах идеального ОУ здесь равно нулю, тогда на выводах конденсатора U_C = U_out = — U_in .
Следовательно, U_out определится, исходя из тока общей цепи.

При номиналах элементов RC, когда τ = 1 Sec, выходное переменное напряжение будет равно по значению интегралу входного. Но, противоположно по знаку. Идеальный интегратор-инвертор при идеальных элементах схемы.

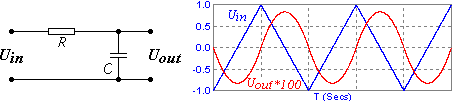
Дифференцирующая цепь RC

Рассмотрим дифференциатор с применением Операционного Усилителя.

Идеальный ОУ здесь обеспечит равенство токов I_R = — I_C по правилу Кирхгофа.
Напряжение на входах ОУ равно нулю, следовательно, выходное напряжение U_out = U_R = — U_in = — U_C .
Исходя из производной заряда конденсатора, закона Ома и равенства значений токов в конденсаторе и резисторе, запишем выражение:

Отсюда видим, что выходное напряжение U_out пропорционально производной заряда конденсатора dU_in /dt , как скорости изменения входного напряжения.

При величине постоянной времени RC, равной единице, выходное напряжение будет равно по значению производной входного напряжения, но противоположно по знаку. Следовательно, рассмотренная схема дифференцирует и инвертирует входной сигнал.

Производная константы равна нулю, поэтому постоянная составляющая при дифференцировании на выходе будет отсутствовать.

В качестве примера, подадим на вход дифференциатора сигнал треугольной формы. На выходе получим прямоугольный сигнал.
Производная линейного участка функции будет константой, знак и величина которой определится наклоном линейной функции.

Для простейшей дифференцирующей цепочки RC из двух элементов используем пропорциональную зависимость выходного напряжения от производной напряжения на выводах конденсатора.

Если взять номиналы элементов RC, чтобы постоянная времени была на 1-2 порядка меньше длины периода, тогда отношение приращения входного напряжения к приращению времени в пределах периода может определять скорость изменения входного напряжения в определённой степени точно. В идеале это приращение должно стремиться к нулю. В таком случае основная часть входного напряжения будет падать на выводах конденсатора, а выходное будет составлять незначительную часть от входного, поэтому для вычислений производной такие схемы практически не используются.

Наиболее часто дифференцирующие и интегрирующие цепи RC применяют для изменения длины импульса в логических и цифровых устройствах.
В таких случаях номиналы RC рассчитывают по экспоненте e -t/RC исходя из длины импульса в периоде и требуемых изменений.
Например, ниже на рисунке показано, что длина импульса T_i на выходе интегрирующей цепочки увеличится на время 3τ. Это время разряда конденсатора до 5% амплитудного значения.

На выходе дифференцирующей цепи амплитудное напряжение после подачи импульса появляется мгновенно, так как на выводах разряженного конденсатора оно равно нулю.
Далее следует процесс заряда и напряжение на выводах резистора убывает. За время 3τ оно уменьшится до 5% амплитудного значения.

Здесь 5% — величина показательная. В практических расчётах этот порог определится входными параметрами применяемых логических элементов.

Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Расчет rc цепи дифференциальное уравнение

3.2 Электрические цепи первого порядка

Порядок электрической цепи определяется числом реактивных элементов. Цепь первого порядка ( n = 1) включает один реактивный элемент — индуктивность или емкость и любое число резистивных элементов и независимых источников питания. По отношению к реактивному элементу всю остальную цепь можно считать резистивным активным двухполюсником (рис. 3.1а,б).

Рис. 3.1. Схематичное изображение цепи первого порядка:

а) RC -цепь; б) RL -цепь

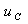
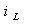
Переходный процесс в такой цепи описывается дифференциальным уравнением первого порядка, решение которого для переменных состояния или будет иметь вид

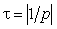
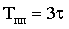
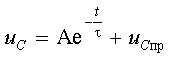
где p — корень характеристического уравнения. Эта величина вещественна и отрицательна, она выполняет роль коэффициента затухания. Обратное отношение , измеряемое в секундах, определяет скорость переходного процесса и называется постоянной времени. Принято считать длительностью переходного процесса величину равную . C учетом этого определения решение чаще всего записывают в виде

или

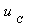
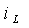
Итак, для того чтобы получить решение для переменных состояния или , достаточно в выражениях (3.10) найти три значения:

1. Постоянную времени τ для свободной составляющей режима;

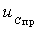
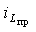
2. Принужденную составляющую — или ;

3. Постоянную интегрирования A.

Рассмотрим эту триединую задачу на примерах.

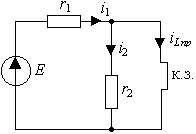
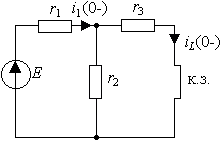
Пример 3.1. В цепи рис. 3.2а, которая питается от источника постоянного напряжения E , происходит замыкание ключа S. Найти закон изменения тока в индуктивности.

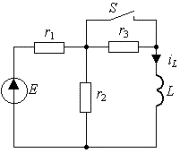
Рис. 3.2. Схема RL -цепи первого порядка:

а) исходная цепь( t б) схема после коммутации( t >0)

Предварительный анализ цепи показывает, что в процессе коммутации сопротивление замыкается накоротко и не участвует в переходном процессе, а сам процесс развивается за счет внешнего источника энергии E и энергии магнитного поля, запасенной в индуктивности к моменту коммутации. На рис.3.2б представлена измененная схема цепи после замыкания ключа.

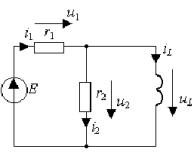
В соответствии с требованием классического метода для времени t>0 составим систему уравнений по законам Кирхгофа [1]

После подстановки компонентных соотношений, связывающих токи и напряжения в отдельных элементах цепи, получим

Подставим первое и третье уравнение во второе, чем сведем систему

к одному уравнению относительно переменной состояния :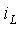

Уравнение для свободной составляющей режима получим, приравняв правую часть к нулю

Переход к характеристическому уравнению произведем заменой d/dt на p, а 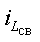на 1 :

Найдем корень характеристического уравнения, модуль которого совпадает с коэффициентом затухания

Постоянную времени получим как величину обратную коэффициенту затухания

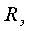
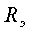
Анализ выражений (3.11) и (3.12) показывает, что постоянная времени, пропорциональна величине индуктивности L и обратно пропорциональна некоторому эквивалентному резистивному сопротивлению . Величина совпадает с входным сопротивлением исследуемой цепи, измеряемым или вычисляемым со стороны реактивного элемента [1].Этот вывод распространяется на любую цепь первого порядка, содержащую одну индуктивность и неограниченное число резистивных элементов и источников энергии. Таким образом, для получения конечного выражения (3.11) не обязательно составлять и решать систему алгебраических и дифференциальных уравнений. Достаточно найти входное сопротивление цепи со стороны реактивного элемента, а затем воспользоваться формулой (3.11).

Входное сопротивление цепи определяется в три этапа:

а. Изображается схема цепи после коммутации ( t>0);

б. В этой цепи вместо реактивного элемента рисуют разомкнутые зажимы, по отношению к которым в дальнейшем определяют входное сопротивление. Далее исключают все источники энергии: источники напряжения замыкают накоротко, а источники тока разрывают;

в. Последовательно упрощают цепь, объединяя последовательно и параллельно соединенные резистивные элементы, чем сводят цепь к эквивалентному сопротивлению, которое и будет искомым входным .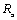

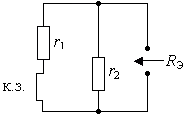
Рис. 3.3. Схема для определения Рис. 3.4. Схема для определения

входного сопротивления активного принужденной составляющей

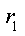
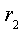
Для рассматриваемой цепи такая преобразованная схема показана на рис.3.3. Здесь вместо индуктивности изображены разомкнутые зажимы, со стороны которых требуется определить входное сопротивление, а вместо источника напряжения E показана короткозамкнутая перемычка. Сопротивления и , участвующие в переходном процессе, оказываются соединенными параллельно, и их эквивалентная замена совпадает в выражением (3.12), что и подтверждает вышесказанное.

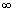
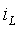
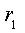
2. Принужденную составляющую решения определим для бесконечно большого момента времени ( t = ), когда переходный процесс закончен и цепь находится под воздействием стационарного постоянного источника питания E. Целесообразно для этого режима нарисовать расчетную схему. Если в цепи есть индуктивность, то она заменяется короткозамкнутой перемычкой, так как сопротивление индуктивности постоянному току равно нулю. Эта схема изображена на рис.3.4.Очевидно, что ток в индуктивности ограничен только сопротивлением :

Используя выражение (3.7), сформируем решение в виде суммы свободной и принужденной составляющей:

3. Постоянную интегрирования A определим на основании первого за-

кона коммутации (3.1).Для момента времени t = 0 имеем ,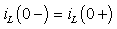

или .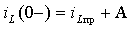

Отсюда следует общая формула определения постоянной интегрирования для цепей первого порядка, включающих одну индуктивность:

Для определения 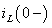нужно найти токи в цепи до коммутации ( t=0-). Исследуемая цепь представлена на рис. 3.5, в которой требуется определить ток i _L (0-). Снова решается задача расчета цепи постоянного тока, где индуктивность заменена короткозамкнутой перемычкой. Для решения могут быть использованы все методы расчета цепей постоянного тока, включая законы Кирхгофа и эквивалентные преобразования.

Рис. 3.5. Схема для анализа докоммутационного состояния цепи

Так как исследуемая цепь включает один источник энергии, то наиболее просто получить результат можно путем использования метода эквивалентных преобразований, вычисляя входное сопротивление цепи со стороны источника напряжения

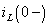
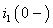
Искомый ток является частью тока и определяется правилом деления тока на части:

По формуле (3.13) окончательно определим постоянную интегрирования

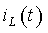
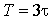
График функции тока схематично изображен на рис.3.6а. За время ток почти приближается к установившемуся значению, и это время считается длительностью переходного процесса.

Найденное выражение для переменной состояния 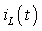позволяет определить все токи и напряжения. Для этого следует, опираясь на известную переменную состояния, решить обратную задачу: последовательно шаг за шагом, используя законы Ома и Кирхгофа, а также компонентные соотношения, определить токи и напряжения в других ветвях [1]. Для рассматриваемого примера найдем:

а. Напряжение на индуктивности:

Все найденные как следствие функции имеют разрыв в точке t = 0.

Рис. 3.6. Графики переходного процесса: а)ток в индуктивности; б)напряжение на индуктивности

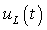
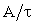
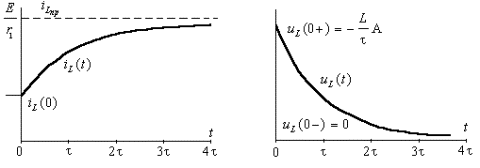
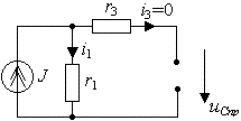
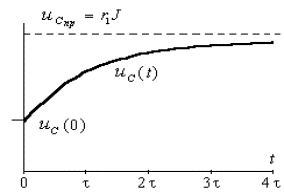
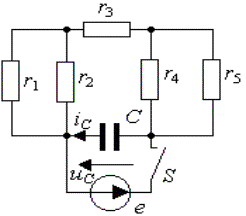
Например, график функции , изображенный на рис.3.6б, претерпевает скачок от нулевого значения до уровня — L (A — отрицательно), а затем плавно уменьшается до нулевого значения. Это означает, что, как правило, для функций, которые не являются переменными состояния, законы коммутации не выполняются, и, следовательно, определение для них постоянных интегрирования встречает дополнительные трудности. Если сразу искать выражения для этих функций, то требуется провести дополнительное исследование состояния цепи для момента времени t = 0+. Предложенный в этом пособии путь решения задачи через переменные состояния является наиболее оптимальным, так как требует знания только основных начальных условий, определяемых законами коммутации.

Пример 3.2. В цепи рис.3.7а найти закон изменения напряжения на емкости после размыкания ключа S, если цепь питается от источника постоянного тока J = const.

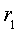
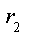
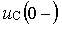
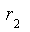
Предварительный анализ цепи показывает, что до размыкания ключа S ток источника протекал по параллельно соединенным сопротивлениям и , при этом емкость была заряжена до некоторого напряжения . После размыкания ключа сопротивление уже не участвует в переходном процессе, и структура цепи принимает вид рис.3.7б. В измененной цепи переходный процесс возникает за счет действия независимого источника энергии J и энергии, запасенной в емкости к моменту коммутации, в результате чего напряжение на емкости приходит к новому установившемуся состоянию.

Рис. 3.7. Схема RC -цепи первого порядка:

а) исходная цепь ( t б) схема после коммутации ( t >0)

1. Составим систему уравнений цепи по законам Кирхгофа:

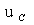
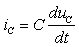
где переменной состояния для этой цепи будет напряжение . С учетом компонентного соотношения сведем систему уравнений к одному уравнению относительно переменной u _C

Как и следовало ожидать, переходный процесс описывается неоднородным дифференциальным уравнением первого порядка. Решение его имеет вид

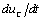
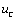
Приравнивая нулю правую часть уравнения и делая замену на p, а также на 1, получим характеристическое уравнение

откуда определяется единственный корень .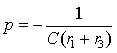

Постоянную времени цепи определим как модуль обратной величины от коэффициента затухания

Полученный результат, запишем в более общей форме

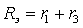
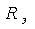
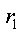
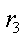
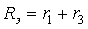
где ; т.е. постоянная времени для цепи первого порядка с одной емкостью вычисляется как произведение емкости С и некоторого эквивалентного сопротивления . Это эквивалентное сопротивление находится как входное сопротивление цепи со стороны реактивности (здесь емкости). На рис.3.8 показана эта схема, которая построена на основе исходной цепи рис.3.7б путем исключения источника энергии — заменой его на разомкнутые зажимы, а также обозначением разомкнутых зажимов вместо емкостного элемента. По отношению к обозначенным зажимам сопротивления и соединены последовательно, следовательно, , что совпадает с ранее полученным решением.

Второй способ определения быстрее приводит к поиску свободной составляющей режима, чем составление и решение системы уравнений.

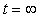
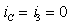
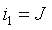
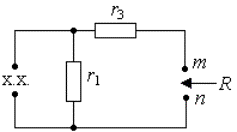
2. Принужденную составляющую режима определим для бесконечно большого момента времени , когда переходный процесс уже закончен, и цепь находится в новом энергетическом состоянии. Для этого момента времени схема цепи изображена на рис.3.9, где емкость С заменена разрывом ветви, поскольку сопротивление емкости постоянному току бесконечно большое. Следовательно, и , а из контура k имеем уравнение равновесия для напряжений:

Рис. 3.8. Схема для определения Рис. 3.9. Схема для анализа

входного сопротивления принужденных составляющих

активного двухполюсника режима

Объединяя свободную и принужденную составляющую режима, получим:

3. Постоянную интегрирования A для выражения (3.15) найдем на основе второго закона коммутации (3.4):

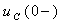
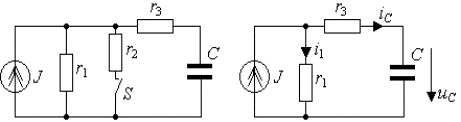
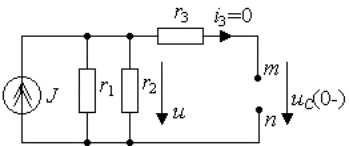
Формула (3.16) имеет общий характер и ей можно пользоваться для цепей первого порядка при наличии емкостного элемента. Для определения следует рассмотреть состояние цепи до коммутации (см. рис.3.10).

Рис. 3.10. Схема для анализа докоммутационного состояния цепи

Аналогично пункту 2 ток источника тока J создает падение напряжения на параллельно соединенных сопротивлениях 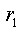и

Это же напряжение приложено к разомкнутым зажимам m, n. Используя формулу (3.16), окончательно получим

График переходного процесса для переменной 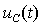представлен на рис.3.11.

Рис.3.11. График переходного процесса напряжения на емкости

Как следствие решенной задачи можно найти токи и напряжения в других элементах цепи:

а. Ток в емкости и в резистивном сопротивлении r₃

б. Напряжение на сопротивлении :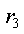

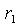
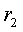
в. Напряжение на сопротивлениях и :

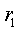
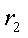
г. Токи в сопротивлениях и :

Все эти алгебраические преобразования достаточно очевидны. Полученные здесь как следствие функциональные выражения носят разрывный характер в точке t = 0 . Каждое из них можно определить непосредственно только после исследования цепи для момента времени t=0+,т.е. в первый момент после коммутации.

Рассмотренные здесь примеры показывают, что для цепей первого порядка нет необходимости составлять уравнения равновесия цепи, сводить эту систему к одному дифференциальному уравнению и решать соответствующее ему характеристическое уравнение. Достаточно найти входное резистивное сопротивление 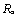со стороны реактивного элемента и воспользоваться формулой (3.11) для цепи, содержащей L, или формулой (3.14) для цепи, содержащей С.

Общий вид решения для переменных состояния также известен:

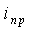
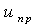
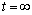
Определение и производится путем исследования стационарного состояния цепи для значений .

Численные значения i_L (0-) и u_C (0-) находятся для момента времени t=0-, который предшествует коммутации. Для каждого временного состояния цепи целесообразно составить расчетную схему замещения и, пользуясь любыми методами анализа цепи, определить требуемую переменную.

Пример 3.3. Для цепи, представленной на рис.3.12, найти закон изменения напряжения на емкости С после отключения от цепи идеального источника синусоидального напряжения

До размыкания ключа S в каждом элементе цепи протекал синусоидальный ток, обусловленный источником питающего напряжения. Емкость присоединена непосредственно к источнику напряжения, и напряжение на ней в каждый момент времени такое же, как и в источнике. К моменту коммутации это напряжение будет равно

и останется на емкости в первый момент после коммутации.

Рис. 3.12. Схема RC –цепи при питании от источника синусоидального напряжения

Переходный процесс в цепи будет развиваться за счет энергии, накопленной емкостью. В течение переходного процесса энергия электрического поля перейдет в тепловую энергию в резистивных элементах цепи. Следовательно, к концу переходного процесса напряжение на емкости станет равным нулю, что и определяет нулевое значение принужденной составляющей режима.

Проведенный предварительный анализ показывает, что переходный процесс в цепи будет определяться только свободной составляющей режима:

Постоянную времени определим по формуле (3.14), где 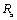найдем как

входное сопротивление цепи со стороны емкости:

💡 Видео

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать

ТОЭ - Расчет RC цепи. Найти коэффициент передачи H(jw), построить график АЧХСкачать

Линейные цепи и элементы. Дифференциальные уравнения для цепейСкачать

Урок 16. Как работает RC-цепь РЕАЛЬНО | САМОЕ ПОНЯТНОЕ ОБЪЯСНЕНИЕ!Скачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Шок! Дифференцирующие RC-цепи РЕАЛЬНО дифференцируют! Смотри пока не удалили!!!Скачать

Составление дифференциального уравненияСкачать

Переходный процесс в RC-цепи — вывод формул. Часть 1 (видео 24) | Анализ цепей | ЭлетротехникаСкачать

RC цепь - Задача │Определить показания приборовСкачать

69997 Анализ переходных процессов в RC-цепях – 1Скачать

КАК РАБОТАЕТ RC - ЦЕПЬ | ОБЪЯСНЯЮ НА ПАЛЬЦАХСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать