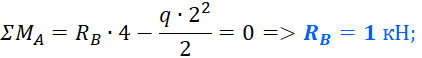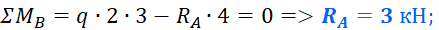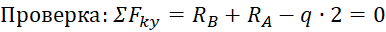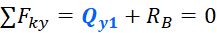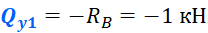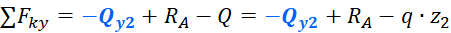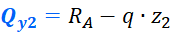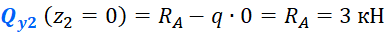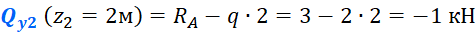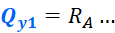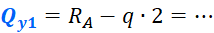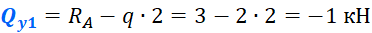Расчет эпюры и моменты уравнения

Видео:Определение реакций опор в балке. Сопромат.Скачать

Эпюра поперечных сил — как построить?

Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!

Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.

Видео:Построение эпюр в балке ( Q и M ). СопроматСкачать

Подробный способ построения эпюры поперечных сил

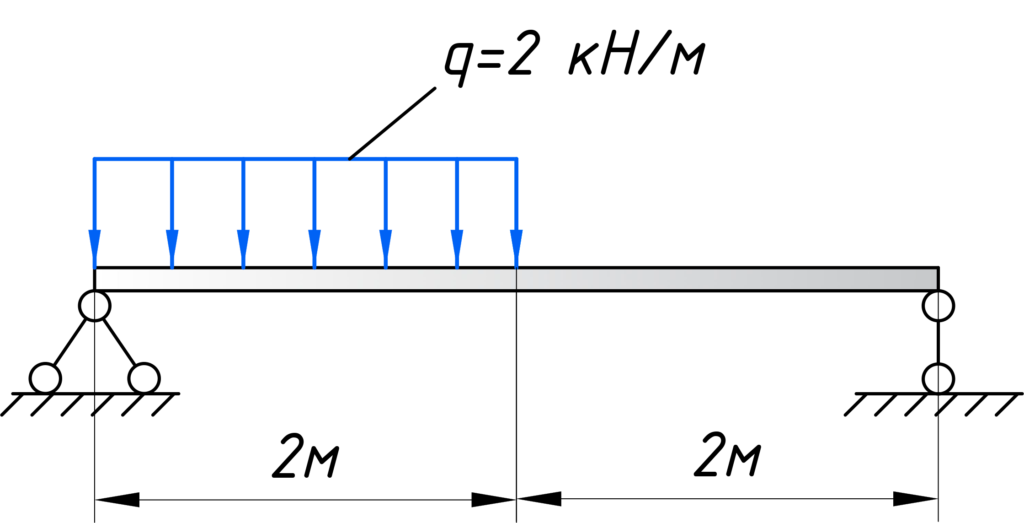
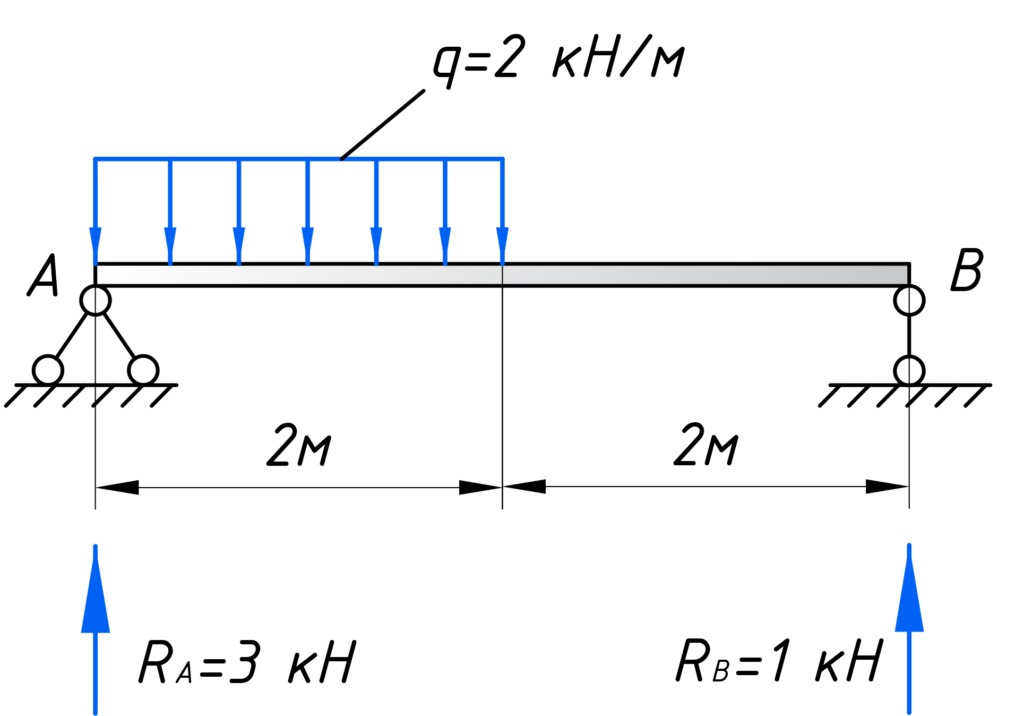
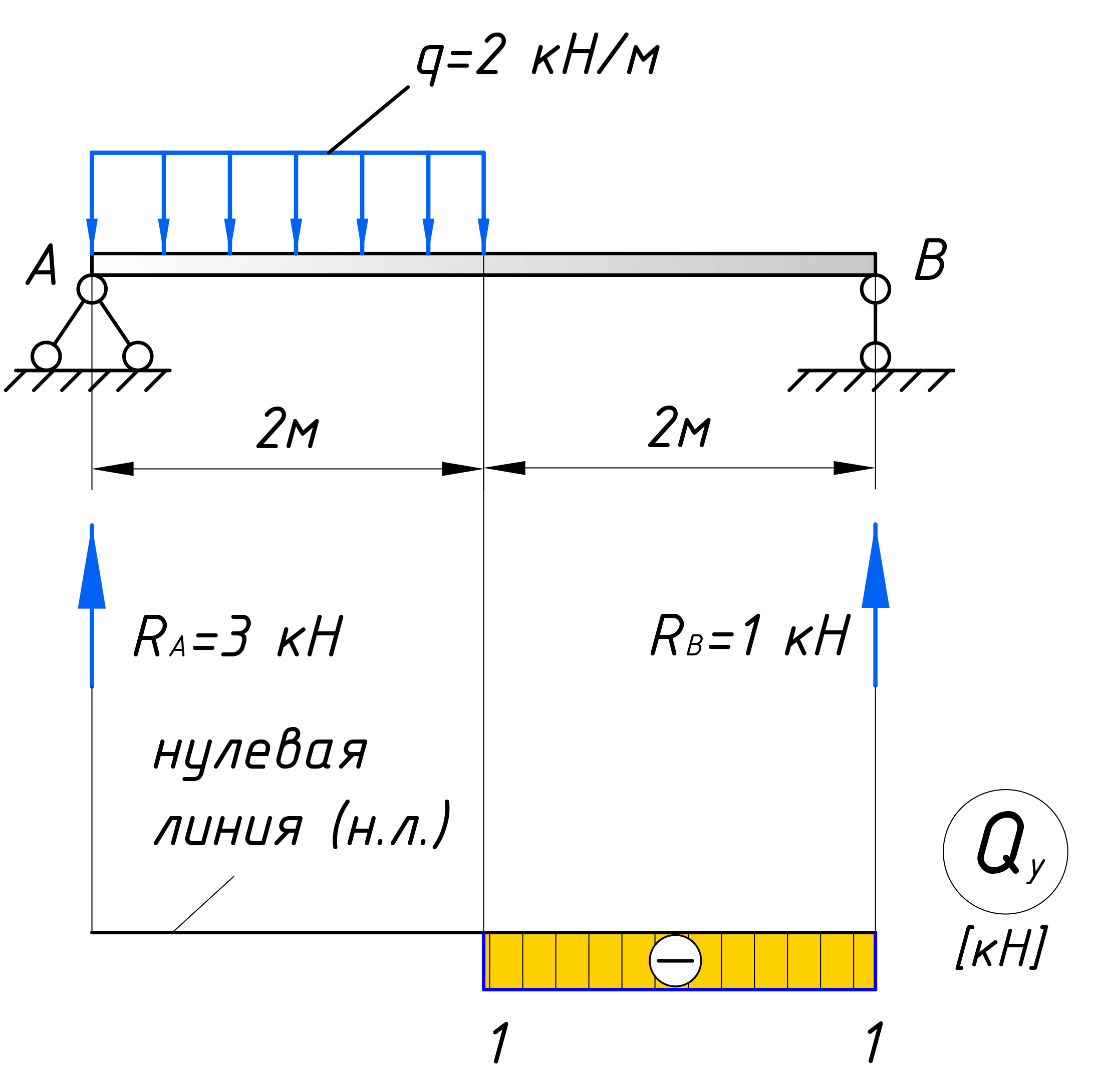
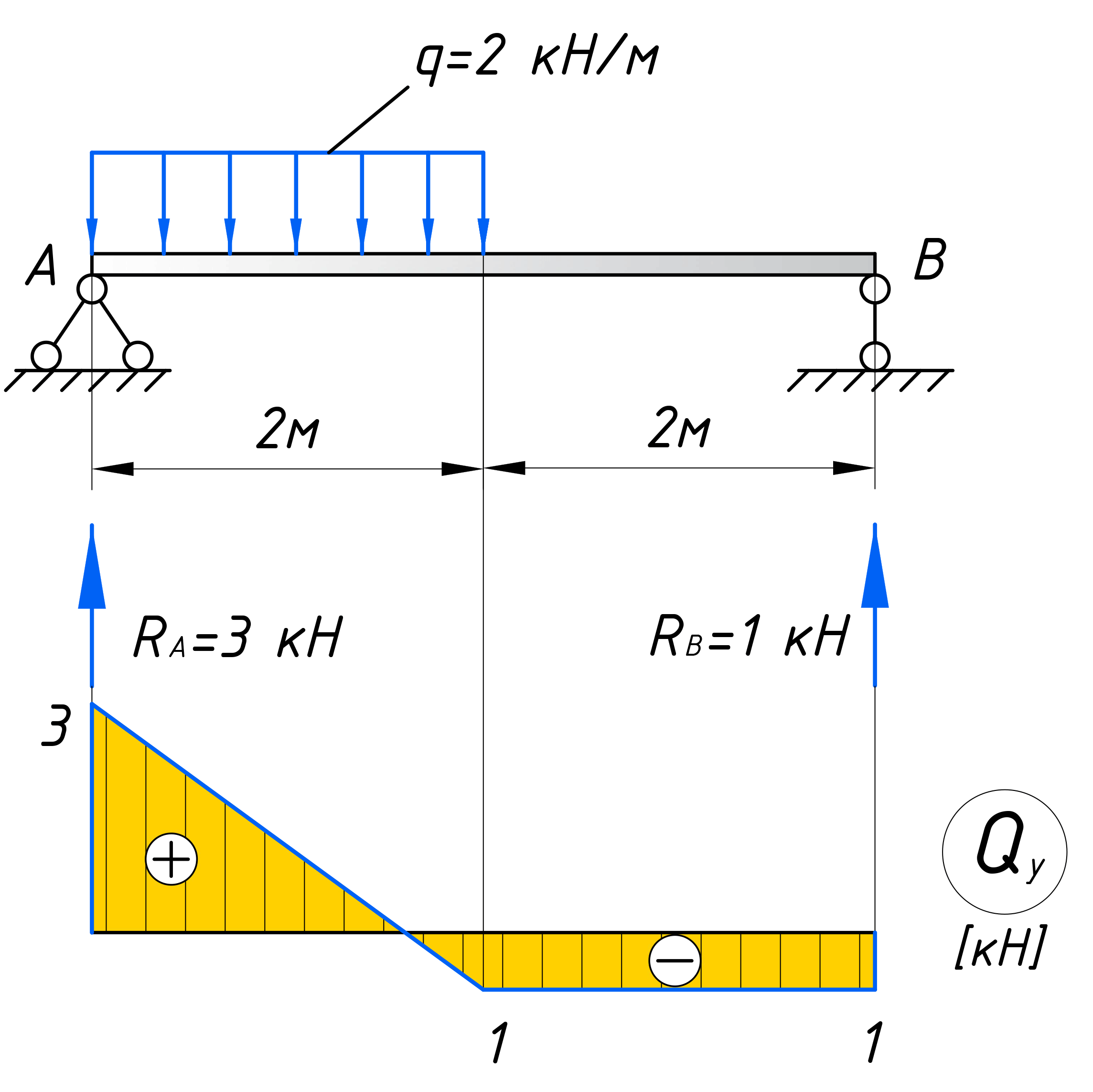
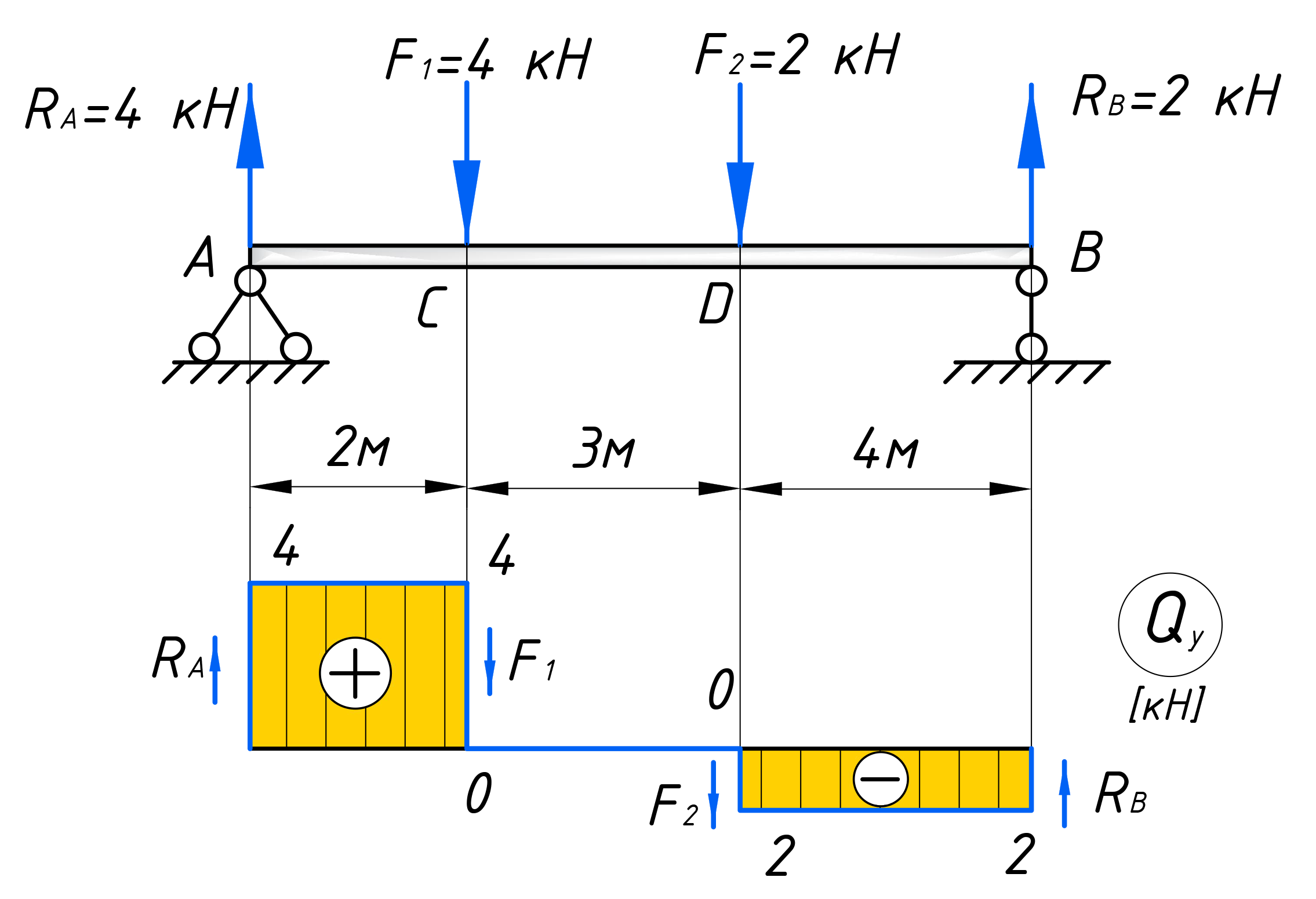
В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:

Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:

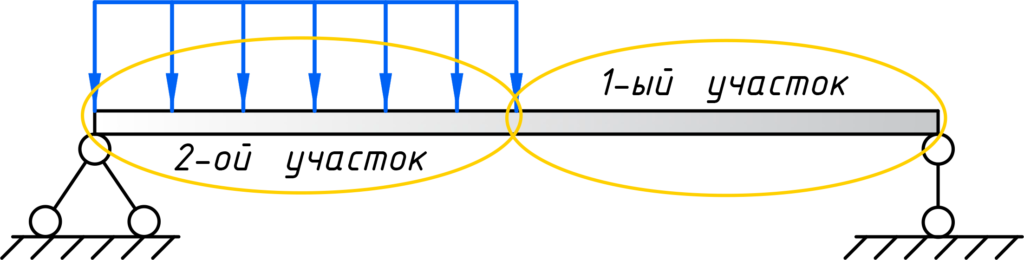
Разбиваем балку на участки

После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.

Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.

Метод сечений

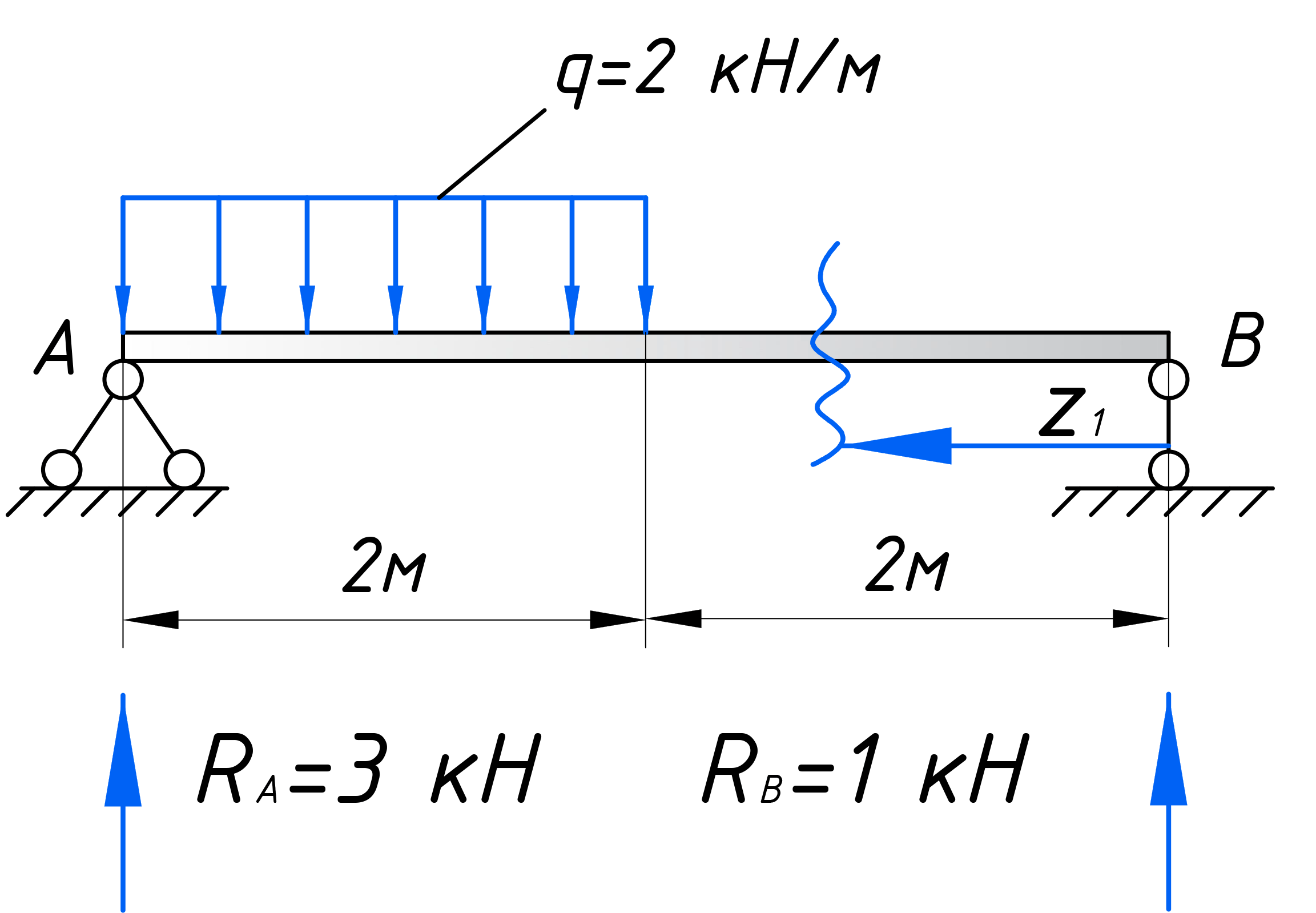
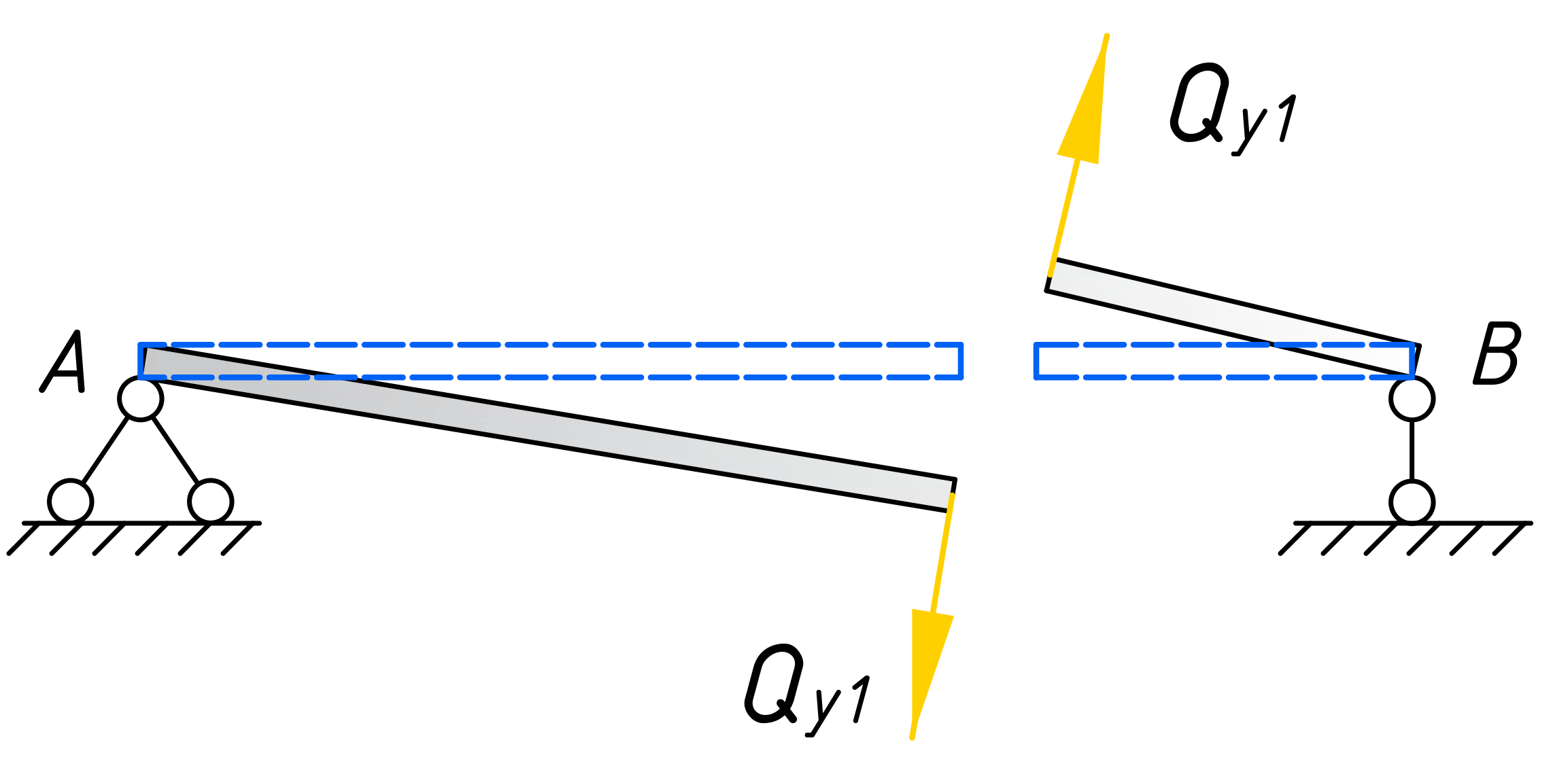
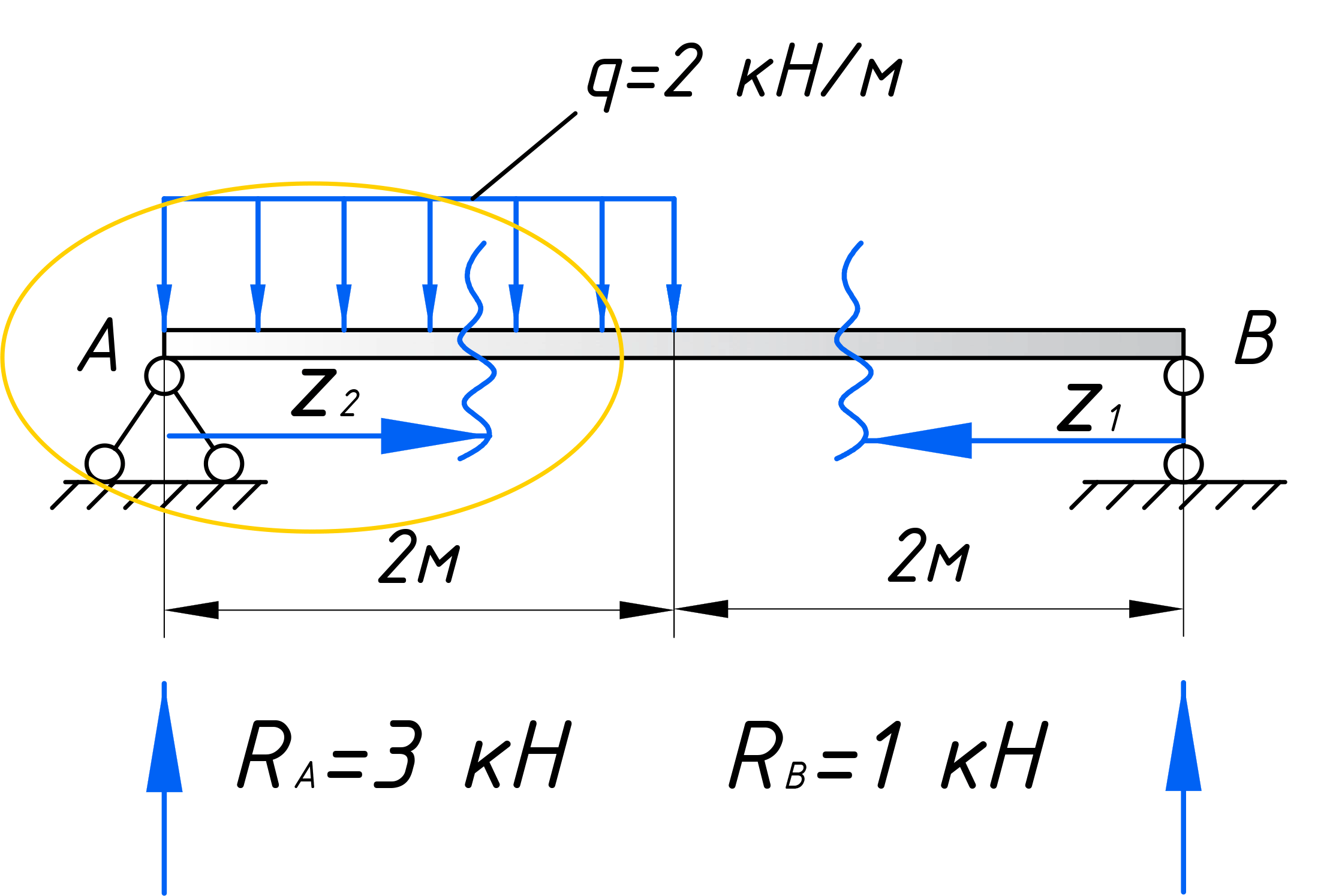
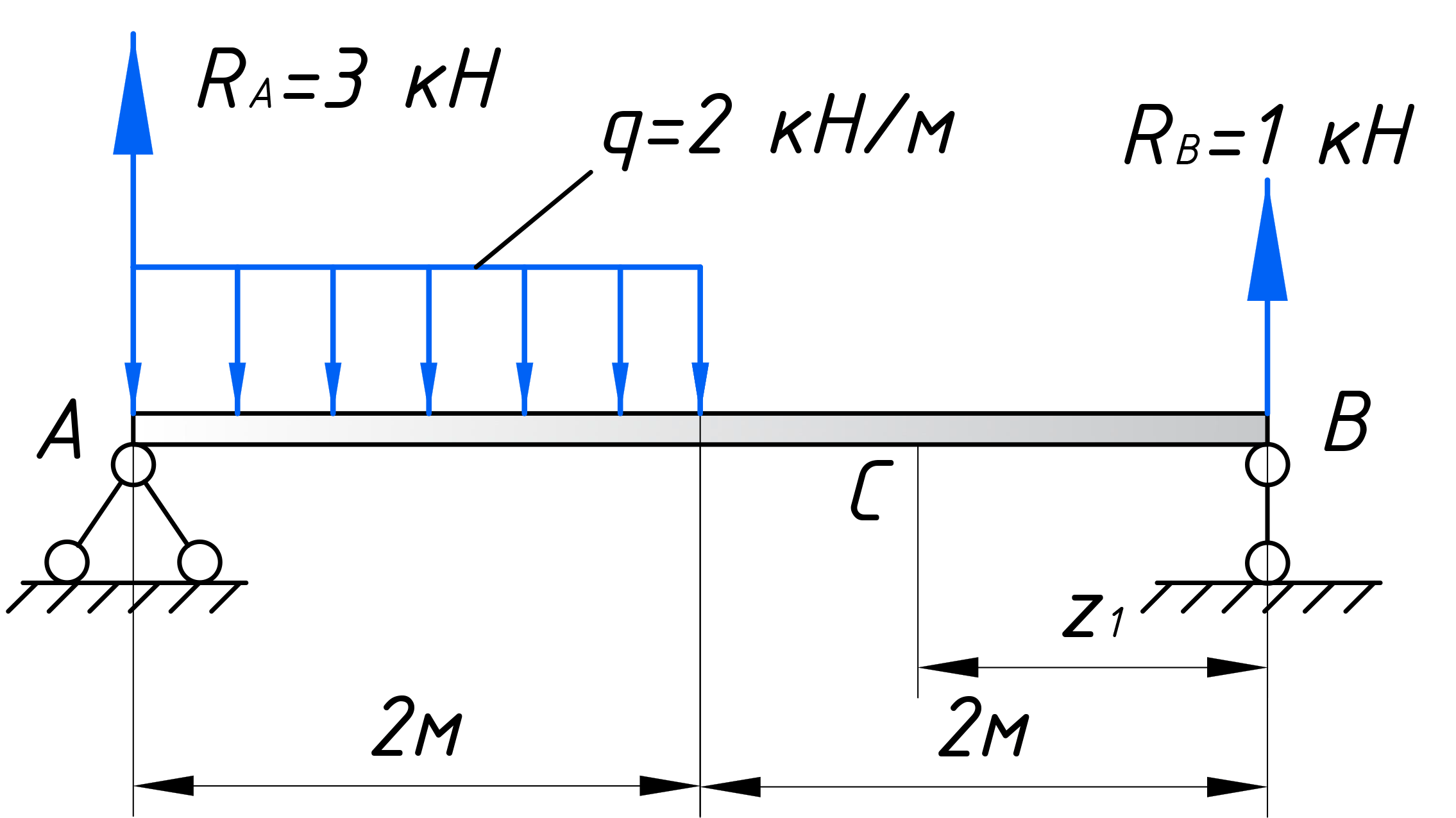
Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x₁ от правого торца балки.

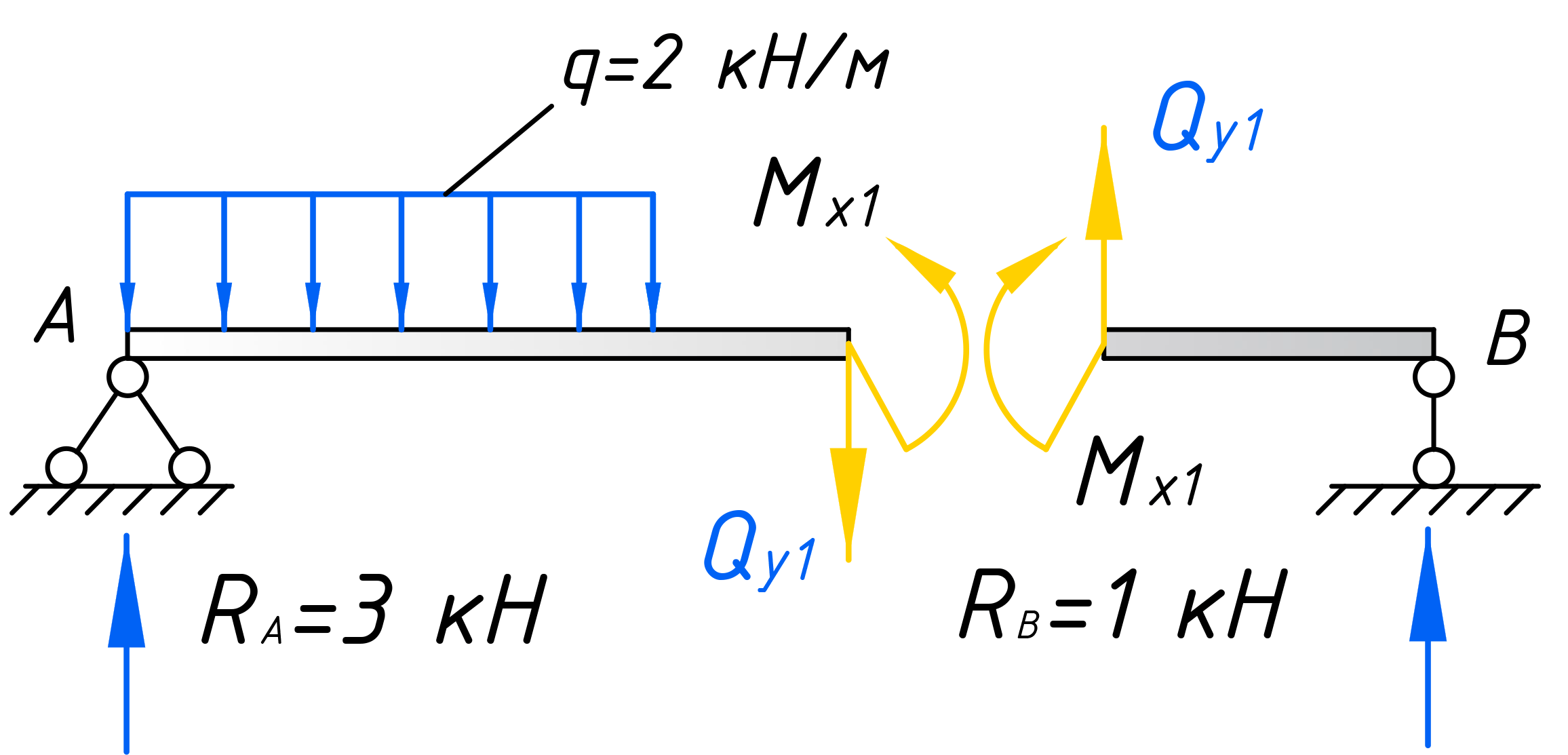
Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Q_y1 и момента M_x1. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.

Правила знаков для поперечной силы

Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.

Также многие авторы рекомендуют просто запомнить такое правило:

• Для правой отсеченной части, направлять поперечную силу вверх;
• Для левой отсеченной части, направлять поперечную силу вниз.

Вводим систему координат для первого участка

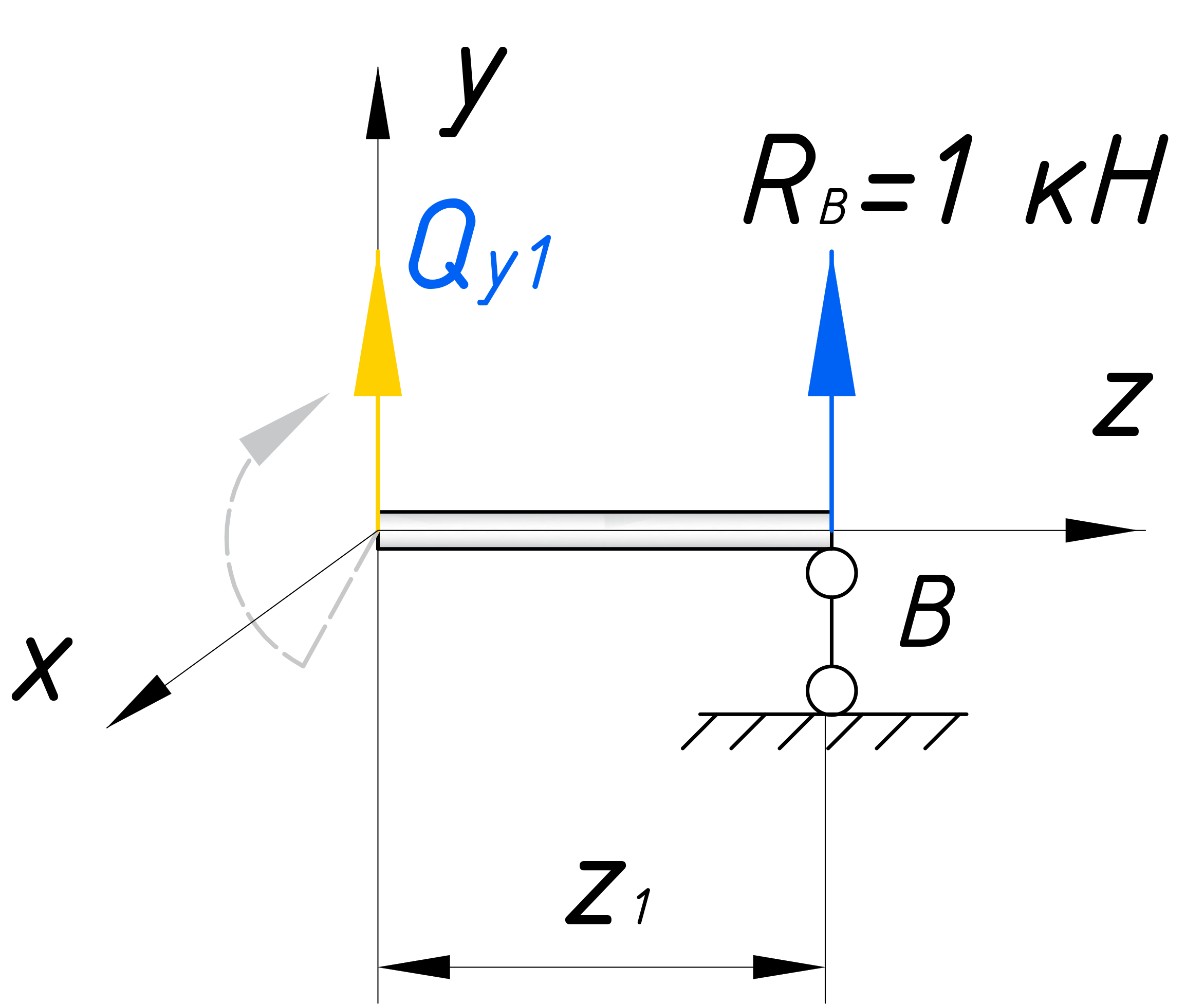
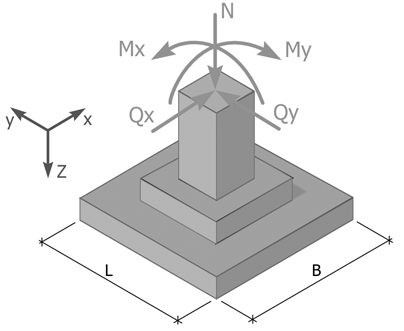
Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент M_x1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:

• Ось z будет иметь горизонтальное направление;
• Ось y будет направлена вертикально;
• Ось x будет направлена перпендикулярно плоскости чертежа (на нас).

Записываем уравнение равновесия для первого участка и строим эпюру

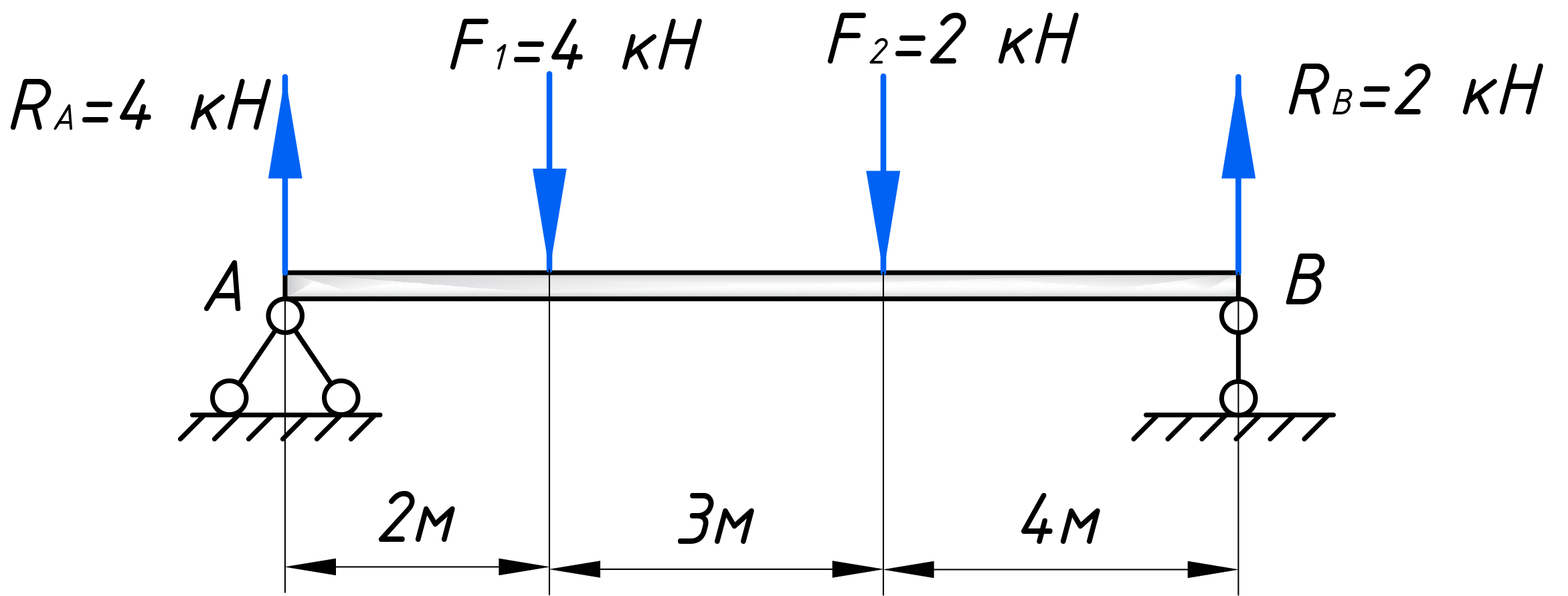
Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:

Из полученного уравнения, следует:

Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:

Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.

Расчет второго участка

Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z₂ от левого торца балки:

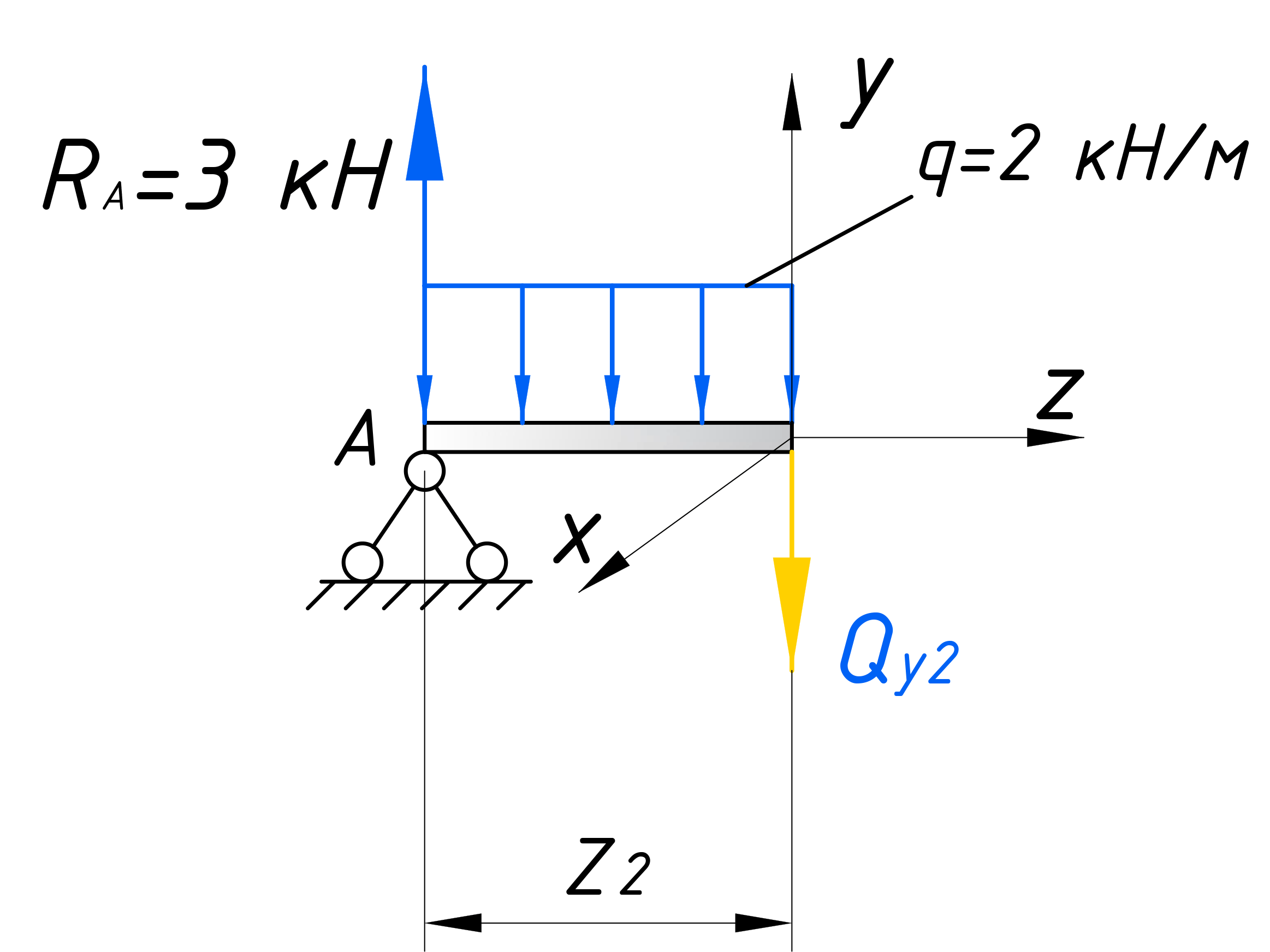
Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Q_y2 и M_x2. Вводим локальную систему координат:

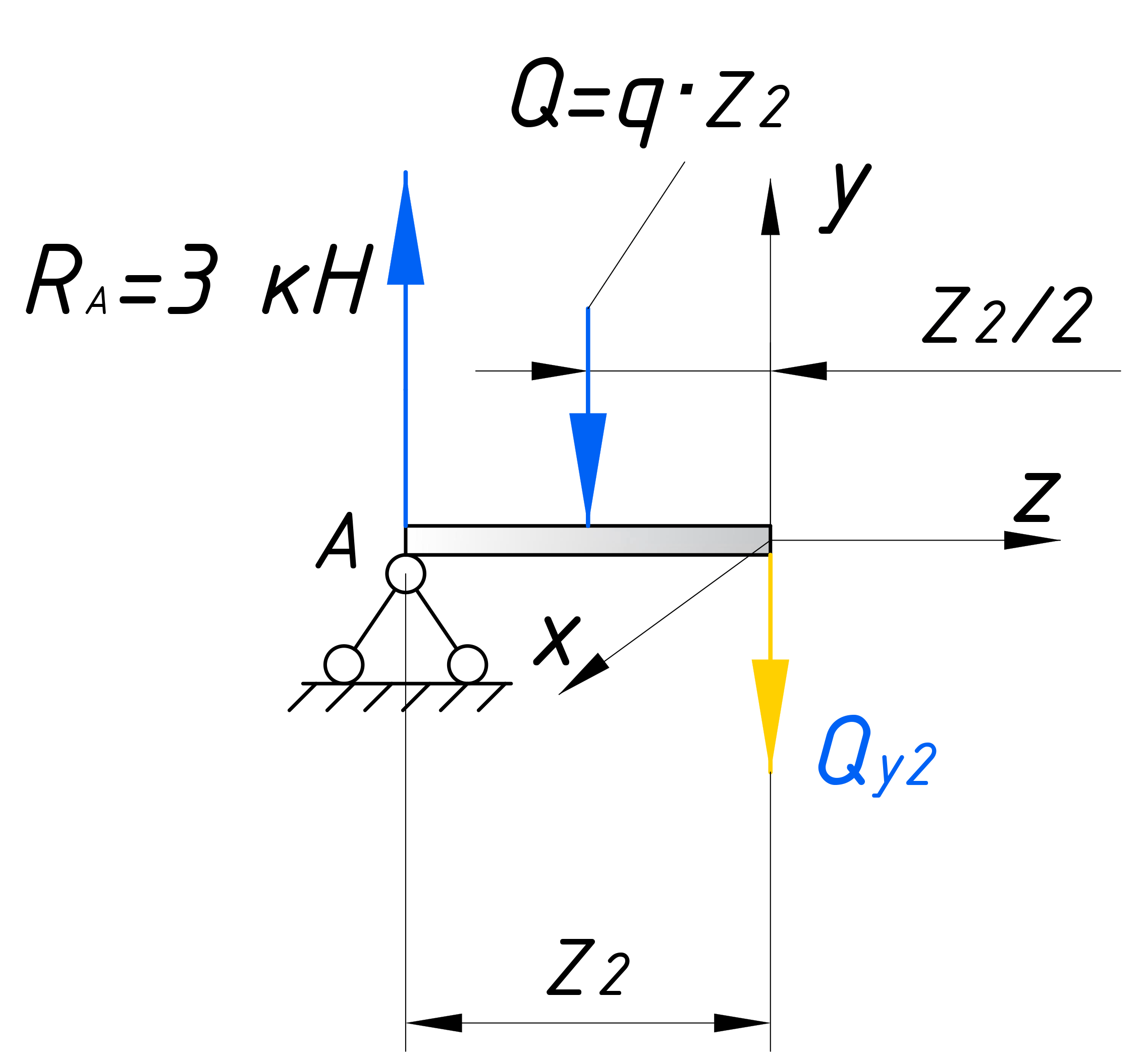
Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z₂.

Записываем уравнение равновесия для второго участка:

Выражаем поперечную силу:

Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z₂ подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z₂=0) поперечная сила будет равна:

В середине пролета, при z₂=2м получим:

По полученным значениям, строим эпюру поперечных сил на втором участке:

Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!

Видео:БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Упрощенный способ построения эпюры

Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учиться рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.

Первый участок

Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z₁. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.

Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:

• Если нагрузка относительно рассматриваемого сечения стремится повернуть ПО часовой стрелки, то в уравнении она учитывается со знаком «+»;
• Если нагрузка относительно рассматриваемого сечения стремится повернуть ПРОТИВ часовой стрелки, то в уравнении она учитывается со знаком «-».

Продемонстрирую вышеописанные правила на нашем примере. Относительно сечения С, сила R B , находящаяся справа от сечения, стремится повернуть против часовой стрелки, поэтому в уравнение она пойдет со знаком «-»:

Как видно из уравнения, поперечная сила, на первом участке, не зависит от координаты z₁, поэтому во всех сечениях она одинаковая.

Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.

Реакция R_A, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:

Нагрузку q, сворачиваем до сосредоточенной силы, как в подробном способе. Она стремится повернуться ПРОТИВ часовой стрелке, в уравнение пойдет со знаком «минус»:

Подставляя численные значения нагрузки, получим следующий результат:

Теперь перейдем ко второму участку.

Второй участок

Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:

По выполненным расчетам двух участков, можно построить уже знакомую эпюру:

Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Быстрый способ построения эпюры

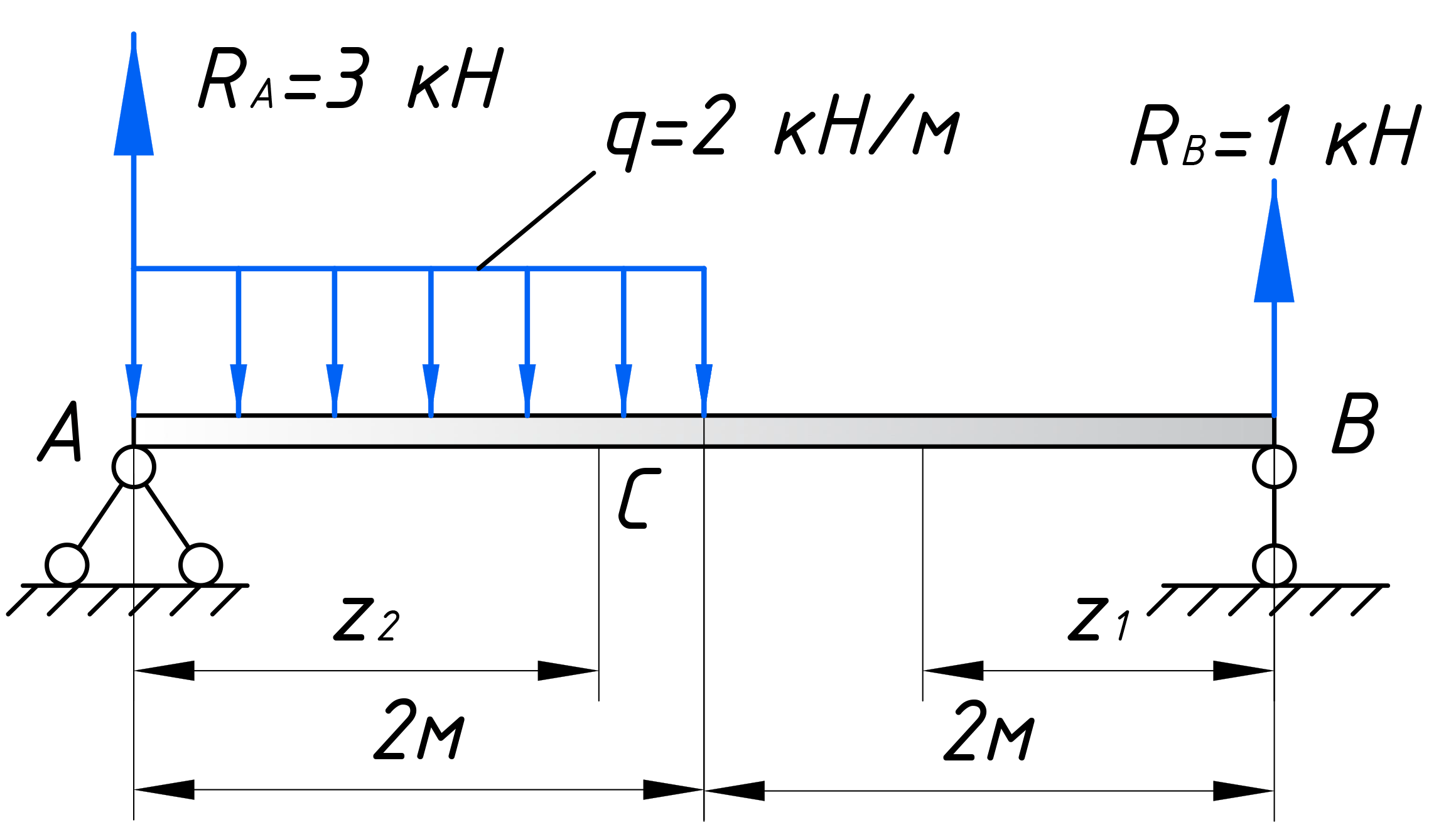
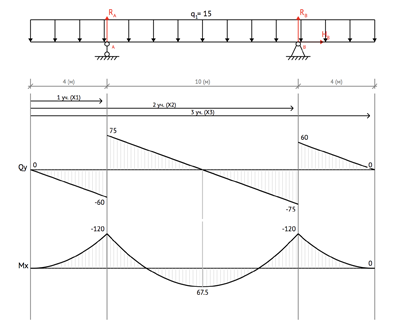
Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:

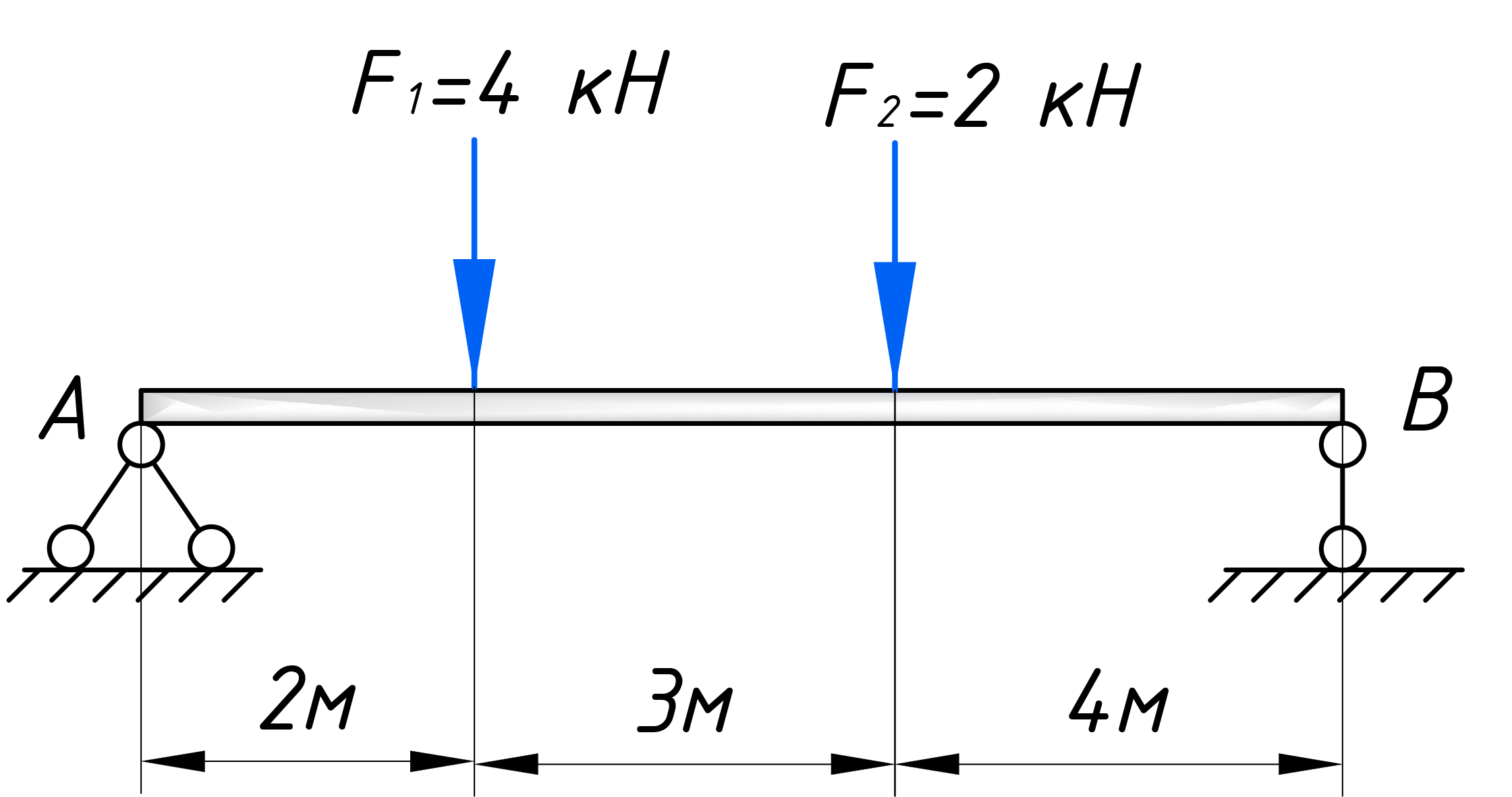
Определим для нее опорные реакции:

Расчет быстрым способом рекомендую производить слева-направо . В этом случае для скачков эпюры будут следующие правила знаков:

• Если приложенная сила направлена вверх , то и скачек на эпюре будет вверх, на величину силы;
• Если приложенная сила направлена вниз , то и скачек на эпюре будет вниз, на величину силы.

С учетом данных правил, получим вот такую эпюру поперечных сил:

Прокомментирую: в точке А, сила направлена вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направлена вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.

Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать насколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:

Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.

После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.

Видео:Уравнение трех моментов. Расчет много пролетной не разрезной балкиСкачать

SOPROMATGURU — облачный сервис для выполнения онлайн расчетов балок, рам, ферм и построения эпюр моментов, поперечных и продольных сил

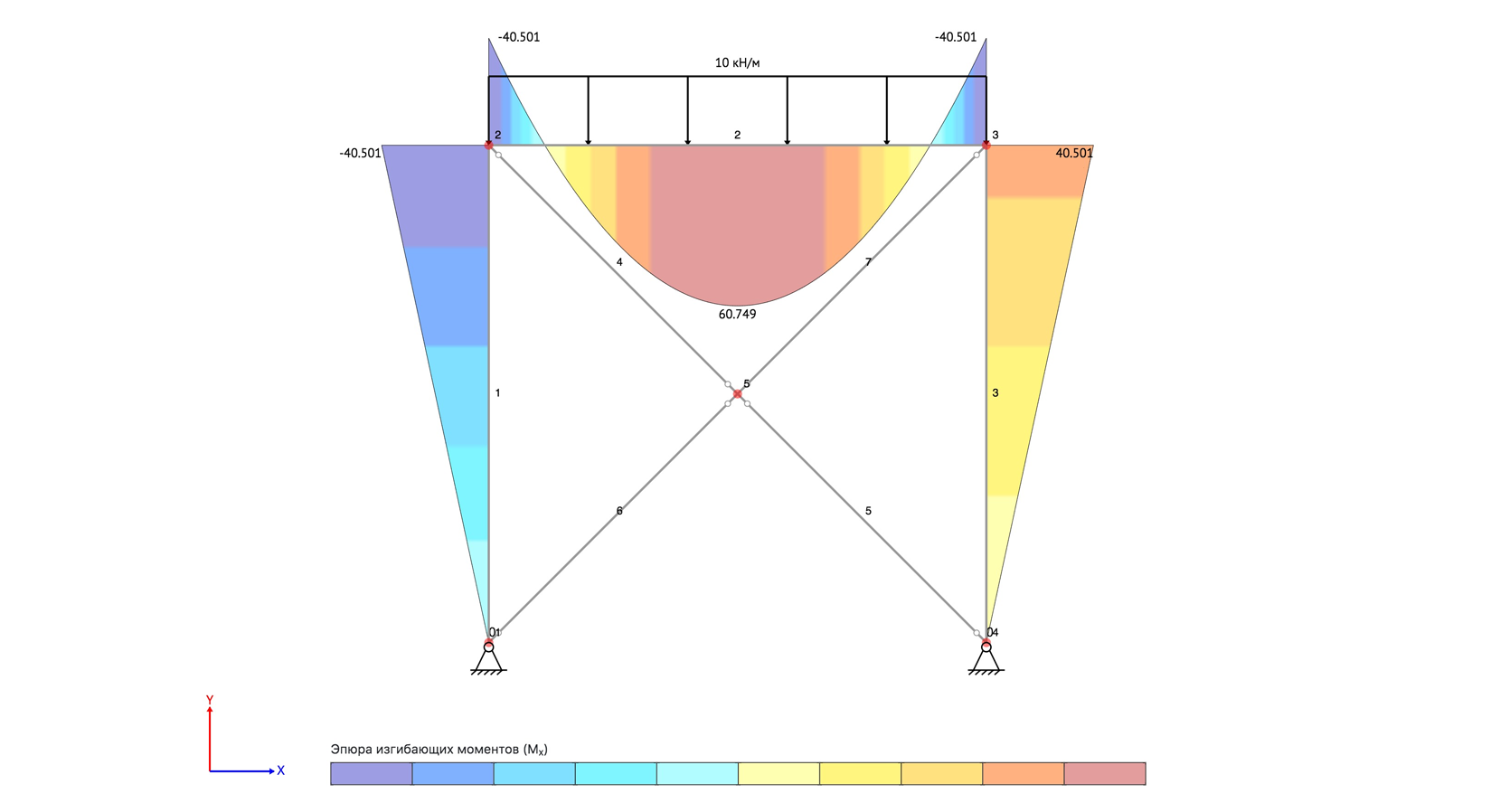
SOPROMATGURU — облачный сервис для выполнения онлайн расчетов балок, рам, ферм и построения эпюр моментов, поперечных и продольных сил.

Расчет статически-определимых балок с подробным отчетом — примеры

Онлайн-сервис позволяет в автоматическом осуществлять расчет статически-определимых балок методом сечений с формированием подробного отчета о ходе решения. Существует возможность автоматического подбора сечения балки по критериям прочности (проверка по нормальным и касательным напряжениям, по третьей теории прочности) для статически-определимых балок.

Расчет статически-неопределимых балок, рам и ферм

Калькулятор расчета балок позволяет рассчитывать внутренние усилия также и в статически-неопределимых балках и рамах методом конечных элементов. Результат расчета конструкции методом конечных элементов не содержит подробного отчета о ходе нахождения внутренних усилий конструкции.

Расчет геометрических характеристик сечений — пример отчета

Конструктор сечений дает возможность конструировать пользовательские составные сечения как из прокатных профилей (двутавр, швеллер, тавр, квадратная труба и др.), выбранных из сортамента, так и выбрав произвольные параметрические сечения. Онлайн-сервис позволяет формировать подробный отчет о ходе расчета таких геометрических характеристики как: площадь сечения, координаты центра тяжести, статические моменты, моменты инерции и моменты сопротивления.

Расчет столбчатых и ленточных фундаментов — пример отчета

Модуль расчета фундаментов позволяет подбирать и проверять заданные габариты столбчатых и ленточных фундаментов с учетом расчетного сопротивления грунта основания, контактных напряжений, эксцентриситетов и деформации основания. Осуществляется конструирование фундаментов. Все расчеты выгружаются в подробный отчет.

Видео:Построение эпюр поперечных сил и изгибающих моментов в балке.Скачать

ПроСопромат.ру

Видео:Построение эпюр поперечных сил и изгибающих моментов в многопролетных шарнирно-консольных балках.Скачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Расчет значений Q и M для построения эпюр поперечных сил и изгибающих моментов балки на двух опорахСкачать

Архив рубрики: Задачи на эпюры

Видео:РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать

Построение эпюр внутренних силовых факторов в раме

Задача. Расчет рамы. Для рамы построить эпюры продольных сил N, поперечных сил Q и изгибающих моментов М.

1. Определим опорные реакции

Нанесем значения опорных реакций на расчетную схему.

2. Строим эпюру продольных сил N методом сечений. Имеем три характерных участка и три сечения на них.

Правило знаков продольных сил – продольная сила считается положительной, если сила растягивает стержень, и отрицательной, если сила сжимает стержень. Положительные значения откладываем влево от стойки и вверх от ригеля.

Строим эпюру продольных сил.

3. Строим эпюру поперечных сил Q методом сечений. Правило знаков – если сила относительно сечения направлена по часовой стрелке, то поперечная сила считается положительной и наоборот. Положительные значения откладываются влево от стоек и вверх от ригеля.

Строим эпюру поперечных сил

4. Строим эпюру изгибающих моментов М методом характерных точек. Расставляем точки: А – опора, В,С, — узлы рамы, D – свободный конец, К – середина равномерно распределенной нагрузки (точки экстремума при построении эп.Q не обнаружено). Эпюру М строим на сжатых волокнах (для машиностроительных специальностей), знак не ставим.

Строим эпюру моментов.

5. Вырезаем узлы С и В и проверяем их равновесие.

Узлы находятся в равновесии, значит эпюры построены верно.

Видео:Аскаридоз лошадейСкачать

Задача

Для балки с жесткой заделкой построить эпюры Q и М.

Расставляем сечения от свободного конца балки — в этом случае можно построить эпюры, не определяя опорных реакций. Рассматривать в каждом случае будем правую часть — справа от сечения. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 2 участка, 2 сечения.

Сечение 2-2 проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z₂ вправо от сечения до начала участка. Определяем поперечные силы в сечениях. Правило знаков см. — здесь.

Строим эпюру Q.

Построим эпюру М методом характерных точек. Расставляем точки на балке — это точки начала и конца балки (D,A), сосредоточенного момента (B), а также отметим в качестве характерной точки середину равномерно распределенной нагрузки (K) — это дополнительная точка для построения параболической кривой.

Определяем изгибающие моменты в точках. Правило знаков см. — здесь.

Момент в т. В будем определять следующим образом. Сначала определим:

Точку К возьмем в середине участка с равномерно распределенной нагрузкой.

Строим эпюру M. Участок АВ – параболическая кривая (правило «зонтика»), участок ВD – прямая наклонная линия.

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Задача на построение эпюр Q и M в балке

Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

1. Обозначаем опоры буквами Аи В и направляем опорные реакции R_А и R_В.

Составляем уравнения равновесия.

Проверка

Записываем значения R_А и R_В на расчетную схему.

2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1 ход слева.

Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z₁ влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.

сеч. 2-2 ход справа.

Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z₂ вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.

сеч. 3-3 ход справа.

сеч. 4-4 ход справа.

Строим эпюру Q.

3. Построение эпюры М методом характерных точек.

Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.

Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.

Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z₂ равняется неизвестному х.

Теперь, зная х, определим момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

Видео:ЭПЮРЫ. МЕТОД ТОЧЕК. СОПРОМАТ ДЛЯ СТРОИТЕЛЬНЫХ СПЕЦИАЛЬНОСТЕЙ. Балка.Скачать

Задача на построение эпюр поперечной силы Q, изгибающего момента M и подбор сечения (проектный расчет)

Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.

Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м

Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.

1. Определим опорные реакции.

Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН

В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.

Найдем вертикальную реакцию опоры R_A и опорный момент М_A из уравнений равновесия.

На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции R_A.3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз.

4.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения

Таким образом, подбираем сечение с диаметром 25 см.

Видео:Расстановка Коэффициентов в Химических Реакциях // Подготовка к ЕГЭ по ХимииСкачать

Построение эпюр Q и М , проектный расчет (подбор сечения)

Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.

1.Определение реакций:

Сумма моментов относительно опор:

Опора А:

Опора В:

Сумма проекций всех сил на ось У (проверка):

2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.

1) Первый участок:

2) Второй участок:

3) Третий участок:

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:

С эпюры берем максимальный момент:

По сортаменту подбираем двутавр № 20 с

Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:

Видео:Структурный анализ, поэтажная схема, эпюры моментов и сил много пролетной балкиСкачать

Построение эпюр Q и М, проектировочный расчет (подбор сечения)

Для заданной балки требуется построить эпюры Q и M, найти M_max и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала R_u=10 МПа.

1.Определение реакций:

Сумма проекций всех сил на ось z:

Сумма проекций всех сил на ось y:

Сумма моментов относительно точки А:

После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).

2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.

Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.

M— изгибающий момент, считается положительным, если растягивает нижние волокна.

1)Первый участок:

2) Второй участок:

3) Третий участок:

Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.

Подберем деревянную балку круглого поперечного сечения при R_u=10 МПа

С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.

Видео:ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!Скачать

Построение эпюр в балке с шарниром

Задача 1. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.

Если рассмотреть левую часть, то в уравнении будут присутствовать две неизвестные R_А и М_А. Значит, следует рассмотреть правую часть (из него найдем R_В).

Теперь из него найдем М_А

Следующее уравнение из него найдем R_А

2. Строим эпюру Q.

Участок первый — АС, смотрим левую часть

Участок второй — СВ, смотрим правую часть

3. Строим эпюру М

Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. М_К , для этого определим положение точки К.

Это уравнение первого участка, на котором находится точка К

в точке К

Строим эпюры. Задача решена.

Задача 2. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.

Если рассмотреть правую часть, то в уравнении будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.

Знак «-» говорит о том, что реакция R_В направлена в обратную сторону.

Проверка:

2. Построение эпюры Q.

Участок первый — ЕА, смотрим левую часть

Участок второй — АС, смотрим левую часть

Участок третий — СВ, смотрим левую часть

Участок четвертый — ВД, смотрим правую часть

3. Построение эпюры М

Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД

Строим эпюры, задача решена.

Видео:Построение эпюр при изгибе. Часть 1. Консольная балкаСкачать

Построение эпюр в рамах

Задача 1. Построить эпюры внутренних усилий для рамы ( рис.а).

Дано: F=30кН, q=40 кН/м, М=50кНм, а=1,8м, h=2м.

Решение.

Для рассматриваемой рамы опорные реакции можно не определять, поскольку будем рассматривать участки, идя от свободных концов рамы к заделке.

Вычислим значения внутренних усилий N, Q и М в характерных сечениях рамы. Правило знаков для поперечных сил Q и изгибающих моментов М такие же,как в балках. Эпюры моментов построим на сжатых волокнах. Для продольной N, силы правило знаков: растягивающая сила – положительна, сжимающая – отрицательна.

Участок ВС: (сжаты нижние волокна).

(сжаты нижние волокна).

Участок DC: (сжаты верхние волокна).

Участок СК: (сжаты левые волокна)

(сжаты левые волокна)

На рисунке — эпюры нормальных (продольных) сил — (б), , поперечных сил — (в) и изгибающих моментов — (г).

Проверка равновесия узла С:

Задача 2 Построить эпюры внутренних усилий для рамы (рис. а).

Дано: F=30кН, q=40 кН/м, М=50кНм, а=3м, h=2м.

Определим опорные реакции рамы:

Из этих уравнений найдем:

Поскольку значения реакции R_K имеет знак минус, на рис. а изменяется направление данного вектора на противоположное, при этом записывается R_K=83,33кН.

Определим значения внутренних усилий N, Q и М в характерных сечениях рамы:

Участок ВС:

(сжаты правые волокна).

Участок CD:

(сжаты правые волокна);

(сжаты правые волокна).

Участок DE:

(сжаты нижние волокна);

(сжаты нижние волокна).

Участок КС

(сжаты левые волокна).

Построим эпюры нормальных (продольных) сил (б), поперечных сил (в) и изгибающих моментов (г).

Рассмотрим равновесие узлов D и Е

Из рассмотрения узлов Dи Е видно, что они находятся в равновесии.

Задача 3. Для рамы с шарниром построить эпюры внутренних усилий.

Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.

Решение. Определим опорные реакции. Следует отметить ,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых ,так и от правых сил равен нулю. Рассмотрим левую часть.

Уравнения равновесия для рассматриваемой рамы можно записать в виде:

Из решения данных уравнений следует:

На схеме рамы направление действия силы Н_В изменяется на противоположное (Н_B=15кН).

Определим усилия в характерных сечениях рамы.

Участок BZ:

(сжаты левые волокна).

Участок ZC:

(сжаты левые волокна);

Участок КD:

(сжаты левые волокна);

(сжаты левые волокна).

Участок DС:

(сжаты нижние волокна);

Определение экстремального значения изгибающего момента на участке CD :

(сжаты верхние волокна).

Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы.

Узлы C и D находятся в равновесии.

Видео:Вот для чего нужно строить эпюры в сопромате!Скачать

Задача 8

Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции V_A; С – точка приложения сосредоточенной силы; D, B– начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:

Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис,б).

2. Построение эпюры моментов

Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка при­ложения сосредоточенного момента и силы F; D и В — начало и конец действия рав­номерно распределенной на­грузки. Поскольку эпюра Q_x на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.

Ходом справа находим M_B = 0.

По найденным значениям строим эпюру изгибающих моментов (см. рис. в).

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

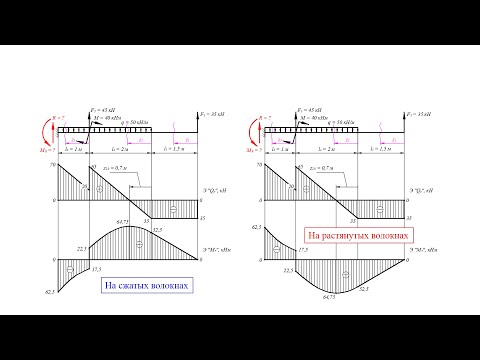
Задача 7

Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры Q_у. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Q_у ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Q_у в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно .

Строим эпюру Q_у методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:

Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Q_у. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Q_у (рис. б).

Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, рав­ный значению силы. Если наклонная линия под распределенной на­грузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Q_у и М_x, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпю­ре Q_у себя никак не проявляет, так как сумма проекций сил, образую­щих пару, равна нулю.

2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, ме­тодом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значе­ния изгибающих моментов в начале участка, конце его и в одном проме­жуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в кото­ром эпюра Q_у пересекает нулевую линию, т.е. где Q_у= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Q_у не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если на­грузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпю­ры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и бу­дет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.

Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточ­ных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствую­щих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соот­ветствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.

Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Q_у = 0.

Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Q_у (рис.б).

Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).