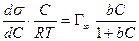Расчет адсорбции по уравнению гиббса (4 видео)

Содержание

УРАВНЕНИЕ АДСОРБЦИИ ГИББСА
Лекция 13. Адсорбция
1.7. Определение адсорбции ПАВ на поверхности водных растворов
🔍 Видео

Видео:Адсорбция на поверхностях растворовСкачать

УРАВНЕНИЕ АДСОРБЦИИ ГИББСА

Выше (п. 2.4) мы пришли к выводу, что процесс адсорбции обусловлен снижением поверхностного натяжения. Очевидно, чем в большей степени ПАВ снижает поверхностное натяжение, тем большей должна быть его адсорбция. Напротив, ПИВ должна быть присуща отрицательная адсорбция.

Исходя из второго закона термодинамики американский ученый Дж. Гиббс в 70–х гг. XIX в. вывел важное уравнение, связывающее величину адсорбции со способностью растворенного вещества изменять поверхностное натяжение раствора:

(3.1)

где Г_i, – избыточная адсорбция i-го компонента (см. 2.10), c_i – его молярная концентрация в растворе, Т – температура, при которой происходит адсорбция, R – газовая постоянная, – изменение поверхностного натяжения раствора при изменении концентрации на dc_i.

В такой форме уравнение Гиббса применяется для разбавленных растворов. Вы, очевидно, помните, что для концентрированных растворов концентрацию нужно заменить активностью:

(3.2)

Уравнение Гиббса было выведено теоретически. В дальнейшем оно было подтверждено экспериментально Мак–Беном методом среза тонких слоев с последующим их химическим анализом. Аналогичные исследования были проведены Сазаки с использованием метода радиоактивных индикаторов.

Проанализируем уравнение Гиббса.

Если 0, т. е. наблюдается положительная избыточная адсорбция – i–е вещество концентрируется на поверхности раствора; если >0, то Г_i

Рис. 3.2. Определение избыточной адсорбции

Рис. 3.3. Изотерма адсорбции

Значение избыточной адсорбции для любой концентрации

с_i		Z_i	Г_i	с_i		Z_i	Г_i
c₁	₁	Z₁	Г₁	c₄	₄	Z₄	Г₄
c₂	₂	Z₂	Г₂	…	…	…	…
c₃	₃	Z₃	Г₃	…	…	…	…

ПОВЕРХНОСТНАЯ АКТИВНОСТЬ.

ПРАВИЛО ДЮКЛО-ТРАУБЕ

Из уравнения Гиббса следует, что характеристикой поведения вещества при адсорбции является величина производной , однако ее значение изменяется при изменении концентрации (см. рис. 3.2). Чтобы придать этой величине вид характеристической постоянной, берут ее предельное значение (при с 0). Эту величину П. А. Ребиндер (1924) назвал поверхностной активностью g:

(3.4)

[g] = Дж–м 3 /м 2 -моль = Дж–м/моль или Н-м 2 /моль.

Чем в большей степени уменьшается поверхностное натяжение с увеличением концентрации адсорбируемого вещества, тем больше поверхностная активность этого вещества, и тем больше его гиббсовская адсорбция.

Поверхностную активность можно определить графически как отрицательное значение тангенса угла наклона касательной, проведенной к кривой =f(c) в точке ее пересечения с осью ординат.

Таким образом, для ПАВ: g > 0; 0. Для ПИВ: g 0, Г_i

2. В гомологическом ряду прослеживаются четкие закономерности в изменении поверхностной активности (g): она возрастает по мере увеличения длины углеводородного радикала.

На основании большого экспериментального материала в конце XIX в. Дюкло и Траубе сформулировали правило:

Поверхностная активность предельных жирных кислот в водных растворах возрастает в 3–3,5 раза при удлинении углеводородной цепи на одно звено (группу –CH₂).

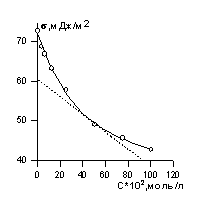
На рис. 3.4 приведены изотермы поверхностного натяжения для ряда кислот.

Рис.3.4. Изотерма поверхностного натяжения некоторых кислот

1 – СН₃СООН – уксусная кислота (n_с=1); 2 – СН₃СН₂СООН – пропионовая кислота (n_с =2); 3 – СН₃(СН₂)₂СООН – масляная кислота (n_с =3); 4 – СН₃(СН₂)₃СООН – изовалериановая кислота (n_с = 4); 5 – СН₃(СН₂)₄СООН – капроновая кислота (n_с =5); n_с – число атомтов С в углеводородном радикале.

Рис. 3.6 Ориентация молекул ПАВ на поверхности водного раствора

а – при малых концентрациях; б – при умеренных концентрациях; в – в насыщенном адсорбционном слое.

При малых концентрациях углеводородные цепи, вытолкнутые в воздух, «плавают» на поверхности воды, тогда как полярная группа погружена в воду (рис. 3.6а), такое положение возможно из-за гибкости углеродной цепи. С ростом концентрации число молекул в поверхностном слое увеличивается, цепи поднимаются. Какие-то из них принимают вертикальное положение (рис. 3.6б). В насыщенном адсорбционном слое поверхность воды оказывается сплошь покрытой «частоколом» из вертикально ориентированных молекул ПАВ (рис. 3.6в), значение поверхностного натяжения в этом случае приближается к значению, характерному для чистого жидкого ПАВ на границе с воздухом.

Из-за вертикальной ориентации молекул ПАВ в поверхностном слое максимальная адсорбция ( ) не зависит от длины «хвоста» (углеводородного радикала), а определяется только размерами поперечного сечения молекулы, которые в гомологическом ряду остаются неизменными.

Экспериментально найденная величина дает возможность рассчитать поперечный размер молекулы (S_o).

Предельная избыточная адсорбция ПАВ равна:

(3.5)

где – количество ПАВ в поверхностном слое. Так как поверхностный слой полностью заполнен молекулами ПАВ,

(3.6)

где N_a — число Авогадро.

Подставляя полученное значение S_1,2 в уравнение (3.5), получаем

или (3.7)

Так было найдено, что поперечный размер S_o молекул всех жирных кислот равен 20 * 10 -16 см 2 , а предельных спиртов – 25 * 10 -16 см 2 . Из величины предельной адсорбции была найдена также длина молекулы .

Масса 1 см 2 поверхностного слоя равна

, (3.8)

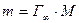
где М – молярная масса ПАВ.

В то же время плотность

, (3.9)

так как объем 1 см 3 поверхностного слоя равен . Из формул (3.8) и (3.9) следует:

(3.10)

Экспериментальные данные показали, что длина молекулы ПАВ пропорциональна числу атомов углерода в углеводородном радикале n_с, и нм для всего ряда. Величина 0,13 нм близка к диаметру атома углерода.

Таким образом, размеры молекул впервые в истории химии были определены коллоидно-химическим методом. В дальнейшем эти результаты были подтверждены другими методами.

УРАВНЕНИЕ ШИШКОВСКОГО

В 1908 г. киевский ученый Б. А. Шишковский эмпирическим путем получил уравнение, связывающее поверхностное натяжение водных растворов ПАВ с их концентрацией:

(3.11)

где – поверхностное натяжение воды; – поверхностное натяжение раствора; с – концентрация раствора; В – константа, мало зависящая от природы ПАВ внутри данного гомологического ряда; К – удельная капиллярная постоянная, которая увеличивается в 3–3,5 раза при удлинении углеводородного радикала на одно звено (группу –СН₂–).

Для того чтобы выяснить физический смысл постоянной В, обратимся к.уравнению Гиббса:

или

Разделим переменные и примем, что

Интегрируем это уравнение, принимая во внимание, что . – величина постоянная:

(3.12)

где А – постоянная интегрирования.

Уравнение (3.12) получено в результате преобразования уравнения Гиббса для предельной адсорбции. Теперь для этих же условий запишем уравнение Шишковского, принимая во внимание, что максимальная адсорбция может быть достигнута при достаточно больших концентрациях ПАВ.

Тогда с >> 1, Кс >> 1 и 1 + Кс Кс и

(3.13)

Сравнивая уравнения (3.13) и (3.12), видим, что

(3.14)

Теперь становится понятным, почему величина В в уравнении Шишковского остается постоянной в пределах одного гомологического ряда.

Однако смысл удельной капиллярной постоянной К пока остается неясным

ТЕОРИЯ МОНОМОЛЕКУЛЯРНОЙ

АДСОРБЦИИ ЛЕНГМЮРА

Отметим основные положения этой теории.

1. Адсорбция мономолекулярна.

2. При адсорбции устанавливается динамическое равновесие, которое можно рассматривать как квазихимическое. В условиях равновесия скорости процессов адсорбции и десорбции равны.

Константа адсорбционного равновесия

где к_адс – константа скорости адсорбции; к_дес – константа скорости десорбции.

Исходя из данной теории было выведено уравнение, которое мы приводим без вывода:

(3.15)

где – максимальная адсорбция ПАВ; Г – адсорбция при концентрации с; К – константа адсорбционного равновесия.

Зависимость величины адсорбции от концентрации представлена на рис.3.7.

На кривой четко видны три участка:

I участок – прямая линия, выходящая из начала координат. Действительно, из уравнения Ленгмюра (3.15) при малых концентрациях Кс > 1 и 1 + Кс Кс. Следовательно,

II участок – соответствует криволинейной части графика и описывается полным eравнением Ленгмюра (3.15).

Рис.3.7. Зависимость адсорбции от концентрации ПАВ.

Чтобы найти постоянные в уравнении Ленгмюра, его следует привести к линейной форме. Для этого правую и левую части уравнения надо «перевернуть»:

(3.16)

Умножим обе части уравнения (3.16) на с:

(3.16)

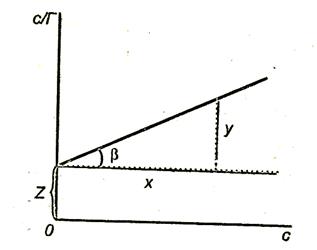
На рис. 3.8. показан график .

Тангенс угла наклона прямой к оси абсцисс

Отрезок, отсекаемый прямой на оси ординат,

Рис.3.8. Зависимость величины с/Г от концентрации ПАВ.

Доказано, что К в уравнении Шишковского (удельная капиллярная постоянная) и К в уравнении Ленгмюра (константа адсорбционного равновесия) – это одна и та же величина.

Построив график , можно найти предельную адсорбцию и константу адсорбционного равновесия К.

Так как адсорбция рассматривается как псевдохимическая реакция, на основе химической термодинамики можно записать

(3.18)

где А_m_ах – работа адсорбции.

Шишковский эмпирическим путем установил, что константа К увеличивается в 3–3,5 раза при удлинении цепи на одно звено –СН₂.

Напишем выражение для разности работ адсорбции двух соседних членов гомологического ряда.

= 8,31 * 298 * In 3,5 3,2 кДж/моль,

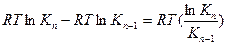
где n – число атомов углерода в углеводородном радикале.

Это означает, что для перевода каждой –СН₂–группы из поверхностного слоя в объемную фазу надо затратить 3,2 кДж/моль энергии. Это работа раздвижения диполей воды на величину объема –СН₂–группы – величина аддитивная и одинаковая для различных рядов алифатических предельных соединений. Постоянная разность работ адсорбции для двух соседних членов превращается в постоянное отношение (3–3,5), фигурирующее в правиле Дюкло–Траубе. Сущность этого правила, таким образом, заключается в том, что работа адсорбции на каждую –СН₂–группу является постоянной, близкой к 3,5 кДж/молъ.

В заключение отметим, что помимо уравнения Гиббса, Шишковского и Ленгмюра существует уравнение Фрумкина, позволяющее рассчитать изменение поверхностного натяжения в результате адсорбции:

(3.19)

ЗАКЛЮЧЕНИЕ

Адсорбция поверхностно-активных веществ (ПАВ) на поверхности «жидкий раствор–газ» – самопроизвольный процесс, обусловленный уменьшением поверхностного натяжения. Для поверхностно-инактивных веществ (ПИВ), повышающих поверхностное натяжение, характерна отрицательная адсорбция.

Основным уравнением адсорбции является уравнение Гиббса, связывающее величину избыточной адсорбции с концентрацией ПАВ и его поверхностной активностью. Кривая, выражающая зависимость поверхностного натяжения от концентрации ПАВ при постоянной температуре, называется изотермой поверхностного натяжения. Тангенс угла наклона к оси абсцисс касательной к изотерме поверхностного натяжения при с 0 позволяет определить поверхностную активность. Аналитическим выражением изотермы поверхностного натяжения является уравнение Шишковского, выведенное на основе экспериментальных данных. Если известны постоянные этого уравнения и поверхностное натяжение растворителя, можно рассчитать поверхностное натяжение раствора заданной концентрации.

Поверхностная активность ПАВ, согласно теории Ленгмюра, обусловлена дифильным строением их молекул: полярные группы втягиваются в глубь фазы, а неполярные углеводородные части выталкиваются в неполярную среду (воздух, газ), снижая тем самым поверхностное натяжение. С увеличением углеродной цепи на одну –СН₂–группу поверхностная активность увеличивается в 3-3,5 раза (правило Дюкло–Траубе). Исходя из теории Ленгмюра, были впервые рассчитаны площадь, занимаемая одной молекулой, и длина молекулы ПАВ.

Зависимость величины адсорбции ПАВ от концентрации выражается уравнением Ленгмюра, выведенным исходя из представлений о скоростях процессов адсорбции и десорбции. Соответствующий график Г = f(с) называется изотермой Ленгмюра.

Изменение поверхностного натяжения в зависимости от адсорбции рассчитываются по уравнению Фрумкина.

ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ

1. Какие вещества называются поверхностно-активными, поверхностно-инактивными?

2. В чем состоят особенности строения молекул ПАВ и ПИВ и их адсорбции?

3. Как зависит поверхностное натяжение от концентрации ПАВ в растворе?

4. Что называется поверхностной активностью? Как ее можно определить графически и аналитически?

5. В чем заключается правило Дюкло–Траубе?

6. Как графически и аналитически можно определить предельную адсорбцию?

7. Как рассчитать площадь, занимаемую молекулой, и толщину поверхностного слоя?

8. Для водных растворов изоамилового спирта константы уравнения Шишковского: В = 21,12 * 1СГ 3 Дж/м 2 ; К = 42,0 м 3 /кмоль. Поверхностное натяжение чистой воды при заданной температуре равно 72,9 * 10 -3 Дж/м 2 :

а) определите поверхностное натяжение растворов концентраций: 0,012; 0,016; … 0,032 кмоль/м 3 ,

б) постройте изотерму поверхностного натяжения,

в) определите графически поверхностную активность спирта,

г) по уравнению Гиббса вычислите адсорбцию спирта для заданных в п. а) концентраций,

д) постройте изотерму адсорбции и определите графи чески предельную адсорбцию,

е) определите площадь, занимаемую одной молекулой спирта в поверхностном слое.

9. Сравните поверхностную активность этанола и н-бутанола в водных растворах одинаковой концентрации.

10 Изотерма адсорбции ПАВ описывается уравнением Ленгмюра Г=Г_m_ах*(Кс/(1 + Кс)). Найдите графическим методом константы Г_m_ах и К.

11. Предельная адсорбция пропионовой кислоты равна 4,18 * 10 -6 моль/м 2 . Рассчитайте значение константы В в уравнении Шишковского, при стандартной температуре.

Закончив изучение главы 3, вы должны

1. понятия «поверхностно–активные» и «поверхностно-инактивные» вещества, «поверхностная активность»;

2. от чего зависит поверхностная активность ПАВ;

3. сущность теории мономолекулярной адсорбции Ленгмюра;

4. уравнения Гиббса, Шишковского, Ленгмюра, Фрумкина, какие зависимости каждое из них выражает;

1. строить изотерму поверхностного натяжения и определять графически поверхностную активность;

2. рассчитывать поверхностную активность по уравнению Гиббса;

3. рассчитывать поверхностное натяжение по уравнению Шишковского;

4. строить изотерму гиббсовской адсорбции и определять предельную адсорбцию ПАВ;

5. исходя из предельной адсорбции рассчитывать поперечный размер So и длину молекул .

Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Лекция 13. Адсорбция

13.1. Уравнение адсорбции Гиббса

Строгое определение понятия адсорбции по Дж. Гиббсу: адсорбцией данного компонента на границе раздела двух фаз называется разность между фактическим количеством этого компонента в системе и тем его количеством, которое было бы в системе, если бы концентрации в обеих сосуществующих фазах были постоянны вплоть до некоторой геометрической поверхности, разделяющей их.

Эта разность может быть положительной или отрицательной. Она обозначается символом G (гамма) и имеет размерность моль/м 2 . Эту величину называют избыточной адсорбцией по Дж. Гиббсу.

Хотя в приведенном определении адсорбция отнесена к геометрической поверхности, не имеющей толщины (что удобно при выводе уравнений), фактически граница между фазами представляет собой очень тонкий слой (поверхностный слой), в котором все свойства отличаются от свойств объемных фаз и изменяются не скачкообразно, а непрерывно.

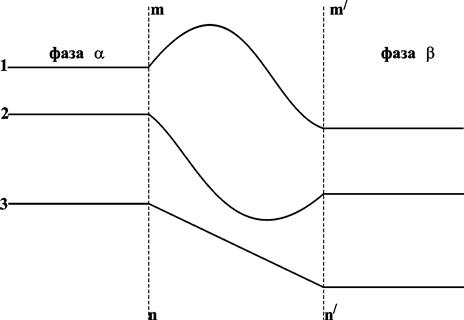
На рис. 13.1 показано возможное изменение концентрации вблизи границы раздела: концентрация компонента может быть как выше концентраций в обеих фазах (1), так и ниже (2) или иметь промежуточное значение. Эта область может рассматриваться как поверхностный слой. Таким образом, изучая границу раздела фаз, нужно рассматривать состояние трех фаз: двух объемных и одной поверхностной.

Рис. 13.1. Изменение концентрации компонентов у границы раздела фаз;
поверхностный слой – mn-m’n’

Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции – величиной поверхностного натяжения s, концентрацией компонента [C] в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Это уравнение является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.

Рассмотрим систему, состоящую из двух компонентов 1 и 2 и двух фаз a и b, разделенных поверхностью раздела с площадью S. Общее число молей каждого компонента в системе равно n₁ o и n₂ o . Если считать, что поверхностный слой не имеет толщины, т.е. представляет собой геометрическую поверхность, то обе объемные фазы будут иметь постоянный состав вплоть до этой геометрической поверхности. Обозначим число молей каждого компонента в каждой из этих фаз соответственно через n₁ a ,n₁ b ; n₂ a ,n₂ b . Так как на поверхности имеет место адсорбция, то, очевидно, n₁ o ¹ n₁ a + n₁ b и n₂ o ¹ n₂ a + n₂ b .

По вышеприведенному определению адсорбция каждого компонента Г₁ и Г₂ , отнесенная к единице площади поверхности, равна

. (13.1)

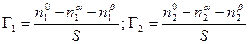
Чтобы найти Г₁ и Г₂, напишем уравнение энергии Гиббса для двух фаз a и b в отдельности и для всей системы в целом. В последнем случае, очевидно, нужно включить в уравнение член sdS:

dG o = — S o dT + V o dP + sdS + m₁dn₁ o + m₂dn₂ o . (13.2)

Укажем на уравнение Гиббса-Дюгема, которое устанавливает связь между химическими потенциалами:

dG = — S dT + VdP + Sm_idn₁ (P, T – постоянные). (13.3)

Тогда для бинарной системы получим

Интегрируя это уравнение при постоянных значениях m₁ и m₂, получим

Из (13.4) и (13.6) вытекает, что

. (13.7)

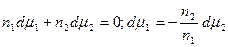
Это уравнение носит название уравнения Гиббса-Дюгема и связывает изменение химических потенциалов компонентов. Тогда с учетом уравнения Гиббса-Дюгема и поверхностных явлений получаем:

Сложение двух первых уравнений и вычитание полученной суммы из третьего дает

. (13.9)

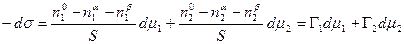
В качестве примера рассмотрим две конкретные системы: двухкомпонентный жидкий раствор, находящийся в равновесии со своим двухкомпонентным насыщенным паром, и твердое тело, находящееся в равновесии с однокомпонентным газом, совершенно не растворимым в этом твердом теле.

Поскольку в первом случае точное положение разделяющей геометрической поверхности несколько условно, то можно выбрать положение ее, при котором

Во втором случае вследствие нерастворимости газа в объеме твердого тела, объемные свойства этого тела, в частности его химический потенциал, не изменяются при адсорбции. Приписывая твердому телу индекс 1, имеем:

В обоих случаях получено одно и то же уравнение. Поэтому можно считать, что адсорбционное уравнение Гиббса имеет вид:

Оно является основным в учении о поверхностных явлениях.

Рассмотрим далее реальный раствор. Для реального раствора

где а – активность, тогда:

Подставив это значение в уравнение (13.12), получим:

ds = — Г Rt d lna,

. (13.13)

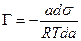
В разбавленных растворах а » С (где С – концентрация)

, (13.14)

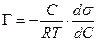
а для идеального или разреженного идеального газа

. (13.15)

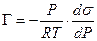
Уравнение (13.14) показывает, что если при адсорбции поверхностное натяжение s уменьшается с ростом концентрации С, т.е. ds/dC 0 и Г – отрицательно. Это соответствует поверхностно-инактивным веществам. Если известна зависимость s от С (т.е. изотерма поверхностного натяжения s = f(C) , то по уравнению Гиббса можно для каждого значения концентрации найти ds/dC и по уравнению Гиббса вычислить значение Г, т.е. построить изотерму адсорбции.

13.2. Обзор сорбционных явлений

Адсорбция на границе раздела твердое тело/газ. В общем случае явления, связанные с перераспределением веществ между различными частями гетерогенной системы, называются сорбцией. Сорбция (от лат. sorbeo – сгущать) – это изменение концентрации (часто увеличение) либо у поверхности раздела фаз (адсорбция), либо в объеме одной из фаз (абсорбция). Например, образование раствора за счет поглощения НСl (газа) и поглощение газа металлом (абсорбция). Поверхностная сорбция – адсорбция.

Твердое тело, у поверхности которого происходит адсорбция, называется адсорбентом, адсорбирующийся газ или адсорбирующийся компонент жидкого раствора – адсорбтивом, а адсорбированое вещество – адсорбат.

В строгом определении адсорбции она рассматривается как избыток вещества вблизи поверхности по сравнению с равным объемом вдали от нее. В ряде случаев удобнее рассматривать не избыток, а все количество адсорбата вблизи поверхности. Это количество обозначают символом а и называют полным содержанием, или просто адсорбцией (без указания гиббсова). Так как для пористых твердых тел бывает затруднительно знать величину поверхности, то часто адсорбцию относят не к единице поверхности, а к единице массы (моль/кг или моль/г).

Адсорбция самопроизвольна и протекает при Р = const со снижением энергии Гиббса, а при V = const – со снижением энергии Гельмгольца. Однако при этом происходит не выравнивание концентраций по всему объему системы, а увеличение разности концентраций между газовой фазой (раствором) и поверхностью. Одновременно уменьшается подвижность сорбирующихся молекул. Оба фактора ведут к уменьшению энтропии (DS o , так как DG o = DH o + TDS o ,

. (13.26)

. (13.27)

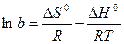
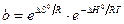
Таким образом, адсорбционный коэффициент b связан со стантартной энтропией DS° и со стандартной теплотой адсорбции q = –DH°.

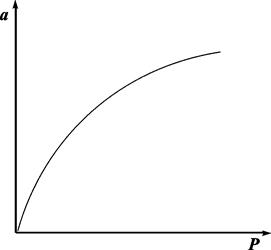
Очень часто а_m называют «емкость монослоя». На рис.13.3 показана кривая, выражающая изотерму адсорбции по Ленгмюру

Рис. 13.3. Изотерма адсорбции по Ленгмюру

При очень малых заполнениях и, следовательно, очень малых давлениях Р в знаменателе, согласно (13.25), bр > 1 и а = а_m, т.е. величина адсорбции перестает зависеть от давления, поскольку все центры уже заняты.

Для расчета параметров a_m и b уравнение Ленгмюра представляют в виде

. (13.28)

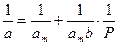
Тангенс угла наклона этой линии равен 1/a_mb, а отрезок, отсекаемый на оси ординат, равен 1/a_m.

Уравнение Ленгмюра, полученное на основании модели локализованной адсорбции газов на поверхности твердого тела, часто хорошо описывает адсорбцию растворенных веществ на поверхности жидкости (поверхность раздела раствор/газ), при которой адсорбция не локализована, так как молекулы подвижны и образуют двумерную газо- или жидкообразную пленку.

Обусловлено это тем, что основные положения модели Ленгмюра соблюдаются при адсорбции из растворов: поверхность жидкости идеально однородна, взаимодействие адсорбированных молекул в адсорбционном слое мало отличается от их взаимодействия в растворе. Оно к тому же ослаблено за счет взаимодействия молекул растворенного вещества с молекулами растворителя и практически не влияет на адсорбцию.

Уравнение Ленгмюра связано с уравнением состояния адсорбционной пленки – уравнением Гиббса. Так,

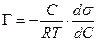
а по уравнению Ленгмюра

;

. (13.29)

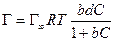
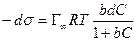
После интегрирования в пределах от s_о до s и от 0 до С получим:

, (13.30)

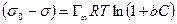
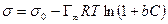
где Г_¥ связано с площадью, занимаемой 1 моль адсорбированного вещества в мономолекулярном слое, следующим соотношением: .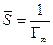

Дата добавления: 2016-02-09 ; просмотров: 2870 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Решение задач на вычисление энергии Гиббса. 1 часть. 10 класс.Скачать

1.7. Определение адсорбции ПАВ на поверхности водных растворов

Для расчетапараметров молекул в адсорбционном слое прежде всего необходимо провести определение адсорбции ПАВ на поверхности водного раствора. Для этого обычно используют один из двух методов, основанных на обработке изотермы поверхностного натяжения.

Поверхностное натяжение растворов ПАВ определяют одним из описанных выше методов. Полученные данных используют для построения изотермы поверхностного натяжения, пример которой показан на рис. 1.20.

Для расчета адсорбции используют уравнение (1.1.100) изотермы адсорбции Гиббса. Для этого находят поверхностную активность 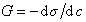в нескольких точках изотермы поверхностного натяжения.

Для нахождения G к заданным точкам кривой s= f(c) проводят касательные, как это показано на рис. 1.20, определяют тангенс угла наклона касательных, который равен ds/dc. По найденной поверхностной активности для разных концентраций рассчитывают по уравнению Гиббса адсорбцию (моль/м 2 ). Затем строят изотерму адсорбции в области возможно наименьших концентраций, так как уравнение изотермы Гиббса в форме уравнения 1.1.100 справедливо в области малых концентраций растворов. Для расчета максимальной адсорбции Г_max можно воспользоваться одним из двух вариантов линейной формы уравнения изотермы адсорбции Ленгмюра:

Если единицу поделить на левую и правую часть уравнения (1.1.113), то получаем уравнение

. (1.1.122 )

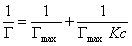
После построения изотермы адсорбции в координатах этого уравнения находят предел адсорбции Г_max как величину, обратную отрезку, отсекаемому на оси ординат. Этот метод обычно связан с высокой погрешностью определения Г_max, так как величина отрезка бывает небольшой. В этой связи часто прибегают к обработке экспериментальных данных по линейной форме изотермы адсорбции Ленгмюра, получающейся при делении равновесной концентрации раствора на левую и правую части уравнения (1.1.113). В этом случае получается уравнение

. ( 1.1.123)

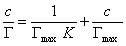
Линейная зависимость с/Г = f(с) отсекает на ординате отрезок, позволяющий найти 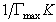, а тангенс угла наклона прямой к оси абсцисс равен 1/Г_m_ax_.

После нахождения предела адсорбции рассчитывают параметры молекул ПАВ в адсорбционном слое.

Определить предел адсорбции и постоянной равновесия адсорбцииможно такжеc помощью уравнения Шишковского (как описано выше, при обсуждении этого уравнения).

В табл. 1.1 приведены поверхностное натяжение некоторых жидкостей, их межфазовые натяжения на границе с водой при температуре 293,2 K, температурные коэффициенты поверхностного и межфазового натяжений, а также работа адгезии жидкости к воде.

органической жидкости в воде (W₁₂₃), температурный коэффициент