Работа расширения можно выразить в виде уравнения (8 видео)

Блог об энергетике

Содержание

энергетика простыми словами
Основные термодинамические процессы
Изохорный процесс
Изобарный процесс
Изотермический процесс
Адиабатный процесс
Политропный процесс
Первый закон термодинамики.
Применение первого закона термодинамики к различным процессам .
Изохорный процесс.
Первый закон термодинамики
Определение 1 -го закона термодинамики
Первый закон термодинамики в процессах газов
🔍 Видео

Видео:Адиабатный процесс. 10 класс.Скачать

энергетика простыми словами

Видео:Работа по расширениюСкачать

Основные термодинамические процессы

Основными процессами в термодинамике являются:

изохорный, протекающий при постоянном объеме;
изобарный, протекающий при постоянном давлении;
изотермический, происходящий при постоянной температуре;
адиабатный, при котором теплообмен с окружающей средой отсутствует;
политропный, удовлетворяющий уравнению pv n = const.

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

уравнение процесса в p—v иT—s координатах;
связь между параметрами состояния газа;
изменение внутренней энергии;
величину внешней работы;
количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.

Изохорный процесс

При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

т. е. давление газа прямо пропорционально его абсолютной температуре:

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Изменение энтропии в изохорном процессе определяется по формуле:

Изобарный процесс

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

Количество теплоты при c_p = const определяется по формуле:

Изменение энтропии будет равно:

Изотермический процесс

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

k_{выхлопных газов ДВС} = 1,33

Из предыдущих формул следует:

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

n > 0 – гиперболические кривые,

n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Первый закон термодинамики.

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Манером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

где ΔU — изменение внутренней энергии, A — работа внешних сил, Q — количество теплоты, переданной системе.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение (ΔU = A + Q) записывается в виде:

где A’ — работа, совершаемая системой (A’ = -A).

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника (т. е. только за счет внутренней энергии).

Действительно, если к телу не поступает теплота (Q — 0), то работа A’, согласно уравнению , совершается только за счет убыли внутренней энергии А’ = -ΔU. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.

Следует помнить, что как работа, так и количество теплоты, являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Применение первого закона термодинамики к различным процессам .

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Видео:Работа при расширении газа (часть 4) | Термодинамика | ФизикаСкачать

Изохорный процесс.

Зависимость р(Т) на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинамический процесс, происходящий в системе при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется (ΔV= 0), и, согласно первому началу термодинамики ,

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа (А = рΔV=0) газом не совершается.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Первый закон термодинамики

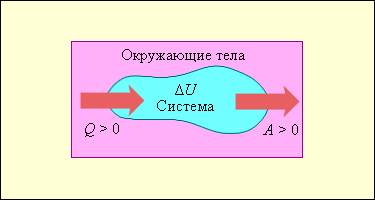
На рисунке 3 . 9 . 1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q > 0 , если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A > 0 .

Рисунок 3 . 9 . 1 . Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы Δ U .

Видео:Первый закон термодинамики. 10 класс.Скачать

Определение 1 -го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Видео:Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В изохорном процессе, то есть в условиях неизменного объема ( V = c o n s t ) , газ не совершает работы, A = 0 .

В этом случае справедливой будет формула внутренней энергии газа:

Q = ∆ U = U ( T 2 ) — U ( T 1 ) .

В данном выражении U ( T 1 ) и U ( T 2 ) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло ( Q > 0 ) , чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам ( Q 0 ) .

В изобарном процессе, предполагающем постоянность значения давления ( p = c o n s t ) , работа, совершаемая газом, выражается в виде соотношения:

A = p ( V 2 — V 1 ) = p ∆ V .

Первый закон термодинамики для изобарного процесса дает:

Q = U ( T 2 ) — U ( T 1 ) + p ( V 2 — V 1 ) = ∆ U + p ∆ V .

При изобарном расширении Q > 0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q 0 тепло переходит внешним телам. В таком случае A 0 . При изобарном сжатии уменьшаются температура газа T 2 T 1 и значение внутренней энергии Δ U 0 .

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0 .

Первый закон термодинамики для изотермического процесса выражается соотношением

Теплота Q , приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

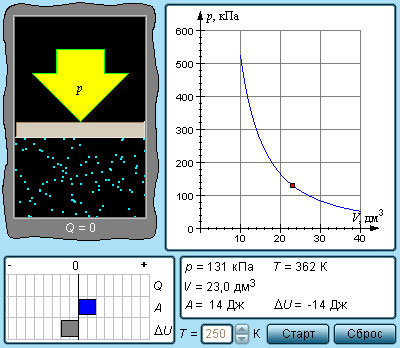
Рисунок 3 . 9 . 2 . Модель адиабатического процесса.

В адиабатическом процессе Q = 0 . По данной причине первый закон термодинамики принимает вид:

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Расширение или сжатие газа на плоскости p , V проиллюстрирована кривой, называемой адиабатой.

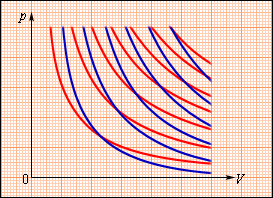
В процессе адиабатического расширения газом совершается положительная работа A > 0 , что является причиной понижения значения внутренней энергии Δ U 0 . Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3 . 9 . 3 ).

Рисунок 3 . 9 . 3 . Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат ( p , V ) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид:

p V γ = c o n s t .

Данное выражение, в котором γ = C p C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ = 5 3 = 1 , 67 , двухатомного γ = 7 5 = 1 , 4 , многоатомного γ = 1 , 33 .

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

A = C V ( T 2 — T 1 )

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу Δ Q T . Так как на каждом участке адиабатического процесса Δ Q = 0 , энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

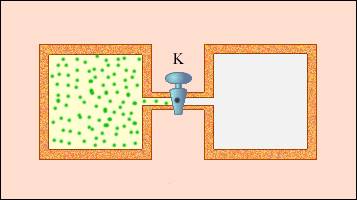
Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3 . 9 . 3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q = 0 , по той причине, что исключен теплообмен с окружающими телами, и A = 0 , так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что Δ U = 0 , то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости ( p , V ) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.