Расчёт каких аппаратов пожарной техники основан на уравнении Бернулли? Привести пример методики расчёта одного из указанных аппаратов.
На основе уравнения Бернулли рассчитаны следующие устройства: ствол-водомер (используется для измерения расхода воды, проходящей по рукавным линиям), водомер Вентури (является одним из устройств, предназначенных для измерения расхода жидкости в трубопроводах), трубка полного напора (приемник полного давления), позволяет измерить полный напор потока жидкости (она представляет собой трубку, изогнутую под прямым углом и направленную навстречу потоку).
Струйные аппараты так же нашли широкое применение в различных областях техники. Представляют собой устройство, которое позволяет подсасывать и поднимать на определенную высоту жидкость, порошок или другую рабочую среду. Достоинством струйных аппаратов является простота их устройства и безопасность в работе (но имеет низкий КПД). В пожарной технике наиболее широко используются водоструйные аппараты, в которых рабочей средой, подводимой к аппарату, является вода, а эжектируемой – порошок, пенообразователь. Принципиальное устройство водоструйного аппарата показано на рис. 25. Он состоит из следующих элементов: рабочего насадка 1, приемной камеры 2, камеры смешения 3, диффузора 4. Принцип действия аппарата заключается в следующем: рабочая жидкость с расходом воды Q1 проходит через насадок, на выходе из которого в результате увеличения скорости давление падает и в приемной камере образуется разряжение, за счет которого создается подсасываемый поток Q2.
Максимальное разряжение наблюдается на входе в камеру смешения. В диффузоре давление увеличивается. Струйный аппарат рассчитывается с использованием уравнений Бернулли для сечений 1-1 и 2-2, 3-3 и 4-4, 5-5 и 6-6.
Рис. 25. Схема водоструйного аппарата и примерное распределение давления по его длине.
Для сечений 1-1 и 2-2 уравнение Бернулли запишется:
В сечении 1-1 давление всегда избыточное, а в сечении 2-2- вакуум. Тогда с учетом уравнения неразрывности потока жидкости соотношение запишется:
Аналогичные соотношения получаются при использовании уравнения Бернулли для других сечений. Такая система уравнений позволяет связать между собой рабочие и геометрические параметры инжектора: расходы, давления и диаметры.
2. Сущность метода анализа размерностей. Вид формул для определения линейных и местных потерь напора. От каких величин зависят коэффициенты линейных (λ) и местных (ζ) потерь напора.
Метод теории размерностей широко применяется во многих исследованиях. Данный метод известен под названием «π – теорема. Согласно этой теореме, всякое уравнение, выражающее некоторую физическую закономерность и поэтому не зависящее от выбора системы единиц измерения, связывающее между собой k физических величин, среди которых n величин обладают независимыми размерностями, может быть преобразовано в уравнение, связывающее k-n независимых безразмерных комплексов, составленных из упомянутых k физических величин.
При движении жидкости по трубам могут возникать два вида потерь напора: по длине (линейные) потока и местные. Сопротивления (потери) по длине потока возникают в результате трения о стенки трубопровода и трения между слоями жидкости. Потери напора на трение по длине l определяются общей формулой Дарси:
где λ — безразмерный коэффициент сопротивления, определяется в зависимости от режима движения жидкости;
υ — средняя скорость потока.
Таблица для определения коэффициента гидравлического трения
Режим движения Число Рейнольдса Определение λ
Ламинарный Re 560 (ф-ла Шифринсона)
(ф-ла Никурадзе)
Местные потери напора происходят в местах изменения формы и размеров трубы, где происходит деформация потока — расширение, сужение, искривление и т.п. Местные потери выражают формулой Вейсбаха:
где υ — средняя скорость потока в сечении перед местным сопротивлением (при расширении) или за ним (при сужении);
ζм — безразмерный коэффициент местного сопротивления (зависит от вида местного сопротивления и диаметра трубопровода). Для определения коэффициента местного сопротивления можно использовать как формулы, так и справочные таблицы, например: при внезапном сужении трубы без закругления коэффициент сопротивления
– определяют по формуле Идельчика:
где ω1 и ω2 — площади сечений трубы до и после сужения.
– или выбирают из справочника
Литература
Гидравлика: Методические указания и варианты контрольной работы для слушателей заочного обучения. – Екатеринбург: УрИ ГПС МЧС России, 2011. – 30 с
Альтшуль А.Д, Киселев П.Г. Гидравлика и аэродинамика (Основы механики жидкости). Учебное пособие длявузов. Изд. 2-е, перераб. и доп. М., Стройиздат, 1975, 323 стр.
Гидравлика. / Под ред. Абросимова Ю.Г. – М.: АГПС МЧС России, 2005 г. – 312 с.
Задачник по гидравлике и противопожарному водоснабжению. / Под ред. Качалова А.А. Часть I. Гидравлика в пожарном деле. – М.: ВИПТШ МВД СССР, 1989 г. – 116 с.
Видео:Закон БернуллиСкачать

Практическое применение уравнения Бернулли
Уравнение Бернулли имеет широкое применение во многих гидравлических расчетах и для объяснения многих гидравлических явлений. В частности, оно может быть использовано при измерении давления и скорости движущейся жидкости. Для измерения давления используется пьезометр (прямая трубка на рис. 4.31). Для измерения скорости совместно с пьезометром используется трубка Пито – трубка полного напора. Она представляет собой трубку, изогнутую под прямым углом и установленную навстречу потоку.
Рис. 4.31. Схема определения скорости течения жидкости с помощью пьезометра и трубки Пито
Уровень жидкости в пьезометре равен
Разность уровней в пьезометре и в трубке полного напора будет равна скоростному напору
Действительно, запишем уравнение Бернулли для точек А и В:
Так как 





За счет вязкости жидкости и других отклонений от идеального случая преобразования энергии обычно 

Видео:Парадокс сужающейся трубыСкачать

Трубка Пито – Прандтля
Дальнейшим усовершенствованием трубки Пито является трубка Пито – Прандтля. В этом приборе объединяются трубка Пито и пьезометр (рис. 4.32). Роль трубки Пито здесь выполняет трубка 2 (она направлена навстречу потоку), а пьезометра – трубка 1 (отверстия в этой трубке находятся параллельно направлению потока).
Рис. 4.32. Трубка Пиго – Прандтля
Пусть в сечении I имеем давление и скорость набегающего потока р и и. В сечении II давление на входе в трубку 2 равно




Для определения

Применяя эту формулу для точек А и D, получаем
где

Так как при равновесии давление в точках А и D одинаково, то
Учитывая, что 
Подставляя последнее соотношение в формулу (4.25), находим
Для каждой отдельной трубки вводится некоторый коэффициент
Видео:Закон БернуллиСкачать

Трубка Вентури, сопло, диафрагма
В промышленных условиях для измерения расхода жидкостей применяются трубки Вентури, сопла и диафрагмы. Более подробно рассмотрим трубку Вентури (рис. 4.33). Трубка Вентури создаст в трубопроводе местное сужение потока и по возникающему перепаду давлений Δр можно определить расход жидкости.
Для сечений I и II запишем уравнение Бернулли (считая распределение скоростей равномерным)
где 



Отсюда
Подставляя



Рис. 4.33. Трубка Вентури
Рис. 4.34. Схема распределения скоростей и давлений в трубке Вентури с дифференциальным трубным манометром
Объемный расход будет определяться по формуле

где С – величина, постоянная для данного расходомера (трубки Вентури).
Довольно часто вместо пьезометров для измерения перепада давления в расходомере применяют дифференциальный трубный манометр (рис. 4.34).
Учитывая, что над ртутью в трубках находится одна и та же жидкость плотностью ρ, можно записать

Значения Δh, полученные по формуле (4.27), можно использовать для определения расхода по формуле (4.26).
Аналогично для измерения расхода могут быть использованы диафрагмы (рис. 4.35) и сопла (рис. 4.36).
Рис. 4.35. Диафрагма
Рис. 4.35. Сопло
Видео:15. Основы теплотехники. Струйные аппараты. Эжектирование газов. Эжектор и инжектор.Скачать

Применение в технике уравнения Бернулли
Уравнение Бернулли широко применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов, насосов и т.п. На его основании сконструирован ряд приборов и устройств, таких как расходомер Вентури, карбюратор, водоструйный насос (эжектор), трубка Пито и т.д.
Измерение скорости потока и расхода жидкости
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.2.10), загнутый конец которой направлен навстречу потоку.
Трубка полного напора, или трубка Пито , служит для измерения скорости потока, например в трубе. Если установить в одном сечении потока трубку, изогнутую под углом 90, отверстием навстречу потоку и пьезометр, то жидкость в трубке поднимется над уровнем жидкости в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, следовательно, давление увеличивается на величину скоростного напора. Измерив, разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке.
Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
где Н — столб жидкости в трубке Пито.
Рис. 2.10 Трубка Пито и pасходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.2.10). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока – дросселирование. Расходомер состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в сужающемся месте возрастает, а давление падает. Возникает разность (перепад) давлений, которую можно измерить двумя пьезометрами или дифференциальным U-образным ртутным манометром.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:
Используя уравнение неразрывности
сделаем замену в получено выражении:
Решая относительно Q, получим
Выражение, стоящее перед 

Карбюратор поршневых двигателей внутреннего сгорания (рис.2.11) служит для подсоса бензина и смешивания его с потоком воздуха. Поток воздуха, засасываемого в двигатель, сужается в том месте (сечение 2-2), где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.
Рис. 2.11. Схема карбюратора
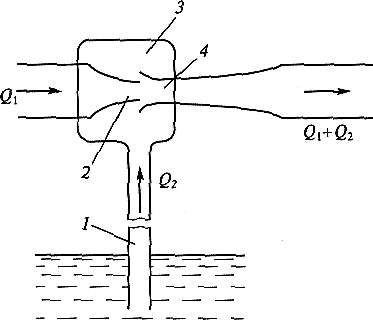
Рис. 2.12. Схема струйного насоса (эжектора):
1 — труба; 2 — насадок; 3 — камера; 4 — расширяющаяся трубка
🔥 Видео
Гидродинамика. Вторая лекция.Скачать

Как работают системы пожаротушения | InfoResistСкачать

Испытание системы пожаротушения сработка спринклераСкачать

Уравнение БернуллиСкачать

Пожарная тактика. Как рассчитать расход из любого пожарного ствола при любом напореСкачать

Принцип автоматической системы пожаротушения.Скачать

Гидравлический расчет водяного пожаротушенияСкачать
Принцип работы автоматической пожарной сигнализации. Обучение пожарной безопасности [2019]Скачать
![Принцип работы автоматической пожарной сигнализации. Обучение пожарной безопасности [2019]](https://i.ytimg.com/vi/lyYBosnIV0U/0.jpg)
Гидравлика и гидрология (лекция 2)Скачать

Тема 11. Работа в термодинамике. Решение задач по теме «Работа в термодинамике»Скачать

Безопасное ведение огневых работ на опасных производственных объектахСкачать

Дымовые пожарные датчики (подключение, устройство, принцип работы)Скачать

ГраФиС-Тактик. Работа с совмещенным графикомСкачать

Видеоурок по химии "Знакомство с лабораторным оборудованием. Правила техники безопасности"Скачать

Особенности тушения пожара на электроустановкахСкачать

Огнетушащие вещества и принципы тушения пожаровСкачать



























