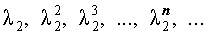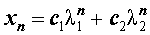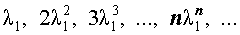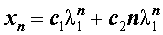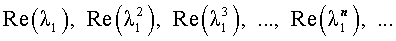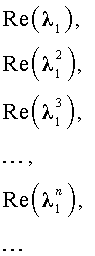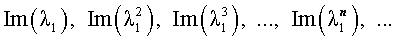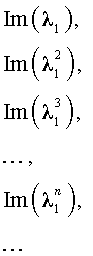В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
- Как решать рекуррентные соотношения?
- Метод производящих функций
- Метод характеристических функций
- Решение для последовательности чисел Фибоначчи
- Способ 1. Производящяя функция
- Способ 2. Характеристическое уравнение
- Примеры решений
- Возвратные последовательности: рекуррентная формула, характеристическое уравнение
- Определение возвратной последовательности
- Характеристическое уравнение
- Общее решение рекуррентного уравнения второго порядка
- РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Разностное уравнение и рекуррентная последовательность
- Линейное уравнение
- Идея решения
- Аналитика
- Метод производящего ряда
- Метод матричной степени
- Cистемы линейных разностных уравнений
- Асимптотика
- Метод конечных разностей
- Поиск корня полинома методом Бернулли
- Алгоритм «деления-вычитания» вычисления корней полинома
- Задачи
- Источники
- 🎥 Видео
Видео:Что такое математическая последовательность? | Математика | TutorOnlineСкачать

Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
- Метод производящих функций
- Метод характеристического уравнения
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
- Записать рекуррентное соотношение и начальные данные для него в следующем виде (если порядок соотношения равен $k$) $$a_ = …, \ a_ = …, \ a_ = …, \ … \ a_ = …, ngeqslant k$$
- Домножить каждую строчку на $z$ в соответствующей степени $z^ cdot a_$ и сложить все выражения для $n ge 0$. В левой части получится сумма $displaystylesum_^ a_nz^n$ — это производящая функция, назовем ее $G(z)$. Правую часть преобразовать так, чтобы она превратилась в выражение, включающее $G(z)$.
- Решить полученное уравнение относительно $G(z)$.
- Разложить $G(z)$ в степенной ряд, тогда коэффициент при $z_n$ будет искомым выражением для $a_n$.
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
- Записать соответствующее однородное рекуррентное уравнение (РУ): $$ p_ a_ + p_a_ + . + p_n a_n =f to \ to p_ a_ + p_a_ + . + p_n a_n =0. $$
- Выписать для него характеристическое уравнение и найти его корни $lambda_i$ $$ p_ lambda^ + p_lambda^ + . + p_lambda + p_n =0. $$
- Выписать согласно полученным корням $lambda_1, . lambda_k$ общее решение однородного рекуррентного соотношения (подробнее теорию см. по ссылке [1] ниже). $$ C_1 lambda_1^n +. +C_k lambda_k^n , mbox , $$ $$ C_1 lambda_1^n + C_2 nlambda_1^n +. +C_m n^m lambda_1^n+. +C_k lambda_k^n mbox , lambda_1 , , m. $$
- Подобрать частное решение неоднородного рекуррентного соотношения по виду правой части (особенно удобно для правых частей вида $mu^n*P(n)$, $P(n)$ — многочлен от $n$).
- Представить общее решение неоднородного РУ как сумму общего решения соответствующего однородного РУ и частного решения неоднородного РУ.
- Подставить начальные условия $a_0, a_1, . a_$ и получить значения констант $C_1, . C_k$.
Видео:Предел числовой последовательности. 10 класс.Скачать
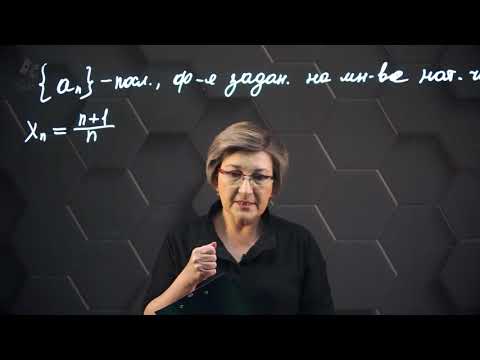
Решение для последовательности чисел Фибоначчи
Последовательность чисел Фибоначи — это последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:
$$ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , . $$
Числа Фибоначчи растут быстро: $f_=55$, $f_=6765$, а $f_=354224848179261915075$.
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
Начинаем с второго шага алгоритма, домножаем на $z^n$:
$$begin 1cdot f_0 &= &0cdot 1,\ zcdot f_1 &= &1cdot z,\ zcdot f_n & = &(f_+f_)cdot z^n, quad ngeq2.\ end $$
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на $z_1$:
Аналогично (но с делением на $z_2$) действуем со второй дробью:
Преобразуем данное выражение, используя то, что
$$1/z_1=-z_2, quad 1/z_2 = -z_1, quad z_1-z_2=sqrt $$ $$f_n=frac<sqrt>left( biggl( frac<1+sqrt> biggr)^n — biggl( frac<1-sqrt> biggr)^n right). $$
Способ 2. Характеристическое уравнение
Запишем характеристический многочлен для $f_n=f_+f_$, и найдем его корни:
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Осталось найти значения произвольных постоянных $C_1, C_2$ из начальных условий $f_0=0, f_1=1$.
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Видео:Последовательности. Алгебра, 9 классСкачать

Примеры решений
Задача 1. Решить рекуррентное соотношение $f(n+2)=-6f(n+1)+7f(n)+n-3$ с начальными условиями $f(0)=2$ и $f(1)=4$, сделать проверку
Задача 2. Решить рекуррентное соотношение $f(n+2)=-2f(n+1)+3f(n)-3^n$ с начальными условиями $f(0)=1$, $f(1)=3$ и сделать проверку
Задача 3. 1. Решить рекуррентное соотношение $f(n+2) =-5f(n+1) -4f(n) + 3n^2$ с начальными условиями $f(0) = 2$, $f(1) = 3$.
2. Проверить, удовлетворяет ли найденное решение начальным условиям и обращает ли оно рекуррентное соотношение в справедливое тождество.
Задача 4. Найти последовательность $$, удовлетворяющую рекуррентному соотношению $a_ + 4 a_ + 3 a_ = 0$ и начальным условиям $a_1=2$, $a_2=4$.
Видео:Понятие числовой последовательности. 9 класс.Скачать

Возвратные последовательности:
рекуррентная формула, характеристическое уравнение
 Определение возвратной последовательности Определение возвратной последовательности |
 Характеристическое уравнение Характеристическое уравнение |
 Общее решение рекуррентного уравнения 2-го порядка Общее решение рекуррентного уравнения 2-го порядка |
 Схема вывода формулы общего члена возвратной последовательности второго порядка Схема вывода формулы общего члена возвратной последовательности второго порядка |
 Примеры с решениями Примеры с решениями |
Видео:Понятие числовой последовательности. Практическая часть. 1 часть. 9 класс.Скачать

Определение возвратной последовательности
в каждой из которых символами b1 и q обозначены заданные числа – первый член и знаменатель прогрессии.
Определение . Пусть k – натуральное число. Возвратной (рекуррентной) последовательностью порядка k называют последовательность, для задания которой требуется задать первые её k членов, т.е. числа
а остальные члены последовательности определяются с помощью рекуррентной формулы (рекуррентного уравнения)
– заданные числа ( коэффициенты рекуррентной формулы ).
Замечание 1 . Числа
называют начальными условиями .
Замечание 2 . Для упрощения вычислений везде в дальнейшем будем рассматривать только случай возвратных последовательностей 2-го порядка, все члены которых являются вещественными числами.
Для задания таких последовательностей требуется задать их первые два члена, то есть вещественные числа x1 и x2 , а остальные члены последовательности
| xn = q1 xn – 1 + q2 xn – 2 , n > 2 , | (1) |
Видео:3. Пример 1 на доказательство предела числовой последовательностиСкачать

Характеристическое уравнение
Для того, чтобы получить характеристическое уравнение возвратной последовательности (1), будем искать такие числа λ , при которых последовательность вида
| xn = λ n | (2) |
удовлетворяет рекуррентной формуле (1).
| xn – 1 = λ n – 1 , xn – 2 = λ n – 2 , | (3) |
то при подстановке формул (2) и (3) в формулу (1) возникает уравнение
которое удобно переписать в виде
| λ n – q1 λ n – 1 – – q2 λ n – 2 = 0 . | (4) |
Если теперь уравнение (4) разделить на λ n–2 , то мы получим квадратное уравнение относительно λ вида:
которое и называют характеристическим уравнением .
Видео:Математика Без Ху!ни. Предел последовательности.Скачать

Общее решение рекуррентного уравнения второго порядка
В случае, когда характеристическое уравнение имеет два различных вещественных корня λ1 и λ2 , каждая из последовательностей
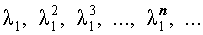
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Числа c1 и c2 называют произвольными постоянными .
В случае, когда характеристическое уравнение имеет два совпавших вещественных корня λ1 = λ2 , непосредственная проверка показывает, что каждая из последовательностей
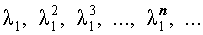
и
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
В случае, когда характеристическое уравнение имеет два комплексно-сопряженных корня λ1, 2 = α ± i β, каждая из последовательностей
удовлетворяет рекуррентной формуле (1), поэтому для любых чисел c1 и c2 последовательность с общим членом
также удовлетворяет рекуррентной формуле (1).
Ряд примеров, в которых выводятся формулы общего члена возвратных последовательностей, разобран в разделе «Возвратные последовательности: вывод формулы общего члена» нашего справочника.
Видео:27. Вычисление предела функции №1. Примеры 1-4Скачать

РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ
1 РЕШЕНИЕ РЕКУРРЕНТНЫХ УРАВНЕНИЙ Обозначим через значение некоторого выражения при подстановке в него целого числа Тогда зависимость члена последовательности от членов последовательности F F со значениями аргумента меньшими называется рекуррентным уравнением Примером может служить уравнение вида: F Рекуррентное уравнение имеет порядок если оно позволяет выразить член последовательности F через члены F F Таким образом уравнение имеет порядок а уравнение F 3 6 имеет порядок 3 Если задано рекуррентное уравнение -го порядка то ему удовлетворяет бесконечно много последовательностей Но если первые элементов заданы то все остальные определяются однозначно А именно элемент выражается через элемент F через элементы F и тд Алгоритм решения рекуррентного уравнения приведен на Рис Отметим что уравнение описывает так называемую последовательность чисел Фибоначчи: 3 F 4 3 F 5 5 F F 8 Фактически алгоритм решения сводится к тому что на каждом шаге пользуясь начальными членами и заданным уравнением мы вычисляем очередной член последовательности Действуя таким образом мы рано или поздно получим любой член последовательности Однако при этом нам придется вычислять и все предыдущие члены Во многих случаях удобнее иметь явную формулу для -го члена последовательности Будем говорить что некоторая последовательность является решением рекуррентного уравнения если при подстановке ее в уравнение последнее обращается в тождество Например последовательность 4 8 является одним из решений рекуррентного уравнения 3 Действительно общий член этой последовательности имеет вид Но при любом имеет место тождество Значит 3 Таким образом является решением рекуррентного уравнения Решение рекуррентного уравнения называется общим если оно зависит от произвольных постоянных C C и путем подбора этих постоянных можно получить любое решение данного уравнения Например для уравнения 5 6 общим решением будет F C C 3 3 Легко проверить что последовательность 3 обращает в тождество Поэтому достаточно показать что любое решение можно представить в виде 3 Но любое
2 решение однозначно определяется значениями и Поэтому надо показать что для любых чисел и найдутся такие и C что F C C 3C C 3 C Определитель системы равен При любых и система имеет решение Поэтому 3 действительно является решением F; F; I: FFF; FF; FF; F Рис Алгоритм формирования последовательности чисел Фибоначчи
3 ЛИНЕЙНЫЕ РЕКУРРЕНТНЫЕ УРАВНЕНИЯ Для решения произвольных рекуррентных уравнений общих правил не существует Однако есть весьма часто встречающийся класс уравнений решаемый единообразным методом Это рекуррентные уравнения вида f 4 где — некоторые числа постоянные коэффициенты а f — некоторая функция от Такие уравнения называются линейными потому что элементы последовательности F связаны линейной зависимостью Если при этом функция f то уравнения такого вида называются однородными или однородными уравнениями с постоянными коэффициентами В противном случае уравнения называются неоднородными ЛИНЕЙНЫЕ ОДНОРОДНЫЕ РЕКУРРЕНТНЫЕ УРАВНЕНИЯ Линейные однородные рекуррентные уравнения с постоянными коэффициентами имеют вид F 5 где — некоторые числа Очевидно что последовательность всегда будет решением любого однородного уравнения Такое решение называется тривиальным решением Сначала рассмотрим как решаются такие уравнения при то есть изучим уравнения вида F 6 Решение этих уравнений основывается на следующих двух утверждениях: Если F и F являются решениями рекуррентного уравнения 6 то при любых числах A и B последовательность F AF BF также является решением этого уравнения Действительно по условию F F F F Умножим эти равенства на тождества В результате получим: A и F F B соответственно и сложим полученные [ AF BF ] [ AF BF ] AF BF А это означает что F AF BF является решением уравнения 6 Если число является корнем уравнения
4 то последовательность является решением рекуррентного уравнения F Докажем это утверждение Пусть то и Подставляя эти значения в 6 получаем равенство или Оно справедливо так как по условию При имеем тривиальное решение любая последовательность вида где Заметим что наряду с последовательностью также является решением уравнения 6 Для доказательства этого факта достаточно использовать утверждение положив в нем A B Из утверждений и вытекает следующее правило решения линейных однородных рекуррентных уравнений второго порядка Пусть дано рекуррентное уравнение 6 F Составим квадратное уравнение 7 которое называется характеристическим уравнением данного рекуррентного уравнения Если это уравнение имеет два различных корня и то общее решение уравнения 6 имеет вид C C Докажем это утверждение Заметим сначала что согласно утверждению последовательности и являются решениями данного рекуррентного F F уравнения А тогда по утверждению и C C является его решением Надо только показать что любое решение уравнения 6 можно записать в этом виде Но любое решение уравнения второго порядка определяется значениями и Поэтому достаточно показать что система уравнений C C C C имеет решение при любых и Очевидно что этими решениями являются При C F C система всегда имеет решение Рассмотрим пример Как уже было сказано последовательность чисел Фибоначчи 3583 можно получить с помощью рекуррентного уравнения F 8 Для него характеристическое уравнение имеет вид Корнями этого квадратного уравнения являются числа
5 5 5 и Поэтому общее решение уравнения Фибоначчи имеет вид 5 5 C C 9 Начальными условиями являются значения F F В соответствии с этими начальными условиями получаем для и C систему уравнений C C C 5 C C Решая эту систему уравнений находим что C C и поэтому F 5 Таким образом это выражение при всех натуральных значениях принимает целые значения СЛУЧАЙ РАВНЫХ КОРНЕЙ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ Рассмотрим случай когда корни характеристического уравнения совпадают: В этом случае выражение C C уже не будет являться общим решением Ведь из-за того что это решение можно записать в виде C C C В результате остается только одна константа C и выбрать ее так чтобы уравнение удовлетворяло двум начальным условиям и вообще говоря невозможно Следовательно необходимо найти какое-нибудь другое решение отличное от Таким решением является В самом деле если квадратное F уравнение имеет два совпадающих корня то по теореме Виета а Поэтому уравнение записывается следующим образом: А тогда рекуррентное уравнение имеет вид Проверим что F тождество F F действительно является его решением Подставляя значения F в уравнение получим очевидное Значит — это решение нашего рекуррентного уравнения Таким образом нам известно уже два решения данного рекуррентного уравнения: и Тогда общее решение можно записать следующим образом: F F C C C C Теперь коэффициенты Cи C можно подобрать так чтобы выполнялись любые два начальные условия для F
6 C C C C Линейные рекуррентные уравнения порядок которых больше двух решаются таким же способом Пусть уравнение имеет вид F Составим характеристическое уравнение Если все корни этого алгебраического уравнения -й степени различны то общее решение уравнения имеет вид F C C C Если же например то этому корню соответствуют решения F F F3 F рекуррентного уравнения В общем решении этому корню соответствует часть C C C Составляя такие выражения для всех корней и складывая их получаем общее решение уравнения s P где — кратность корня s — число различных корней P — полином степени относительно Пример Рассмотрим уравнение F 4 Составим характеристическое уравнение Общее решение рекуррентного уравнения имеет вид C C C C Составляем систему уравнений для нахождения и C : C C C C 4 Решая систему получаем что C и C Таким образом решение рекуррентного уравнения имеет вид
7 ПОИСК КОРНЕЙ МНОГОЧЛЕНА При отыскании корней характеристического уравнения довольно часто приходится решать уравнения степени больше Для решения этой задачи можно использовать метод подбора те брать наугад число и проверять является ли оно корнем данного многочлена При этом можно довольно быстро натолкнуться на корень а можно и никогда его не найти Ведь проверить все числа невозможно так как их бесконечно много Другое дело если бы нам удалось сузить область поиска например знать что искомые корни находятся например среди тридцати указанных чисел А для тридцати чисел можно сделать проверку А в связи с этим важным представляется утверждение Теорема Если несократимая дробь / целые числа является корнем многочлена F x с целыми коэффициентами то старший коэффициент этого многочлена делится на а свободный член на В самом деле если x x x x где — целые числа и / является его корнем то F / те / / / Умножим обе части равенства на получим Отсюда следует что Очевидно что целое число делится на Но / — несократимая дробь те числа и взаимно просты а тогда как известно из теории делимости целых чисел числа и тоже взаимно просты Итак делится на и взаимно просто с значит делится на Аналогично доказывается что делится на Доказанная теорема позволяет значительно сузить область поиска рациональных корней многочлена с целыми коэффициентами Продемонстрируем это на конкретном примере Найдем рациональные корни многочлена 4 3 F x 6x 3x 4x 8x 8 Согласно доказанной теореме рациональные корни этого многочлена находятся среди несократимых дробей вида / где — делитель свободного члена 8 а — делитель старшего коэффициента 6 4 При этом если дробь отрицательная то знак — будем относить к ее числителю Например Значит можно сказать что делитель числа 8 а — положительный делитель числа 6 Так как делители числа 8 это ± 48 а положительными делителями числа 6 будут 36 то рациональные корни рассматриваемого многочлена находятся среди чисел ± / / 3/ 6 / 344 / 388/ 3 Напомним что мы выписали только несократимые дроби Таким образом мы имеем двадцать чисел-«кандидатов» в корни Осталось только проверить каждое из них и отобрать те которые действительно являются корнями Но опять-таки придется сделать довольно много проверок Следующая теорема упрощает эту работу
8 Теорема Если несократимая дробь / является корнем многочлена F x с целыми коэффициентами то F делится на для любого целого числа при условии что Для доказательства этой теоремы разделим F x на x с остатком Получим F x x s x Так как x — многочлен с целыми коэффициентами то таким же является и s x а — целое число Пусть s x b x b x b x b Тогда x x b x b x b x b Положим в этом равенстве x / Учитывая что F / получаем / b b b b Умножим обе части последнего равенства на : b b b b Отсюда следует что целое число делится на Но так как и взаимно просты то и тоже взаимно просты а значит F делится на Теорема доказана Вернемся теперь к нашему примеру и воспользовавшись данной теоремой еще больше сузим круг поиска рациональных корней Применим теорему для значений и те если несократимая дробь является корнем многочлена x то делится на а F делится на Очевидно что в нашем случае F 5 а 5 Заметим что заодно мы исключили из рассмотрения единицу Итак рациональные корни нашего многочлена следует искать среди чисел / / 3 / 6 / / 3 8 8/3 Рассмотрим / / Тогда и F 5 делится на это число Далее 3 и 5 также делится на 3 Значит дробь / остается в числе кандидатов в корни Пусть теперь / / В этом случае 3 и F 5 не делится на -3 Значит дробь / не может быть корнем данного многочлена Выполнив проверку для каждой из выписанных выше дробей получим что искомые корни находятся среди чисел / / 3 4 Таким образом с помощью довольно простого приема удалось значительно сузить область поиска рациональных корней рассматриваемого многочлена Проверив 4 3 оставшиеся кандидаты убедимся что многочлен x 6x 3x 4x 8x 8 имеет два рациональных корня / и / 3 Описанный выше метод позволяет находить лишь рациональные корни многочлена с целыми коэффициентами Между тем многочлен может иметь и иррациональные корни Так например рассмотренный в примере многочлен имеет еще два корня: ± 5 это корни многочлена x x 4 Заметим что при испытании кандидатов в корни с помощью последней теоремы обычно рассматривают случай ± Другими словами если / — кандидат в корни то проверяют делятся ли и F на и соответственно Но может случиться так что например те единица — корень а тогда делится на любое число и наша проверка теряет смысл В этом случае следует разделить x на x те получить x x s x и производить испытания для многочлена sx При этом не следует забывать что один корень x корень x уже найден
9 В некоторых случаях когда характеристическое уравнение относится к уравнениям специального вида его корни могут быть найдены с помощью подстановки К таким уравнениям относятся например симметрические и возвратные уравнения Симметрическим называется уравнение степени — четное вида x bx cx cx bx 3 Симметрические уравнения являются частным случаем возвратных К возвратным относятся уравнения вида x bx cx / c x / / b x где — некоторый коэффициент Рассмотрим например решение симметрических и возвратных уравнений четвертой степени Пусть дано симметрическое уравнение 4 x 3 bx cx bx Сначала понизим его степень разделив обе части на x Получим уравнение x bx c b / x / x 4 Произведем следующую подстановку: t x / x 5 Тогда учитывая что t x / x выражение 4 можно записать как t bt c 6 Решив уравнение 6 как обычное квадратное уравнение получим два корня t и t Теперь подставляя поочередно корни t и t в уравнение 5 получим два квадратных уравнения x tx x t x 7 Решение уравнений 7 дает нам все четыре корня исходного уравнения 3 Таким образом решение симметрического уравнения четвертой степени сводится к решению трех квадратных уравнений Аналогично решаются и возвратные уравнения Если уравнение четвертой степени можно представить в виде 4 x 3 bx cx bx 8 то его решение может быть получено с помощью подстановки t x / x 9 Также как и в предыдущем случае понизим степень уравнения поделив обе части на x Для получившегося уравнения x bx c b / x / x воспользуемся подстановкой 9 Тогда уравнение можно переписать в виде t bt c Так же как и в предыдущем примере решим уравнение и получим два корня t и t Теперь подставляя поочередно корни t и t в уравнение 9 получим два квадратных уравнения x tx x t x Решив систему уравнений получим четыре корня исходного уравнения 8 Таким образом решение возвратного уравнения четвертой степени также сводится к решению трех квадратных уравнений
10 РЕШЕНИЕ НЕОДНОРОДНЫХ ЛИНЕЙНЫХ РЕКУРРЕНТНЫХ УРАВНЕНИЙ Линейное рекуррентное уравнение называется неоднородным если его можно представить в следующем виде: f 3 где f — некоторая функция от Введем однородное линейное рекуррентное уравнение ОЛРУ соответствующее неоднородному линейному рекуррентному уравнению НЛРУ 3 F 4 а его общее решение обозначим через FO По аналогии с методами решения дифференциальных уравнений вначале пренебрежем начальными условиями и предположим что одно решение уравнения 3 уже найдено Назовем это решение частным и обозначим его через Будем искать общее решение НЛРУ в виде суммы F его частного решения и общего решения соответствующего ему ОЛРУ F 5 3 O Покажем что 5 действительно является решением НЛРУ 3 Подставим 5 в F F F F O O F F F F f O O но это уравнение является тождеством так как FO FO F O F F F F f где первое уравнение в системе есть общее решение ОЛРУ а второе частное решение НЛРУ Пусть НЛРУ имеет вид РЕШЕНИЕ НЛРУ ПРИ ФУНКЦИИ-КОНСТАНТЕ 6 b где b — целое число константа Будем искать частное решение уравнения 6 в виде константы F c 7 то есть c — также целое число Подставим 7 в 6 c c c c b b c 8 Константа будет частным решением уравнения 6 при условии неравенства нулю знаменателя формулы 8 Введем характеристический полином для НЛРУ 6 Если h h то очевидно что уравнение 6 имеет частное решение
11 b F h Обозначим формальную производную характеристического полинома Тогда h h через h 9 h 3 Пусть h но h Будем искать решение 6 в виде F c 3 Подставляя 3 в 6 имеем c c c c b c b c h h b но h а h и b c h Итак если h то уравнение 6 имеет частное решение b F h Обозначим -ю производную h через h По определению будем считать h h Из курса алгебры известно что если число α является -кратным корнем многочлена h то h α Теперь частное решение 6 можно записать в виде b F 3 h где — кратность корня характеристического многочлена h Пример Решить уравнение 5 при F 35 Составляем ОЛРУ F Составляем характеристическое уравнение h 3 Решаем характеристическое уравнение 4 Записываем общее решение ОЛРУ F C C C C 5 Находим частное решение НЛРУ 5 F 5 h так как h 6 Записываем общее решение НЛРУ F F C C 5 7 С учетом начальных условий находим коэффициенты в решении НЛРУ
12 C C 5 C C 5 35 получаем C C 8 Записываем решение НЛРУ F 5 Итак мы получили явную формулу для вычисления -го члена последовательности В заключение вычислим саму последовательность: Будем искать частное решение НЛРУ РЕШЕНИЕ НЛРУ ПРИ ФУНКЦИИ-МНОГОЧЛЕНЕ F b 33 в виде многочлена той же степени что и в правой части F c 34 Подставляя 34 в 33 получим правило вычисления коэффициентов многочлена j c j b 35 j Приравнивая коэффициенты в левой и правой части при членах содержащих получаем Остальные коэффициенты c c b b c при h h находятся аналогично путем приравнивания коэффициентов при в 35 Если является корнем характеристического уравнения h кратности то частное решение НЛРУ следует искать в виде F c РЕШЕНИЕ НЛРУ ПРИ ФУНКЦИИ-ЭКСПОНЕНТЕ Будем искать частное решение НЛРУ F bα 37 в виде 36 Подставляя 38 в 37 имеем То есть F cα cα bα 38
13 bα F h α если α не является корнем характеристического уравнения h Если же α является корнем характеристического уравнения кратности то частное решение 37 следует искать в виде F dα где d — некоторая константа Пример При решении одной задачи теории кодирования установлена рекуррентная зависимость числа умножений M от числа итераций при построении проверочной матрицы кода M M 4 3 при M 7 Запишем ОЛРУ M M Тогда имеем характеристическое уравнение h и общее решение ОЛРУ M C Будем искать частное решение в виде M d e Подставляя его в исходное уравнение имеем e 4 3 Левая часть уравнения не содержит d и следовательно предлагаемое частное решение определено неверно так как корень характеристического уравнения Теперь изменим вид частного решения на M d e Подставляя его в исходное уравнение имеем e 3 d Таким образом M C 3 и учитывая начальные условия C 3 Итак решение исходного уравнения M 3 3 РЕКУРРЕНТНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА Рекуррентные уравнения отличные от линейных рекуррентных уравнений с постоянными коэффициентами не имеют общего метода решения Они могут решаться например методом проб и ошибок Рассмотрим нелинейное уравнение F F b при F b 39 Вычислим значение при подстановке в 39 некоторых констант F b b b при ; F F b b b при ;
14 b b b F F при 3 Теперь можно предположить что решением уравнения 39 является 4 og b F где Подставляя 4 в 39 имеем og og og b b b b b b F F og og j j b b Таким образом 4 действительно является решением уравнения 39
Видео:✓ Предел последовательности | матан #006 | Борис ТрушинСкачать

VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:2. Предел последовательностиСкачать

Разностное уравнение и рекуррентная последовательность
Будем обозначать через $ mathbb A_ $ какое-либо из множеств $ mathbb Z,mathbb Q, mathbb R_ $ или $ mathbb C_ $.
Видео:Предел последовательности #32Скачать

Линейное уравнение
Пример. Уравнение первого порядка $ x_=qx_ $ определяет — при задании $ x_ $ — геометрическую прогрессию.
Пример. Уравнение второго порядка
$$ x_=x_+x_K $$ определяет при $ x_0=1, x_1=1 $ последовательность чисел Фибоначчи — они обозначаются буквой $ F_ $ $$ _^infty= .$$
Пример. Разложение рациональной функции $ g_(x)/f(x) $ при $ f(x)=a_0x^n+dots+a_n $ и $ g_(x) $ — полиномах, $ deg g не зависит от коэффициентов $ g_(x) $). Подробнее ☞ ЗДЕСЬ.
Пример. Примером линейной рекуррентной последовательности $ n_ $-го порядка может служить последовательность сумм Ньютона полинома $ n_ $-й степени. Подробнее ☞ ЗДЕСЬ.
Задача. Решить разностное уравнение, т.е. найти выражение для $ x_ $ в виде явной функции от номера $ K_ $ и «начальных данных» $ x_0,dots,x_ $. Будем говорить об общем решении, если $ x_0,dots,x_ $ считаются произвольными.
Пример. Общее решение разностного уравнения $ x_=qx_ $ задается формулой $ x_K = q^K x_0 $.
Поставленную задачу можно обобщить, рассматривая более широкие классы разностных уравнений, как, например линейные неоднородные уравнения с переменными коэффициентами
$$ x_=a_1(K) x_+ dots+ a_n(K) x_K + b_(K) , n in mathbb N, K in , $$ где $ a_1(K),dots,a_n(K),b_n(K) $ — некоторые функции от номера $ K_ $. Примером таких рекуррентных последовательностей являются континуанты. Можно пойти еще дальше и рассматривать разностные уравнения, решениями которых являются не числа, а полиномы: $$kP_(x)-(2k-1),xP_(x)+(k-1),P_(x) equiv 0, quad kge 2 ; P_0(x)equiv 1, P_1(x) equiv x .$$ Полиномы $ < P_(x) > $, удовлетворяющие этому уравнению, известны как полиномы Лежандра.
Наконец, в некоторых разделах математики встречаются и нелинейные разностные уравнения, см. ☞ ЧИСЛА КАТАЛАНА.
Настоящий раздел посвящен, в основном, линейным уравнениям с постоянными коэффициентами.
Известны первые члены линейной рекуррентной последовательности:
$$ 0,1,2,2,0,-9,-38,-123,-360,-1004,-2728,-7303,ldots $$ Чему равен следующий?
Общий принцип решения подобных задач (т.е. как установить по последовательности вид линейного уравнения, которое ее, возможно, задает) ☞ ЗДЕСЬ.
Видео:11. Вычисление предела последовательности ( предел отношения двух многочленов ), примеры 1 и 2.Скачать

Идея решения
Решим сначала уравнение второго порядка $$ x_=p x_+q x_ npu qne 0 . $$ Сделаем из него — формальной заменой $ x_ rightarrow x^2, x_ rightarrow x, x_ rightarrow 1 $ — алгебраическое: $$x^2=pcdot x+qcdot 1 . $$ Анализируем корни:
1. Если дискриминант квадратного уравнения $ mathcal D=p^2+4q $ отличен от нуля, то его корни $ lambda_1,lambda_2 $ различны. Ищем решение разностного уравнения в виде $$ x_K=C_1lambda_1^K+C_2lambda_2^K , $$ где $ C_1,C_2 $ — некоторые, пока неопределенные, постоянные.
2. Если дискриминант $ mathcal D $ равен нулю (и при этом $ qne 0 $), то квадратное уравнение имеет единственный корень, который мы обозначим $ lambda_1 $. В этом случае решение разностного уравнения ищется в виде $$ x_K=(C_1 + C_2 K)lambda_1^K , $$ где $ C_1,C_2 $ — некоторые, пока неопределенные, постоянные.
В обоих случаях неопределенные коэффициенты $ C_1 $ и $ C_2 $ ищутся из «начальных условий»: получившиеся формулы должны оставаться справедливыми при $ K=0 $ и $ K=1 $. Таким образом, в случае 1 мы получим систему $$ left< begin x_0&=&C_1&+C_2, \ x_1&=&C_1lambda_1&+C_2lambda_2, end right. $$ решениями которой являются числа $$ C_1=frac, C_2= frac . $$ В случае 2 получаем систему $$ left< begin x_0&=&C_1, \ x_1&=&(C_1+C_2)lambda_1 end right. $$ с решениями: $$ C_1=x_0, C_2=frac-x_0 . $$
Теперь осталось показать, что найденные формулы действительно дают решение разностного уравнения. С этой целью формально подставим, например, первую из формул в уравнение: $$ x_=C_1lambda_1^+C_2lambda_2^ Rightarrow x_=C_1lambda_1^+C_2lambda_2^, x_=C_1lambda_1^+C_2lambda_2^ Rightarrow $$ $$ C_1lambda_1^+C_2lambda_2^ =p (C_1lambda_1^+C_2lambda_2^)+q(C_1lambda_1^+C_2lambda_2^) Rightarrow $$ $$ C_1lambda_1^(lambda_1^2-plambda_1-q)+ C_2lambda_2^(lambda_2^2-plambda_2-q)=0 . $$ Но, по предположению, $ lambda_j $ действительно является корнем квадратного уравнения $ x^2-px-q = 0 $. Следовательно, мы получили верное равенство, и решение может быть представлено в указанном виде. То, что это решение обеспечивает правильные «начальные данные» гарантировано тем способом, которым мы подбирали значения параметров $ C_1 $ и $ C_2 $.
Пример. Найти выражение для $ K_ $-го числа Фибоначчи.
Решение. Корни уравнения $$ x^2-x-1=0 $$ различны: $$ lambda_1 = frac<1+sqrt>, lambda_2=frac<1-sqrt> . $$ Следовательно, решение должно иметь вид $ x_K= C_1 lambda_1^K + C_2 lambda_2^K $. Константы $ C_1 $ и $ C_2 $ ищутся с помощью начальных данных: $$ x_0=C_1+C_2=1, x_1= C_1 lambda_1 + C_2 lambda_2 =1 . $$ Решив эту линейную систему, получим выражение $ K $-го числа Фибоначчи по формуле Бине: $$ F_K = frac<sqrt> left[ left( frac<1+sqrt> right)^ — left( frac<1-sqrt> right)^ right] . $$ ♦
Пример. Решить уравнение $$ x_=2, x_-2, x_ .$$ при $ x_1=2,x_2=2 $.
Решение. Соответствующее квадратное уравнение $ x^2-2 x + 2=0 $ имеет корни мнимые $ lambda_=1 pm mathbf i $. Согласно приведенному выше алгоритму, решение представляется в виде: $$ x_K=(1+mathbf i)^+(1-mathbf i)^ . $$ Здесь снова возникает парадоксальная ситуация: вещественная целочисленная последовательность представляется с помощью мнимых чисел. Разрешается «парадокс» теми же самыми рассуждениями, что и в предыдущем примере. Здесь можно пойти и дальше — избавиться от мнимой единицы. Поскольку $$ 1+ mathbf i = sqrt left( cos frac + mathbf i sin frac right), quad 1- mathbf i = sqrt left( cos left( — frac right) + mathbf i sin left(-frac right) right), $$ то применением формулы Муавра получаем: $$ x_K=2^ left( cos frac + mathbf i sin frac right) + $$ $$ qquad qquad + 2^left( cos left( — frac right) + mathbf i sin left(-frac right) right) = $$ $$ =2^ cos frac . $$ Таким образом, мы избавились от кажущейся мнимости ответа. То, что на самом деле полученное число является числом целым подтверждается тем, что последовательность $$ left_^ = left< 1, 2^,0,-2^,-1, -2^, 0, 2^, 1,dots right> $$ является циклической и выражения $ 2^ $ возникают только при четных $ K_ $. При домножении на $ 2^ $ дробные степени двойки пропадают. Резюмируем приведенные рассуждения: присутствие в ответе мнимой единицы, образно говоря, само является мнимым, иллюзорным; в вычислениях она участвует, но в ответе пропадает! ♦
Остался нераскрытым секрет получения общего алгоритма решения разностного уравнения. Очевидно, что алгоритм приводит к верному ответу (что подтверждается подстановкой найденного решения в уравнение), но откуда этот алгоритм взялся?!
Есть несколько подходов, приводящих к этому алгоритму — и самый общий, подходящий для уравнений произвольного порядка, изложен НИЖЕ. А в рассмотренном выше случае уравнения второго порядка, рассуждения могут быть следующими. Сделаем в уравнении $$ x_=p x_+q x_ $$ замену переменных так, чтобы получилось линейное уравнение первого порядка. С этой целью подберем параметры $ t_ $ и $ u_ $ так, чтобы последовательность $$ x_- t x_ =u ( x_- t x_) $$ совпала с исходной. Очевидно, что параметры $ t_ $ и $ u_ $ можно найти из системы уравнений $$ t+u=p, — tu=q . $$ Полученные формулы позволяют сделать вывод (см. ☞ формулы Виета), что $ t_ $ и $ u_ $ могут быть определены как корни квадратного уравнения $$ x^2-px-q=0 , $$ которое и возникло у нас «из ниоткуда» в приведенном выше алгоритме. Предположим, что корни этого уравнения различны. Обозначив их, как и ранее, $ t= lambda_1 $ и $ u= lambda_2 $, и введя в рассмотрение новую последовательность $ _^ $, связанную со старой формулой $$y_K= x_- lambda_1x_ , $$ мы получим уравнение для нее в виде $$ y_ =lambda_2 y_K . $$ Это уравнение снова разностное, но уже первого порядка, его решение нам известно (геометрическая прогрессия): $$ y_K = lambda_2^K y_0 . $$ Возвращаемся к исходной переменной — подставляем полученное в формулу, связывающую $ x_K $ и $ y_K $: $$ x_- lambda_1x_= lambda_2^K y_0 npu y_0=x_1- lambda_1 x_0 . $$ Мы снова получили разностное уравнение первого порядка, но, к сожалению, уже неоднородное. Попробуем его решить. Распишем разностное уравнение для последовательных значений $ K $: $$begin x_1-lambda_1x_0 &= & y_0 \ x_2-lambda_1x_1 &= & lambda_2y_0 \ x_3-lambda_1x_2 &= & lambda_2^2y_0 \ x_4-lambda_1x_3 &= & lambda_2^3y_0 \ dots & & dots end $$ Умножим первое уравнение на $ lambda_ $ и сложим со вторым, получим: $$ x_2-lambda_1^2 x_0 = (lambda_1+ lambda_2)y_0 . $$ Умножим это уравнение на $ lambda_1 $ и сложим с третьим: $$ x_3-lambda_1^3 x_0 = (lambda_1^2+lambda_1 lambda_2 + lambda_2)y_0 . $$ Продолжив процесс далее по аналогии, на $ K_ $-м шаге получим $$ x_-lambda_1^K x_0 = (lambda_1^+lambda_1^ lambda_2 +dots+ lambda_1^lambda_2^j+dots+ lambda_2^)y_0 . $$ В правой части полученного выражения стоит сумма геометрической прогрессии. Окончательно получаем: $$ x_K= x_0 lambda_1^K + frac(x_1- lambda_1 x_0) , $$ что полностью совпадает с приведенным выше результатом.
[Эйлер]. Доказать, что (в обозначениях настоящего пункта) имеет место утверждение: отношение
$$ frac<x_x_K-x_^2> $$ будет величиной постоянной, не зависящей от $ K_ $.
Видео:10 класс, 37 урок, Числовые последовательностиСкачать

Аналитика
Для разностного уравнения $$ x_=a_1 x_+ dots+ a_n x_K $$ алгебраическое уравнение, получающееся из него формальной заменой $$ begin x_ & x_ & dots & x_K \ downarrow & downarrow & dots & downarrow \ lambda^n & lambda^ & dots & 1 end $$ то есть уравнение $$ lambda^n — a_1 lambda^ — dots — a_n =0, $$ называется характеристическим уравнением (соответствующим данному разностному уравнению) 2) ; полином $$ f(lambda)= lambda^n — a_1 lambda^ — dots — a_n $$ будем называть характеристическим полиномом разностного уравнения. Обозначим $ lambda_,dots,lambda_n $ все корни этого полинома, с учетом их кратностей.
Теорема 1. Если все корни характеристического полинома различны, то решение разностного уравнения получается в виде
$$ x_= C_1lambda_1^K + dots+ C_n lambda_n^K , $$ числа $ C_,dots,C_n $ не зависят от $ K_ $ и определяются с помощью начальных условий из системы линейных уравнений: $$ left<begin C_1 &+C_2 &+dots &+ C_n &=& x_0 \ lambda_1 C_1 &+ lambda_2C_2&+dots & + lambda_n C_n & = & x_1 \ lambda_1^2 C_1 &+ lambda_2^2C_2&+dots & + lambda_n^2 C_n & = & x_2 \ dots &&&&& dots \ lambda_1^C_1 &+ lambda_2^C_2&+dots & + lambda_n^ C_n & = & x_. end right. $$
Теорема 2. Если характеристический полином имеет следующее разложение на линейные множители:
$$f(lambda)equiv (lambda-lambda_1)^<_1>times dots times (lambda-lambda_)^<_>, quad lambda_k ne lambda_ mbox k ne ell , _1 + dots + _ =n, $$ то общее решение разностного уравнения имеет вид: $$ x_=L_1(K)lambda_1^ +dots + L_(K)lambda_^ , $$ где $ L_1(K),dots,L_(K) $ — полиномы от $ K $ : $ L_p(K)in mathbb C[K], deg L_p 1. Если характеристический полином имеет единственный корень $ lambda_1 ne 0 $, т.е. $$ f(lambda)equiv (x-lambda_1)^n , $$ то общее решение разностного уравнения имеет вид: $$ x_=(C_1+C_2K+C_3K^2+dots+C_K^)lambda_1^K . $$ При заданных значениях $ x_0,x_1,dots,x_ $ величины $ C_1,dots,C_ $ могут быть определены из системы линейных уравнений, которая получается подстановкой в общее решение последовательных значений $ K in $: $$ left<begin x_0 &=& lambda_1^0&(C_1&+C_2cdot 0& + C_3cdot 0^2& + dots &+ C_ncdot 0^) \ x_1 &=& lambda_1^1&(C_1&+C_2cdot 1& + C_3cdot 1^2& + dots &+ C_ncdot 1^) \ x_2 &=& lambda_1^2&(C_1&+C_2cdot 2& + C_3cdot 2^2& + dots &+ C_ncdot 2^) \ dots & & dots \ x_&=& lambda_1^&(C_1&+C_2cdot (n-1)& + C_3cdot (n-1)^2& + dots &+ C_ncdot (n-1)^) end right. $$ Образно говоря: если получена общая закономерность, то она должна быть универсальной, т.е. сохраняться и в частных случаях.
Пример. Решить уравнение четвертого порядка $$x_=4,x_-6,x_+4,x_-x_ . $$
Решение. Характеристический полином $ (lambda-1)^4 $ имеет единственный корень $ lambda_1=1 $. Общее решение ищется в виде $ x_=C_1+C_2K+C_3K^2+C_4K^3 $, а при заданных начальных данных константы $ C_p $ определяются либо из приведенной выше системы линейных уравнений, либо же по одному из методов нахождения интерполяционного полинома. Так, для $ x_0=1,x_1=8,x_2=27,x_3=64 $ получаем $ C_1=1,C_2=3,C_3=3,C_4=1 $. Тогда выражение для общего члена рекуррентной последовательности $ x_=(K+1)^3 $ — ответ вполне ожидаемый, если обратить внимание на начальные данные… ♦
Статья не закончена!
Метод производящего ряда
В этом и следующем пунктах укажем два подхода, которые позволяют вывести естественным путем результаты, сформулированные в теоремах предыдущего пункта.
Распишем разностное уравнение $$ x_=a_1 x_+ dots+ a_n x_K $$ в бесконечную последовательность уравнений, положив $ K=0,1,2,dots $: $$ begin x_&-a_1 x_&-a_2 x_&- dots- a_n x_0&=&0, \ x_&-a_1 x_&- a_2 x_&- dots- a_n x_1&=&0, \ vdots & & & & & vdots \ x_&-a_1 x_&-a_2 x_&- dots- a_n x_K&=&0, \ dots & & &&&dots end $$ и дополним эту последовательность, поставив в ее начало еще $ n $ уравнений: $$ begin x_&&&&=&p_0, \ x_&-a_1 x_& &&=& p_1, \ x_&-a_1 x_&-a_2 x_& &=& p_1, \ vdots && & & & vdots \ x_&-a_1 x_&-a_2 x_&- dots- a_ x_0 &=& p_, end $$ При заданных начальных данных $ <x_0,x_1,dots,x_> $ из этих уравнений можно однозначно определить числа $ <p_0,p_1,dots,p_> $.
В объединенной системе произведем домножение уравнений на степени $ lambda $ $$ begin x_&&&&&=&p_0, & times 1 \ x_&-a_1 x_&& &&=& p_1, & times lambda \ x_&-a_1 x_&-a_2 x_& &&=& p_1, & times lambda^2 \ vdots && & & && vdots & vdots \ x_&-a_1 x_&-a_2 x_&- dots- a_ x_0 &&=& p_, & times lambda^ \ x_&-a_1 x_&-a_2 x_&- dots — a_ x_1 & — a_n x_0&=&0, & times lambda^ \ x_&-a_1 x_&- a_2 x_&- dots — a_ x_2 & — a_n x_1&=&0, & times lambda^ \ vdots & & & dots & & & dots & vdots \ x_&-a_1 x_&-a_2 x_&- dots- a_ x_ &- a_n x_K&=&0, & times lambda^ \ dots & & && &&dots & dots end $$ и сложим эти уравнения, собирая по столбцам коэффициенты при $ a_1,dots, a_n $.
Ряд $$ Z(lambda)=sum_^x_lambda^j=x_0+x_1lambda+x_2lambda^2+dots+x_K lambda^K + dots $$ называется производящим рядом рекуррентной последовательности.
Мы получили для него уравнение $$ Z(lambda)-a_1lambda Z(lambda)-a_2lambda^2Z(lambda)-dots — a_nlambda^n Z(lambda)equiv p_0+p_1lambda+p_2lambda^2+dots+p_lambda^ , $$ или $$ Z(lambda)(1-a_1lambda-a_2lambda^2-dots- a_nlambda^n) equiv P(lambda) , $$ где $ P(lambda)=p_0+p_1lambda+p_2lambda^2+dots+p_lambda^ $ — известный полином. Таким образом производящий ряд получается разложением в ряд по степеням $ lambda $ рациональной функции $$ frac
$$ и, если нам удастся найти явное выражение для коэффициента при $ lambda^K $, то он и будет решением разностного уравнения.
Полином $ f^(lambda) = 1-a_1lambda-a_2lambda^2-dots- a_nlambda^n $ не совпадает с характеристическим полиномом $ f(lambda)= lambda^n-a_1lambda^-a_2lambda^- dots — a_n $ разностного уравнения, но очень на него похож: они связаны соотношением $$ f^(lambda) equiv lambda^n f(1/lambda) , $$ и корни $ f^(lambda) $ равны обратным величинам корней полинома $ f(lambda) $, т.е. $ 1/lambda_1,dots,1/lambda_n $ (см. свойство 3 ☞ ЗДЕСЬ ). Если все эти корни различны, то дробь $ 1/f^(lambda) $ может быть разложена на простейшие дроби вида: $$ frac<f^(lambda)>=frac = $$ $$ =frac+frac+dots+frac , $$ где $ gamma_1, gamma_2,dots, gamma_n $ — комплексные числа, которые можно однозначно выразить через $ lambda_1,dots,lambda_n $ (эти выражения для дальнейшего несущественны). Теперь каждую простейшую дробь раскладываем в степенной ряд: $$ frac=gamma_j left(1+lambda_j cdot lambda+ lambda_j^2 cdot lambda^2+dots+ lambda_j^K cdot lambda^K+dots right) $$ и, следовательно, получаем разложение для производящего ряда $$ Z(lambda)=frac
= $$ $$ =P(lambda) left[ (gamma_1+dots+gamma_n)+(gamma_1lambda_1+dots+gamma_nlambda_n)lambda+dots+(gamma_1lambda_1^K+dots+gamma_nlambda_n^K)lambda^K + dots right] . $$ Вытаскиваем из него коэффициент при $ lambda^K $: $$ begin p_0 (gamma_1lambda_1^K &+dots+&gamma_nlambda_n^K)+ \ +p_1(gamma_1lambda_1^&+dots+&gamma_nlambda_n^)+ \ &+dots + &\ +p_ (gamma_1lambda_1^&+dots+&gamma_nlambda_n^)= end $$ и просуммируем по столбцам: $$ begin = gamma_1lambda_1^K (p_0+p_1/lambda_1+dots+p_/lambda_1^)+\ + gamma_2lambda_2^K (p_0+p_1/lambda_2+dots+p_/lambda_2^)+ \ +dots + \ + gamma_nlambda_n^K (p_0+p_1/lambda_n+dots+p_/lambda_n^)= end $$ $$ =gamma_1 P(1/lambda_1)lambda_1^K+ gamma_2 P(1/lambda_2)lambda_2^K +dots + gamma_n P(1/lambda_n)lambda_n^K . $$ Обозначив $ C_j = gamma_j P(1/lambda_j) $ при $ jin $, мы получим общее решение разностного уравнения приведенное в теореме 1 предыдущего пункта.
Метод производящего ряда позволяет решать и неоднородные разностные уравнения.
Пример. Решить уравнение $$x_=3,x_-2,x_+(K+1)(K+2) . $$
Ответ. $ x_K=2^K(x_1-x_0+8)-1/3(K+3)(K^2+3,K+8)+2,x_0-x_1 $.
Статья не закончена!
Метод матричной степени
Пусть рекуррентная последовательность задается уравнением $$ x_=a_1 x_+ dots+ a_n x_K $$ и начальными данными $ x_0,x_1,dots,x_ $.
Введем в рассмотрение столбцы, состоящие из $ n_ $ последовательных элементов этой последовательности, обозначив $$ X_0=left( begin x_0 \ x_1 \ vdots \ x_ end right), X_1=left( begin x_1 \ x_2 \ vdots \ x_ end right), X_2=left( begin x_2 \ x_3 \ vdots \ x_ end right), dots, X_K=left( begin x_K \ x_ \ vdots \ x_ end right),dots ; $$ а также следующую матрицу, известную как матрица Фробениуса: $$ = left( begin 0 & 1 & 0 & 0 & dots & 0 & 0 \ 0 & 0 & 1 & 0 & dots & 0 & 0 \ 0 & 0 & 0 & 1 & dots & 0 & 0 \ dots& &&&ddots & & dots \ 0 & 0 & 0 & 0 & dots & 0 & 1 \ a_n & a_ & a_ & & dots & a_2 & a_1 end right)_ $$ Используя правило умножения матриц, а также соотношение между элементами последовательности, получаем: $$ X_1=X_0, X_2=X_1,dots, X_K=X_,dots, $$ откуда имеем: $$ X_K=^KX_0 quad npu quad Kin mathbb N . $$ Искомое выражение для $ x_ $ получится умножением первой строки матрицы $ ^K $ на столбец начальных данных $ X_ $. Таким образом, задача решения разностного уравнения сводится к задаче возведения в степень матрицы $ $.
Для нахождения $ ^ $ воспользуемся результатами пункта СТРУКТУРА СТЕПЕННОЙ ФУНКЦИИ. Найдя жорданову нормальную форму (ЖНФ) $ _ $ и соответствующую матрицу преобразования базиса $ C_ $, получим $$ _ =C^ mathfrak F C Longrightarrow ^=C _<_>^ C^ , . $$ Характеристический полином матрицы Фробениуса: $$det (- lambda E)= (-1)^n(lambda^n-a_1 lambda^-dots-a_n) . $$ с точностью до знака совпадает с характеристическим полиномом последовательности. Обозначим его корни $ lambda_1,dots,lambda_n $. Если они различны, то жорданова нормальная форма $ _<_> $ диагональна. Если же среди этих корней имеются кратные, то установление структуры ЖНФ потребует усилий; однако же можно заранее утверждать, что эта форма диагональной не будет.
Подробный дальнейший анализ (с выводом теорем $ 1_ $ и $ 2_ $ из пункта АНАЛИТИКА) ☞ ЗДЕСЬ.
Cистемы линейных разностных уравнений
Подход предыдущего пункта можно успешно распространить на системы линейных разностных уравнений.
Пример. Решить систему разностных уравнений
Решение. Имеем: $$ left( begin x_ \ y_ end right) = left( begin 1 & 2 \ 3 & 2 end right) left( begin x_ \ y_ end right)= left( begin 1 & 2 \ 3 & 2 end right)^2 left( begin x_ \ y_ end right)=dots= left( begin 1 & 2 \ 3 & 2 end right)^K left( begin x_ \ y_ end right) . $$ Возводим матрицу в степень по методу, изложенному в разделе ☞ ВЫЧИСЛЕНИЕ ФУНКЦИИ ОТ МАТРИЦЫ. Ее характеристический полином $ f(lambda)=lambda^2-3, lambda — 4 $ имеет корни $ $. Соответствующие собственные векторы $ [1,-1]^ $ и $ [2,3]^ $. Следовательно: $$ left( begin 1 & 2 \ 3 & 2 end right)^K= left( begin 1 & 2 \ -1 & 3 end right) left( begin (-1)^K & 0 \ 0 & 4^K end right) left( begin 1 & 2 \ -1 & 3 end right)^ = $$ $$ =frac left( begin 3cdot (-1)^K + 2 cdot 4^K & 2 cdot (-1)^ + 2 cdot 4^K \ 3cdot (-1)^ + 3 cdot 4^K & 2 cdot (-1)^ + 3 cdot 4^K end right) . $$ Домножение этой матрицы на столбец $ [x_0,y_0]^=[1,-1]^ $ приводит к ответу $ x_K=(-1)^K, y_K=(-1)^ $, который немедленно проверяется «вручную» .
Приведем альтернативное решение настоящего примера — «разделим» переменные. Сделаем подстановку $ K to K+1 $ в первом уравнении: $$ x_=x_K+2,y_K=(x_ +2,y_)+2, (3,x_+2,y_)=7,x_+6,y_ . $$ Теперь из двух уравнений — нового и исходного — исключим $ y_ $: $$ left< begin x_&-x_ &= & 2,y_ \ x_&-7,x_&=&6,y_ end right. quad Rightarrow quad x_-3,x_-4,x_=0 . $$ Мы получили разностное уравнение второго порядка относительно величины $ x_ $. Совершенно такое же уравнение получается и относительно другой переменной: $ y_-3,y_-4,y_=0 $. Характеристический полином этого уравнения совпадает с характеристическим полиномом матрицы. Различие между генерируемыми этим уравнением рекуррентными последовательностями $ _^ $ и $ _^ $ будет определяться только начальными данными. ♦
Пример. Решить систему разностных уравнений
Видео:Предел последовательности #19Скачать

Асимптотика
Задача. Как ведет себя рекуррентная последовательность $ _^ $ при возрастании $ K $?
Если при любых $ x_0,dots,x_ $ решение $ x_K $ уравнения $$ x_=a_1 x_+ dots+ a_n x_K $$ ограничено, то будем называть это уравнение устойчивым. Устойчивое уравнение называется асимптотически устойчивым если $$ x_K to 0 quad npu quad K to infty .$$ Уравнение называется неустойчивым, если существует хотя бы один набор $ x_0,dots,x_ $, для которого соответствующая последовательность $ x_K $ неограничена.
Для анализа асимптотики $ $ при $ K to infty $ обратимся к приведенным ☝ ВЫШЕ теоремам 1 и 2, в которых общее решение разностного уравнения выражено через корни $ lambda_1,dots,lambda_n $ его характеристического уравнения.
Теорема. Уравнение $$ x_=a_1 x_+ dots+ a_n x_K $$ будет
а) устойчивым тогда и только тогда, когда $ |lambda_j| le 1 $ для любого $ j_ $, и собственные числа, имеющие модуль равный $ 1_ $, являются простыми для характеристического полинома;
б) асимптотически устойчивым тогда и только тогда, когда $ |lambda_j| ☞ ЗДЕСЬ. Условие $ 0 1. Пусть $ qne p $. Применяем теорему 1: $$u(K,N)=C_1 1^K+C_2 (q/p)^K=C_1+C_2 (q/p)^K .$$ Константы $ C_j $ находим из граничных условий: $$ left< begin C_1+C_2&=&0 \ C_1+(q/p)^NC_2&=&1 end right. Longrightarrow C_1=-C_2=frac $$ $$Longrightarrow u(K,N)= frac quad npu Kin .$$
2. Пусть теперь $ q=p=frac $ (проигрыш и выигрыш равновероятны). Применяем теорему 2: $ u(K,N)=(C_1+C_2K)cdot 1^ $; константы находим из граничных условий: $ C_1=0,C_2=1/N $. Следовательно: $$u(K,N)=K/N quad npu Kin .$$
Теперь проанализируем полученные решения. Во втором случае выигрыш тем вероятнее, чем больше стартового капитала имеет игрок, и при $ K>N/2 $ игрок скорее выиграет. В первом случае анализ ситуации несколько сложнее, хотя зависимость вероятности выигрыша от размера стартового капитала сохраняется. Рассмотрим более интересный случай $ p 3) $ 10 $, но тогда можно и не играть! При $ N=100,p=frac,q=frac $ и при капитале $ K=99 $ игроку имеет смысл вести игру: его выигрыш до $ 100 $ более вероятен, чем разорение «до нитки». А вот при $ K=98 $ лучше не рисковать!
При каком соотношении $ p_ $ и $ q_ $ ($ p ☞ АНАЛИТИКА общее решение разностного уравнения позволяет построить и общее решение дифференциального уравнения. В самом деле, если $ lambda_^ $ — какой-то из корней характеристического уравнения $ lambda^n — a_1lambda^-dots-a_lambda — a_n=0 $, то одним из решений разностного уравнения будет $ u_K=Clambda_^K $ при $ Kin mathbb N $ и произвольной константе $ Cin mathbb C $. Тогда ряд $$ y(x)=sum_^ u_j frac = C sum_^ frac<lambda_^jx^j>=Ce^ <lambda_x> $$ дает один из интегралов дифференциального уравнения. Если все корни $ lambda_,dots,lambda_n $ характеристического уравнения простые, то общий интеграл дифференциального уравнения будет иметь вид $$ C_1 e^ + dots + C_n e^ . $$ Если же среди корней характеристического уравнения имеются кратные, то общий интеграл записывается в виде $$ tilde L_1(x)e^ + dots + tilde L_(x) e^ <lambda_x> , $$ где $ tilde L_1(x),dots,tilde L_(x) $ — полиномы по $ x_ $, $ _^ subset mathbb C[x], deg tilde L_j ♦
Метод конечных разностей
Пример. Найти решение дифференциального уравнения $$ y^ -3, y^ + 4, y=0 , $$ удовлетворяющее условиям $ y(0)=0, y(1)=1 $, и вычислить значение $ y(0.5) $.
В отличие от задачи Коши предыдущего пункта, где нас интересовало решение с известными начальными данными, мы теперь имеем дело с, так называемой, краевой задачей для обыкновенного дифференциального уравнения.
Решение. Для данного примера удается построить точное решение: $$ y(x)=frac< e^sin (sqrt/2 x )><sin (sqrt/2)> quad u quad y( 1/2) approx 0.299303 . $$ Наша задача сейчас — проиллюстрировать приближенный метод решения краевой задачи (а полученное аналитическое решение будем использовать для контроля точности). Этот метод заключается в дискретизации непрерывного процесса — вместо нахождения общего выражения для решения $ y(x) $, подобного только что представленному, мы ставим целью нахождение значений $ y(x_j) $ в некоторых точках интервала $ [0_,1] $. Разобьем этот интервал на $ N_ $ равных частей точками $$ x_j=j h quad npu quad jin , h=1/N . $$ Вспомнив определение производной функции как предела: $$ y^(x)= lim_ frac $$ будем считать, что при достаточно малых значениях $ h_>0 $, ошибка в равенствах $$ y^(x_j) approx frac quad u quad y^(x_j) approx frac $$ пренебрежимо мала. Таким образом, мы получаем приближение для производной (неизвестной нам функции) через значения этой же функции. Какое из двух этих приближений взять — не очень принципиально. С целью «сохранения равноправия» в окрестности $ x_ $, возьмем в качестве приближения $$ y^(x_j) approx frac left( frac + frac right) = frac . $$ Для значения второй производной $ y^(x) $ в точке $ x_ $ приближение строим в виде $$ y^(x_j) approx frac left( frac — frac right)= $$ $$ = frac<y(x_+h)-2y(x_j)+y(x_j-h)> . $$ С использованием этих приближений, а также обозначения $$ u_j = y(x_j) quad npu quad j in , $$ заменяем исходное дифференциальное уравнение на уравнение $$ (u_-2, u_j — u_) — frac h (u_- u_)+4 h^2 u_j iff $$ $$ iff quad (1-3/2h) u_+ (4,h^2-2)u_j+ (1+3/2h) u_= 0 , $$ которое является линейным разностным уравнением второго порядка. Граничные условия для дифференциального уравнения переходят в граничные условия для разностного: $ u_0=0,u_N=1 $. Можно решить это уравнение в явном виде — по аналогии с тем, как это было сделано в пункте ☞ ЗАДАЧА О РАЗОРЕНИИ ИГРОКА. Но мы пойдем другим путем и для нахождения значений $ u_1,dots,u_ $ выпишем получившиеся линейные уравнения. Так, для $ N=6 $ уравнения $$ 3/4 u_-17/9 u_ + 5/4 u_ = 0 quad npu quad jin $$ перепишутся в виде $$ left< begin 3/4 u_6 & — 17/9 u_5 &+5/4 u_4 & & & & = 0, \ & 3/4 u_5 & — 17/9 u_4 &+5/4 u_3 & & & =0, \ & & 3/4 u_4 & — 17/9 u_3 &+5/4 u_2 & & =0, \ & & & 3/4 u_3 & — 17/9 u_2 &+5/4 u_1 & =0, \ & & & & 3/4 u_2 & — 17/9 u_2 &+5/4 u_0 =0. end right. $$ С учетом граничных условий, перепишем эту систему в матричном виде $$ left( begin — 17/9 & 5/4 & & & \ 3/4 & — 17/9 & 5/4 & & \ & 3/4 & — 17/9 & 5/4 & \ & & 3/4 & — 17/9 &5/4 \ & & & 3/4 & — 17/9 end right) cdot left( begin u_5 \ u_4 \ u_3 \ u_2 \ u_1 end right)= left( begin -3/4 \ 0 \ 0 \ 0 \ 0 end right) $$ (все неуказанные элементы матрицы равны $ 0_ $). Матрица системы является трехдиагональной. Существуют специальные методы решения систем линейных уравнений с подобными матрицами (см. ☞ метод прогонки ). Но мы ограничимся здесь только поставленной задачей оценки величины $ y(0.5) $. Очевидно, для этого необходимо «вытащить» из системы значение неизвестной $ u_3 $. Сделаем это с помощью формул Крамера: $$ u_3= frac< left| begin — 17/9 & 5/4 & -3/4 & & \ 3/4 & — 17/9 & 0 & & \ & 3/4 & 0 & 5/4 & \ & & 0 & — 17/9 &5/4 \ & & 0 & 3/4 & — 17/9 end right| ><left| begin — 17/9 & 5/4 & & & \ 3/4 & — 17/9 & 5/4 & & \ & 3/4 & — 17/9 & 5/4 & \ & & 3/4 & — 17/9 &5/4 \ & & & 3/4 & — 17/9 end right|> = frac approx 0.295665 , $$ что неплохо согласуется с точным ответом.
При выборе $ N = 8 $ (более мелком дроблении интервала) получаем новое разностное уравнение $$ 13 u_-31 u_ + 19 u_ = 0 quad npu quad jin , $$ которое относительно $ u_ $ будет иметь решение $$ u_4=frac approx 0.297290 . $$ ♦
алгебраическое уравнение $ leftrightarrow $ линейное разностное уравнение $ leftrightarrow $ линейное дифференциальное уравнение.
Так, в двух последних пунктах решения двух задач из теории линейных дифференциальных уравнений — задачи Коши и краевой задачи — свелись к решению линейных разностных уравнений. В следующем пункте мы упрочим связи между алгебраическим и разностным уравнениями.
Видео:10 класс, 38 урок, Предел числовой последовательностиСкачать

Поиск корня полинома методом Бернулли
В разных разделах алгебры (и не только алгебры) слово «решить» может иметь совершенно разный смысл. Поставленная в начале настоящего раздела задача о решении линейного разностного уравнения свелась к нахождению корней его характеристического полинома. Вид общего решения найден и в этом смысле решение задачи получено. Вспомним, однако, что в общем случае нахождение корней полинома представляет собой отдельную задачу, которую также должно решать! Но известно, что корни полинома степени выше четвертой, как правило, не могут быть выражены в виде «хороших» функций от коэффициентов этого полинома (см. ☞ РЕШЕНИЕ УРАВНЕНИЙ В РАДИКАЛАХ ) ; мы можем гарантировать разве что их приближения с заданной точностью… Иными словами, мы свели решение одной задачи (решения разностного уравнения) к другой задаче (решения алгебраического уравнения), которая не имеет «красивого» решения!
Кажется, что мы влипли в порочный круг 4) . На самом деле, ситуация не столь безнадежна. Во-первых, хотя бы в некоторых случаях решение может быть получено явно — когда корни характеристического полинома удается найти в радикалах. Во-вторых, кое-какую пользу от полученного теоретического решения задачи мы получили и для общего случая. Например, мы смогли проанализировать поведение последовательности при возрастании $ K $ — и смогли сделать это «честно»: не привлекая бесконечные процессы численных методов, а только производя конечный набор элементарных операций над коэффициентами характеристического полинома.
В настоящем пункте мы «развернем» приведенную в пункте ☞ АНАЛИТИКА схему решения, сводящую разностное уравнение к алгебраическому: именно, мы будем искать корень алгебраического уравнения с помощью рекуррентной последовательности.
Задача. Решить алгебраическое уравнение $$ x^n+a_1x^+a_2x^ + dots + a_n = 0 . $$ Здесь коэффициенты $ a_1,dots,a_n ne 0 $ предполагаются комплексными.
Теорема [Бернулли]. Обозначим $ lambda_1 $ — максимальный по модулю корень уравнения
$$ x^n+a_1x^+a_2x^ + dots + a_n = 0 . $$ Предположим, что остальные корни уравнения строго меньше этого корня по модулю: $$ |lambda_1 | > |lambda_j | quad npu jin . $$ Тогда линейная рекуррентная последовательность $$ x_=-a_1x_-a_2x_-dots-a_nx_ $$ практически для любых начальных данных $ x_0,dots,x_ $ будет обладать свойством $$ lim_ frac<x_><x_> = lambda_1 , $$ т.е. отношение двух соседних членов последовательности будет стремиться к максимальному по модулю корню алгебраического уравнения.
Доказательство. Предположим сначала, что корни алгебраического уравнения все различны. Тогда это уравнение является характеристическим для рекуррентной последовательности $$ x_=-a_1x_-a_2x_-dots-a_nx_ $$ и, на основании теоремы 1 общий член этой последовательности может быть представлен в виде: $$ x_K=C_1lambda_1^K+C_2lambda_2^K+dots+C_nlambda_n^K . $$ Тогда $$ frac<x_><x_> =frac<C_1lambda_1^+C_2lambda_2^+dots+C_nlambda_n^ > =frac<displaystyle<lambda_1^Kleft(C_1+C_2left(fracright)^K+dots+C_nleft(fracright)^K right) >><displaystyle<lambda_1^left(C_1+C_2left(fracright)^+dots+C_nleft(fracright)^right)>> . $$ По условию теоремы $ |lambda_j/ lambda_1| ♦
Итак, для решения алгебраического уравнения предлагается «запустить» рекуррентную последовательность. А почему бы и нет? Такая последовательность достаточно просто реализуется — пусть себе компьютер считает!
Пример. Вычислить максимальный по модулю корень полинома
Решение. Образуем разностное уравнение пятого порядка: $$ x_=-20,x_-50, x_-(6+7)x_-129x_K $$ и возьмем в качестве начальных данных набор значений $$ x_0=0,x_1=0,x_2=0,x_3=1,x_4=43/149+5/2 . $$ Получаем: $$ begin K & x_ & approx x_/x_ \ hline 0 & -860/149 & -0.263005+2.278364, \ 1 & -1425/149+2150/149 , & 1.656976-2.5, \ 2 & 29394/149-84957/149 , & -33.750155+8.697660 , \ 3 & -1357017/298+1630426/149 , & -19.607285-1.202631, \ 4 & 17818407/149-62193575/298 , & -20.133934-2.549861 , \ 5 & -438023980/149+588013250/149 , & -20.311478-2.447384, \ 6 & 10315906213/149-10869371284/149 , & -20.292875-2.427054 , \ 7 &-235730478967/149+390960600447/298 , & -20.290782-2.430009 , \ 8 & 5258315203898/149-3393662220742/149 , & -20.291221-2.430198 , \ 9 & -114944764751262/149+112166341785085/298 , & -20.291233-2.430136 , end $$ На рисунке голубым цветом изображены пять первых элементов последовательности $ x_/x_ $, корни полинома обозначены красным. 
При каком наборе начальных данных последовательность $ x_/x_ $ будет сходиться
а) к третьему по величине модуля корню полинома;
б) к минимальному по модуля корню полинома?
Как решить последнюю задачу в общем случае: модифицировать алгоритм так, чтобы находить минимальный по модулю корень полинома?
Подсказка. См. ☞ ЗДЕСЬ.
Теперь посмотрим что произойдет, если нарушается условие единственности корня с максимальным модулем. Такая ситуация может показаться исключительной для полиномов с коэффициентами мнимыми. Так оно и есть: корни такого полинома располагаются на комплексной плоскости случайным образом и вероятность того, что два из них окажутся на одной и той же окружности с центром в точке 0 пренебрежимо мала. Однако, если мы имеем дело с полиномами с коэффициентами вещественными (а этот случай чаще предыдущего встречается в практике вычислений), то ситуация равенства модулей двух корней полинома становится уже не исключительной: комплексно-сопряженные пары корней имеют одинаковые модули (см. ☞ ЗДЕСЬ )!
Пример. Вычислить максимальный по модулю корень полинома
Решение. Запускаем рекуррентную последовательность $$ x_=7,x_-34,x_+68, x_-40,x_ $$ с различными начальными данными $$ begin x_0=0,x_1=0,x_2=0,x_3=6 \ hline begin K & approx x_/x_ \ hline 0 & 7 \ 1 & 2.142857 \ 2 & -4.333333 \ 3 & 8.138461 \ 4 & 1.423440 \ 5 & -10.219123 \ 6 & 5.990253 \ 7 & 0.672328 \ 8 & -25.714336 end end begin x_0=0,x_1=0,x_2=1,x_3= \ hline begin approx x_/x_ \ hline 7+34 \ 4.883817+0.564315 \ 0.398454+0.417510 \ -18.958354+23.801257 \ 4.302668+0.516309 \ -0.631595+0.556795 \ 21.917361+15.773371 \ 3.407653+0.432279 \ -1.771117+0.731887 end end $$ Сходимость неочевидна. Анализируем корни полинома: $$ lambda_1=2-4 , lambda_2=2+4 ,lambda_3=2, lambda_4=1 .$$ Имеется два максимальных по модулю корня и они комплексно-сопряженные. Теперь понятно почему не должна сходиться первая последовательность: ее начальные данные были все вещественными, вещественными же являются коэффициенты полинома (и разностного уравнения), следовательно последовательность $ x_/x_ $ не могла генерировать мнимые числа в принципе! Вторая последовательность состоит из мнимых чисел, и доказать отсутствие сходимости хотя бы к одному из корней $ lambda_1 $ или $ lambda_2 $ уже посложнее. ♦
Видео:Предел последовательности #27Скачать

Алгоритм «деления-вычитания» вычисления корней полинома
Иногда мелкий результат служит отправной точкой для крупной теории… Числа Фибоначчи просто задаются — а какую теорию порождают! Имея в виду это обстоятельство, вернемся к упражнению Эйлера в конце ☞ ПУНКТА.
Сгенерируем на основе рекуррентной последовательности $$ x_=-a_1x_-a_2x_-dots-a_nx_ $$ новую последовательность $$ y_=x_x_-x_^2 . $$ На примерах из предыдущего пункта оценим асимптотику отношения $$ frac<y_> quad npu quad K to infty . $$
Пример. Для полинома
$$ f(x)= x^5+20,x^4-50,x^3-(6+7),x-129 $$ разностное уравнение $$ x_=-20,x_-50, x_-(6+7)x_-129x_K $$ при выборе начальных данных $$ x_0=0,x_1=0,x_2=0,x_3=1,x_4=43/149+5/2 $$ дает: $$ begin K & approx y_ & approx y_/y_ \ hline 5 & -1021.889329+3566.979865 , & \ 6 & 171845.562159+54605.729066 , & 1.392427-48.575679 , \ 7 & 3593515.455351-9699634.071978 , & 2.702763-57.302733 ,\ 8 & & 2.056010-56.461741 , \ 9 & & 1.577875-55.791210 , \ vdots & & dots \ 12 & & 1.673367-55.241399 , \ vdots & & dots \ 15 & & 1.631486-55.261773 , \ vdots & & dots \ 18 & & 1.642333-55.263835 , \ vdots & & dots \ 24 & & 1.640619-55.263355 , end $$ Видим, что имеется сходимость к какому-то мнимому числу. Оказывается, это число равно произведению двух максимальных по модулю корней полинома $ f(x) $: $$ lambda_1 lambda_2 approx (-20.291225-2.430137 ,) (0.241854+2.694544,) approx $$ $$ approx 1.640589-55.263344 , . $$ Проверим теперь полином $ x^4-7,x^3+34,x^2-68,x+40 $, у которого два комплексно-сопряженных корня имеют одинаковое значение модуля. $$ begin x_0=0,x_1=0,x_2=0,x_3=6 & x_0=0,x_1=0,x_2=1,x_3= \ hline begin K & approx y_/y_ \ hline 5 & 17.882352 \ 6 & 18.988157 \ 7 & 20.085510 \ 8 & 20.252126 \ dots & dots \ 12 & 19.993988 \ dots & dots \ 16 & 19.999734 end & begin approx y_/y_ \ hline 19.191066+0.225090 , \ 19.040624+0.076125 , \ 19.769628-0.020615 , \ 20.115168-0.025721 , \ dots \ 19.991971+0.000361 , \ dots \ 19.999996+0.000032, end end $$ Гипотеза подтверждается: последовательность сходится к квадрату модуля корней. ♦
Теорема. Обозначим $ lambda_1, lambda_2 $ — максимальные по модулю корни уравнения
$$ x^n+a_1x^+a_2x^ + dots + a_n = 0 . $$ Предположим, что остальные корни уравнения строго меньше этого корня по модулю: $$ |lambda_1 | ge |lambda_2 |> |lambda_j | quad npu jin . $$ Тогда линейная рекуррентная последовательность $$ x_=-a_1x_-a_2x_-dots-a_nx_ $$ — практически для любых начальных данных $ x_0,dots,x_ $ будет обладать свойством $$ lim_ frac<x_x_-x_^2><x_x_-x_^2> = lambda_1 lambda_2 . $$
Доказательство. Предположим для простоты, что все корни $ lambda_3,dots,lambda_n $ различны. Тогда, используя рассуждения аналогичные приведенным в доказательстве теоремы Бернулли , получаем $$ x_x_-x_^2=C_1C_2left(frac-1 right)^2lambda_1^lambda_2^K + dots , $$ где многоточие в правой части означает слагаемые, возрастающие при $ K to infty $ более медленно, чем выделенное . Перейдя от $ K $ к $ K+1 $, и составив отношение из условия теоремы, мы получим доказываемый результат. Исключительных случаев оказывается два: либо одна из констант $ C_j $ обратится в нуль за счет неудачного выбора начальных данных $ x_0,dots,x_ $; либо же $ lambda_2=lambda_1 $, т.е. уравнение обладает кратным корнем. Последняя ситуация требует более тонкого анализа, но всегда может быть обезврежена предварительной проверкой уравнения на наличие кратных корней (если у уравнения имеется кратный корень, то, как правило, его можно выразить рационально через коэффициенты ). ♦
Объединим теперь результаты последней теоремы и теоремы Бернулли:
Второй по убыванию модуля корень уравнения может быть получен с помощью линейной рекуррентной последовательности
Как обобщить этот результат для нахождения следующих корней уравнения? — Для этого требуется аппарат ганкелевых определителей.
Теорема. Составим из элементов рекуррентной последовательности
$$ x_=-a_1x_-a_2x_-dots-a_nx_ $$ определитель третьего порядка: $$ H_K=left|begin x_ & x_ & x_ \ x_ & x_ & x_ \ x_ & x_ & x_ end right| . $$ Тогда, если через $ lambda_1,lambda_2,lambda_3 $ обозначить максимальные по модулю корни уравнения $$ x^n+a_1x^+a_2x^ + dots + a_n = 0 , $$ то, как правило, $$ lim_ frac<H_> = lambda_1lambda_2lambda_3 . $$
Третий по убыванию модуля корень уравнения может быть получен с помощью линейной рекуррентной последовательности
Видео:Математический анализ: Числовая последовательностьСкачать

Задачи
Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Источники
[1]. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.Наука. 1966
[2]. Гельфонд А.О. Исчисление конечных разностей. М.Наука. 1967
[3]. Шеннон К. Математическая теория связи. (Shannon C.E. A Mathematical Theory of Communication. Bell System Technical Journal. — 1948. — Т. 27. — С. 379-423, 623–656.)
[4]. Марковъ А. Исчисленie конечныхъ разностей. Mathesis. 1910
[5]. Гурса Э. Курс математического анализа. Т.2. М.-Л.ГТТИ. 1933
🎥 Видео
Предел числовой последовательности. Практическая часть. 10 класс.Скачать

Предел последовательности #1Скачать