Данный калькулятор предназначен для определения взаимного расположения двух плоскостей в пространстве онлайн.
Две плоскости могут иметь три варианта взаимного расположения относительно друг друга. Во-первых, плоскости могут быть параллельны. Во-вторых, они могут быть перпендикулярны. В таком случае угол между плоскостями равен 90 градусам. В-третьих, плоскости могут пересекаться, образовывая при этом два острых и два тупых угла.
Таким образом, с помощью данного калькулятора определяется следующее: пересекаются или нет плоскости, и, если они пересекаются, то перпендикулярны ли они.
Чтобы ответить на вопрос о взаимном расположении плоскостей, необходимо ввести уравнения заданных плоскостей в калькулятор и нажать кнопку «Вычислить».
- Точка пересечения прямых в пространстве онлайн
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
- 🌟 Видео
Видео:15. Взаимное расположение прямых в пространствеСкачать

Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
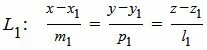 , , | (1) |
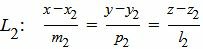 , , | (2) |
Найти точку пересечения прямых L1 и L2 (Рис.1).
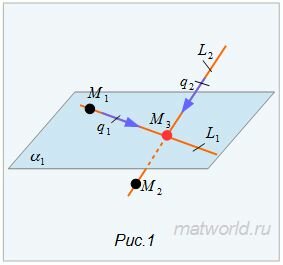 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
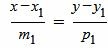 , , | (3) |
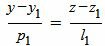 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
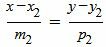 , , | (7) |
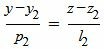 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
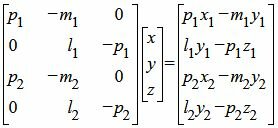 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
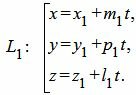 | (12) |
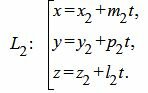 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
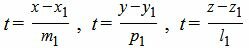 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
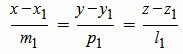 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
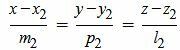 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
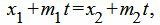 | (17) |
 | (18) |
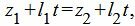 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
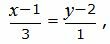 | (22) |
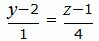 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
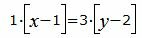 |
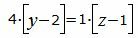 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
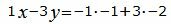 |
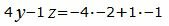 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
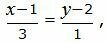 | (26) |
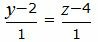 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
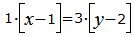 |
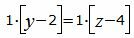 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
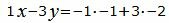 |
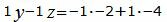 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
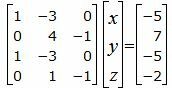 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
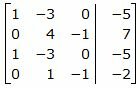 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
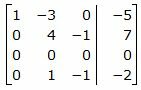 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
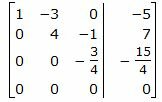 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
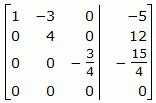 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
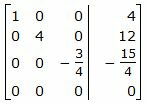 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
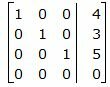 |
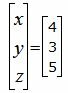 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
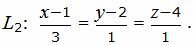 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
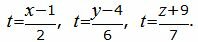 |
Из равентсв выше получим каноническое уравнение прямой:
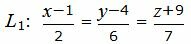 | (33) |
Представим уравнение (33) в виде двух уравнений:
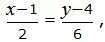 | (34) |
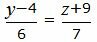 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
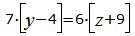 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
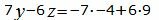 |
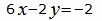 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
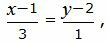 | (38) |
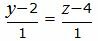 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
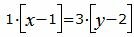 |
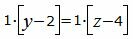 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
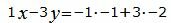 |
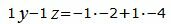 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
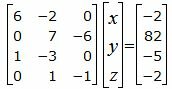 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
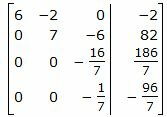 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
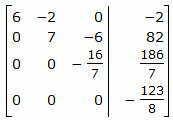 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
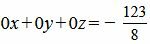 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
ПРЯМАЯ НА ПЛОСКОСТИ
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
Показать, при каких условиях прямые на плоскости параллельны, пересекаются, совпадают. Рассмотреть случаи, когда прямые заданы каноническими, общими или уравнениями с угловым коэффициентом. Научить находить косинус угла между пересекающимися прямыми и координаты точки их пересечения. Научить находить расстояние от точки до прямой на плоскости и расстояние между параллельными прямыми.
1) Школьники должны знать:
− условия, при которых прямые пересекаются, параллельны, совпадают, в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом;
− условия, при которых прямые перпендикулярны;
− формулу для нахождения расстояния от точки до прямой на плоскости;
− формулу для нахождения косинуса угла между пересекающимися прямыми в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом.
2) Школьники должны уметь:
− выяснять взаимное расположение прямых на плоскости;
− находить угол между прямыми на плоскости;
− находить расстояние от точки до прямой на плоскости;
− находить расстояние между параллельными прямыми на плоскости.
Взаимное расположение прямых на плоскости
Прямые на плоскости могут совпадать, пересекаться или быть параллельными.
1.Пусть на плоскости заданы общими уравнениями две прямые L1 и L2:
где 

а) совпадают, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой

б) параллельны, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.

в) пересекаются, если нормальные векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.

2.Пусть на плоскости заданы прямые L1 и L2 каноническими уравнениями:
а) совпадают, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой


б) параллельны, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.


в) пересекаются, если направляющие векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
3.Если прямые L1 и L2 заданы уравнениями с угловым коэффициентом
а) совпадают, если k1 = k2 и b1 = b2;
б) параллельны, если k1 = k2 и b1 ¹ b2;
в) пересекаются, если k1 ¹ k2.
Угол между прямыми на плоскости
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
1.Пусть на плоскости заданы прямые L1 и L2 общими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 на плоскости равен модулю косинуса угла между нормальными векторами этих прямых:
В случае если прямые L1 и L2 перпендикулярны, их нормальные векторы также перпендикулярны, а значит, скалярное произведение нормальных векторов должно быть равно нулю, т. е. 
2.Пусть прямые L1 и L2 заданы каноническими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 равен модулю косинуса угла между направляющими векторами этих прямых:
2. Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
Тогда тангенс наименьшего угла между прямыми L1 и L2 можно найти по формуле:

где k1 и k2 – угловые коэффициенты прямых L1 и L2.
Очевидно, что две прямые будут параллельны, если их угловые коэффициенты будут равны.
Итак, условие параллельности двух прямых:
Если две прямые перпендикулярны, т. е. угол φ = p/2, мы получим
Это будет иметь место, когда
Итак, условие перпендикулярности двух прямых:
Расстояние от точки до прямой на плоскости
Расстояние от точки до прямой, не содержащей эту точку, есть длина перпендикуляра, проведенного из этой точки на прямую.
Расстояние от точки до прямой можно вычислить:
1) Как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;
2) Используя координатно – векторный метод.
Пусть на плоскости заданы прямая L и точка M, не принадлежащая этой прямой

расстояние от точки М0(x0, y0) до прямой L.
Замечание. Расстояние между двумя параллельными прямыми на плоскости можно найти по последней формуле, если находить расстояние от любой точки, принадлежащей одной прямой, до другой прямой.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти угол между медианой и высотой, проведенными из вершины A.
Напишем уравнение высоты AH. Для любой точки M(x, y), лежащей на прямой AH, вектор 




Итак, уравнение высоты AH:
Напишем уравнение медианы, проведенной из вершины A. Найдем координаты точки D. Точка D − середина отрезка BC, значит, ее координаты можно найти как среднее арифметическое координат точек B и C. Координаты точек B(2, −1) и C(−3, 5), тогда координаты точки D:
Для любой точки N(x, y), лежащей на медиане AD, вектор 



Запишем условие пропорциональности координат:

По свойству пропорций получим:

Получили общее уравнение медианы AD:

Косинус наименьшего угла между прямыми равен модулю косинуса угла между нормальными векторами этих прямых.
Уравнение прямой AH: 




Ответ: 
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти расстояние от точки A до прямой BC.
Напишем уравнение прямой BC. Для любой точки N(x, y), лежащей на прямой BC, вектор 


Перемножив по свойству пропорций, перейдем к общему уравнению прямой:
Тогда общее уравнение прямой BC:

Точка A(4, 1) 



Ответ: расстояние от точки A до прямой BC равно 
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
L1: 
L2: 
Запишем координаты нормальных векторов прямых L1 и L2:
L1: 

L2: 

Найдем отношение координат нормальных векторов прямых:

Так как координаты нормальных векторов пропорциональны, то векторы 

Прямые параллельны так как

Расстояние между прямыми найдем, как расстояние от точки М1, лежащей на прямой L1, до прямой L2 по формуле:


Найдем координаты точки M1, принадлежащей прямой L1. Для этого одну из координат, например y0, примем равной нулю, тогда x0 = 4, значит, точка 
Ответ: прямые параллельны, расстояние между ними равно 
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
Найдем направляющие векторы прямых L1 и L2:

то координаты направляющих векторов не пропорциональны. Следовательно, прямые L1 и L2 пересекаются.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых.
Найдем координаты точки пересечения прямых L1 и L2. Для этого получим общие уравнения этих прямых.
Пусть точка М (x0, y0) − точка пересечения прямых L1 и L2. Тогда координаты точки М должны удовлетворять обоим уравнениям. Решим систему уравнений:
Следовательно, точка 
Ответ: прямые пересекаются, 

Задачи для усвоения пройденного материала.
1. Найти расстояние от точки А(−4, 1) до прямой, проходящей через точки B(1, −1), C(1, 5).
2. Выяснить взаимное расположение прямых 

3. Найти точку пересечения медиан треугольника, вершинами которого являются точки
4. Найти точку пересечения высот треугольника, вершинами которого являются точки
5. Написать уравнение прямой, проходящей через точку 

6. Найти угол между прямыми 
1. При каких значениях параметров прямые 

2. При каких значениях параметров прямые 

3. При каких значениях параметров прямые 

4. Как найти угол между пересекающимися прямыми,?
5. Как найти координаты точки пересечения прямых?
6. Как найти расстояние между параллельными прямыми?
7. При каких значениях параметров прямые 

🌟 Видео
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Взаимное расположение прямых на плоскости. 7 класс.Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

14. Угол между прямыми в пространствеСкачать

Уравнение прямой на плоскости. Решение задачСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

11 класс, 24 урок, Взаимное расположение сферы и прямойСкачать

Видеоурок "Угол между прямыми в пространстве"Скачать
Лекция 26. Взаимное расположение двух плоскостей.Скачать













































