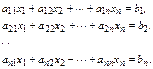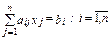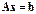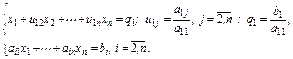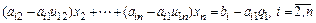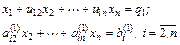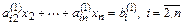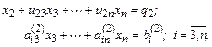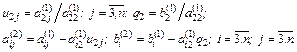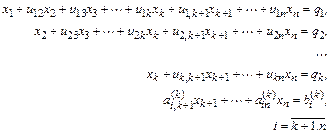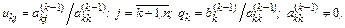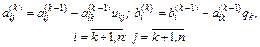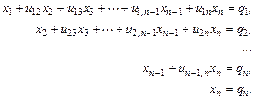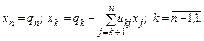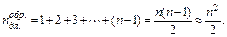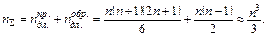Прямые и итерационные методы решения уравнений (5 видео)

Прямые и итерационные методы.

Часть 2. системЫ линейных

АлгебраичЕских уравнений

Лекция 2

ЦЕЛЬ ЛЕКЦИИ: Определить два класса численных методов (прямые и итерационные); показать, как строятся прямые методы Гаусса, LU-факторизации, Холесского; выполнить оценку их эффективности.

Постановка задачи.

Основная задача вычислительной алгебры – решение систем линейных алгебраических уравнений (СЛАУ)

В дальнейшем будем использовать запись этой системы в компактной форме:

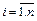
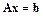
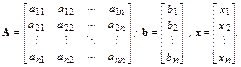( запись означает, что индекс i изменяется от 1 до n с шагом 1), или в векторном виде

Прямые и итерационные методы решения уравнений

где

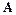
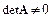
Предполагается, что матрица неособенная, т. е. , и решение единственно.

Прямые и итерационные методы.

Численные методы решения СЛАУ делятся на две большие группы: прямые и итерационные.

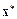
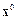
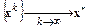
Прямые методы при отсутствии ошибок округления за конечное число арифметических операций позволяют получить точное решение . В итерационных методах задается начальное приближение и строится последовательность

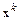
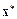
где k – номер итерации. В действительности итерационный процесс прекращается, как только становится достаточно близким к .

Имеется промежуточный класс методов, в которых решение ищется итерационно, однако для них заранее известно, какое число итераций необходимо выполнить, чтобы в отсутствии ошибок округления получить точное решение. На практике при вычислении приближенного решения число итераций в наиболее эффективных методах оказывается значительно меньшим, чем этого требует теория точного решения.

Какой класс методов лучше? Однозначно на этот вопрос ответить нельзя. Итерационные методы привлекательнее с точки зрения объема вычислений и требуемой памяти, когда решаются системы с матрицами высокой размерности. При небольших порядках системы используют прямые методы либо прямые методы в сочетании с итерационными методами.

Метод Гаусса.

В методе Гаусса линейная система

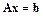
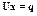
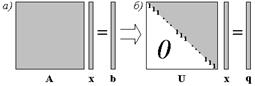решается в два этапа. На первом этапе система преобразуется к виду (см. рис. 2.1)

Рис. 2.1. Структура системы и портрет ее ненулевых элементов до (а) и после (б)

прямого хода Гаусса

где 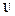– верхняя треугольная матрица с единичной диагональю (это так

называемый прямой ход Гаусса). На втором этапе (обратный ход Гаусса) решается система 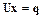. Рассмотрим эти этапы подробнее.

Прямой ход. Прямой ход Гаусса состоит из n шагов.

Первый шаг. Полагаем, что 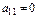и разделим на него первое уравнение. Перепишем систему с учетом этого преобразования:

Умножим первое уравнение на 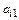и вычтем его из i-го уравнения преобразованной системы:

Обозначим 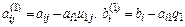. Получим

Второй шаг. На втором шаге из системы

исключается 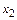аналогичным образом:

K-й шаг. Запишем общий вид преобразованной системы после k-го шага прямого хода Гаусса:

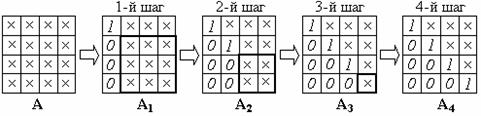
Проиллюстрируем, как меняется матрица системы в процессе прямого хода Гаусса на примере системы четвертого порядка (рис. 2.2; ненулевые элементы матрицы обозначены крестиками).

Рис. 2.2. Преобразование матрицы системы 4-го порядка на прямом ходе Гаусса

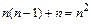
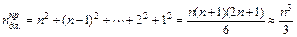
Оценим количество длинных операций (умножений и делений) на первом шаге прямого хода Гаусса. Преобразование первого уравнения требует n таких операций. Преобразование остальных n-1 уравнений – n(n-1) операций умножения и деления. Таким образом, первый шаг выполняется за длинных операций. Рассуждая по аналогии, нетрудно найти затраты на остальных n-1 шагах. Суммарные затраты прямого хода Гаусса определяются в итоге рядом

Последняя оценка имеет место для n>>1.

Обратный ход. Запишем систему, решаемую на обратном ходе, в координатном виде

Запись 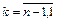означает, что индекс k изменяется от значения n-1 до 1 с шагом 1.

Требуемое число длинных операций на обратном ходе

Приближенная оценка справедлива для n>>1.

Общие затраты метода Гаусса:

Таким образом, при больших n основные затраты в методе Гаусса приходятся на прямой ход.

Дата добавления: 2015-11-24 ; просмотров: 2532 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Различие между прямыми и итерационными методами численного решения задач. Примеры

Все методы решения СЛАУ делятся на две группы – точные (прямые) и итерационные. Точные методы позволяют получить решение системы линейных уравнений за конечное число арифметических операций (метод Гаусса, метод квадратного корня, правило Крамара и т. д.). Использование итерационных методов дает возможность найти приближенное решение системы с заданной степенью точности (метод простой итерации, метод Зейделя, метод последовательной релаксации).

При решении СЛАУ возникает необходимость выбора того или иного метода, который позволит получить эффективный результат с использованием вычислительной техники. В этой ситуации актуализируется проблема сравнительного анализа прямых и итерационных методов решения СЛАУ.

Таким образом, критериями сравнения точных и итерационных методов решения СЛАУ с использованием вычислительной техники будут:

-область применения метода;

-временные затраты на решение;

Читайте также:

A) все перечисленное b) между сменами c) выходные дни d) праздничные дни e) для отдыха и приема пищи
I. Общее положение современной системы международных отношений.
II Всероссийский съезд Советов рабочих и солдатских депутатов и его важнейшие решения.
II. Международные факторы МРТ.
II. Основные теории по анализу международных отношений.
II. Рассмотрение заявления объекта туристской индустрии и представленных документов и принятие решения о проведении классификации
III. Причинная связь между общественно опасным действием (бездействием) и последствием
V. Основные направления развития международного сотрудничества
V. СССР и международные кризисы на мировой периферии.
V. СТАТУС МЕЖДУНАРОДНОЙ КОНВЕНЦИИ О БОРЬБЕ С ВЕРБОВКОЙ, ИСПОЛЬЗОВАНИЕМ, ФИНАНСИРОВАНИЕМ И ОБУЧЕНИЕМ НАЕМНИКОВ

-погрешность результата.

Прямой	Итерационный
1. неэффективны при реше-нии матриц большой размерности из-за выпол-нения чрезмерного числа арифметических операций;	1. область применения зависит от свойства сходимости;
1. приводит к необходимос-ти затраты большого количества времени при решении системы из-за кубической зависимость числа арифметических операций от размера матрицы	1. экономичны, в плане затраты машинного времени и использования оперативной памяти т. к. время решения, пропорционально квадрату размера матрицы.
1. нет сведений о точности полученного решения;	1. позволяют получить решение с любой заданной точностью.

25. два этапа решения численного решения трансцендентных уравнений

два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

Локализация корней. Для отделения корней уравнения (2.1) необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень.

Воспользовавшись этим критерием можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически, если удается построить график функции

Уточнение корней. На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) . Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину :

Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближенияк корню и вычислении по некоторой формуле последующих приближений , и т.д. Каждый такой шаг называется итерацией (от латинскогоiteratio – повторение), а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня , которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня

Дата добавления: 2015-02-16 ; просмотров: 43 | Нарушение авторских прав

Видео:Лекция 5, Итерационные методы решения систем линейных уравненийСкачать

Сравнение прямых и итерационных методов

1.3. Сравнение прямых и итерационных методов

Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и и итерационных методов. Для систем уравнений средней размерности чаще использют прямые методы.

Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограниченииий в доступной оперативной памяти ЭВМ или из-за необходимости выполнения черезмерно большого числа арифметических операций. Большие системы уравнений, возникающие в основном в приложениях, как правило являются разреженными. Методы исключения для систем с разреженным и матрицами неудобны, например, тем, что при их использовании большое число нулевых элементов превращается в ненулевые и матрица теряет свойство разреженности. В противоположность им при использованнии итерационных методов в ходе итерационного процесса матрица не меняется, и она, естественно, остается разреженной. Большая эффективность итерационных методов по сравнению с прямыми методами тесно связанна с возможностью существенного использования разреженности матриц.

Применение итерационных методов для качественного решения большой системы уравнений требует серьезного использования ее структуры, специальных знаний и определенного опыта.

2. Практическая часть

2.1 Программа решения систем линейных уравнений по методу Гаусса

2.1.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида

для n ≤ 10 по методу Гаусса.

2.1.2. Тестовый пример.

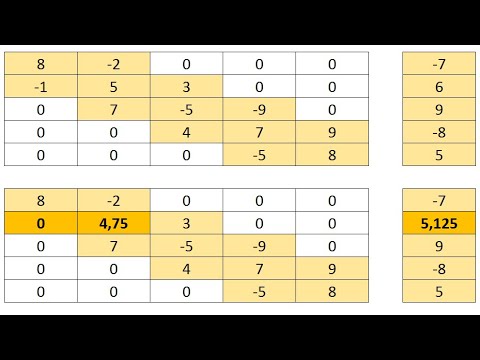
2.1.3. Описание алгоритма. В данной программе реализован метод Гаусса со схемой частичного выбора.

В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры ReadSystem в двумерный массив a и одномерный массив b вводится c клавиатуры расширенная матрица системы, после чего оба массива и переменная n передаются функции Gauss. В фукции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начинаяя с k-й строки. Номер строки, содержащей максимальный элемент сохраняеется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса. Далее вычисляется решение системы и помещается в массив x. Полученное решение выводится на экран при помощи вспомогательной процедуры WriteX.

2.1.4. Листинг программы и результаты работы

Matrix = Array[1..maxn, 1..maxn] of Data;

Vector = Array[1..maxn] of Data;

Procedure ReadSystem(n: Integer; var a: Matrix; var b: Vector);