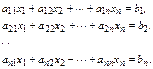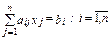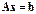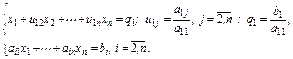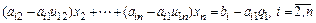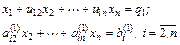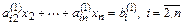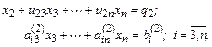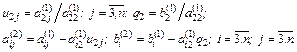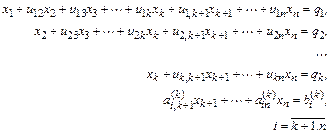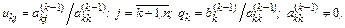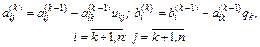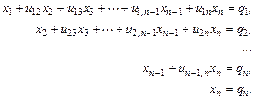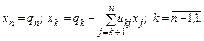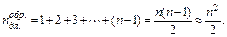Прямые и итерационные методы решения систем линейных уравнений

Все методы решения СЛАУ делятся на две группы – точные (прямые) и итерационные. Точные методы позволяют получить решение системы линейных уравнений за конечное число арифметических операций (метод Гаусса, метод квадратного корня, правило Крамара и т. д.). Использование итерационных методов дает возможность найти приближенное решение системы с заданной степенью точности (метод простой итерации, метод Зейделя, метод последовательной релаксации).

При решении СЛАУ возникает необходимость выбора того или иного метода, который позволит получить эффективный результат с использованием вычислительной техники. В этой ситуации актуализируется проблема сравнительного анализа прямых и итерационных методов решения СЛАУ.

Таким образом, критериями сравнения точных и итерационных методов решения СЛАУ с использованием вычислительной техники будут:

-область применения метода;

-временные затраты на решение;

два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

Локализация корней. Для отделения корней уравнения (2.1) необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень.

Воспользовавшись этим критерием можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически, если удается построить график функции

Уточнение корней. На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) . Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину :

.

Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближенияк корню и вычислении по некоторой формуле последующих приближений , и т.д. Каждый такой шаг называется итерацией (от латинскогоiteratio – повторение), а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня , которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня

Дата добавления: 2015-02-16 ; просмотров: 43 | Нарушение авторских прав

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Видео:Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Видео:Решение системы уравнений методом ГауссаСкачать

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .

Видео:Метод простой итерации Пример РешенияСкачать

Прямые и итерационные методы.

Часть 2. системЫ линейных

АлгебраичЕских уравнений

Лекция 2

ЦЕЛЬ ЛЕКЦИИ: Определить два класса численных методов (прямые и итерационные); показать, как строятся прямые методы Гаусса, LU-факторизации, Холесского; выполнить оценку их эффективности.

Постановка задачи.

Основная задача вычислительной алгебры – решение систем линейных алгебраических уравнений (СЛАУ)

В дальнейшем будем использовать запись этой системы в компактной форме:

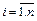
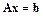
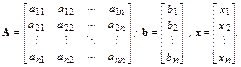( запись означает, что индекс i изменяется от 1 до n с шагом 1), или в векторном виде

,

где

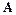
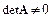
Предполагается, что матрица неособенная, т. е. , и решение единственно.

Прямые и итерационные методы.

Численные методы решения СЛАУ делятся на две большие группы: прямые и итерационные.

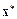
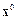
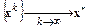
Прямые методы при отсутствии ошибок округления за конечное число арифметических операций позволяют получить точное решение . В итерационных методах задается начальное приближение и строится последовательность

,

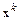
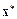
где k – номер итерации. В действительности итерационный процесс прекращается, как только становится достаточно близким к .

Имеется промежуточный класс методов, в которых решение ищется итерационно, однако для них заранее известно, какое число итераций необходимо выполнить, чтобы в отсутствии ошибок округления получить точное решение. На практике при вычислении приближенного решения число итераций в наиболее эффективных методах оказывается значительно меньшим, чем этого требует теория точного решения.

Какой класс методов лучше? Однозначно на этот вопрос ответить нельзя. Итерационные методы привлекательнее с точки зрения объема вычислений и требуемой памяти, когда решаются системы с матрицами высокой размерности. При небольших порядках системы используют прямые методы либо прямые методы в сочетании с итерационными методами.

Метод Гаусса.

В методе Гаусса линейная система

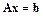
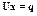
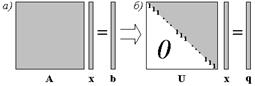решается в два этапа. На первом этапе система преобразуется к виду (см. рис. 2.1)

,

Рис. 2.1. Структура системы и портрет ее ненулевых элементов до (а) и после (б)

прямого хода Гаусса

где 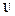– верхняя треугольная матрица с единичной диагональю (это так

называемый прямой ход Гаусса). На втором этапе (обратный ход Гаусса) решается система 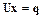. Рассмотрим эти этапы подробнее.

Прямой ход. Прямой ход Гаусса состоит из n шагов.

Первый шаг. Полагаем, что 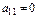и разделим на него первое уравнение. Перепишем систему с учетом этого преобразования:

Умножим первое уравнение на 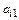и вычтем его из i-го уравнения преобразованной системы:

Обозначим 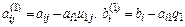. Получим

Второй шаг. На втором шаге из системы

исключается 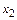аналогичным образом:

K-й шаг. Запишем общий вид преобразованной системы после k-го шага прямого хода Гаусса:

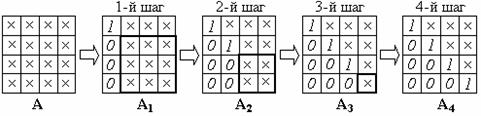
Проиллюстрируем, как меняется матрица системы в процессе прямого хода Гаусса на примере системы четвертого порядка (рис. 2.2; ненулевые элементы матрицы обозначены крестиками).

Рис. 2.2. Преобразование матрицы системы 4-го порядка на прямом ходе Гаусса

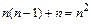
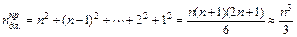
Оценим количество длинных операций (умножений и делений) на первом шаге прямого хода Гаусса. Преобразование первого уравнения требует n таких операций. Преобразование остальных n-1 уравнений – n(n-1) операций умножения и деления. Таким образом, первый шаг выполняется за длинных операций. Рассуждая по аналогии, нетрудно найти затраты на остальных n-1 шагах. Суммарные затраты прямого хода Гаусса определяются в итоге рядом

.

Последняя оценка имеет место для n>>1.

Обратный ход. Запишем систему, решаемую на обратном ходе, в координатном виде

Запись 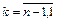означает, что индекс k изменяется от значения n-1 до 1 с шагом 1.

Требуемое число длинных операций на обратном ходе

Приближенная оценка справедлива для n>>1.

Общие затраты метода Гаусса:

Таким образом, при больших n основные затраты в методе Гаусса приходятся на прямой ход.

Дата добавления: 2015-11-24 ; просмотров: 2579 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

📸 Видео

Лекция 5, Итерационные методы решения систем линейных уравненийСкачать

Матричный метод решения систем уравненийСкачать

Вычислительная математика 3 Итерационные методы решения СЛАУСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

Лекция 4, Прямые методы решения систем линейных уравненийСкачать

6 способов в одном видеоСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать

Решение системы уравнений методом Крамера.Скачать

Вычислительная математика. Лекция 3. Итерационные методы решения систем уравненийСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Кобельков Г. М. - Численные методы. Часть 1. Лекции - Итерационные методы решения линейных уравненийСкачать

Решение системы линейных уравнений методом ГауссаСкачать