В 11-ом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.
Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.
Задание 11 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.
Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.
- Теория к заданию №11
- Разбор типовых вариантов задания №11 ОГЭ по математике
- Первый вариант задания (параболы)
- Второй вариант задания (гиперболы)
- Третий вариант задания (линейный график)
- Какая из следующих прямых отсутствует на рисунке 1? 1) у = 2х + 3 2) у = 2х — 3 3) у = -2х + 3 4) у = -2х — 3
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Ваш браузер не поддерживается
- Экзамен по алгебре в 9-м классе «Функции»
- 🌟 Видео
Теория к заданию №11
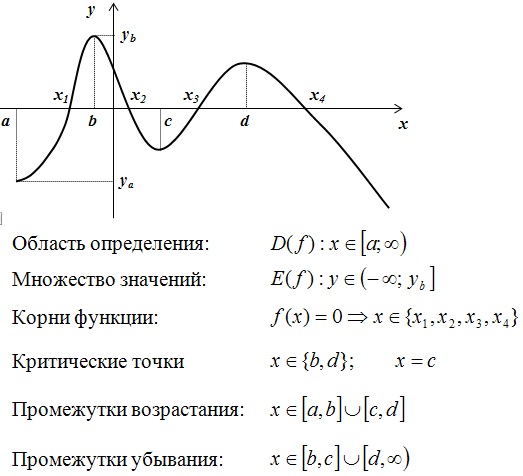
Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.
На произвольном примере ознакомимся с исследованием функции:
- область определения и множество значений
- корни и критические точки
- промежутки возрастания убывания
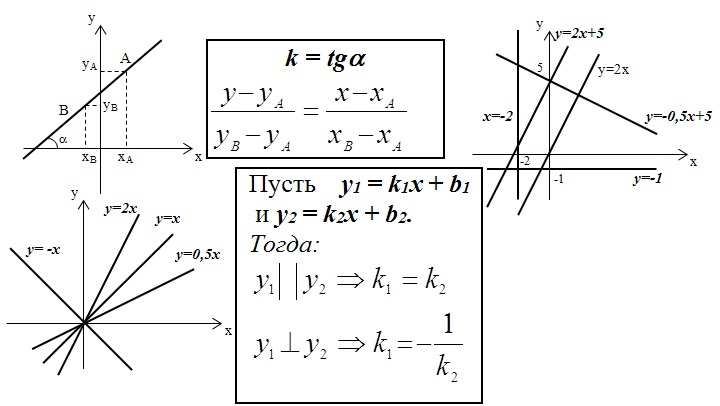
Теперь рассмотрим данный материал на линейной функции:
y = kx + b
где k – угловой коэффициент, b – свободный член
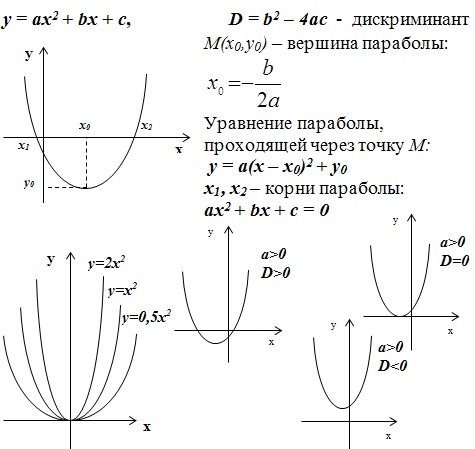
Рассмотрим случай квадратичной функции:
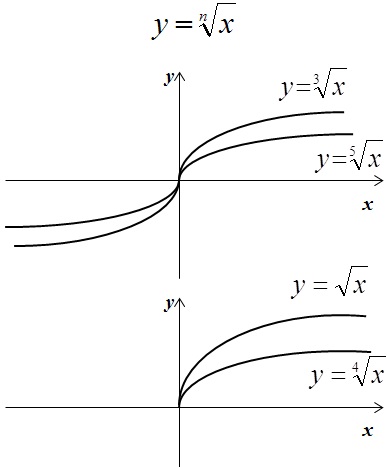
Также вспомним, что такое коренная функция и модуль:
Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.
Разбор типовых вариантов задания №11 ОГЭ по математике
Первый вариант задания (параболы)
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
В) a > 0, c 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
Второй вариант задания (гиперболы)
Установите соответствие между функциями и их графиками.
Решение:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Третий вариант задания (линейный график)
Установите соответствие между функциями и их графиками.
Видео:ОГЭ 2022. Задание 11. Подробный разбор. Функция прямая. Как отличать.Скачать
Какая из следующих прямых отсутствует на рисунке 1? 1) у = 2х + 3 2) у = 2х — 3 3) у = -2х + 3 4) у = -2х — 3
Видео:Как построить график функции без таблицыСкачать
Ваш ответ
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
решение вопроса
Видео:Как построить график линейной функции.Скачать
Похожие вопросы
- Все категории
- экономические 43,427
- гуманитарные 33,634
- юридические 17,906
- школьный раздел 608,218
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать
Ваш браузер не поддерживается
Рнтернет-сервис Студворк построен РЅР° передовых, современных технологиях Рё РЅРµ поддерживает старые браузеры. Для просмотра сайта загрузите Рё установите любой РёР· следующих браузеров:
Видео:Уравнение прямой по графику. ПримерыСкачать
Экзамен по алгебре в 9-м классе «Функции»
Разделы: Математика
№1. Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках график функции
Построим график данной функции. Прямые y=2x+1 и
y=2x-3 параллельны ,т.к. у них одинаковый угловой коэффициент , равный 2. Прямая y= — 1 параллельна оси абсцисс.
| y=2x+1, | y=2x — 3. |
| y(0)= 1, y(-1)= -1, | y(0)= — 3, y(1)= — 1. |
Прямая n задана уравнением y=2x. Для нахождения уравнения прямой l необходимо подставить координаты точки А(-1; -1) в уравнение y=kx.
-1=(-1)k. Отсюда k=1. Уравнение прямой l имеет вид y=kx.
Для того чтобы искомая прямая m пересекала график данной функции в трех различных точках (рис.1), она должна располагаться между прямыми n и l. При этом 1
№2 Постройте график функции y = f(x), где
При каких значениях m прямая y = m имеет с графиком этой функции три общие точки?
1. Графиком функции 
является парабола.
а) Ветви параболы направлены вниз.
б) 
(–1;2) – координаты вершины параболы.
– координаты точек пересечения параболы и оси Оx (оси абсцисс).
(0;1) – координаты точки пересечения параболы и оси Оy(оси ординат).
2. Графиком функции 
является парабола.
а) Ветви параболы направлены вверх.
б) 
– координаты точки вершины параболы.
– координаты точек пересечения параболы и оси Оx(оси абсцисс).
(0; – 5) – координаты точки пересечения параболы и оси Оy(оси ординат).
Найдём дополнительные точки для точного построения графика функции 
:
Найдём дополнительные точки для точного построения графика функции 
:
График данной функции (рис.2) только в трёх точках пересекают прямые
№ 3. Постройте график функции y= ¦ (x) , где
При каких значениях m прямая y = m имеет с графиком этой функции две общие точки?
Построим график данной функции. Для этого проведем исследования.
1. Графиком функции y= — x 
— 4x – 3 является парабола, ветви которой направлены вниз. Найдем координаты вершины параболы:
x
= 
= — 2, y
= y( — 2 ) = -4+8-3= 1.
Определим точки пересечения параболы с осями координат:
x=0, y = -3; y=0, x
= — 3, x
= — 1. y (-4)= -16+16-3= — 3.
2. Графиком функции y= x + 1 является прямая.
y ( — 1 )= 0 , y (1) = 2.
3. Графиком функции y= 
является гипербола. В нашем случае достаточно построить одну ветвь гиперболы , т.к. нам нужна часть гиперболы при x > 1. y(1) = 2, y(2)= 1, y(4)=0,5.
График данной функции (рис.3) только в двух точках пересекает прямая y=0 и прямые y=m при 1
№ 4. Постройте график функции y = 
.
При каких значениях x выполняется неравенство y ? 3 ?
Найдем область определения функции:
2x — x
0, x (2 – x) 
0, x 
0, x 
2.
Преобразуем выражение, задающее функцию:
y = 
= — (x + 1),
x
, x
=2, x
= — 1.
Построим прямую y= -(x + 1)= — x – 1 и “ выколем ” на ней точки, абсциссы которых равны 0 и 2 (рис.4).
y(- 4) = 3, y(0) = -1, y( 2) = -3.
— 4
x 2.
x 2.
Ответ: [- 4; 0) E (0; 2) E (2; + ? ).
№ 5. Постройте график функции y= 
.
1. Найдем область определения данной функции:
x
+6x+8 
0 ,
x+6x+8 =0, x
= -4, x
= -2.
Значит, областью определения является множество всех действительных чисел , кроме – 4 и – 2.
2. Для разложения числителя на множители решим уравнения :
а) x
+7x+12=0, б) x
+3x+2=0,
x
= — 3, x
= — 4 ; x
= — 2, x
= -1.
3. Упростим данную функцию:
y= 
= (x+3)(x+1)=x
+4x+3 .
4.Исследуем полученную квадратичную функцию: графиком функции y = x+4x+3 является парабола , ветви которой направлены вверх, вершина её имеет координаты x
= — 2, y
= -1; точки пересечения с осями координат — x=0, y=3; y=0 при x=-3 и x=-1.
5. Построим параболу и “выколем” на ней точки, абсциссы которых равны — 4 и – 2, поскольку при этих значениях переменной исходная функция не определена (рис.5).
№ 6. Постройте график функции y= 
.
1. Найдем область определения данной функции:
2. Упростим данную функцию:
y== 
=
=x+1.
3. Построим прямую y=x+1 на промежутках (- 1; — 1) и (1; + 
) (рис.6).
№ 7. Задайте аналитически функцию, график которой изображен на рисунке 7.
Ломаная состоит из двух звеньев, одно из них является графиком линейной функции y=kx+b при x 
2, а другое – графиком линейной функции при x > 2.
В каждом случае необходимо найти k и b.
Для этого необходимо на каждом из звеньев выбрать по две точки, подставить их координаты в уравнение линейной функции и решить две получившиеся системы уравнений относительно k и b.
1)На левом звене возьмем точки с координатами (-2;0) и (2; -6).
решая эту систему получаем b= — 3, k = — 1,5.
Получим уравнение прямой y= -1,5 x–3 при x 
2.
2) На второй части ломаной возьмем точки с координатами (2; — 6) и (4;0).
вычитая из второго уравнения первое, получим k=3, а b= — 12.
Получим уравнение прямой y= 3x – 12 при x > 2.
Зададим теперь заданную графически функцию аналитически:
🌟 Видео
Прямая пропорциональность и её график. Алгебра, 7 классСкачать
Построить график ЛИНЕЙНОЙ функции и найти:Скачать
9 класс, 7 урок, Уравнение прямойСкачать
График функции y=x² (y=аx).Скачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Линейная функция и ее график. 7 класс.Скачать
Линейная функция. Нахождение формулы линейной функцииСкачать
Параллельные прямые | Математика | TutorOnlineСкачать
Функция f(x)=asinx+b. Найти a.Скачать
Решите уравнение sin п(4x-3)/4 = 1. В ответе напишите наибольший отрицательный корень.Скачать
10 класс, 16 урок, Функции y=sinx, y=cosx, их свойства и графикиСкачать
Задание 8 | ВПР-7 2024 Математика | Нахождение формулы линейной функцииСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Уравнение окружности (1)Скачать
