Прямая с уравнением отсекает от осей координат прямоугольный треугольник найти длину его гипотенузы

Условие

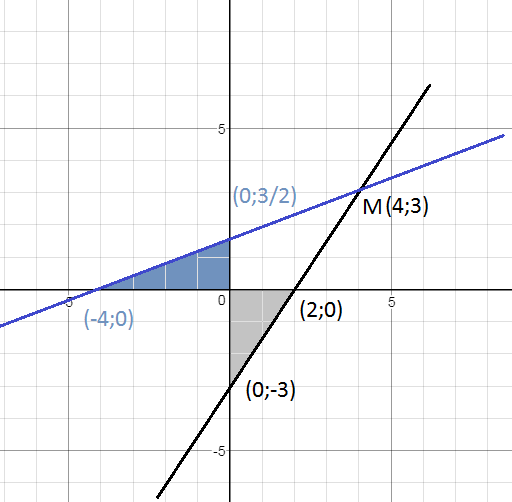
4.2.36. Через точку M(4; 3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Найти точки пересечения этой прямой с осями координат.

Решение

Пусть прямая проходит через точки (0;b) и (a;0)
Составим уравнение прямой:
(x-0)/(а-0)=(y-b)/(0-b)
-bx=ay-ab
ay+bx-ab=0
Подставим координаты точки М (4;3) в уравнение
а*3+b*4-ab=0

По условию прямая отсекает от координатного угла треугольник, площадь которого равна 3.
Треугольник прямоугольный.
Его катеты |а| и |b|

S = (1/2)|a|*|b| ⇒ 3 = (1/2)|ab| ⇒ |ab| = 6

⇒ ab = 6 или ab= — 6

3a+4b-6=0 ⇒ b = (6-3a)/4 и подставим в первое уравнение

a*(6-3a)/4 = 6
3а^2 — 6a +24=0
a^2-2a+8=0
D=4-32

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

ВЫЧИСЛИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА, отсекаемого от координатных осей касательной к кривой f(x) = 2√x — 3 — 5 / 2, проведенной параллельной прямой y = 7 + 1 / 2x?

Геометрия | 10 — 11 классы

ВЫЧИСЛИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА, отсекаемого от координатных осей касательной к кривой f(x) = 2√x — 3 — 5 / 2, проведенной параллельной прямой y = 7 + 1 / 2x.

Касательная параллельна прямой, т е производная функции = 1 / 2, х = 3, 25 уравнение касательной у = — 1.

Точки пересечения с осями : Оу — х = 0 у = — 3, 125 ; Ох — у = 0, х = 6, 25.

Площадь = 6, 25 * 3, 125 / 2 = , 765625.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Катеты прямоугольного треугольника равны 6 и 8?

Катеты прямоугольного треугольника равны 6 и 8.

Через середину его гипотенузы проведены две прямы, параллельные катетам.

Найдите площадь четырехугольника, отсекаемого данными прямыми от треугольника.

Видео:Видеоурок "Уравнение прямой в отрезках"Скачать

Катеты прямоугольного треугольника равны 6м и 8м?

Катеты прямоугольного треугольника равны 6м и 8м.

Через середину его гипотенузы проведены две прямые, параллельные катетам.

Найдите площадь четырёхуогольника , отсекаемого данными прямыми от треугольника.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Решить задачу?

Высота треугольника равна 2√2.

Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого равна половине площади данного треугольника.

Найти высоту отсеченного треугольника.

Видео:Длина отрезкаСкачать

Прямая проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 28, отсекает треугольник, периметр которого равен 57?

Прямая проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 28, отсекает треугольник, периметр которого равен 57.

Найдите периметр трапеции.

Видео:Уравнения стороны треугольника и медианыСкачать

Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части?

Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части.

Периметр большего треугольника равен 27 см.

Найти периметр меньшего треугольника.

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Прямая проходит через точки А(1 ; — 1) и B( — 3 ; 2)?

Прямая проходит через точки А(1 ; — 1) и B( — 3 ; 2).

Найдите площадь треугольника, отсекаемого этой прямой от осей координат.

Видео:найти уравнения биссектрис углов между прямымиСкачать

Записать уравнение прямой, проходящей через точку H (2 ; — 5) и отсекающей на координатных осях отрезки равной длины?

Записать уравнение прямой, проходящей через точку H (2 ; — 5) и отсекающей на координатных осях отрезки равной длины.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 34, отсекает треугольник, периметр которого равен 69?

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 34, отсекает треугольник, периметр которого равен 69.

Найдите периметр трапеции.

Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Найти уравнение касательной и кривой y = x ^ 3 параллельных прямой y = 3x + 1, 5?

Найти уравнение касательной и кривой y = x ^ 3 параллельных прямой y = 3x + 1, 5.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Прямая отсекает от четвёртой координатной четверти прямоугольный треугольник с катетами длины 5?

Прямая отсекает от четвёртой координатной четверти прямоугольный треугольник с катетами длины 5.

Запишите уравнение такой прямой.

На этой странице вы найдете ответ на вопрос ВЫЧИСЛИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА, отсекаемого от координатных осей касательной к кривой f(x) = 2√x — 3 — 5 / 2, проведенной параллельной прямой y = 7 + 1 / 2x?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Пусть наименьший угол равен 2х, тогда остальные угол равен 52х и 11х, сумма углов треугольников равна 180 градусов. Составим и решим уравнение. 2х + 52х + 11х = 180° 65х = 180° х = 180° : 65 х = 2, 7 2х = 2 * 2, 7 = 5, 4° 11х = 11 * 2, 7 = 29, 7° 5..

Не гарантирую что это самое удобное и быстроерассуждение, однако оно решает поставленную задачу. Смотри на фото.

ADC + CDB = 180° 4 + 5 = 9 (частей) 180° : 9 = 20° (в одной части) 20° * 4 = 80° (CDB) 20° * 5 = 100° (ADC).

46 + 46 = 92 град сумма двух углов 360 — 92 = 268 град сумма двух углов 268 : 1 = 134 град второй угол, а первый известен и = 46 град третий угол равен первому, в четвертый второму 2)186 : 2 = 93 град первый угол 360 — 186 = 174 град сумма других дву..

На два делятся — 42, 702, 1110, на три делятся — 63, 1005, 1110 на 5 делятся — 415, 1005, 1110 на 9 делятся — 63, 702 на 10 делятся — 1110.

( — 6 + ( — 15) ; — 10 + ( — 3) = ( — 21 ; — 13).

Ответ : Вектор k — искомый вектор (смотри рисунок в приложении). Объяснение : Умножение (деление) вектора на число — умножение (деление) модуля вектора (его длину) на это число. Правило : Для получения вектора разности (c) = (a — b) начала векторов..

Пусть FD пересекается HE = O, трг EDO — р / б т. К углы равны по условию = > EO = OD ; трг AFE = трг HDC (угол A = углу C, AE = DC, AF = CH т. К трг р / б) по 1 признаку = > FE = HD трг EHC = тргAFD (1 = 2, 3 = 4, AF = HC) по 2 признаку = > угол H ..

1. ) 10 * 4 = 40 2. )40 — 12 = 32.

Свойства равнобедренного треугольника и признаки параллельности прямых.

Видео:ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

Расчет гипотенузы треугольника

Гипотенуза треугольника — это самая длинная сторона прямоугольного треугольника, лежащая против его прямого угла.

Формула расчета гипотенузы:

c = √(a 2 + b 2 ), где

a — катет;
b — катет;
c — гипотенуза.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета гипотенузы прямоугольного треугольника, если известны его катеты. С помощью этой программы вы в один клик сможете рассчитать гипотенузу треугольника.

🔍 Видео

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Координатная прямая. Противоположные числа. 6 класс.Скачать

Уравнение прямой.Скачать

Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

68. Уравнение прямой в отрезках на осяхСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать