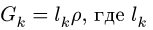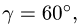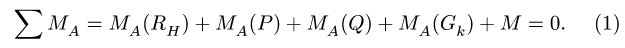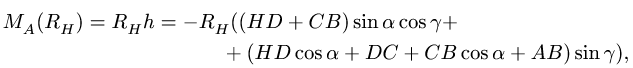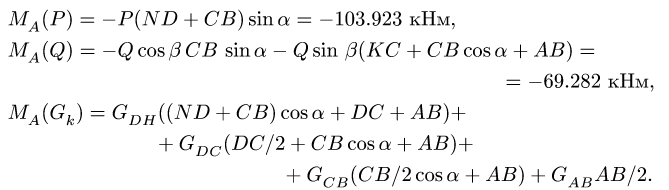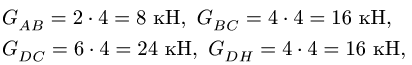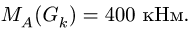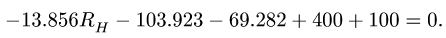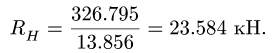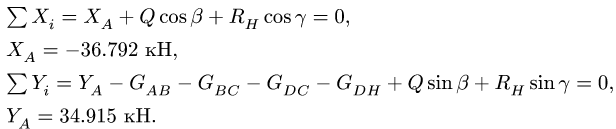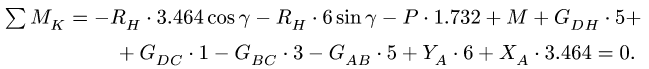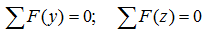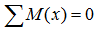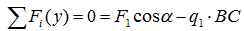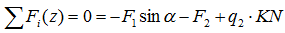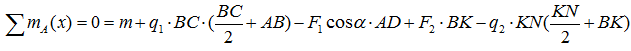Провести анализ системы сил и записать уравнения равновесия для рамы (8 видео)

Равновесие тяжелой рамы в теоретической механике

Равновесие тяжелой рамы:

ПОСТАНОВКА ЗАДАЧИ. Тяжелая однородная рама расположена в вертикальной плоскости и опирается на неподвижный шарнир и наклонный невесомый стержень. К раме приложены внешние сосредоточенные силы и моменты. Учитывая погонный вес рамы, найти реакции опор.

1.Согласно аксиоме о связях, освобождаем раму от связей. Действие опор заменяем их реакциями. Выбираем систему координат. В неподвижном шарнире имеются две неизвестные составляющие реакции (горизонтальная и вертикальная), а в невесомом опорном стержне — одна неизвестная реакция, направленная вдоль стержня. Все наклонные силы раскладываем на составляющие вдоль осей координат.

2. К центру каждого участка рамы прикладываем его вес, вычисленный по формуле

3. Составляем уравнение моментов всех сил, действующих на раму, относительно неподвижного шарнира. Определяем из этого уравнения реакцию опорного стержня.

4.Составляем уравнения проекций всех сил на оси х и у. Из этих уравнений определяем составляющие реакции неподвижного шарнира (горизонтальную и вертикальную).

5. Выполняем проверку решения, составляя уравнение моментов относительно какой-либо точки, не лежащей на линиях действия искомых реакций.

Задача:

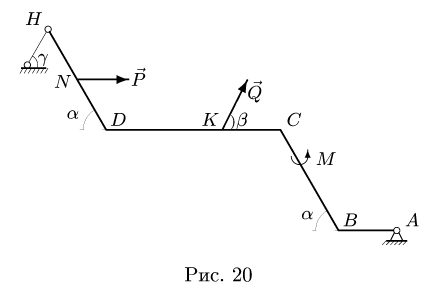
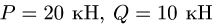
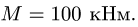
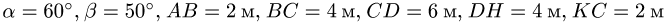
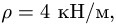
Тяжелая однородная рама расположена в вертикальной плоскости и опирается на неподвижный шарнир А и наклонный невесомый стержень Н. К раме приложены внешние сосредоточенные силы и момент Дано: (рис.20).Учитывая погонный вес рамы найти реакции опор.

Решение

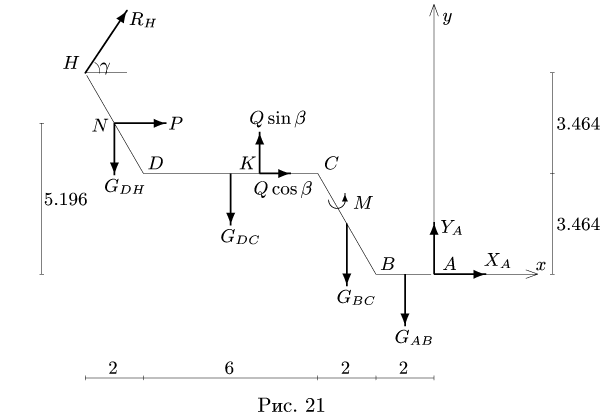
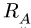
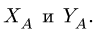
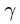
1.Освобождаем раму от связей. Действие опор заменяем их реакциями (рис. 21). Выбираем систему координат с началом в точке А. В неподвижном шарнире А реакция имеет две неизвестные компоненты Невесомый опорный стержень в шарнире Н заменяем на его реакцию, направленную по стержню (т.е. под углом к горизонту).

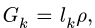
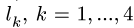
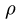
2.К центру каждого участка рамы (всего четыре прямолинейных участка) прикладываем его вес, вычисленный по формуле где--длины отрезков рамы АВ, ВС, CD и DH, — погонный вес рамы.

3. Составляем уравнение моментов относительно шарнира А, выделяя в нем для удобства счета отдельные слагаемые:

Момент 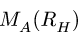реакции опоры

где h — плечо реакции 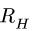взятое со знаком момента.

Моменты сил Р и Q и момент 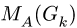сил тяжести участков:

Вычисляя величины сил тяжести участков

получаем

В итоге уравнение моментов (1) принимает вид

Отсюда находим реакцию стержня

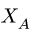
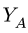
4. Реакции и определяем из уравнений проекций:

Ответы заносим в таблицу. Моменты — в кНм, силы — в кН.

5. Проверка. Составляем сумму моментов всех сил, действующих на раму, включая найденные реакции опор, относительно произвольной точки, например, К. Этот выбор оправдывается тем, что в уравнение моментов войдут все найденные реакции, а известная сила Q не войдет (ее проверять не требуется), и уравнение будет на два слагаемых короче

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

Расчет составной конструкции
Момент силы относительно оси
Равновесие вала
Определение усилий в стержнях, поддерживающих плиту
Плоскопараллельное движение тела
Определение передаточных отношений различных передач
Задачи на поступательное движение тела
Задачи на вращательное движение тела

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание

iSopromat.ru
Уравнения равновесия
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ О РАВНОВЕСИИ ПЛОСКОЙ СИСТЕМЫ СИЛ
🔥 Видео

Видео:Определение реакций опор простой рамыСкачать

iSopromat.ru

Рассмотрим порядок составления уравнений равновесия для плоской системы нагрузок, например в раме.

В сопротивлении материалов при определении опорных реакций и внутренних силовых факторов для плоской схемы нагружения, исходя из условий равновесия, можно составить только три уравнения статики:

Равенство нулю суммы проекций всех сил на вертикальную и горизонтальную оси

Частный случай составления уравнений статики для балки при плоском поперечном изгибе рассмотрен здесь.

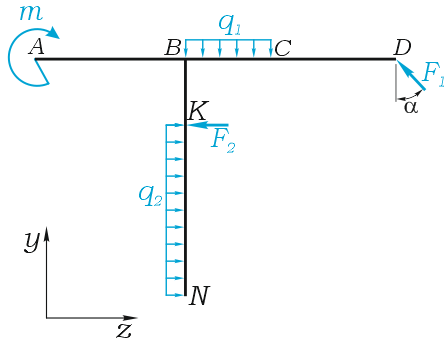
Рассмотрим пример действия плоской системы сил, удерживающего Т-образную раму в равновесии.

Видео:Определение реакций опор простой рамыСкачать

Уравнения равновесия

Сумма проекций всех сил и нагрузок на ось Y (с учетом соответствующего правила знаков):

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции на ось Z:

Сумма моментов всех нагрузок, например, относительно точки A (с учетом правила знаков для моментов):

Порядок определения момента распределенной нагрузки показан здесь.

Совместное решение системы трех полученных уравнений позволяет определить величину и направление до трех неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

МЕТОДИКА РЕШЕНИЯ ЗАДАЧ О РАВНОВЕСИИ ПЛОСКОЙ СИСТЕМЫ СИЛ

Для решения задач на равновесие плоской системы сил можно пользоваться любой формой уравнений равновесия. Целесообразно составлять уравнения так, чтобы они были решены наиболее просто и быстро. Каждое из уравнений равновесия должно содержать одну неизвестную. К такой системе можно прийти при соответствующем выборе координатных осей и центров моментов.

В качестве центров моментов рекомендуется выбирать точку опоры, так как уравнение моментов относительно этой точки содержит одну неизвестную. Направление координатных осей хиу следует выбирать так, чтобы одна из осей была перпендикулярна некоторым неизвестным силам, а при проектировании этих сил на эту ось в уравнение они не войдут. (Ось х следует направлять вдоль балки, а ось у — из крайней левой точки балки.) Определение неизвестных величин лучше начинать с уравнений проекций, а затем переходить к уравнениям моментов. При этом можно избежать совместного решения уравнений и уменьшить вероятность ошибок. Все аксиомы и положения статики устанавливаются для так называемых сосредоточенных сил, т.е. для сил, приложенных к тем или иным точкам твердого тела. На практике же часто приходится иметь дело с силами, распределенными вдоль данной длины по некоторому закону. При решении задач статики такую систему сил надо заменить ее равнодействующей.

Если в состав плоской системы сил, действующих на находящееся в равновесии тело, входит пара сил, то, составляя уравнения равновесия, надо иметь в виду, что алгебраическая сумма проекций сил любой пары на любую ось равна нулю (так как пара всегда представляет собой систему двух равных по модулю, параллельных и противоположно направленных сил).

Многие задачи статики заключаются в определении реакций связей, в частности реакций опор различного рода балочных систем, ферм и т.п.

Пример 1. На горизонтальную балку АВ, заделанную в стену в точке В (рис. 1.4.6, а), действует сила F = 40 кН в точке А под углом 30° к вертикали и момент М— 30 кНм. На участке АС действует равномерно распределенная нагрузка интенсивностью q = 25 кН/м. Определить реакции в заделке.

Решение. Заменим равномерно распределенную нагрузку равнодействующей F, приложенной в середине АС: Fq = qAC = 25 • 4 = = 100 кН.

Рассмотрим равновесие балки. К ней приложены активные силы F, F_q, М. Освободимся от связи-заделки, заменив ее вертикальной реакцией V_B, горизонтальной реакцией Н_в и моментом М_в. Получим силовую схему (рис. 1.4.6, б). Направим оси координат таким образом, что начало координат будет в точке А, ось х — горизонталь, совпадает с балкой АВ, ось у — вертикаль. Разложим силу F на горизонталь и вертикаль:

Составляем уравнения равновесия по первой форме:

Знак (—) означает, что Н_в направлена в противоположную сторону;

F_q+V_B = 0, V_B = F + F = 34,64 + 100 = = 134,64 кН;

3) 1М_В = 0, -F -6-F -4-М+М_в = 0, M_B = F -6 + F -4 + М= = 34,64 -6+ 100-4 + 30 = 207,84 + 400 + 30 = 637,84 кН.

Проверка. Алгебраическая сумма моментов относительно точки Сдолжна быть равна нулю, ХМ_С = 0. —F • 2 — F‘-4 — М— V_B 2 + + м_в = -100 • 2 — 34,64 -4 — 30 — 134,64 • 2 + 637,84 = 0. Реакции найдены верно.

Пример 2. Определить опорные реакции балки АВ, нагруженной парой сил с моментом М— 18 кНм и распределенной нагрузкой интенсивностью q = 2 кН/м (рис. 1.4.7, а).

Решение. Заменяем равномерно распределенную нагрузку равнодействующей F. приложенной в середине участка СВ. F_q = qCВ = = 2 • 6 = 12 кН. Рассматриваем равновесие балки. К ней приложены активные силовые факторы: М, F_q. Освободимся от связей, заменив их реакциями V_A, Н_А, V_B. Составляем силовую схему (рис. 1.4.7, б).

Направляем оси координат таким образом, что начало координат будет в точке А, ось х направлена вдоль балки АВ, ось у — вертикальна. Составим уравнения равновесия.

Воспользуемся второй формой уравнений равновесия:

CR M + F-3 1Я + 12-3

Проверим правильность определения реакций из уравнения ЪР_у = 0:

Задачи для самостоятельного решения

Определить реакции в опорах для балок, приведенных на рис. 1.4.8.

Вопросы для самопроверки

1. Что называется моментом силы относительно данной точки?
2. Как выбирается знак момента?
3. Что такое плечо силы?
4. Изменится ли момент силы относительно данной точки при переносе силы по линии ее действия?
5. В каком случае момент силы относительно точки равен нулю?
6. Что значит привести силу к данному центру?
7. Что называется присоединенной парой?
8. Что называется главным вектором и главным моментом плоской системы сил и как они определяются?
9. Чем отличается главный вектор от равнодействующей данной системы?

10. Изменится ли главный момент и главный вектор при перенесении центра приведения?
11. В чем смысл теоремы Вариньона?
12. Сформулируйте условия равновесия плоской системы произвольно расположенных сил, напишите уравнения равновесия для такой системы сил (три вида).
13. Как с помощью теоремы Вариньона найти точку, через которую проходит линия действия равнодействующей плоской системы параллельных сил?
14. Напишите уравнения равновесия для плоской системы параллельных сил (два вида).