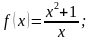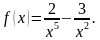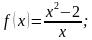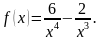Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.
- Просмотр содержимого документа «Контрольная работа № 7 по теме «Производная. Уравнение касательной» (10 класс, Мерзляк А.Г. и др.)»
- Тестовые задания по теме: «Касательная к графику функции»
- Урок алгебры в 10 классе по теме «Уравнение касательной к графику функции»
- Выберите документ из архива для просмотра:
- 🎬 Видео
Просмотр содержимого документа
«Контрольная работа № 7 по теме «Производная. Уравнение касательной» (10 класс, Мерзляк А.Г. и др.)»
Контрольная работа № 7 по теме «Производная. Уравнение касательной»
1. Найдите производную функции:
1) 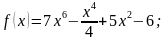
2) 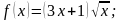
2. Составьте уравнение касательной к графику функции 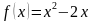
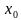
3. Материальная точка движется по координатной прямой по закону 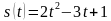
4. Найдите производную данной функции и вычислите её значение в точке x0:
1) 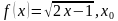
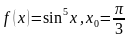
5. Найдите абсциссу точки графика функции 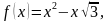
6. Найдите уравнение касательной к графику функции 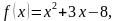
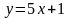
1. Найдите производную функции:
1) 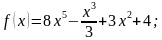
2) 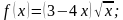
2. Составьте уравнение касательной к графику функции 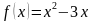
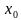
3. Материальная точка движется по координатной прямой по закону 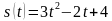
4. Найдите производную данной функции и вычислите её значение в точке x0:
1) 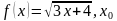
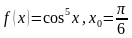
5. Найдите абсциссу точки графика функции 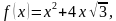
6. Найдите уравнение касательной к графику функции 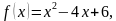
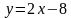
1. Найдите производную функции:
1) 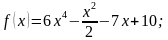
2. Составьте уравнение касательной к графику функции в точке с абсциссой 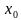
3. Материальная точка движется по координатной прямой по закону (перемещение s измеряется в метрах, время t — в секундах). Найдите скорость её движения в момент времени t0 = 5 с.
4. Найдите производную данной функции и вычислите её значение в точке x0:
5. Найдите абсциссу точки графика функции в которой проведённая к нему касательная образует с положительным направлением оси абсцисс угол 45°.
6. Найдите уравнение касательной к графику функции если эта касательная параллельна прямой .
1. Найдите производную функции:
2. Составьте уравнение касательной к графику функции в точке с абсциссой 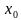
3. Материальная точка движется по координатной прямой по закону (перемещение s измеряется в метрах, время t — в секундах). Найдите скорость её движения в момент времени t0 = 4 с.
4. Найдите производную данной функции и вычислите её значение в точке x0:
5. Найдите абсциссу точки графика функции в которой проведённая к нему касательная образует с положительным направлением оси абсцисс угол 135°.
6. Найдите уравнение касательной к графику функции если эта касательная параллельна прямой .
Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Тестовые задания по теме: «Касательная к графику функции»
Разделы: Математика
При изучении темы “Касательная к графику функции” можно выделить 5 типов задач.
I. Задачи на составление уравнения касательной к графику функции в точке, принадлежащей графику
Обучение решению задач на касательную осуществляется при помощи алгоритма.
Уравнение касательной к графику функции y=f(x) в точке х



Алгоритм составления уравнения касательной к графику функции y = f(x):
1. Обозначить х 
2. Найти f(х
3. Найти f ‘(x) и f ‘(х



Задача. Составьте уравнение касательной к графику функции


1. х 
3. f ‘(x) = x 2 – 4, f ‘(3) = 5. 4.Подставив в уравнение касательной значения х


Найти уравнение касательной к графику функции f(x) в точке с абсциссой х
1. f(x)=-x -4x+2, х -4x+2, х =-1. =-1. | 1) y=-2x-3; | 2) y=2x-1; | 3) y=-2x+3; | 4) y=2x+3. |
2. f(x)=-x +6x+8, х +6x+8, х =-2. =-2. | 1) y=2x-6; | 2 )y=10x+12; | 3) y=4x+8; | 4) y=-10x+8. |
3. f(x)=x +5x+5, х +5x+5, х =-1. =-1. | 1) y=7x+8; | 2) y=8x+7; | 3) y=9x+8; | 4) y=8x+6. |
4. f(x)=2cosx, х = =  | 1) y= | 2) y= | 3) y= | 4) y= |
5. f(x)=tgx, х = =  1) y=x; 1) y=x; | 2) y=x+ | 3) y=x- | 4) y=x-1. | |
6. f(x)=1-sin2x, х =0. =0. | 1) y=1-2x; | 2) y=2x; | 3) y = -2x; | 4) y=2x+1. |
7. f(x)=  х х =-2. =-2. | 1) y = -x+1; 2) y = x+1; | 3) y = -x-1; | 4) y = -x-2. |
8. Уравнение касательной, проведённой к графику функции y=lnx в точке его пересечения с осью абсцисс, имеет вид. 1) y = 2x-2; 2) y = x-1; 3) y = x+1; 4) y = x.
9. Уравнение касательной, проведённой к графику функции y=e
10. Уравнение касательной, проведённой к графику функции y=sin(x-
Ответы к упражнениям
Задание 1 2 3 4 5 6 7 8 9 10 Номер ответа 3 2 2 2 3 1 3 2 4 4
II. Проведение касательной параллельно заданной прямой
Задача 1. В каких точках касательные к кривой у=

Решение. Так как касательные параллельны прямой у=2х-1 то их угловые коэффициенты совпадают. Т. е. угловой коэффициент касательной в этой точке есть к = 2 .
Находим у’ = х



Решив уравнение х













Ответ: (3;-2) и (-1;
Задача 2. Найти абсциссу точки, в которой касательная к графику функции f(x) = 2x-lnx, параллельна прямой у = х.
Решение. Пусть х



Решив уравнение 2-

Найти абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у(х).
1. f(x)= х+е , у(х)= -х. , у(х)= -х. | 1) — ; 2) 0; 3) ; 2) 0; 3)  ; 4) 1. ; 4) 1. |
2. f(x)=2 +х, у(х)= 2х. +х, у(х)= 2х. | 1) 1; 2) 4; 3) 0; 4)  . . |
3. f(x)=х -5х, у(х)= -х. -5х, у(х)= -х. | 1) -2; 2) 3; 3) -3; 4) 2. |
| 4. f(x)=2lnх-x, у(х)= 0. | 1) -2; 2) 0; 3) 2; 4) 1. |
5. f(x)=-х-е , у(х)= 4-2х. , у(х)= 4-2х. | 1) 3; 2) 2; 3) 0; 4) –2. |
6. Найти сумму абсцисс точек, в которых касательные к графику функции у=х
7. Найти сумму абсцисс точек в которых касательные к кривой у= 
8. К графику функции у = 

9. К графику функции у =- 

10. На графике функции у = х (х-4) 
Ответы к упражнениям
Задание 1 2 3 4 5 6 7 8 9 10 Номер ответа 2 1 4 2 2 1 4 3 2 1
III. Задачи на касательную, связанные с ее угловым коэффициентом
Задача 1. К графику функции f(x) = 3x


f'(x

k= f ‘(x



f ‘(x


Задача 2. Напишите уравнение касательной к графику функции f(x) = 0,5x 2 – 3x + 1, проходящей под углом 45° к прямой y = 0.
Решение. f ‘(x)= x-3. Из условия f ‘(x



1. x
2. f(4) = 8 – 12 + 1 = – 3.
4. y = – 3 + 1(x – 4). y = x – 7 – уравнение касательной
Задача 3. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=x

Решение. k= f'(x

Находим f ‘(x)= 2xlnx+x
При x



Ответ: 
К графику функции f(x) в точке с абсциссой x 
1. f(x)= 2+x-2x , x , x =1. =1. | 1) -1; 2) –7; 3) 3; 4) 0. |
2. f(x)=  , x , x =8. =8. | 1) 1; 2) 32; 3) 8; 4) 16. |
3. f(x)= 5x -3x -3x -7, x -7, x =-1. =-1. | 1) 21; 2) 14; 3) 9; 4) -21. |
4. f(x)= 3x -2lnx, x -2lnx, x =2. =2. | 1) 10; 2) 8; 3) 11; 4) 11,5. |
5. f(x)=  -x+14, x -x+14, x =1. =1. | 1) -51; 2) –65; 3) 63; 4) 77. |
Найти угловой коэффициент касательной проведённой к графику функции f(x) в точке x
6. f(x)=e -x -x , x , x =1. =1. | 1) e-2; 2) –1; 3) e-1; 4) –2. |
7. f(x)=2sinx+2, x =0. =0. | 1) -2; 2) 0; 3) 4; 4) 2. |
8. f(x)=4cosx-1, x = = . . | 1) 4; 2) 2; 3) -2; 4) 1. |
9. f(x)=2 +3, x +3, x =4. =4. | 1) 3,5; 2) 0,5; 3) 7; 4) 2,5. |
10. Под каким углом к оси Ох наклонена касательная к графику функции f(x)=3lnx — x



Ответы к упражнениям
Задание 1 2 3 4 5 6 7 8 9 10 Номер ответа 2 3 1 3 2 1 4 3 2 4
IV. Нахождение касательной проходящей через точку, внешнюю по отношению к заданному графику
Задача 1. Составить уравнения касательных к кривой y = x
При х =2, находим у = 4-8+3=-1

Пусть (х
у ‘ =2х-4, k = 2x
у






Решим уравнение x



x









Таким образом, получили две точки касания А(0;3) и В(4;3). Итак, существуют две касательные к данной кривой; одна из них имеет угловой коэффициент k



Ответ: у =-4х+3, у = 4х-13.
Через точку М(х;у) проведены две касательные к графику функции f(x). Найти сумму абсцисс точек касания.
1. f(x)=4х -8х-2, М(3;-90). -8х-2, М(3;-90). | 1) 4; 2) 6; 3) 5; 4) 3. |
2. f(x)=7х -2х-5, М(2;-93). -2х-5, М(2;-93). | 1) 4; 2) 6; 3) 5; 4) 3. |
3. f(x)=6х -4х-1, М(1;-23). -4х-1, М(1;-23). | 1) 1; 2) 5; 3) 2; 4) 3. |
4. f(x)=х -8х-2, М(1,5;-54). -8х-2, М(1,5;-54). | 1) 2; 2) 4; 3) 5; 4) 3. |
5. f(x)=х -9х-5, М(-1,5;4,5). -9х-5, М(-1,5;4,5). | 1) -2; 2) -5; 3) 2; 4) — 3. |
6. f(x)=7х -7х-1, М(2;-50). -7х-1, М(2;-50). | 1) 4; 2) 6; 3) 5; 4) 3. |
7. Напишите уравнение касательной к графику функции f(x)= х
1) у = 2х+4; 2) у = -2х+4; 3) у = -4х+4; 4) у = 4х-3.
8. Напишите уравнение касательной к графику функции f(x)= х
1) у = 2х+1; 2) у = х+1; 3) у = -х+1; 4) у = -2х-5.
9. Напишите уравнения касательных к графику функции f(x)= -0,5 х
1) у = х+3,5 и у = х-3,5 ; 2) у = -х+3,5 и у = х+3,5; 3) у = -х+4 и у =х+4; 4) у = -х+3 и у =х+3.
10. Через точку В(-2;3) проходят касательные к графику функции у=
1) у = 2х+2 и у = -22х+2; 2) у =-х+3 и у = х-3; 3)у =-0,5х+2 и у =х+4; 4)у =-0,5х+2 и у =-0,1х+2,8.
Ответы к упражнениям
Задание 1 2 3 4 5 6 7 8 9 10 Номер ответа 2 1 3 4 4 1 2 4 2 4
V. Нестандартные задачи, связанные с касательной
1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3. Ответ: y = – 4x + 3, y = 6x – 9,5.
2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x0 = 1, проходит через точку M(2; 3)? Ответ: a = 0,5.
3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2? Ответ: p1 = – 10, p2 = 2.
4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16). Ответ: A(2; – 2), B(– 4; 52).
5. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0. Ответ: M(2; 3).
6. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж. Ответ: y = 2x – 4.
7. На параболе y = x 2 взяты две точки с абсциссами x1 = 1, x2 = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.
Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.
8. Найдите угол 

9. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5. Ответ: y = – 3x и y = x.
10. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.
Ответ: 

11. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N. Ответ: K(1; – 9).
12. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15? Ответ: – 1; 31.
13. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.
14. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x0 = 2, проходит через точку M(1; 8)?
Видео:Уравнение касательной к графику функции | Алгебра 10 класс #45 | ИнфоурокСкачать

Урок алгебры в 10 классе по теме «Уравнение касательной к графику функции»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Выберите документ из архива для просмотра:
Выбранный для просмотра документ конспект урока.docx
Урок изучения нового материала в 10 классе
«Уравнение касательной к графику функции»
УМК: Алгебра и начала математического анализа. 10-11 классы
(базовый уровень) 2011 год
Авторы учебника: А.Г. Мордкович, Л.О. Денищева и др.
Тип урока: изучение нового материала
Тема: Уравнение касательной к графику функции
Цель: вывести формулу уравнения касательной к графику функции в заданной точке, составить алгоритм нахождения уравнения касательной, научиться составлять уравнение касательной.
отработать и систематизировать навыки и умения по теме «Касательная, уравнение касательной к графику функции».
способствовать развитию внимания;
способствовать развитию навыков устного счета;
способствовать развитию логического мышления, математической интуиции;
способствовать развитию и пониманию у учащихся меж предметных связей;
развивать у учащихся коммуникативные компетенции (культуру общения, умение работать в группах, умение аргументировать свою точку зрения);
создавать условия для осознания необходимости самостоятельных действий при решении проблем;
осознавать большую практическую и историческую значимость производной.
Оборудование: компьютер, проектор, презентация, учебник, программа «Живая математика», чертежи графиков функций в программе «Живая математика».
Структура и план урока:
1.Мотивация (самоопределение) к учебной деятельности.
2.Актуализация знаний и фиксация затруднения в деятельности.
3.Постановка учебной задачи.
4.Открытие нового знания.
5.Первичное закрепление во внешней речи.
6.Самостоятельная работа с самопроверкой по эталону.
7.Включение нового знания в систему знаний и повторение.
8.Рефлексия деятельности (итог урока).
1.Мотивация (самоопределение) к учебной деятельности.
Цель: включение учащихся в деятельность на личностно-значимом уровне. (Хочу, потому что могу) (2-3 мин).
Доброе утро! Прошу садиться! Тему урока попрошу определить самостоятельно. Для этого на доске расположены карточки (термины, фамилии и портреты ученых, новые слова и понятия) в хаотичном порядке по теме «Производная функции». К доске выходят 3-4 ученика и располагают их в соответствии с изучением темы (что они уже знают). Домашним заданием было узнать, кто из ученых внес весомый вклад в развитие производной, значение слов «флюксия» и «флюента». Учащиеся с места помогают. После того, когда все приведено в порядок, остается карточка «Уравнение касательной к графику функции». Ученики делают вывод, что это тема сегодняшнего урока. Слайд 1
2.Актуализация знаний и фиксация затруднения в деятельности.
Цель: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося (5-7 мин).
Задача 9 слайда презентации: «Составьте уравнение касательной к графику функции f(x) = x 2 +3x+1в точке с абсциссой х 0 =1» выводит к следующему этапу урока.
3.Постановка учебной задачи.
Цель: обсуждение затруднений. Почему возникли затруднения? Чего мы еще не знаем? (1-2 мин) Учащиеся формулируют цели и задачи урока.
4.Открытие нового знания.
Цель: построение проекта выхода из затруднения (5-7 мин)
В качестве дополнительного домашнего задания 2 «сильным» ученикам Шеину Ивану и Коневу Виталию было предложено разобраться с помощью учебника с выводом общей формулы уравнения касательной (учебник страница 174) и примером на составление уравнения касательной к графику функции 2 в точке х= 1 (учебник страница 166, пример 2).
Учащиеся записывают свои выводы на доске, остальные записывают в тетрадь. После вывода учащихся учителем демонстрируется чертеж 1, выполненный в программе «Живая математика» (график функции и касательная к нему в точке) и слайд 10 с уравнением касательной.

5.Первичное закрепление во внешней речи.
Цель: проговаривание нового знания, запись в виде опорного сигнала (5 мин).
Класс делится на 4 группы, которым предлагается создать алгоритм составления уравнения касательной к графику функции. Учащиеся пользуются только общим уравнением касательной. После обсуждения проговаривают алгоритм по пунктам, дополняют, исправляют. В результате демонстрируется слайд 11.
6.Самостоятельная работа с самопроверкой по эталону.
Цель: каждый для себя должен сделать вывод о том, что он уже умеет (5-6 мин).
На этом этапе возвращаемся к задаче слайда 9 о составлении уравнения касательной, учащиеся решают самостоятельно с последующей самопроверкой. Слайд 12, а также чертеж 2 «Живой математики».


7.Включение нового знания в систему знаний и повторение.
Цель: выполняются упражнения, в которых новое знание используется вместе с изученным ранее (10-12 мин).
Работа с задачником: страница 91, самостоятельный выбор номера из №№ 29.12 – 29.16 (ответы есть в учебнике). Ученики имеют возможность выбрать задания по уровню сложности.
ДОМАШНИМ ЗАДАНИЕМ будут эти же номера 29.12 – 29.16, отработать составление уравнения касательной, используя алгоритм. Решить не менее 3 букв, не считая выполненных в классе.
8.Рефлексия деятельности (итог урока).
Цель: осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и всего класса (2-3 мин).
-Какую задачу ставили?
-Удалось ли решить поставленную задачу?
-Какие получили результаты?
-Где можно применить новые знания?
И, наконец, после «всяких умных вещей» немного юмора. На экране представлены графики зависимости уровня ваших знаний от времени, в интервале от начала урока до его завершения.

Пожалуйста, выберите тот график, который, на ваш взгляд, наиболее вам близок. Имеют ли они отношение к теме нашего урока? По этим графикам можно судить о скорости приращения ваших знаний в ходе урока. График 1 – мы достигли цели и решили задачи, поставленные в начале урока.
Спасибо за урок!
Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч.1,2. Учебник и задачник для учащихся общеобразовательных учреждений (базовый уровень)/ под ред. А. Г. Мордковича. — М.: Мнемозина, 2011.
Живая математика: сборник методических материалов. – М.: ИНТ. 176 с.
В. М. Чернявский Работа с программой «Живая математика».
Различные Интернет-ресурсы для поиска детьми дополнительной информации по теме «Производная».
Выбранный для просмотра документ урок 10 уравнение касательной.ppt
🎬 Видео
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Касательная к графику функции в точке. 10 класс.Скачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Уравнение касательной к графику функции в задачах. Часть 1. Алгебра 10 классСкачать

Уравнение касательной к графику функции в задачах. Часть 4. Алгебра 10 классСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Уравнение касательной к графику функции. Алгебра 10 классСкачать

Уравнение касательнойСкачать

Как составить уравнение касательной и нормали к графику функцииСкачать

Уравнение касательной к графику функции в задачах. Часть 5. Алгебра 10 классСкачать

Производная: касательная к графику.Скачать

Алгебра и начала анализа 10 класс Уравнение касательной к графику функции 03 02 2021Скачать

10 класс. Уравнение касательнойСкачать

Уравнение касательнойСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Уравнение касательной к графику функции в заданной точкеСкачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.Скачать