Проверка обоснованности включения и исключения группы новых переменных в уравнение регрессии

Регрессионный анализ — это не только выбор аппроксимирующей функции и расчет ее коэффициентов на основе метода наименьших квадратов. Построенная модель должна быть обоснованной с точки зрения ее соответствия исследуемому объекту (процессу, явлению и т.д.) и эмпирическим данным. Проверка обоснованности модели включает в себя три момента |6|:

• 1) качественный анализ возможного вида функции с точки зрения содержания и законов развития объекта исследования (если, например, динамика роста цен на определенный товар не предполагает резкого изменения, то для прогнозирования этого процесса не следует использовать квадратическую или кубическую регрессионную модель);
• 2) проверка адекватности модели, т.е. ее соответствия имеющимся эмпирическим данным;
• 3) оценка статистической значимости (надежности) модели в целом и ее параметров, т.е. оценка их неслучайности: насколько параметры модели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств.

При этом, разумеется, предполагается, что все предпосылки применения регрессионного анализа, рассмотренные в предыдущем параграфе, выполняются, т.е. проведена проверка их выполнения.

Первый этан проверки обоснованности модели предполагает привлечение знаний из конкретных экономических, социологических и других дисциплин (например, микро- или макроэкономики). На этом этапе делается заключение о том, насколько вид используемой функциональной зависимости и характер влияния факторных признаков на результативный могут соответствовать исследуемому процессу. О характере влияния факторных признаков на результативный признак в первую очередь свидетельствуют знак и величина соответствующего коэффициента регрессии, а также степень соответствующей независимой переменной. Например, если коэффициент перед независимой переменной имеет положительное значение, то с увеличением данного фактора результативный признак возрастает. Но интерпретация этих величин должна соответствовать социально-экономическому содержанию моделируемого признака. Если теория указывает, что факторный признак должен иметь положительное значение, а в уравнение регрессии он входит с отрицательным знаком, то необходимо проверить расчеты параметров уравнения регрессии и (или) выбрать другую регрессионную модель.

Адекватность и значимость модели проверяются с помощью математико-статистических подходов, методов и показателей, которые и являются главным предметом рассмотрения данного и следующих параграфов этой главы.

Адекватность регрессионных моделей — это их соответствие фактическим статистическим данным. Регрессионная модель считается адекватной, если теоретические значения зависимой переменной (т.е. предсказанные на основе модели) согласуются с результатами наблюдений.

Исходное предположение для проверки адекватности регрессионной модели заключается в том, что зависимость между прогнозируемым (теоретическим) значением результативного признака (у) и факторами (x_t) имеет вид

где с — некоторая случайная величина, связанная с влиянием неконтролируемых или неучтенных факторов, случайных ошибок измерения или с тем, что самой природе объекта исследования свойственны случайные процессы. Именно из-за г возникают ненулевые остатки, т.е. разности между теоретическими и эмпирическими значениями (y_i -#,). Предполагается также, что эти остатки независимы (некоррелированы) и распределены но нормальному закону с нулевым средним и одинаковой дисперсией. Это предположение легко проверить путем построения диаграммы остатков.

Поэтому общий подход к проверке адекватности полученной модели заключается в нахождении остатков, а точнее — значения суммы квадратов разностей между наблюдаемыми и предсказанными моделью значениями переменной у. Этот показатель обычно обозначается как SS_e (от sum of squares). Далее вычисляются статистические показатели, на основе которых можно судить об адекватности полученной модели (основным здесь является F-критерий — критерий Фишера).

Для адекватной модели, кроме некоррелированности остатков и их нормального распределения, должно выполняться условие гомоскедастичнос— ти, т. е. постоянства дисперсии ошибок для всех наблюдений. Оценка выполнимости этого условия проводится по графику остатков: если все остатки укладываются в симметричную относительно нулевой линии полосу, то можно считать, что дисперсия ошибок наблюдений постоянна. На графике распределения значений зависимой переменной от одной из независимых переменных не должно быть сильных «раздуваний». Значительное отклонение от этого условия называется гетероскедастичностъю. Для оценки гетероскедастичности разработаны и специальные статистические тесты.

Таким образом, основным показателем отклонений данных от модели может служить сумма квадратов разностей теоретических и эмпирических значений зависимой переменной у. Чем этот показатель меньше, тем приближение лучше, следовательно, построенная модель лучше описывает реальные данные. На этой основе вычисляется такой показатель адекватности регрессионной модели, как остаточная дисперсия:

Но при этом следует учитывать, что если в модель добавляется новый параметр, то сумма квадратов, как правило, оказывается меньше (т.е. многочлен второй степени лучше соответствует данным, чем линейная функция, многочлен третьей степени лучше приближает исходные данные, чем многочлен второй степени, и т.д.). В конце концов можно дойти до многочлена степени (п- 1) с п коэффициентами, который проходит через все заданные точки, т.е. разница между эмпирическими и теоретическими значениями у будет равна нулю [16]. Но прогностические возможности такой модели существенно меньше, чем у линейной функции. Излишнее усложнение статистических моделей вредно. Даже если адекватность простых функций незначительно меньше, чем более сложных, рекомендуется выбирать более простую функцию.

Поэтому показатель адекватности регрессионной модели, использующий оценку остаточной дисперсии, корректируется на число параметров модели (т):

В случае парной регрессии скорректированная оценка остаточной дисперсии имеет вид

поскольку число оцениваемых параметров т = 2.

Корень квадратный из этого показателя называется стандартной ошибкой оценки (standard error of estimate) и на практике используется для характеристики точности, с которой можно оценивать и прогнозировать значение результативного признака. При этом данный показатель интерпретируется аналогично стандартной ошибке среднего при построении доверительных интервалов (см. параграф 7.3). Например, среднее предсказанное значение зависимой переменной при определенном значении независимой переменной (или переменных в случае множественной регрессии) с вероятностью 0,95 будет лежать в пределах приблизительно двух величин стандартной ошибки оценки по обе стороны от значения у_у предсказанного на основе регрессионной модели:у ± 1,96а 2 .

Отметим, что сравнение адекватности моделей разных видов (например, линейных и нелинейных) по величине стандартной ошибки оценки может оказаться некорректным, если результативный признак в разных моделях может иметь разный масштаб и разные единицы измерения (например, [руб.] И [ 1п(ру6.)]).

Другими важными показателями адекватности регрессионной модели являются коэффициент множественной корреляции (R) и коэффициент множественной детерминации, равный квадрату коэффициента множественной корреляции (R 2 ).

Расчет этих коэффициентов базируется на следующих рассуждениях. Чем меньше остаточная дисперсия а 2 по отношению к общей дисперсии а 2

результативного признака (с*= —-), тем лучший прогноз можно

Например, если связь между переменными х и у полностью отсутствует, то отношение остаточной дисперсии переменной у к исходной дисперсии результативного признака равно единице. Если модель полностью адекватна, то остаточная дисперсия отсутствует, и отношение дисперсий будет равно нулю. В большинстве случаев это отношение будет лежать в диапазоне от 0 до 1. Коэффициент множественной детерминации определяется как

где SS = X _ У) 2

сумма квадратов отклонений зависимой переменной

Иначе R 1 можно определить как

УУ — сумма квадратов отклонений прогнозных (теорети-

ческих) значений зависимой переменной от среднего (сумма квадратов, обусловленная регрессией); SS_y = SS_R + SS_e.

Если, например, R 2 = 0,6, то 60% изменчивости результативного признака может быть объяснено (предсказано) на основе регрессионной модели, а 40% остаточной дисперсии остаются необъясиенными (неучтенными). Таким образом, значение R 2 является индикатором степени адекватности регрессионной модели (значение R 2 , близкое к единице, показывает, что модель объясняет почти всю изменчивость результативного признака). Иногда R 2 называют показателем прогностической силы регрессионной модели.

В случае множественной регрессионной модели коэффициент множественной детерминации R 2 всегда больше коэффициентов парной детерминации г 2 , полученных для результативного признака и каждой из независимых переменных на основе связи такого же вида, что и в построенной модели. Но обычно коэффициент множественной детерминации меньше, чем сумма соответствующих парных коэффициентов. Однако иногда возможны ситуации синергетического эффекта, когда комбинация нескольких переменных в регрессионной модели объясняет изменчивость результативной переменной лучше, чем простое суммирование эффектов влияния на результативный признак каждой из независимых переменных по отдельности.

При включении дополнительных независимых переменных в регрессионную модель К 1 всегда возрастает, даже если включаемая переменная не имеет смысловой связи или даже значимой корреляционной связи. Подобное «техническое» увеличение показателя R 2 может искажать представление об адекватности конструируемой регрессионной модели, поэтому на практике используют также скорректированный К 1 (adjusted R 2 ), учитывающий возможное «техническое» влияние дополнительных переменных на изменчивость результативного признака:

где п — число наблюдений; т — число параметров модели.

Если при включении дополнительной переменной в регрессионную модель значение этого показателя уменьшается или остается примерно тем же, это в большинстве случаев означает, что данная переменная реально не объясняет изменчивость результативного признака, поэтому ее не следует включать в регрессионное уравнение.

При конструировании регрессионной модели следует исходить из принципа парсимонии (parsimony): нужно объяснять изменчивость результативного признака с помощью минимального числа независимых переменных (г.е. чем проще модель, обеспечивающая приемлемую адекватность, гем она лучше). Более простой модели проще придать разумную интерпретацию, т.е. объяснить изменение результативного признака с точки зрения содержательно-смысловых, а не абстрактно-математических связей.

Коэффициент множественной корреляции по определению равен корню квадратному из коэффициента детерминации. Это неотрицательная величина, принимающая значения между 0 и 1. Коэффициент множественной корреляции — это мера линейной связи зависимой переменной с множеством независимых переменных, включенных в модель. На практике коэффициент множественной корреляции можно определить как коэффициент парной корреляции между теоретическими и эмпирическими значениями результативного признака. Для парной регрессии R равен коэффициенту корреляции между у и х.

Более тщательная проверка адекватности регрессионной модели может быть проведена, если для зависимой переменной осуществлены повторные наблюдения. В этом случае для проверки адекватности модели используется следующая процедура. Если модель адекватна, то эмпирические значения у должны быть близки значениям, предсказанным регрессионной моделью. Мерой неадекватности модели будет сумма квадратов отклонений этих значений. Чем меньше она будет, тем лучше результаты наблюдений согласуются с моделью.

Иногда для оценки адекватности регрессионную модель строят не но всему имеющемуся набору данных, а по меньшему числу наблюдений. Оставшиеся наблюдения используются для проверки адекватности, как и в случае повторных измерений. Если при этом модель признается достаточно адекватной, то для уточнения параметров модели вновь строится уравнение регрессии на основе выбранного вида аппроксимирующей функции.

Регрессионный анализ, как и корреляционный, обычно проводится по выборке из генеральной совокупности. Поэтому показатели регрессии и корреляции — параметры уравнения регрессии, коэффициенты множественной корреляции и детерминации — могут быть искажены действием случайных факторов. Чтобы проверить, насколько эти показатели характерны для всей генеральной совокупности, необходимо проверить их статистическую значимость (иногда говорят «существенность» или «достоверность»). При этом выясняют, насколько каждый из вычисленных параметров регрессии (включая коэффициент а₀ — постоянный член регрессии) характерен для генеральной совокупности, т.е. не является ли полученное значение результатом действия случайных причин или стечения случайных обстоятельств.

Логика проверки коэффициентов множественной корреляции и детерминации, а также параметров регрессии в целом аналогична логике проверки статистических гипотез (см. параграф 7.4). Например, значимость коэффициентов парной линейной регрессии проверяют с помощью ^-критерия Стьюдента. Эмпирические значения ^-критерия для параметра а₀ вычисляются по формуле

а для параметра я, — по формуле

гдеду — среднее квадратичное отклонение эмпирических значений результативного признака у от теоретических значений г/ (корень квадратный из остаточной дисперсии):

о_г — среднее квадратичное отклонение факторного признака х от его среднего значения х (корень квадратный из дисперсии х):

п — объем выборки.

Эмпирические значения t, вычисленные по вышеприведенным формулам, сравнивают с критическими значениями t, которые определяют из соответствующей статистической таблицы ^-распределения Стьюдента (см. приложение П4) с учетом принятого уровня значимости а и числом степеней свободы df =п — 2. Параметр регрессионной модели признается значимым при условии, если г_{эмпиричсскос} > ^критическое* в этом случае маловероятно, что найденные значения параметров обусловлены только случайными совпадениями.

В общем случае при проверке статистической значимости коэффициентов регрессии р,, i = 0,1. п> нулевая гипотеза формулируется как Н₀: р,= О, а альтернативная — Н_А: р, Ф 0 (г.е. проверяется ненаправленная альтернативная гипотеза). Если нулевая гипотеза отклоняется, соответствующая переменная может быть включена в регрессионное уравнение, иначе переменную не следует включать. На практике статистическая значимость параметров модели оценивается с помощью статистических пакетов, определяющих /^-уровень значимости, на основе которого принимают решение об отклонении или невозможности отклонения нулевой гипотезы. Еще раз отметим, что статистическая значимость параметров — не единственный критерий принятия окончательного решения о включении переменной в модель. Другими критериями являются экономический смысл переменных и их возможных связей, изменение R 2 и скорректированного /? 2 , наличие и степень мультиколлинеарности и др.

В случае множественной регрессии с большим числом факторов необходимо классифицировать эти переменные по степени их важности для предсказания зависимой переменной (у). Затем следует исключить из анализа факторы, наименее существенные для предсказания у, а также переменные, сильно коррелированные с другими, уже включенными в модель факторами. Эту задачу можно определить как выбор наилучшей регрессии, т.е. определение минимального набора факторов, достаточно точно предсказывающих значение результативного признака.

Одним из методов отбора наиболее существенных факторов является пошаговая регрессия (stepwise regression). Рассмотрим две процедуры пошаговой регрессии: обратную (backward) и прямую <forward).

Обратная пошаговая регрессия заключается в том, что последовательно исключаются наименее значимые факторы. На нулевом шаге проводится регрессионный анализ для всех факторов. Каждый фактор проверяется на значимость. Если показатель статистической значимости меньше критического значения, то фактор исключается из анализа и строится новое уравнение регрессии по оставшимся факторам (критический p-уровень значимости задается на уровне 0,1 или 0,05).

Прямая пошаговая регрессия организована в противоположном направлении: на первом шаге в уравнение регрессии включается фактор, имеющий наибольший коэффициент корреляции с у, и проверяются адекватность и значимость модели. Если модель значима, включается следующий фактор и вычисляется статистика значимости для каждой переменной модели. Если статистический показатель значимости какой-либо переменной меньше заданной критической величины, то фактор исключается, если больше — сохраняется, и в уравнение включается следующая переменная. Поскольку проверка всех выбранных переменных осуществляется на каждом шаге, может оказаться, что переменная, включенная в уравнение на предыдущем шаге, может быть исключена на следующих шагах.

Рассматривая причины исключения переменных, мы обращали внимание лишь на статистические показатели. В реальном исследовании необходимо обращаться и к смысловому содержанию переменных. Исследователь может принять решение остановиться не на последнем шаге конструирования модели, а на одном из предыдущих шагов, если, по его мнению, некоторые переменные очень важны для объяснения и прогнозирования результативного признака. Но в этом случае, возможно, понадобятся дополнительные данные (наблюдения, измерения и т.п.) для достижения приемлемой статистической значимости моделей и ее параметров. Необходимо помнить также, что для принятия окончательных выводов но результатам регрессионного анализа должны дополнительно проверяться предпосылки его применения.

Теоретически процедуры прямой и обратной пошаговой регрессии должны приводить к одной и той же регрессионной модели при условии независимости всех рассматриваемых переменных. В случае если какие-либо переменные (например, x_i и х_>) сильно коррелируют, возможна ситуация, когда процедура прямой пошаговой регрессии приведет к включению в модель переменной x_jy а обратной — х-. Болес часто на практике используют процедуру обратной пошаговой регрессии.

В заключение этого параграфа обратим внимание читателя на соотношение числа наблюдений и количества параметров регрессионной модели. Этот вопрос особенно важен, когда число наблюдений относительно мало по сравнению с числом независимых переменных. Например, понятно, что «неразумно» делать выводы из анализа анкеты с 50 пунктами на основе ответов 10 респондентов. Минимально необходимое число наблюдений для построения регрессионной модели (п) должно быть не меньше числа всех признаков, включенных в модель (т), в том числе результативного. Но рекомендуется использовать не менее 10 наблюдений на одну независимую переменную [6].

Видео:Множественная регрессия в ExcelСкачать

Методы отбора переменных в регрессионные модели

Видео:Множественная регрессияСкачать

Введение

При всем существующем разнообразии методов Data Mining, практически все они сталкиваются с общей трудностью – вопросом отбора значимых для модели входных признаков (в зарубежной литературе такая проблема известна как feature selection).Сокращение числа независимых переменных призвано уменьшить размерность модели не только с тем, чтобы удалить из нее все незначащие признаки, не несущие в себе какой-то полезной для анализа информации, и тем самым упростить модель, но и чтобы устранить избыточные признаки. Дублирование информации в составе избыточного признака не просто не улучшает качество модели, но и порой, наоборот, ухудшает его (как, например, в случае с мультиколлинеарностью).

Очевидно, что одним из возможных выходов из сложившейся проблемы могло бы стать построение модели на всех возможных комбинациях наборов входных признаков с последующим отбором того варианта, который обладал бы наилучшей описательной способностью результирующего признака $Y$ и при этом содержал бы минимум независимых переменных. Однако такое решение возможно лишь при наличии незначительного количества факторов-претендентов на включение в модель. В случае же относительно большого списка потенциальных признаков подобная методика представляется достаточно затруднительной, так как количество моделей, которые необходимо будет построить, оказывается крайне велико и в общем случае равно $2^n$ – 1 штука (так называемое «проклятие» размерности). Ввиду этого необходимо иметь на вооружение какие-то иные алгоритмы отбора наиболее важных факторов, которые потребовали бы значительно меньших затрат усилий, а соответственно и времени.

Существует различные методики решения данной проблемы. В случае с регрессионной моделью достаточно хорошо себя зарекомендовали такие методы, как:

• процедура Forward Selection (прямой отбор),
• процедура Backward Elimination (обратное исключение),
• процедура Stepwise,
• процедура Best Subsets (лучшие подмножества).

Рассмотрим работу данных методов на примере множественной регрессии.

Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Частный F-тест

Перед тем, как начать знакомиться непосредственно с самими методами отбора переменных в регрессионные модели, рассмотрим сущность критерия, называемого частным F-тестом, на основе которого, собственно, и разработаны первые 3 методики.

Критерий призван оценить целесообразность ввода дополнительной независимой переменной в линейную модель множественной регрессии, уравнение которой, как известно, имеет вид:

$Y= beta_0+ beta_1 X^ + dots + beta_n X^ + varepsilon$, (1)

$beta_0,,beta_1,,dots,,beta_n$ – параметры модели,

$varepsilon$ – случайная составляющая.

Идея этого критерия основана в первую очередь на таком базовом понятии, как сумма квадратов регрессии $SSR$:

$widehat$ – оценка, полученная на основе регрессионной модели,

$overline$ – среднее по всем наблюдениям $Y$,

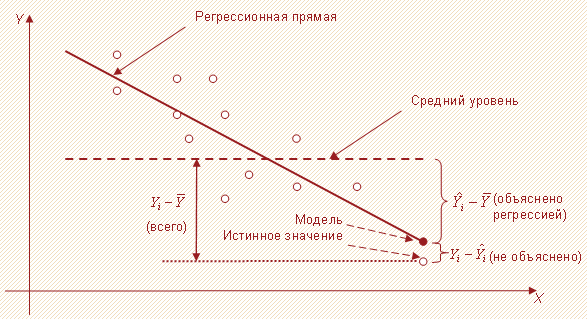
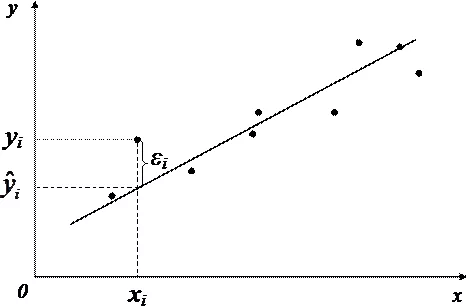
Данный показатель характеризует ту долю общей вариации (изменчивости) результативного признака $Y$, которую получилось объяснить при помощи регрессии. Проиллюстрируем данный факт на примере простейшей однофаторной линейной модели (рисунок 1).

Поясним рисунок 1. Очевидно, что если бы регрессия не включала бы ни одного фактора, то модель бы выдавала значения, равные $overline$. Соответственно, разности $Y_i,-,overline,(i = 1,,2,,dots,,n)$ представляли бы собой необъясненные случайные отклонения. Благодаря же вводу независимой переменной $X$ оценки, полученные на основании модели, стремятся оказаться как можно ближе к реальным значениям случайной величины $Y$. В связи с этим каждое расстояние $Y_i,-,overline$ может быть разложено на 2 составляющие:

$widehat,-,overline $ – было объяснено регрессией,

$Y_i,-,widehat $ – не удалось объяснить.

Соответственно, модель оказывается тем лучше, чем ближе к нулю величины $Y_i,-,widehat,,i = 1,,2,,dots,,n$.

Теперь предположим, что на основе переменных $X^,X^,dots,X^ $ была построена регрессионная модель, для которой доля изменчивости, объясненная линейной зависимостью, составила величину $SSR^$. Допустим, что мы хотим ввести в модель новый признак $X^$.

Сумма квадратов регрессии $SSR$, построенной на независимых переменных $X^,,X^,,dots,X^$ и $X^$, составляет $SSR$.

Очевидно, что $SSR^geq SSR^$.

Рассчитаем, насколько увеличилась объясняющая способность модели в результате ввода новой переменной $X^$:

Таким образом, $SSR^$ можно назвать вкладом переменной $SSR^$ в объяснение общей изменчивости результативного признака $Y$. Очевидно, чем больше данное значение, тем весомей этот вклад. Тогда возникает вопрос:

«Каким образом следует выбрать порог для $SSR^$, чтобы признать эту величину достаточно большой и, соответственно, принять решение о значимости признака $^$?».

С ответом на этот вопрос может помочь так называемый частный F-тест. По сути, данный критерий призван проверить следующую гипотезу:

H₀: вклад $SSR$, вносимый $X^$, не достаточно велик, ввиду чего эту переменную не следует включать в модель

H₀: вклад $SSR^$, вносимый $X^$, значительный, и потому эту переменную следует включить в модель

Для того чтобы проверить эти гипотезы, следует перейти от рассматриваемого показателя $SSR^$ к статистике следующего вида:

где $MSE^$ представляет собой сумму квадратов ошибок $SSE$ (модель построена по переменным $X^,,X^,,dots,X^$ и $X^$), приходящуюся на одну степень свободы $df^$.

Значение $MSE^$ может быть найдено по формуле:

$Y_i$ – истинное значение результирующей переменной,
$widehat$ – оценка, полученная на основании регрессионной модели,
$n$ – объем выборки,
$k$ – количество переменных исходной модели (без $X^$).

Доказано, что статистика, сформированная в соответствии с (4), при справедливости гипотезы H₀ распределена по закону Фишера (F-распределение).
Тогда проверка гипотезы H₀ будет сводиться к следующей последовательности действий:

1. Задаемся уровнем значимости $alpha$, например 0,01 или 0,05.
   Данная величина характеризует риск принятия неправильного решения.
2. По специальным таблицам находим $00,alpha$-процентную точку $K_$ распределения Фишера со степенями свободы $d1= 1$ и $d2 = n-k-2$. Это значение будет являться граничным для статистики $ gamma$ (4).
3. Сравниваем найденную $100,alpha$-процентную точку $K_$ со значением статистики $gamma$.
   Если окажется, что $gamma,>,K_$, то делается вывод о значимости признака $X^$ и, соответственно, его следует включить в модель (отдается предпочтение гипотезе H₁ с вероятностью $alpha$ ошибиться).
   Если же $gamma,leq ,K_ $, то принимается решение о неэффективности включения переменной $X^$ в модель (то есть гипотеза H₀ принимается с вероятностью $1,-,alpha$ как не противоречащая экспериментальным данным).

Замечание. Вопрос проверки гипотез H₀ и H₁ на основе F-критерия можно рассмотреть несколько в ином русле, а именно, не задаваясь уровнем значимости $alpha$, найти вероятность того, что случайная величина $gamma$ примет значение большее, чем рассчитанный критерий. Так как закон распределения данной статистики нам известен, то сделать это совсем не сложно. Соответствующую величину можно найти следующим образом:

$alpha_ = 1,-,pFbigl(gamma,,d_1,, d_2bigr)$,

$pFbigl(gamma,,d_1,, d_2bigr)$ – значение функции распределения Фишера в точке $gamma$;
$d_1,, d_2$ – количество степеней свободы.

Теперь, если найденная величина $alpha_$ окажется достаточно маленькой, то следует принять решение о включении переменной $X^$ в модель. В противном случае эту идею нужно отвергнуть.

Теперь, когда мы рассмотрели методику принятия решения о включении отдельной независимой переменной в модель (или, наоборот, нецелесообразности этого поступка), можем перейти к освещению идей, заложенных в основу алгоритмов отбора значимых факторов.

Видео:Парная регрессия: линейная зависимостьСкачать

Методы отбора переменных

Видео:Регрессия в ExcelСкачать

Метод прямого отбора (Forward Selection)

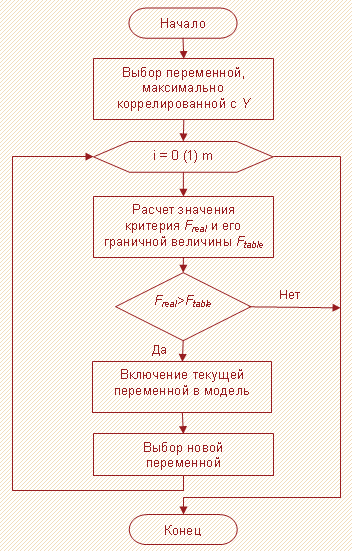
Данный алгоритм включает в себя следующие шаги:

1. Из списка всех возможных входных переменных выбирается та, которая имеет наибольшую корреляцию с $Y$, после чего модель, содержащая лишь одну выбранную независимую переменную, проверяется на значимость при помощи частного F-критерия. Если значимость модели не подтверждается, то алгоритм на этом заканчивается за неимением существенных входных переменных. В противном случае эта переменная вводится в модель и осуществляется переход к следующему пункту алгоритма.
   Следует отметить, что в данном случае проверка на значимость всей модели в целом будет равносильна проверке на значимость выбранной независимой переменной, так как на данном этапе модель еще не содержит других входных переменных.
2. По всем оставшимся переменным на основании формулы (4) рассчитывается значение статистики $ gamma$, которая представляет собой отношение прироста суммы квадратов регрессии, достигаемая за счет ввода в модель соответствующей дополнительной переменной (по сравнению с величиной $SSR^$, рассчитанной только лишь на основе ранее уже введенных переменных), к величине $MSE^ $.
3. Из всех переменных-претендентов на включение в модель выбирается та, которая имеет наибольшее значение критерия, рассчитанного в пункте 2.
4. Проводится проверка на значимость выбранной в пункте 3 независимой переменной. Если ее значимость подтверждается, то она включается в модель, и осуществляется переход к пункту 2 (но уже с новой независимой переменной в составе модели). В противном случае алгоритм останавливается.

Процедуру отбора независимых переменных по методу Forward Selection можно представить в виде блок-схемы, изображенной на рисунке 2.

Видео:Коэффициент линейной регрессии, 2 способаСкачать

Метод обратного исключения (Backward Elimination)

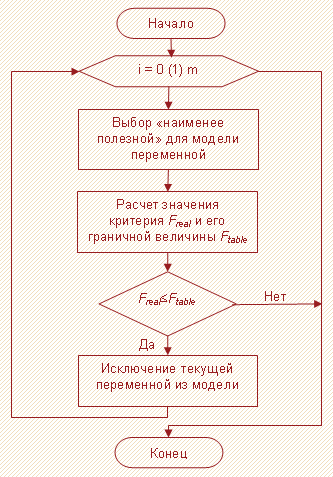
Данная процедура похожа на предыдущий метод, но с тем отличием, что теперь уже изначально включены в модель все переменные и постепенно осуществляется «отсеивание» тех из них, которые не проходят проверку на значимость.

1. В модель включаются все имеющиеся независимые переменные.
2. По переменным, включенным к данному моменту в модель, рассчитывается величина, представляющая собой разность между суммой квадратов регрессии, построенной по всем текущим переменным модели, и аналогичным показателем, рассчитанным теперь уже без учета одной переменной, для которой вычисляется данный показатель. По каждой найденной величине $SSR_<I^>$ рассчитывается статистика $gamma$.
3. Выбирается переменная с минимальным значением $gamma$.
4. Решается вопрос о целесообразности присутствия в модели выбранной в пункте 3 переменной. Если она не проходит проверку на значимость, то производится ее исключение из модели, после чего осуществляется переход к пункту 2 алгоритма, но уже из расчета, что указанная переменная в модели не присутствует. В противном случае, когда переменная оказывается значимой, алгоритм останавливается.

На рисунке 3 приведена блок-схема процедуры отбора факторов методом обратного исключения.

Видео:Построение модели множественной регрессии в программе GretlСкачать

Метод последовательного отбора (Stepwise)

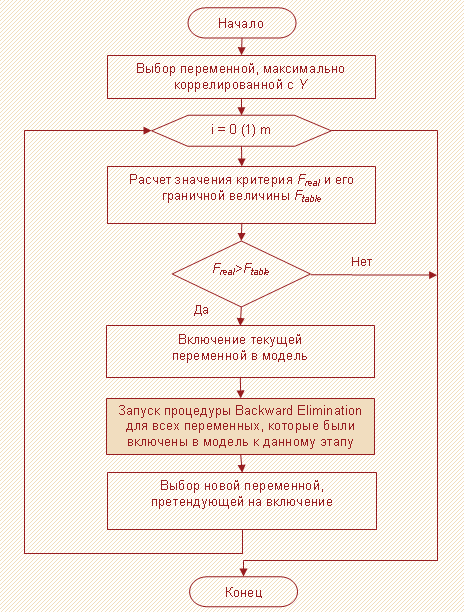
Метод последовательного отбора представляет собой всего лишь модификацию метода прямого отбора, отличающегося от него тем, что на каждом шаге после включения новой переменной в модель осуществляется проверка на значимость остальных переменных, которые уже были введены в нее ранее. В случае, если такие переменные будут обнаружены, то их следует вывести из состава модели. После корректировки списка включенных в модель переменных осуществляется очередная итерация процедуры прямого отбора по поиску новой переменной, удовлетворяющей условиям включения ее в состав модели.

Ниже на рисунке 4 приведена блок-схема соответствующего метода.

Видео:Эконометрика. Линейная парная регрессияСкачать

Отбор на основе «лучших подмножеств» (Best Subsets)

Данный метод предусматривает, что аналитик изначально должен определиться с максимально возможным количеством $p$ входных признаков, задействованных в модели. Далее поступают следующим образом: по всему перечню переменных строятся $p$ групп моделей, причем первую такую группу составляют все однофакторные модели, которые только можно построить на имеющемся наборе признаков, соответственно, во вторую попадают все двухфакторные модели и т. д. вплоть до $p$-й группы (куда входят все модели, включающие $p$ факторов). По всем полученным моделям рассчитываются статистические показатели, характеризующие качество модели, такие как коэффициент детерминации $R^2$, скорректированный коэффициент детерминации $R^2_$, стандартная ошибка оценивания $s$ (равная квадратному корню из суммы квадратов ошибки модели, приходящейся на одну степень свободы $MSE$) и другие. Затем из каждой полученной группы отбираются только $k$ самых лучших моделей с точки зрения рассчитанных показателей, после чего формируется отчет, включающий $k,times,p$ моделей, на основании которого аналитик непосредственно делает окончательное заключение.

Видео:Уравнение регрессииСкачать

Пример использования алгоритмов отбора

Разберем механизм работы описанных выше методов отбора переменных в линейную модель множественной регрессии на конкретном примере. В качестве исследуемых признаков возьмем показатели из банковской сферы, приведенные в таблице 1.

Таблица 1 – Переменные, используемые при построении регрессионной модели

Признак	Обозначение	Тип
Количество просрочек
Стаж на последнем месте работы
Срок кредита	В таблице 2 содержится информация о 10 заемщиках по каждой из заявленных переменных. Видео:Математика #1 | Корреляция и регрессияСкачать R — значит регрессия Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума. Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей. Видео:Парная и множественная линейная регрессияСкачать 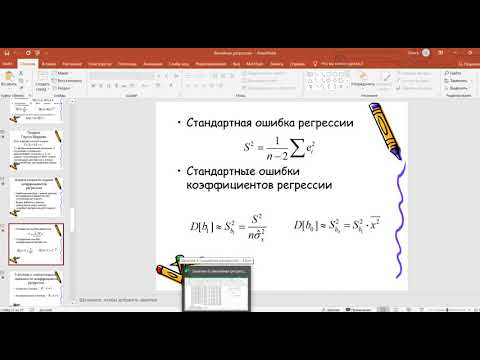Введение в регрессионный анализ Если имеется корреляционная зависимость между переменными y и x , возникает необходимость определить функциональную связь между двумя величинами. Зависимость среднего значения называется регрессией y по x . Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна. Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г. Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия. k — число коэффициентов в системе уравнений регрессии. Чаще всего используется модель линейной регрессии, а все нелинейные зависимости приводят к линейному виду с помощью алгебраических ухищрений, различных преобразования переменных y и x . Линейная регрессия Уравнения линейной регрессии можно записать в виде В матричном виде это выгладит y — зависимая переменная; x — независимая переменная; β — коэффициенты, которые необходимо найти с помощью МНК; ε — погрешность, необъяснимая ошибка и отклонение от линейной зависимости; Случайная величина может быть интерпретирована как сумма из двух слагаемых: — полная дисперсия (TSS). — объясненная часть дисперсии (ESS). — остаточная часть дисперсии (RSS). Еще одно ключевое понятие — коэффициент корреляции R 2 . Видео:Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать Ограничения линейной регрессии Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных. Линейность, собственно. Увеличение, или уменьшение вектора независимых переменных в k раз, приводит к изменению зависимой переменной также в k раз. Матрица коэффициентов обладает полным рангом, то есть векторы независимых переменных линейно независимы. Экзогенность независимых переменных — . Это требование означает, что математическое ожидание погрешности никоим образом нельзя объяснить с помощью независимых переменных. Однородность дисперсии и отсутствие автокорреляции. Каждая εi обладает одинаковой и конечной дисперсией σ 2 и не коррелирует с другой εi. Это ощутимо ограничивает применимость модели линейной регрессии, необходимо удостовериться в том, что условия соблюдены, иначе обнаруженная взаимосвязь переменных будет неверно интерпретирована. Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике. Неоднородность дисперсии При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки. Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно. Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены. Автокорреляция проверяется статистикой Дарбина-Уотсона (0 ≤ d ≤ 4). Если автокорреляции нет, то значения критерия d≈2, при позитивной автокорреляции d≈0, при отрицательной — d≈4. Неоднородность дисперсии — Тест Уайта, , при chi_$» data-tex=»inline»/> нулевая гипотеза отвергается и констатируется наличие неоднородной дисперсии. Используя ту же можно еще применить тест Бройша-Пагана. Мультиколлинеарность — нарушения условия об отсутствии взаимной линейной зависимости между независимыми переменными. Для проверки часто используют VIF-ы (Variance Inflation Factor). В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности. Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений. Видео:Тема по SPSS: способы включения переменных в модель множественной линейной регрессии.Скачать Как преодолеть эти ограничения Нарушения одной или нескольких ограничений еще не приговор. Нелинейность регрессии может быть преодолена преобразованием переменных, например через функцию натурального логарифма ln . Таким же способом возможно решить проблему неоднородной дисперсии, с помощью ln , или sqrt преобразований зависимой переменной, либо же используя взвешенный МНК. Для устранения проблемы мультиколлинеарности применяется метод исключения переменных. Суть его в том, что высоко коррелированные объясняющие переменные устраняются из регрессии, и она заново оценивается. Критерием отбора переменных, подлежащих исключению, является коэффициент корреляции. Есть еще один способ решения данной проблемы, который заключается в замене переменных, которым присуща мультиколлинеарность, их линейной комбинацией. Этим весь список не исчерпывается, есть еще пошаговая регрессия и другие методы. К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель. Видео:Множественная степенная регрессияСкачать Линейная регрессия плюсов на Хабре Итак, довольно теоретического багажа и можно строить саму модель. Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии. Загружает данные из tsv файла. points — Рейтинг статьи reads — Число просмотров. comm — Число комментариев. faves — Добавлено в закладки. fb — Поделились в социальных сетях (fb + vk). bytes — Длина в байтах. Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных. Теперь собственно сама модель, используем функцию lm . В первой строке мы задаем параметры линейной регрессии. Строка points . определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points reads , набор переменных — points Перейдем теперь к расшифровке полученных результатов. Intercept — Если у нас модель представлена в виде , то тогда — точка пересечения прямой с осью координат, или intercept . R-squared — Коэффициент детерминации указывает насколько тесной является связь между факторами регрессии и зависимой переменной, это соотношение объясненных сумм квадратов возмущений, к необъясненным. Чем ближе к 1, тем ярче выражена зависимость. Adjusted R-squared — Проблема с в том, что он по любому растет с числом факторов, поэтому высокое значение данного коэффициента может быть обманчивым, когда в модели присутствует множество факторов. Для того, чтобы изъять из коэффициента корреляции данное свойство был придуман скорректированный коэффициент детерминации . F-statistic — Используется для оценки значимости модели регрессии в целом, является соотношением объяснимой дисперсии, к необъяснимой. Если модель линейной регрессии построена удачно, то она объясняет значительную часть дисперсии, оставляя в знаменателе малую часть. Чем больше значение параметра — тем лучше. t value — Критерий, основанный на t распределении Стьюдента . Значение параметра в линейной регрессии указывает на значимость фактора, принято считать, что при t > 2 фактор является значимым для модели. p value — Это вероятность истинности нуль гипотезы, которая гласит, что независимые переменные не объясняют динамику зависимой переменной. Если значение p value ниже порогового уровня (.05 или .01 для самых взыскательных), то нуль гипотеза ложная. Чем ниже — тем лучше. Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями. Проверим значения параметров линейной регрессии. Как видим в целом отзывчивость модели возросла, параметры подтянулись и стали более шелковистыми , F-статистика выросла, так же как и скорректированный коэффициент детерминации . Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений. И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана. Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать В заключение Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки. Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так. 📺 Видео Эконометрика Линейная регрессия и корреляцияСкачать Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать Эконометрика. Множественная регрессия и корреляция.Скачать Пример проверки гипотезы о незначимости регрессииСкачать Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства