Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Изопроцессы в газах.
- Изобарный процесс.
- Изохорный процесс.
- Изотермический процесс.
- Изоэнтропийный процесс.
- Изопроцессы
- Изотермический процесс
- Графики изотермического процесса
- Изобарный процесс
- Графики изобарного процесса
- Изохорный процесс
- Графики изохорного процесса
- 🔥 Видео
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 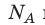
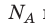
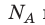
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
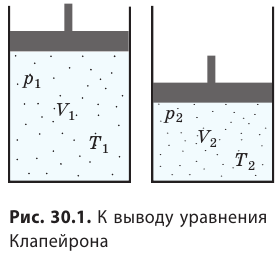
Уравнение Клапейрона
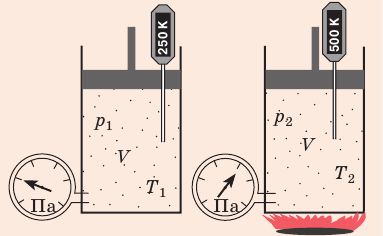
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (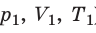
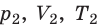
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 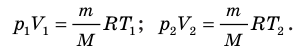
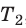
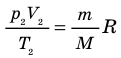
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
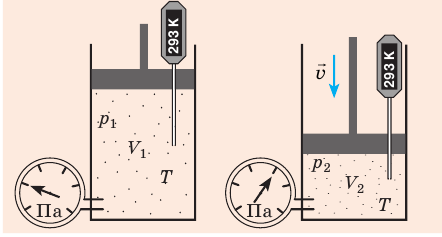
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (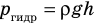
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (
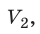
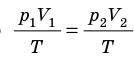
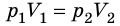
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 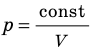
Какой процесс называют изобарным. Закон Гей-Люссака
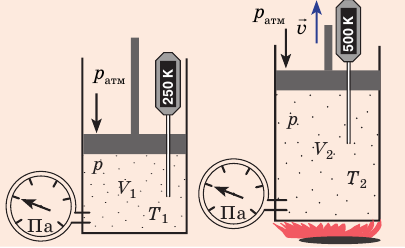
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (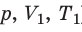
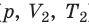
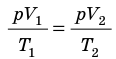
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (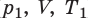
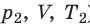
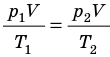
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 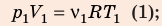
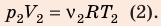

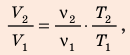
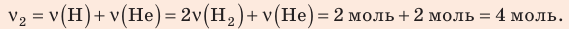
Ответ: примерно в 2,7 раза.
Пример №2
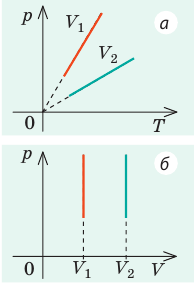
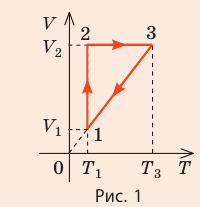
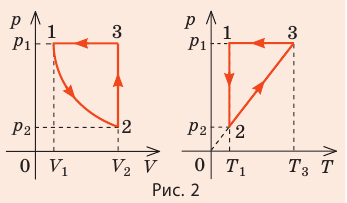
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Решение графических задач на тему Газовые законыСкачать

Изопроцессы в газах.
Изопроцессами называются процессы, протекающие при неизменном значении одного из параметров: давления (p), объема (V), температуры (T).
Изопроцессами в газах являются термодинамические процессы, на протяжении течения которых количество вещества и давление, объём, температура либо энтропия не поддаются изменениям. Таким образом, при изобарном процессе не изменяется давление, при изохорном — объём, при изотермическом — температура, при изоэнтропийном — энтропия (к примеру, обратимый адиабатический процесс). И линии, которые отображают перечисленные процессы на некой термодинамической диаграмме, называют, соответственно, изобара, изохора, изотерма и адиабата. Все эти изопроцессы являются частными случаями политропного процесса.
В идеальном газе эти процессы подчиняются газовым законам.
Газовыми законами называются количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра.
Видео:Связь между давлением, объёмом и температурой газаСкачать

Изобарный процесс.
Изобарный (или изобарический) процесс — это изменение термодинамической системы с условием не изменения давления (P = const). Изобарой называют линию, которая отображает изобарический процесс на графике. Этот процесс описывает закон Гей-Люссака.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Изохорный процесс.
Изохорный (или изохорический) процесс — это изменение термодинамической системы с условием не изменения объема (V = const). Изохорой называют линию, которая отображает изохорический процесс на графике. Этот процесс описывает закон Шарля.
Видео:Зависимость объёма газа данной массы от его температурыСкачать

Изотермический процесс.
Изотермический процесс — это изменение термодинамической системы с условием не изменения температуры (T = const). Изотермой называют линию, которая отображает изотермический процесс на графике. Этот процесс описывает закон Бойля-Мариотта.
Видео:Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Изоэнтропийный процесс.
Изоэнтропийный процесс — это изменение термодинамической системы с условием не изменения энтропии (S = const). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:
где γ — показатель адиабаты, определяемый типом газа.
Видео:Физика 10 класс. Газовые законыСкачать

Изопроцессы
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.
На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:
• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:
Данное утверждение называется законом Бойля — Мариотта.
Записав закон Бойля — Мариотта в виде
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой.
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1 .
Рис. 1. Изотерма на -диаграмме
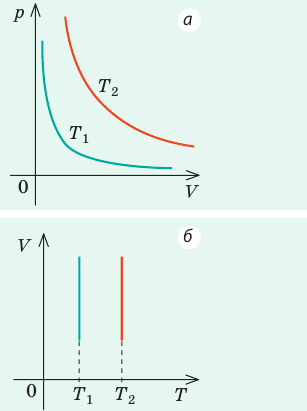
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2 ). Первый процесс идёт при температуре , второй — при температуре .
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — p_1′ alt=’p_2 > p_1′ /> . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, T_1′ alt=’T_2 > T_1′ /> .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3 ):
Рис. 3. Изотермы на и -диаграммах
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Видео:Изопроцессы. Графики изопроцессов. Закон Дальтона. 2 часть. 10 класс.Скачать

Графики изобарного процесса
График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4 ):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5 ):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, p_1′ alt=’p_2 > p_1′ /> .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6 ):
Рис. 6. Изобары на и -диаграммах
Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
Ввиду произвольности выбора состояний мы приходим к закону Шарля:
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Графики изохорного процесса
График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7 ):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8 ):
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, V_1′ alt=’V_2 > V_1′ /> .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9 ):
Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
🔥 Видео
Уравнение состояния идеального газаСкачать

Физика. МКТ: Графики газовых процессов. Центр онлайн-обучения «Фоксфорд»Скачать

Температура и тепловое равновесие. Определение температуры | Физика 10 класс #30 | ИнфоурокСкачать

Уравнение состояния идеального газа. Газовые законыСкачать

Урок 163. Задачи на графики процессов в газахСкачать

Физика. 10 класс. Изопроцессы. Графики изопроцессов. Закон Дальтона /26.11.2020/Скачать

график идеальный газСкачать

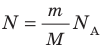
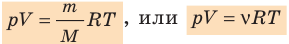
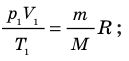
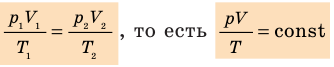
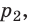
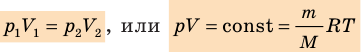

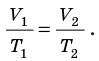
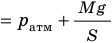
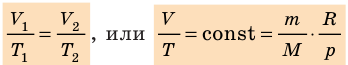
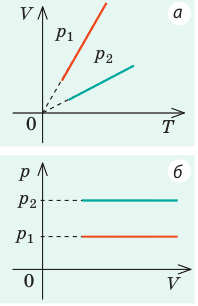

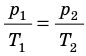
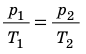
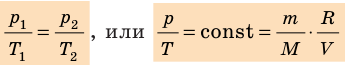

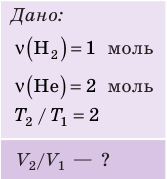
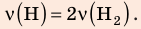

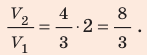
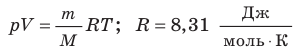 — универсальная газовая постоянная.
— универсальная газовая постоянная.