Процедура линеаризации полиномиальных уравнений регрессии представлена логарифмированием (3 видео)

Линеаризация нелинейных моделей регрессии

Вы будете перенаправлены на Автор24

Содержание

Понятие регрессии
Нелинейные модели регрессии
Готовые работы на аналогичную тему
Линеаризация нелинейных моделей регрессии
Тема 11. Нелинейные регрессии и их линеаризация
Методы линеаризации функции регрессии
🎬 Видео

Видео:Множественная регрессия в ExcelСкачать

Понятие регрессии

Регрессия – это односторонняя зависимость, которая устанавливает соответствие между случайными величинам.

Сущность регрессии заключается в том, чтобы через математическое выражение установить связь между зависимой и независимыми переменными. Ее отличительной особенностью от функциональной зависимости является тот факт, что каждому значению независимой соответствует одно определенное значение зависимой. В регрессионной связи одной и той же величине могут соответствовать абсолютно разные величины.

Впервые регрессию стали использовать в конце девятнадцатого века. Она была применена для установления зависимости между параметрами человека. Регрессию смогли перенести на плоскость. Точки легли на одну прямую, поэтому ее назвали линейной.

Построение линейной регрессии подразумевает, что ошибок в ней нет. Тогда распределение величин происходит под влиянием нормального закона. То есть, среднее значение равно нулю, а отклонение постоянно.

Чтобы вычислить параметры модели часто применяют программное обеспечение. Оно позволяет обрабатывать большие массивы информации с минимальными ошибками. Существуют специальные методы, позволяющие проверить величину отклонения. Ошибки необходимы для того, чтобы находить доверительные интервалы и проверять выдвинутые в начале исследования гипотезы. Например, в статистике используется критерий Стьюдента, позволяющий сопоставить средние значения двух выборок.

Самое простое представление регрессии состоит из зависимости между соотношениями случайной и независимой величины. Этот подход необходим для установления функциональной связи, если величины не случайны. В практической деятельности коэффициенты неизвестны, поэтому их исследуют с помощью экспериментальных данных.

Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать

Нелинейные модели регрессии

Построение нелинейной регрессии осуществляется для того, чтобы провести анализ. В нем экспериментальные данные записываются в функциональную зависимость, описывающей нелинейную комбинацию, представляющую модель, которая зависит от одной или нескольких переменных. Чтобы приблизить полученные данные к практическим величинам используется метод последовательных приближений.

Готовые работы на аналогичную тему

Этот метод заключается в следующем. Исследователем определяются корни уравнения или системы уравнений для того, чтобы упростить решаемую задачу, либо определить неизвестные параметры.

Структура нелинейной регрессии состоит из независимых и зависимых переменных. Для каждой переменной устанавливается случайная величина со средним значением. Погрешность может появиться, но есть ее обрабатывать, то она выйдет за пределы модели. В случае, если переменные не свободны, то модель становится ошибочной, поэтому для исследования становится непригодной.

Вот некоторые примеры нелинейных функций:

Показательные.
Логарифмические.
Тригонометрические.
Степенные.
Функция Гаусса.
Кривые Лоуренца.

В некоторых случаях регрессионный анализ может быть сведен к линейному, но данный способ должен применяться с осторожностью. Чтобы получить наилучший вариант расчета применяются оптимизационные алгоритмы. На практике могут применяться оценочные значения совместно с методиками оптимизации. В результате надо найти глобальный минимум суммы квадратов.

Нелинейная регрессия чаще всего применяется, как статистика линейной. Это позволяет сместить статистику, поэтому полученные данные интерпретируются с осторожностью.

Видео:Полиномиальная регрессияСкачать

Линеаризация нелинейных моделей регрессии

Линеаризация – это преобразование. Оно осуществляется для того, чтобы упростить определенные модели и вычисления. Например, применение логарифма к обеим частям линейной регрессии позволяет оценить неизвестные параметры более простым способом.

Но использование нелинейного изменения уравнения требует осторожности. Это связано с тем, что данные будут изменяться. Поэтому появятся ошибки модели. Их интерпретация может привести к ошибочному суждению о гипотезе. Обычно в нелинейных уравнениях используется модель Гаусса для исследования ошибок, что необходимо учитывать при проверке.

В которых случаях применяется уравнение Лайнуивер – Берк, либо обобщенная линейная модель.

Чтобы уточнить построенную модель и снизить вероятность ошибок, независимая переменная разбивается на классы. Вследствие этого линейная регрессия разбивается посегментно. Она может дать результат, в котором будет видно, как ведет себя параметр в зависимом положении. Отображение изменений производится графически.

То есть сущность линеаризации заключается в том, что исследователь применяет особые методики для того, чтобы провести преобразования исходных данных. Это позволяет исследовать нелинейную зависимость. Переменные нелинейного уравнения преобразуются с помощью специальных методик в линейные. Это может привести к ошибкам, что необходимо учитывать в процессе преобразования уравнения. Метод может быть опасным, так как влияет на результат вычислений.

Сущность метода заключается в том, что нелинейные переменные заменяются линейными. Регрессия сводится к линейной. Такой подход часто используется для полиномов. Далее применяются известные и простые оценки исследования линейных регрессии. Но изменение полиномов должно так же проводиться с осторожностью. Чем выше порядок полинома, тем сложнее удержаться в рамках реалистичной интерпретации коэффициентов регрессии.

В логарифмических моделях составляется линейная модель с новыми переменными. Оценка результата происходит с помощью метода наименьших квадратов. Эта методика подходит для исследования кривых спроса и предложения, производственных функций, кривых освоения связи между трудоемкостью и производственными масштабами. Такой подход актуален при запуске новых видов продукции.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Тема 11. Нелинейные регрессии и их линеаризация

Аннотация.Данная тема раскрывает особенности построения нелинейных моделей регрессии.

Ключевые слова.Нелинейная регрессия, индекс корреляции, коэффициент эластичности, подход Бокса-Кокса.

Методические рекомендации по изучению темы

· Тема содержит лекционную часть, где даются общие представления по теме.

· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.

· Для проверки усвоения темы имеется тест для самоконтроля.

· Для подготовки к экзамену имеется контрольный тест.

Рекомендуемые информационные ресурсы:

2. Эконометрика: [Электронный ресурс] Учеб. пособие / А.И. Новиков. — 3-e изд., испр. и доп. — М.: ИНФРА-М, 2014. — 272 с.: (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 41-45.

3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 564 с.

(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 383-399.

4. Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. — М.: НИЦ ИНФРА-М; Мн.: Нов. знание, 2014. — 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С.172-174.

Глоссарий

Бокса-Кокса подход – способ подбора линеаризующего преобразования.

Индекс корреляции—показатель корреляции, который определяется для нелинейных регрессий.

Коэффициент эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 процент.

Линеаризация нелинейных моделей – процедура, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований.

Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду.

Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции.

Вопросы для изучения

1. Классы и виды нелинейных регрессий.

2. Линеаризация нелинейных моделей. Выбор формы модели.

3. Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса).

Классы и виды нелинейных регрессий. Различают два класса нелинейных регрессий: регрессии, нелинейные относительно включенных в анализ объясняющих переменных; регрессии, нелинейные по оцениваемым параметрам. Нелинейная модель, внутренне линейная, с помощью преобразований может быть приведена к линейному виду. Нелинейная модель, внутренне нелинейная, не может быть сведена к линейной функции. При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации.

Линеаризация нелинейных моделей. Выбор формы модели. В нелинейных зависимостях, не являющихся классическими полиномами, обязательно проводится предварительная линеаризация, которая заключается в преобразовании или переменных, или параметров модели, или в комбинации этих преобразований. Рассмотрим некоторые классы таких зависимостей.

Рис. 11.1. Способы линеаризации

Замена переменных заключается в замене нелинейных объясняющих переменных новыми линейными переменными и сведении нелинейной регрессии к линейной. Логарифмирование обеих частей уравнения применяется обычно, когда мультипликативную модель необходимо привести к линейному виду. К классу степенных функций относятся: кривые спроса и предложения, производственная функция Кобба-Дугласа, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида изделий, зависимость валового национального дохода от уровня занятости.

Индекс корреляции. Подбор линеаризующего преобразования (подход Бокса-Кокса). Любое уравнение нелинейной регрессии, как и линейной зависимости, дополняется показателем корреляции, который в данном случае называется индексом корреляции:

Здесь — общая дисперсия результативного признака y, — остаточная дисперсия, определяемая по уравнению нелинейной регрессии . По-другому можно записать так:

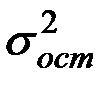
Следует обратить внимание на то, что разности в соответствующих суммах и берутся не в преобразованных, а в исходных значениях результативного признака. Иначе говоря, при вычислении этих сумм следует использовать не преобразованные (линеаризованные) зависимости, а именно исходные нелинейные уравнения регрессии. Величина R находится в границах , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.

Если разные модели используют разные функциональные формы для зависимой переменной, то проблема выбора модели становится более сложной, так как нельзя непосредственно сравнивать коэффициенты R 2 или суммы квадратов отклонений. Например, нельзя сравнивать эти статистики для линейного и логарифмического вариантов. Пусть в линейной модели в качестве зависимой переменной используется заработок, а в нелинейной – логарифм заработка. Тогда R 2 в одном уравнении измеряет объясненную регрессией долю дисперсии заработка, а в другом — объясненную регрессией долю дисперсии логарифма заработка. В случае, если значения R 2 для двух моделей близки друг к другу, проблема выбора усложняется. Здесь следует использовать тест Бокса – Кокса. При сравнении моделей с использованием в качестве зависимой переменной y и lny проводится такое преобразование масштаба наблюдений y, при котором можно непосредственно сравнивать суммы квадратов отклонений в линейной и логарифмической моделях. Здесь выполняются следующие шаги. Вычисляется среднее геометрическое значений y в выборке. Оно совпадает с экспонентой среднего арифметического логарифмов y. Все значения y пересчитываются делением на среднее геометрическое, получаем значения y*. Оцениваются две регрессии: для линейной модели с использованием y* в качестве зависимой переменной и для логарифмической модели с использованием ln y* вместо ln y. Во всех других отношениях модели должны оставаться неизменными. Теперь значения СКО для двух регрессий сравнимы, и модель с меньшей остаточной СКО обеспечивает лучшее соответствие исходным данным. Для проверки, обеспечивает ли одна из моделей значимо лучшее соответствие, можно вычислить величину (n/2)lnz, где z – отношение значений остаточной СКО в перечисленных регрессиях. Эта статистика имеет распределение хи – квадрат с одной степенью свободы. Если она превышает критическое значение при выбранном уровне значимости α, то делается вывод о наличии значимой разницы в качестве оценивания.

Величина коэффициента эластичности показывает, на сколько процентов изменится результативный признак Y, если факторный признак изменится на 1 %:

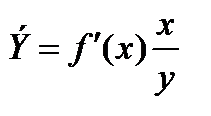
В заключение приведем формулы расчета коэффициентов эластичности для наиболее распространенных уравнений регрессии:

Вид уравнения регрессии	Коэффициент эластичности

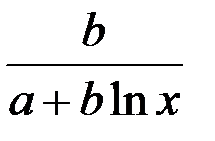Вопросы и задания для самоконтроля

1. Какие модели являются нелинейными относительно: а) включаемых переменных; б) оцениваемых параметров?

2. Какие преобразования используются для линеаризации нелинейных моделей?

3. Чем отличается применение МНК к моделям, нелинейным относительно включаемых переменных, от применения к моделям, нелинейным по оцениваемым параметрам?

4. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?

5. Какие показатели корреляции используются при нелинейных соотношениях рассматриваемых признаков?

6. В каких случаях используют обратные и степенные модели?

Задача 1.По группе предприятий, производящих однородную продукцию известно, как зависит себестоимость единицы продукции (Y) от факторов, приведенных в таблице:

Признак-фактор	Уравнение парной регрессии	Среднее значение фактора
Объем производства, млн. руб.
Трудоемкость единицы продукции, чел/час
Оптовая цена за 1т энергоносителя, , млн. руб.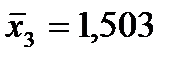
Доля прибыли, изымаемая государством, ,%

1) определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат;

2) ранжировать факторы по силе влияния на результат.

Задача 2. По группе из 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции (тыс. руб) от уровня технической оснащенности (тыс. руб.)

Доля остаточной дисперсии в общей составила 0,19.

1) определить коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.;

2) вычислить индекс корреляции;

3) оценить значимость уравнения регрессии с помощью критерия.

Видео:Математика #1 | Корреляция и регрессияСкачать

Методы линеаризации функции регрессии

Один из подходов оценки параметров нелинейных моделей состоит в линеаризации модели. Линеаризация модели заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. В рамках этого подхода различают два класса нелинейных регрессионных моделей, допускающих линеаризацию: а) модели, нелинейные относительно включенных в модель переменных, но линейных по оцениваемым параметрам; б) модели, нелинейные по оцениваемым параметрам.

Примером нелинейной регрессии, но линейной по оцениваемым параметрам, могут служить следующие функции: полиномы различных степеней, например

;

К нелинейным регрессионным моделям, нелинейным по оцениваемым параметрам, относятся: степенная функция

;

Нелинейная регрессионная модель с линейно включенными в нее параметрами не таит каких-либо сложностей в оценке ее параметров. Введение новых переменных позволяет свести её к линейной модели, для оценки параметров которой можно использовать обычный МНК. Так, например, если нужно оценить параметры регрессионной модели

то вводя новые переменные , , получим линейную модель

параметры которой находятся обычным МНК.

Следует, однако, отметить и недостаток такой замены переменных, связанный с тем, что оценки параметров получаются не из условия минимизации суммы квадратов отклонений для исходной переменной, а из условия минимизации суммы квадратов отклонений для новых переменных, что не одно и то же. К тому же такое преобразование искажает исходные предпосылки МНК, поскольку новые объясняющие переменные, вообще говоря, будут зависимыми. В связи с этим необходимо определенное уточнение полученных оценок.

Более сложной проблемой является нелинейность модели по параметрам, т.к. линеаризация достигается при помощи более сложных преобразований. Например, приведенную выше степенную модель при помощи логарифмического преобразования можно привести к линейному виду

К этой модели уже можно применить обычный МНК. Однако следует подчеркнуть, что критерии значимости и интервальные оценки параметров, применяемые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в такой модели имел логарифм случайного отклонения (т.е. , а вовсе не e. Другими словами, случайное отклонение e должно иметь логарифмически нормальное распределение.

Заметим попутно, что к модели

рассматриваемой в качестве альтернативной к уже рассмотренной, изложенный метод исследования уже непригоден, т.к. ее нельзя привести к линейному виду. В этом случае можно использовать только численные методы нелинейной оптимизации.

Отметим ещё, что при построении нелинейных уравнений более остро, чем в линейном случае, стоит проблема правильной оценки формы зависимости между переменными. Неточности при выборе формы оцениваемой функции существенно сказываются на качестве отдельных параметров уравнений регрессии и, соответственно, на адекватности всей модели в целом (проблема спецификации).

§6.2. ОПИСАНИЕ ОСНОВНЫХ НЕЛИНЕЙНЫХ
РЕГРЕССИОННЫХ МОДЕЛЕЙ

Полиномиальная модель

(6.3)

называется полиномиальной моделью. Как показывает опыт, среди полиномиальных моделей чаще всего используется параболическая и кубическая модели. Ограничение использования полиномов более высоких степеней связана с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.

(6.4)

может отражать зависимость между объемом выпуска и средними или предельными издержками; или между расходами на рекламу и прибыль и т.д. Параболическая модель целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную и наоборот. Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболической модели становятся трудно интерпретируемыми, поэтому форма связи заменяется другой нелинейной моделью (например, степенной).

При b₁>0 и b₂ 0). Функция (6.7) может отражать также зависимость объёма выпуска Y от использования ресурса X (производственная функция), в которой 0