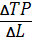Производственная функция — экономико-математическая количественная зависимость между величиной выпуска (объемом продукции фирмы) и факторами производства, такими как затраты ресурсов, уровень технологий.
Наиболее известные примеры производственных функций: функция Кобба-Дугласа вида $Y=Acdot L^cdot K^$, в которой предполагается постоянные эластичности ($alpha$ и $beta$) выпуска по факторам производства $K$ и $L$ соответственно (капитал и трудовые затраты); линейная производственная функция: $Y=aK+bL$, функция Леонтьева и т.д.
В этом разделе вы найдете подробно решенные задачи, касающиеся производственной функции (в том числе модели Кобба-Дугласа).
Видео:Построение производственной функции Кобба-ДугласаСкачать
Производственная функция: задачи с решениями
Задача 1. Производственная функция коммерческого предприятия имеет вид $f=10sqrtcdot sqrt$, где $f$ — товарооборот, тыс. руб.; $x_1$ — производственная площадь, м ; $x_2$ — численность работников, сотни человек. Рассмотрите изокванту уровня $y_0$ и найдите точку $C_1$ и точку $C_2$. Сделайте вывод о возможности замены ресурсов. Полученные результаты изобразите графически.
Задача 2. Исходные данные. Фирма, производящая продукцию при заданной рынком системе цен по технологии, отображающейся производственной функцией $Q = 20 L^$, может продавать любой объем своей продукции по цене Р = 6. Фирма может использовать любое количество труда по цене w = 40.
1. Какой тип производственной функции представлен в задании? В чем ее особенность? Приведите пример подобного производства. Изобразите график заданной производственной функции, а также графики среднего и предельного продуктов переменного фактора (труда).
2. На основе представленных данных выведите функции общих, средних и предельных затрат фирмы, функцию индивидуального предложения фирмы и определите объем предложения при заданной цене блага.
3. Дайте характеристику статуса фирмы на товарном и факторном рынках в представленном примере. Раскройте различия в поведении фирмы-совершенного конкурента и фирмы-монопсониста на рынке фактора. Приведите примеры подобного поведения фирм на рынке труда.
4. Выведите функцию спроса фирмы на труд, если цена блага P = 6 и остается неизменной. Определите объем спроса на труд при w = 40. Решение сопроводите графиком. Укажите несколько факторов (не менее трех), влияющих на спрос фирмы на труд.
Задача 3. Процесс производства некоторого товара описывается с помощью производственной функции $q=f(x_1, x_2)=54x_1^x_2^$. Для плана (2,5) найти первый второй предельные продукты. Дайте экономическую интерпретацию полученным результатам. Выясните, характеризуется ли ПФ той или иной разновидностью эффекта масштаба. Предполагая, что производитель приобретает ресурсы по ценам (2,7) найдите функцию переменных издержек $C_v(q)$.
Видео:7.2.3. Связь эффекта масштаба с производственными функциямиСкачать
Модель Кобба-Дугласа: задачи с решениями
Задача 4. Производственная функция фирмы имеет вид: $Q = К^cdot L^$. Предположим, что в день затрачивается 4 часа труда (L = 4) и 4 часа работы машин (К = 4).
Определить:
1) максимальное количество выпускаемой продукции;
2) средний продукт труда;
3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?
Задача 5. Задана производственная функция Кобба-Дугласа
Изобразить изокванту, соответствующую плану (36,27). Какое количество продукта выпускается при этом плане?
Найти первый, второй предельные продукты для плана (36,27) и дать экономическую интерпретацию полученным результатам.
Каким эффектом от расширения масштабов производства характеризуется производственная функция
Каковы затраты производителя на покупку ресурсов при плане производства (36,27) и заданном векторе цен на ресурсы (3,4)?
Найти самый дешевый (оптимальный) план по ресурсам, обеспечивающий выпуск такого же количества продукции, что и для плана (36,27). Найти аналитически решение этой задачи
методом Лагранжа
методом подстановки.
Сделать геометрическую иллюстрацию решения задачи, изобразив ОДР и целевую функцию линиями уровня.
Задача 6. На основании представленных в таблице ниже данных построить ПФ типа Кобба-Дугласа. Сделать прогноз объема производства отрасли на 2000 год, если планируются увеличение основных фондов на 20% и одновременное уменьшение трудовых ресурсов на 5% относительно предыдущего года. Пусть заданы агрегированные основные показатели некоторой отрасли за четыре года:
Задача 7. Для построенной в самостоятельной работе производственной функции рассчитать предельные производительности, предельные нормы замещения ресурсов в 1993 и 1999 годах, сделать сравнительный экономический анализ. При расчетах предположить, что ресурсы в исследуемом году заданы, объем производства вычисляется.
Задача 8. Пусть производственная функция имеет вид $Y = 0.94 cdot K^cdot L^$. Для базового года $K_0 = 727$ млн ден. ед., $L_0 = 97.7$ тыс. человек. Для отчётного года $K_1 = 977$ млн ден. ед., $L_1 = 127.7$ тыс. человек. Подсчитать индексы изменения характеристик, масштаб и экономическую эффективность производства. Дать экономическую интерпретацию.
Задача 9. Производственная функция фирмы, выпускающая линолеум, имеет вид $Y=177 K^ L^$. Здесь $Y$ – сотни м*м, $K$ – тыс. ден. ед., $L$ – сотня рабочих (сот. р.).
Стоимость ресурсов W=5,13 тыс. ден. ед./сот. раб.
q = 10 тыс. ден. ед./тыс. ден. ед.
Издержки производства ограничены суммой C = 1770 тыс. ден. ед.
Найти максимальный выпуск продукции, оптимальное количество рабочих и стоимость капитальных фондов.
Построить график изокванты и изокосты. Отметить оптимальную точку.
Оценить, как изменится выпуск продукции, если:
а) увеличить заработную плату на 8%;
б) уменьшить цену на фонды в два раза;
в) ввести дополнительные инвестиции в производство в количестве 57,7 тыс. ден. ед.
Задача 10. Найти объем продукции, произведенной за период $[0;52]$, если функция Кобба-Дугласа имеет вид: $f(t)=(364+7t)e ^$
Задача 11. 1. Выпуск продукции фирмой описывается функцией Кобба-Дугласа $Y=AK^L^$. Ставка заработной платы равна $p_L$, норма процента на используемый капитал — $p_K$.
2. По заданному уровню выпуска продукции $Y$ определить объемы факторов $K$ и $L$, при которых общие издержки будут минимальны, и величину этих издержек.
3. По известной величине общих издержек $TC$ определить объем факторов $K$ и $L$, обеспечивающие максимальный выпуск продукции, и соответствующий объем выпуска.
Задача 12. На основании следующих данных построить производственную функцию Кобба-Дугласа.
Здесь $Y_i$ — производственный национальный доход (млрд. руб.), $K_i$ — среднегодовые основные производственные фонды (млрд. руб.), $L_i$ — среднегодовая численность занятых в материальном производстве (млн. чел.). Имеется прогноз на 1997 год: основных производственных фондов $K_cdot N$ млн. руб. и трудовых ресурсов $L_cdot N$, где $N$ (номер) млн. чел. На основании полученной производственной функции сделать точечный прогноз национального дохода на 1997 год.
Задача 13. Производственная функция задается формулой $Q = 150 K^L^$, где Q — выпуск, K – капитал, L — труд.
Найти:
a) Предельные продукты труда и капитала при K=16, L=125.
б) Коэффициенты эластичности выпуска по труду и капиталу и объяснить их экономический смысл для полученных значений.
Видео:6.2.1. Производственная функцияСкачать
3.6 Производственная функция
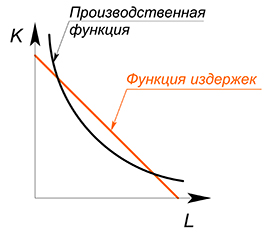
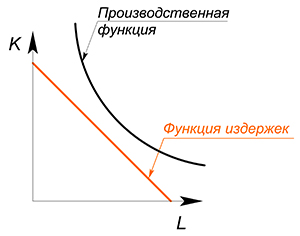
Производственная функция показывает налучшую технологическую зависимость между количеством используемых ресурсов и объемом выпуска.
Из производственной функции можно вывести функцию издержек.
Пример 1
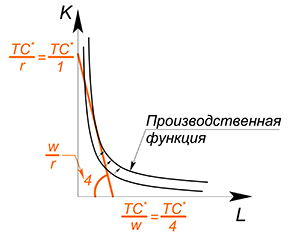
Дано: $Q= L cdot K$, $w=4$, $r=1$, найти функцию общих издержек.
В данном случае можно или минимизировать издержки при выбранном уровне $Q$, или максимизировать объем выпуска при данном уровне издержек.
Воспользуемся методом 2:
Как уже не раз случалось, мы опять встречаем функцию, зависящую от двух переменных. Зафиксируем $TC$, выразим $L$ через $K$:
Что касается производственной функции — зафиксируем $Q$, выразим $L$ через $K$:
Имеем схожую ситуацию с задачей максимизации полезности, только в данном случае у нас цель — максимизировать объем выпускаемой продукции:
Возьмем производную обеих функций по $L$, найдем точку, в которой они равны, найдем точку касания графиков
(Почему именно касания? Если бы мы выбрали более низкий уровень $Q^*$, то мы получили бы более низкую производственную функцию, произвели бы меньше продукции с теми же издержками:
Если мы бы выбрали слишком высокий уровень $Q$, то данный объем производства был бы недостижим при данном уровне издержек:
Подставим в производственную функцию, выразим $K$:
Теперь подставим $L$ и $K$ в функцию издержек, $Q$ снова является переменной:
Пример 2
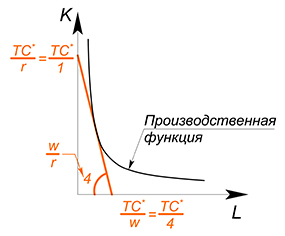
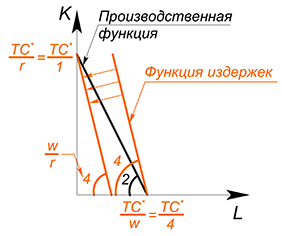
Производственная функция является линейной: $Q=2L+K$, $w=4$, $r=1$, $TC(Q)-?$
Действовать будем в целом аналогично предыдущему варианту, но в этот раз попробуем использовать метод 1: будем минимизировать издержки при выбранном уровне $Q$:
Имеем 2 линейные функции, будем двигать функцию издержек вниз, пока она не достигнет оптимального положения:
(Если мы выберем более высокий уровень издержек, то вступим нерационально — такой же объем выпуска при больших издержках. Зачем? Если выбрать более низкий уровень издержек, то невозможно будет произвести нужный объем продукции) .
Оптимальное положение будет достигнуто в точке, где количество капитала максимально, а труда равно нулю. Тогда:
Эффект масштаба показывает во сколько раз изменится $Q$ после увеличения всех используемых ресурсов в одинаковое число раз $t$ по сравнению с первоначальным $Q$, увеличенным в $t$ раз.
Если $Q_(tL;tK) > tQ(L;K)$, то эффект масштаба положительный, если $Q_(tL;tK)=tQ(L;K)$, то постоянный, если $Q_(tL;tK) 1$, следовательно эффект масштаба положительный
TP — total product (он же Q), общий продукт труда — показывает зависимость объема выпуска продукции от количества переменного ресурса при прочих равных условиях.
i участок — функция растет ускоряющимся темпом, при найме каждого последующего работника объем выпуска увеличивается на все большую и большую величину;
ii участок — функция растет замедляющимся темпом, при найме каждого дополнительного работника объем выпуска увеличивается на все меньшую величину;
iii участок — $TP$ убывает. При производстве товара может наступить такой момент, когда дополнительная единица переменного ресурса (труда обычно) уже не способствует увеличению производимой продукции. Дополнительно нанятый работник может только мешать. Например, если у нас имеется всего один станок, и мы наняли 50 рабочих, то они будут только мешать друг другу, стопившись у этого единственного механизма.
$AP_(L)$ average product, средний продукт (труда) — показывает, сколько в среднем единиц продукции приходится на одну единицу переменного ресурса:
Геометрический смысл среднего среднего продукта труда такой же как и у других средних величин — тангенс угла наклона луча, проведенного из начала координат (секущей) к точке на графике общего продукта труда.
$MP_(L)$ — marginal product, предельный продукт (труда) — показывает прирост общего продукта при увеличении переменного ресурса на единицу.
В дискретном случае $MP_L=dfrac$.
Геометрический смысл предельного продукта в данном случае — тангенс угла наклона секущей, соединяющей точки $(L_1;TP_1)$ и $(L_2;TP_2)$.
Если ресурс бесконечно делим, то $MP_L=TP'(L)$
Геометрический смысл предельного продукта в этой ситуации — тангенс угла наклона касательной, проведенной к графику $TP$ в интересующей нас нас точке.
Пример 4
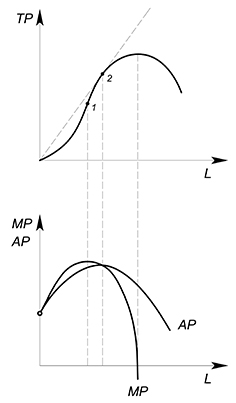
$Q(L)=30L-L^2$, найти $AP_L$, $MP_L$
Видео:11. Производная неявной функции примерыСкачать
ТЕМА 5. Технология. Производственный выбор
В процессе производства фирма объединяет необходимые ресурсы и выпускает продукт. Принимая решение о необходимом количестве ресурсов, предприниматель должен учитывать производительность и рыночную цену. Теория производства описывает процесс принятия рационального решения, т. е. как достичь максимума выпуска при данной технологии и рыночных ценах.
Технология. Процесс производства и факторы производства. Производственная функция. Свойства производственной функции. Краткосрочный и долгосрочный периоды в деятельности фирм. Производственная функция в краткосрочном периоде. Постоянные и переменные факторы производства. Общий, средний и предельный продукты, взаимосвязь между ними. Производство с одним переменным фактором. Закон убывающей предельной производительности. Стадии производства в краткосрочном периоде. Графическая модель производственной функции в коротком периоде,
Производственная функция в долгосрочном периоде. Производство с двумя переменными факторами. Графическая модель производственной функции в длительном периоде изокванты, карта изоквант. Предельная норма технологического замещения. Производственная функция Кобба — Дугласа и функция издержек. Техническая и экономическая эффективность. Оптимальная комбинация факторов производства. Взаимозаменяемость и взаимодополняемость факторов производства. Эффект масштаба производства; постоянный эффект масштаба, растущий и убывающий эффект масштаба.
ПЛАН ЛЕКЦИЙ
1 Процесс производства и факторы производства Техническая и экономическая эффективность.
2. Производственная функция.
3. Производственный выбор в краткосрочном периоде. Закон убывающей предельной производительности.
4. Производственный выбор в длительном периоде. Предельная норма технологического замещения.
ПЛАН СЕМИНАРА
1. Постоянные и переменные факторы производства Роль
временного периода.
2. Свойства производственных функций. Общий, средний и предельный
продукты.
3. Убывающая отдача переменного ресурса. Стадии производства.
4. Отдача от масштаба.
5 Взаимозаменяемость и взаимодополняемость факторов производства.
Основные понятия
Краткосрочный период— промежуток времени, в течение которого хотя бы один фактор производства остается фиксированным, т.е. постоянным. Те факторы, количество которых можно изменить, называются переменными.
Долгосрочный период — промежуток времени, в течение которого может быть изменено количество всех используемых факторов производства.
Производственная функция характеризует техническую зависимость между количеством применяемых ресурсов и объемом выпускаемой продукции в единицу времени. В теории производства используется двухфакторная производственная функция вида: Q = f (К, L), где Q — объем выпускаемой продукции, К — количество используемого капитала, L-количество труда.
Изокванта (линия равного выпуска) — множество точек, координат которых характеризуют минимальные количества труда и капитала, необходимые для создания данного объема продукции .
Графическим изображением производственной функции является карта изоквант — множество комбинаций производственных ресурсов, необходимых для выпуска различных определенных объемов продукции.
Предельная норма технологического (MRTS) другим (например, капитала трудом) показывает, от какого количества одного ресурса (капитала) можно отказаться, если увеличить количество другого ресурса (труда) на единицу. Предельная норму технологического замещения в каждой точке изокванты равна тангенсу угла наклона касательной к этой точке. То есть предельная норма технологического замещения капитала трудом MRTSLK =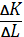 
= 
L
Закон убывающей предельной отдачи гласит, что эффективность использования любого ресурса ограничена. По мере замены одного ресурса другим (капитала трудом) отдача ресурса, количество которого возрастает (производительность труда), снижается. Действие закона убывающей предельной отдачи обусловливает убывание предельной нормы замещения вдоль изокванты, являющейся графические изображением производственной функции Кобба — Дугласа. Это производственная функция вида: Q=AK α L β , где 0
Равновесие производителядостигается в точке касания изокосты, т.е. т.е. условием равновесия является равенство MRTSLK=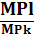 
= 
.
Отдача от масштаба возникает при изменении масштаба производства, т.е. при пропорциональном увеличении количества всех используемых ресурсов. Если при увеличении количества используемых ресурсов в k раз выпуск возрастает так же в k раз, то имеет место постоянная отдача от масштаба Если выпуск увеличивается больше, чем в k раз, то отдача от масштаба возрастает, если меньше — убывает.
Совокупный (общий) продукт — максимальный объем производства, который возможно получить при данном объеме используемых ресурсов.
Предельный продукт переменного фактора производства — это изменение совокупного продукта при увеличении количества используемого фактора на единицу: MPF= 
Например, предельный продукт труда показывает, насколько вырастет общий выпуск продукции при увеличении объема используемого труда на единицу: MPL=
Средний продукт переменного фактора — это объем производства в расчете на единицу переменного фактора. Например, средний продукт труда, APL=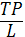 
, это производительность труда.
Динамика общего, среднего и предельного продуктов тесно связана и подчиняется закону убывающей предельной отдачи: пока предельный продукт возрастает, общий продукт растет увеличивающимся темпом (стадия возрастающей отдачи); когда предельный продукт начинает убывать, общий продукт растет уменьшающимся темпом (стадия убывающей от дачи); когда предельный продукт становится отрицательным, общий продукт начинает убывать (стадия отрицательной отдачи). График среднего продукта пересекает график предельного продукта в точке максимума среднего продукта. Максимальное значение среднего продукта достигается в точке, где луч, выходящий из начала координат, касается кривой общего продукта (APL= 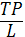=tgα; APL максимален в точке касания).
ТЕСТЫ
1. Графическим изображением двухфакторной производственной функции в общем случае является:
1) кривая средней производительности факторов,
2)кривая предельной производительности факторов;
3) карта кривых постоянного выпуска,
4) линия постоянной нормы технического замещения факторов;
5) линия бюджетного ограничения.
2. Если в коротком периоде достигнут максимальный объем производства, это означает, что:
1) средний и предельный продукты переменного фактора равны;
2) средний продукт достигает своего максимума, а предельный продукт равен кулю;
3) достигается максимум значения предельного продукта при минимальном значении среднего продукта;
4) предельный продукт становится равным нулю, а средний продукт убывает;
5) нет правильного ответа.
3. Дана производственная функция Q(L,К)=1/2L 0,8 К 0.9 — Какой экономией от масштаба она характеризуется?
1) возрастающей;
4) ничего определенного сказать нельзя,
4. Предельная норма технологического замещения труда капиталом равна 1/2. На сколько единиц необходимо увеличить использование капитала, если количество используемого труда сокращается на 6 единиц, а объем производства продукции остается прежним?
5) необходима дополнительна информация.
5. Убывающая предельная норма технологического замещения характерна:
2) кривой совокупного выпуска;
3) изокванты, выпуклой к началу координат(вогнутой);
4) изокванты, изображающей производственную функцию, для
которой характерна взаимозаменяемость ресурсов,
5) изокванты, изображающей производственную функцию, для
которой характерна взаимодополняемость ресурсов.
5. Производственная функция представлена в виде: Q=F(К,L1), где К- напитал,L — труд. Переменным фактором является только труд. В первой стадии производства для переменного фактора будет выполняться условие:
3)МР | если меньше, чем в n раз, то убывающая (отрицательная). Удвоим количество К и L; Q = 13 * (2L) *(2K)= 13 * 4 * KL. Объем производства Q увеличился в 4 раза, значит, отдача растущая.
Ответ: Растущая (положительная).
Каждая машина в таксомоторном парке работает в три смены. Тарифная ставка водителя, за смену w= 1, арендная плата за суточный прокат автомобиля r = 20 Издержки ТС = 690. Определите, сколько машин и водителей занято в сутки.
Решение:
Водитель и такси являются дополняющими ресурсами. Расходы таксопарка на функционирование одного такси в течение суток составляют: 3w+r = 23. Общие издержки таксопарка равны 690. Значит, величина 690/23= 30 дает нам количество машин, на каждой из которых в течение суток работает по три водителя.
ответ: Количество машин К = 30; водителей L = 90,
ЗАДАЧИ
№1
Найдите предельную и среднюю производительность капитали (МРК)
и АРк) по следующим данным:
| K |
| TP |
№2
Есть следующая информация о средней производительности работников в рублях в час:
| Количество работников |
| Производительность |
Какое количество работников наймет предприниматель при ставке заработной платы 25 руб. в час?
№3
Производственная функция задана уравнениемY= 19K 1/2 L 1/3 . Какова ее отдача от масштаба?
№ 4
Дана производственная функция Q = 4L 0,8 K 0,8 . Чему равно отношение предельной производительности труда к средней производительности труда?
№5
Дана производственная функция Q = 2L 0,2 K 0,8 . Чему равно отношение предельной производительности капитала к средней производительности капитала?
№6
Даны цены факторов производства: Рк = 20. Р1 = 10. Предельные продукты этих факторов на фирме в краткосрочном периоде составляют: МРk = 6, МРL = 4. Как использовать фирме факторы производства для максимизации объема производства в краткосрочном периоде?
№7
Каждый токарный станок на фирме работает в три смены. Тарифная ставка токаря за смену w = 2, плата за суточную аренду r = 30. Издержки ТС = 432. Определите, сколько станков и токарей занято в сутки.
№8
Объем выпуска задан производственной функцией Q = L 0,5 K 0,5 . Цена стала равна 40 долл. в день, цена труда 10 долл. вдень. Определите 1инимвльные затраты фирмы на выпуск 10 единиц продукции в день.
№9
Производственная фикция фирмы представлена в виде: Q(K,L) =L 1/5 6K 4/5 .Цены на капитальные и трудовые ресурсы составляют 20 и 35 руб. за единицу при величине затрат 7000. Определите количество используемого капитала и труда.
Производственная функция фирмы представлена в виде: Q(K,L) =L 0,25 5K 0,75 . Количество используемого капитала составляет 15 единиц, труда- 10. Определите цены на капитальные итрудовые ресурсы при объеме затрат равном 800, в условиях максимизации выпуска.
Ответы:
Тесты:1,3); 2. 4); 3,1); 4.3); 5.3), 6.2); 7.4).8.3): 9. 4). 10.3)
Задачи
| K | ||
| MPK | ||
| APK | 21,7 | 18,6 |
2 .Предприниматель наймет шесть работников
3 .Убывающая (отрицательная)
4. 4/5.
6. Увеличить использование труда и сократить — капитала.
7. Количество станков К — 12; токарей L = 36.
8. 400 долл. в день.
💡 Видео
Математический анализ, 15 урок, АссимптотыСкачать
Геометрический смысл производной | КасательнаяСкачать
Производящая функция чисел КаталанаСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Что такое производящая функция? ТеорияСкачать
Конформные отображенияСкачать
Лекция 2: Кинематика поступательного и вращательного движений.Скачать
Урок 7. Механическое движение. Основные определения кинематики.Скачать
КАК РАБОТАЮТ ЧИСЛА С ПЛАВАЮЩЕЙ ТОЧКОЙ | ОСНОВЫ ПРОГРАММИРОВАНИЯСкачать
Основные алгоритмические конструкции | Информатика 9 класс #14 | ИнфоурокСкачать
A.3.1 Понятие функцииСкачать
14. ПРОИЗВОДЯЩАЯ ФУНКЦИЯ 📚 Теория вероятностейСкачать
Вторая производная, Точки перегиба - Производная - Математический анализСкачать
ТММ - 4.5 2 часть. Построение кинематических диаграмм методом хорд.Скачать
Механическое движение. 9 класс.Скачать
