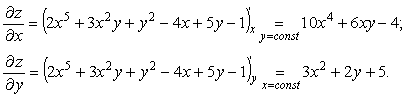Назначение сервиса . Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word .
- Решение онлайн
- Видеоинструкция
- Также решают
- Правила ввода функции, заданной в явном виде
- Правила ввода функции, заданной в неявном виде
- Частные производные функции нескольких переменных
- Частные производные для функции от нескольких переменных
- Что такое «частная производная»?
- Задачи с радикалами и многочленами
- Задача № 1
- Задача № 2
- Нюансы решения
- Задачи с тригонометрическими функциями и логарифмами
- Задача № 1
- Задача № 2
- Нюансы решения
- Задачи с показательными функциями и логарифмами
- Задача № 1
- Задача № 2
- Нюансы решения
- Задачи с тригонометрической функция и функцией с тремя переменными
- Задача № 1
- Задача № 2
- Нюансы решения
- Ключевые моменты
- Примеры решений задач: функции нескольких переменных
- Примеры: область определения ФНП
- Примеры: частные производные ФНП
- Градиент, производная по направлению
- Касательная плоскость и нормаль
- Экстремумы функции нескольких переменных
- Приближенные вычисления
- Ряд Тэйлора
- Наибольшее и наименьшее значение в области
- Решение контрольной
- Помощь с решением заданий
Правила ввода функции, заданной в явном виде
- Примеры
x 2 +xy ≡ x^2+x*y .
cos 2 (2x+y) ≡ (cos(2*x+y))^2≡ (x-y)^(2/3)
Правила ввода функции, заданной в неявном виде
- Все переменные выражаются через x,y,z
- Примеры
≡ x^2/(z+y)
cos 2 (2x+zy) ≡ (cos(2*x+z*y))^2≡ z+(x-y)^(2/3)
Видео:11. Производная неявной функции примерыСкачать

Частные производные функции нескольких переменных
Пример 1 . z=2x 5 +3x 2 y+y 2 –4x+5y-1
Пример 2 . Найти частные производные 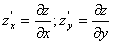
Находим частные производные:
Найдем частные производные в точке А(1;1)
Находим вторые частные производные:
Видео:Частные производные функции многих переменныхСкачать

Частные производные для функции от нескольких переменных
21 сентября 2015
Рассмотрим функцию от двух переменных:
[f=fleft( x,y right)]
Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:
функции $f$ в точке $M=left( <_>;<_> right)$ по переменной $x$ — это предел
Аналогично можно определить частную производную по переменной $y$ :
Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.
Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:
Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.
Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Что такое «частная производная»?
Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $yleft( x right)$ или $tleft( x right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.
Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.
Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.
Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $zleft( xy right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.
На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.
Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Задачи с радикалами и многочленами
Задача № 1
Чтобы не терять время зря, с самого начала начнем с серьезных примеров.
Для начала напомню такую формулу:
Это стандартное табличное значение, которое мы знаем из стандартного курса.
В этом случае производная $z$ считается следующим образом:
Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $frac$, то сначала мы воспользуемся стандартным табличным значением, а затем, поскольку под корнем стоит не $x$, а другое выражение, нам необходимо домножить нашу производную на еще одну из этого выражения по той же самой переменной. Давайте для начала посчитаем следующее:
Возвращаемся к нашему выражению и записываем:
В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:
Ответ найден. Теперь займемся $y$:
Задача № 2
Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.
Приступаем к делу:
Однако многим ученикам такая запись непонятна, поэтому запишем вот так:
Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.
Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:
Подставим полученные выражения в нашу формулу и получим:
По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:
За счет симметрии мы посчитали это выражение гораздо быстрее.
Нюансы решения
Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».
Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:
Далее мы точно таким же образом считаем еще две конструкции, а именно:
Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:
Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.
Видео:Математический анализ, 29 урок, Функции нескольких переменных. Частные производныеСкачать

Задачи с тригонометрическими функциями и логарифмами
Задача № 1
[zleft( x,y right)=sqrtcos frac]
Запишем следующие стандартные формулы:
Вооружившись этими знаниями, попробуем решить:
Отдельно выпишем одну переменную:
Возвращаемся к нашей конструкции:
Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:
Опять же посчитаем одно выражение:
Возвращаемся к исходному выражению и продолжаем решение:
Задача № 2
[zleft( x,y right)=ln left( x+ln y right)]
Запишем необходимую нам формулу:
Теперь посчитаем по $x$:
По $x$ найдено. Считаем по $y$:
Нюансы решения
Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.
Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.
Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $cos frac$ по $y$, то именно $y$ и является переменной, а $x$ везде остается константой. То же самое работает и наоборот. Ее можно выносить за знак производной, а производная от самой константы будет равна «нулю».
Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Задачи с показательными функциями и логарифмами
Задача № 1
Для начала запишем такую формулу:
Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:
Давайте решим отдельно следующее выражение:
Возвращаемся к нашей исходной конструкции и продолжаем решение:
Все, по $x$ посчитано.
Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:
В этом запишем так:
В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.
Теперь посчитаем по $y$:
Давайте решим одно выражение отдельно:
Продолжим решение нашей исходной конструкции:
Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.
Задача № 2
[zleft( x,y right)=xln left( <^>+y right)]
Давайте посчитаем одно выражение отдельно:
Продолжим решение исходной конструкции: $$
Вот такой ответ.
Осталось по аналогии найти по $y$:
Одно выражение посчитаем как всегда отдельно:
Продолжаем решение основной конструкции:
Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.
Нюансы решения
Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:
При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:
В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.
Видео:Математика без Ху!ни. Экстремум функции 2х переменных.Скачать

Задачи с тригонометрической функция и функцией с тремя переменными
Задача № 1
Давайте запишем такие формулы:
Давайте теперь решать наше выражение:
Отдельно посчитаем такую конструкцию:
Продолжаем решать исходное выражение:
Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:
Решим одно выражение отдельно:
Решаем до конца нашу конструкцию:
Задача № 2
На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.
Теперь разберемся с $y$:
Теперь остается найти по $z$:
Мы посчитали третью производную, на чем решение второй задачи полностью завершено.
Нюансы решения
Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.
В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.
Видео:6. Частные производные функции двух переменныхСкачать

Ключевые моменты
Окончательные выводы из сегодняшнего видеоурока следующие:
- Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
- При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.
Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!
Видео:Математика Без Ху!ни. Производная сложной функции.Скачать

Примеры решений задач: функции нескольких переменных
В этом разделе вы найдете готовые задания разного типа для функций нескольких переменных:
Видео:Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

Примеры: область определения ФНП
Задача 1. Найти область определения функции двух переменных $z=f(x,y)$. Изобразить ее на координатной плоскости и заштриховать.
Задача 2. Для данной функции найти область определения и изобразить ее на рисунке в системе координат.
Видео:ПРОИЗВОДНАЯ функции. Объяснение математического смысла.Скачать

Примеры: частные производные ФНП
Задача 3. Найти частные производные: $z=tg^3 (3x-4y)$
Задача 4. Найти частные производные второго порядка $z=sqrt$
Задача 5. Найти частные производные сложной функции:
$$ z=u^2 cdot ln v; quad u=frac, , v=x^2+y^2.$$
Задача 6. Проверить справедливость теоремы о смешанных производных второго порядка.
Задача 7. Найти полный дифференциал данной функции
Задача 8. Найти дифференциал второго порядка функции:
Задача 9. Для функции $z(x,y)$ двух переменных, неявно заданной уравнением $sin(xz)+cos(yz)=1$, найдите первый и второй дифференциалы в точке $x=y=1, z=0$.
Задача 10. Проверить, удовлетворяет ли функция двух переменных $z(x,y)$ указанному дифференциальному уравнению.
Видео:Полный дифференциалСкачать

Градиент, производная по направлению
Задача 11. Найти производную функции $f(x,y,z)$ в точке $M(x_0,y_0,z_0)$ по направлению вектора $overline$. Вычислить наибольшую скорость изменения функции в данной точке.
Задача 13. Найдите градиент, производную по направлению $overline$ и матрицу Гессе в точке $M$ заданной функции, где $u=f(x,y,z)=x^2z+z^2x^2+y^3$, $overline=$, $M(1,3,1)$.
Задача 14. Найти производную функции $u$ в точке $M$ по направлению нормали к поверхности $S$, образующей острый угол с положительным направлением оси $Oz$.
Видео:14. Производная сложной функции нескольких переменных Полная производная Примеры №1Скачать

Касательная плоскость и нормаль
Задача 15. Составить уравнения касательной плоскости и нормали к поверхности $x^2+y^2-x+2y+4z-13=0$ в точке $M(2,1,2)$.
Задача 16. Для кривой $overline=overline(t)$ найти в точке $t_0$ уравнение касательной, уравнение нормальной плоскости и вычислить кривизну линии.
$$ overline(t)=(t^2-3)overline + (t^3+2)overline+ln t overline, quad t_0=1 $$
Задача 17. Найти градиент, первый дифференциал, матрицу вторых производных, второй дифференциал функции $z=2xy-xy^4+5y^3-3$ в точке $A(2,-3)$. Составить уравнения касательной плоскости и соприкасающегося параболоида к графику данной функции.
Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Экстремумы функции нескольких переменных
Задача 18. Найти точки экстремума функции $z=x^2+xy+y^2+2x-y$.
Задача 19. Найти точки локального экстремума и экстремальные значения $z=x^2+y^2-xy+x+y$.
Задача 20. Исследовать на экстремум функцию $z=x^4+xy+fracy^2+5$.
Задача 21. Определите, при каких значениях параметра $a$ функция $z(x,y)=x^3+y^3+4xy-7x-7y+a(x-1)^2+a(y-1)^2$ в точке (1;1):
А) имеет максимум,
Б) имеет минимум,
В) не имеет экстремума.
Задача 22. Найдите (локальные) экстремумы функции трех переменных $f(x,y,z)=2x^2-xy+2xz-y+y^3+z^2$.
Видео:Математика это не ИсламСкачать

Приближенные вычисления
Задача 23. Вычислить приближенно значение функции $Z=Z(x,y)$ и данной точке с помощью дифференциала.
Задача 24. Дана функция $z=x^2+2xy+3y^2$ и две точки $А (2; 1)$ и $В (1,96; 1,04)$. Требуется:
1) вычислить точное значение функции в точке $В$;
2) вычислить приближённое значение функции в точке $В$, исходя из значения функции в точке $А$ и заменив приращение функции при переходе от точки $А$ к точке $B$ дифференциалом;
3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом.
Видео:18+ Математика без Ху!ни. Производная неявной функции.Скачать
Ряд Тэйлора
Задача 25. Разложите функцию $f(x,y)=x^2ln y + y^2$ по формуле Тейлора (с остаточным членом в форме Пеано) в окрестности точки $M(2;1)$ до членов второго порядка включительно. Выпишите первый и второй дифференциалы заданной функции.
Задача 26. Найти первые и вторые частные производные функции $F$ и записать формулу Тэйлора в указанной точке $x^0$.
Видео:Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать

Наибольшее и наименьшее значение в области
Задача 27. Найти наименьшее $m$ и наибольшее $M$ значения функции $z=f(x,y)=3-2x^2-xy-y^2$ в замкнутой области $D$, заданной системой неравенств $-1 le x le 1; 0le y le 2$. Сделать чертёж области $D$.
Задача 28. Экстремумы функций нескольких переменных. Требуется найти наибольшее и наименьшее значения функции $z=5x^2-3xy+y^2+4$ в области, ограниченной заданными линиями $x=0, y=0, x+y=2$.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение контрольной
Контрольное задание. Дана функция $f(x,y)=x^2+y^2-3xy$
1. Исследовать функцию $f$ на экстремум. Найти экстремальные значения функции.
2. Найти наибольшее и наименьшее значения функции $f$ в заданной области $D$.
3. Составить уравнение касательной плоскости к поверхности $z=f(x,y)$ в точке, где $x=x_0=1$, $y=y)0=3$.
4. Найти величину наибольшей скорости возрастания функции $f$ в точке $M_1(-1;1)$.
5. Вычислить производную функции $f$ в точке $M_1$ в направлении вектора $overline$. Каков характер изменения функции? Почему?
6. Найти угол между градиентами функции $f$ в точках $M_1$ и $M_2(2;2)$. Построить векторы и указать угол.
Видео:[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?Скачать
![[Calculus | глава 6] Неявное дифференцирование — что здесь происходит?](https://i.ytimg.com/vi/Vpa7bb6cg4I/0.jpg)
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.
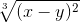 ≡ (x-y)^(2/3)
≡ (x-y)^(2/3)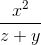 ≡ x^2/(z+y)
≡ x^2/(z+y) 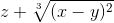 ≡ z+(x-y)^(2/3)
≡ z+(x-y)^(2/3)