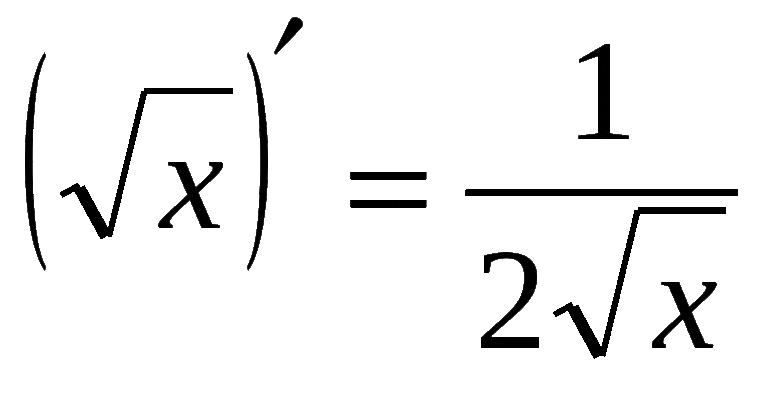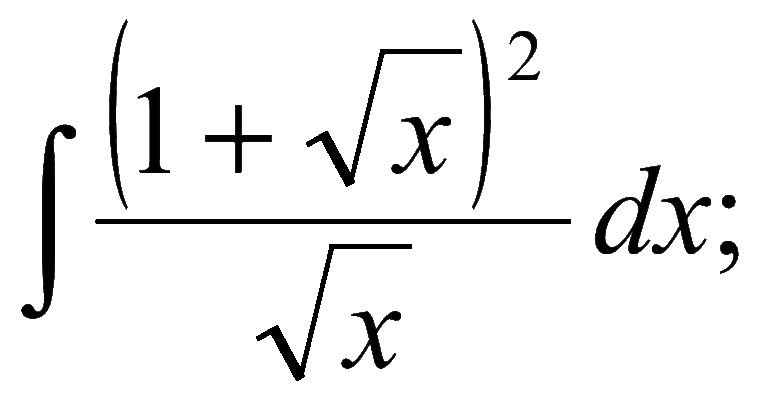Производная квадратного корня квадратного уравнения

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Производная корень из Х — формулы и примеры вычислений

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Понятие производной

Смысл производной основан на понятии предела функции. Состоит запись выражения из трёх частей, в одной из которых указывается, к чему стремится неизвестное. Оно может достигать как нуля, так и бесконечности. Таким образом, предел представляет собой динамическую величину. Например, пусть имеется некая функция f (x) = (1 + x) 1/x .

При иксе, который равен нулю, функция будет не определена, но можно исследовать, как она будет себя вести при приближении переменной к нулю. Для этого можно взять какое-либо значение икса и, подставив его в уравнение, вычислить функцию. Затем в формулу подставить иное произвольное число, но такое, чтобы оно было меньше предыдущего, то есть приближалось к нулю.

Выполнив несколько таких вычислений, можно увидеть, что значение функции начнёт приближаться к некой величине. Это значение и считается пределом рассматриваемого выражения при иксе, стремящемся к нулю.

Следует рассмотреть другую функцию: f (x) = 1 / x. Подставляя вместо икса различные числа, можно будет отметить, что при уменьшении исходной величины переменной числовое значение в ответе увеличивается, то есть результат функции ничем не ограничивается. Это означает, что при иксе, который стремится к нулю, предел будет равняться бесконечности.

Понятие предела помогает дать определение непрерывности. Функция f (x) непрерывна в точке x = c только тогда, когда знак предела и выражения можно поменять друг с другом местами: lim f (x) = f (lim x) = f с. Используя это свойство, можно определить точки разрыва и непрерывность. Зная определения можно понять, что представляет собой производная.

Пусть имеется линейная функция y = k * x + b, графиком которой будет прямая. При изменении икса на дельту по игреку будет происходить прирост на Δy = k * Δx. Получается, что величина k является скоростью роста функции: k = (f (x + Δx) — f (x)) / Δx. В этом случае график прямой имеет постоянный наклон, поэтому коэффициент k — константа.

Если же функция имеет произвольный вид, например, она состоит из сложного многочлена с дробями и квадратами, то, как вычислить постоянную k, непонятно. Вот тут на помощь и приходит понятие производной. Можно взять отношение дельта-икс на дельта-игрек и посмотреть, какой предел будет у функции: f'(x) = lim (f (x + Δx) — f (x)) / Δx. По сути, это действие и является нахождением производной.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Свойства корня

Находить производные подкоренных выражений невозможно без знания свойств степеней и корней. По определению, корнем квадратным из произвольного числа, которое больше нуля, называется такое неотрицательное число, которое при возведении в квадрат равняется этому числу.

То есть выражение √a = b тождественно равенству: b 2 = a. Например, √16 = 4, так как 4 2 = 16. Таким образом, можно утверждать, что корнем энной степени числа а будет такое выражение, которое при возведении в эту степень будет равняться а. Степень корня указывается в верхнем регистре значка, а основание записывается под знаком корня и называется подкоренным выражением.

Выделяют следующие свойства корней:

1. Если подкоренное выражение представляет умножение неотрицательных чисел, то корень квадратный будет равняться произведению корней членов выражения: √ a * b * … * n = √ a * √ b * … * √ n.
2. Когда под корнем находится отношение двух положительных чисел, то для решения выражения нужно извлечь корень из числителя и знаменателя, а после выполнить деление: √ a / b = √ a / b = √ a / √ b.
3. В случае когда а больше или равняется нулю и при этом n является натуральным, то корень из подкоренного выражения будет равняться а в степени n: √ a 2 n = a n .
4. При действительном числе и чётном значении показателей подкоренного выражения будет справедливым равенство: 2*m √ a 2*m = | a |. Если же показатель нечётный, то в ответе действительное число будет всегда положительное.
5. При извлечении корня из корня n √ m √ действие можно заменить произведением показателей при неизменном подкоренном выражении.
6. Сложение и вычитание корней возможно только в том случае, когда количественные или буквенные значения подкоренных выражений совпадают: n √ m + k √ m = (n + k) √ m.
7. Умножить корни с одинаковыми показателями возможно лишь тогда, когда показатель у всех перемножаемых членов одинаков: √ n * √ m = √ n * m.

Для любой степени существует основная формула, по которой может быть найдена производная.

Выглядит она как (x n )’ = n * x n -1 . Эта формула используется и для дифференцирования корней. Кроме этого, для успешного решения задач на нахождение производной квадратного корня из х необходимо знать и свойства степеней.

Видео:4. Вычисление производных примеры. Самое начало.Скачать

Нахождение выражения из Х

В общем случае формула производной корня из х равна дроби, в числителе которой стоит единица, а в знаменателе произведение степени корня на корень той же степени в подкоренном выражении, где находится неизвестное, уменьшенное на единицу, в степени. Математически это теорема записывается следующей формулой: ( n √x)’ = 1 / (n * n √ x n -1 ).

Эта формула имеет название первообразной. Она подходит для использования в выражениях любой кратности. В качестве примера можно рассмотреть взятие производной квадратного и кубического корня.

Так, для квадратного степенного уравнения справедливо выражение: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня х является дробью, делимое которой равняется единице, а делитель состоит из двойки, умножаемой на квадратный корень из неизвестного.

Аналогично можно сформулировать теорему и для нахождения производной кубического корня из x. Для этого случая решением задания на вычисление производной будет дробь, в числителе которой находится единица, а в знаменателе произведение тройки на корень кубический из икса в степени два. Формула для вычисления выглядит следующим образом: ( 3 √x)’ = 1 / (3 3 √x 2 ).

Можно обратить внимание, что, по сути, операция сводится к таким же действиям, как и при возведении дробей в степень, когда делитель равняется тому же показателю.

Иными словами, вычисление производной коренного выражения сводится к использованию формул для нахождения функции дроби.

Для доказательства формул используют следующие рассуждения. Производная переменной под квадратным корнем это то же, что и нахождение функции при возведении многочлена в степень одна вторая: (√x)’ = (х ½ )’. Поэтому можно воспользоваться формулой для расчёта производной неизвестного числа в степени эн. А значит, запись вида (х ½ )’ = ½ х -½ = 1 / (2√х) будет верной.

Формула производной третьей степени доказывается по такому же принципу. Используя правило дифференцирования и переписав кубический корень как тройную степень, можно записать: ( 3 √x)’ = (х 1/3 )’ = 1 / 3 * (x- 2/3 ) = 1 / 3 * ( 3 √х 2 ). Тут следует отметить, что степень -2/3 образовывается путём вычитания единицы из дроби, в числителе которой стоит два, а в знаменателе три.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Примеры заданий

При взятии производной функции f (x) = n √х m необходимо привести корень к степенному виду: f (x)’ = ( n √х m )’ = x m/n .

Так как из производных степени известно, что (x m )’ = m * x m-1 , то и алгоритм решения для нахождения ответа коренного выражения сводится к преобразованию исходного уравнения путём перехода к степени: f (x)’ = ( n √х m )’ = (x m/n )’ = m/n * x ( m/n) -1 = (m/n * n √х m-n ).

Этот подход позволяет не запоминать сложную формулу, что часто и используется на практике.

Для закрепления теории следует решить несколько типовых примеров:

1. Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x 2 )’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S ½ ) ‘ = (½) * S (½ — 1 ) * S’ = S -½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x 2 )’ = (3 — x 2 )’ / (2 * √ 3 — x 2 ) = — 2* x / 2 * √ 3 — x 2 = — x / √ 3 — x 2 .
2. Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
3. Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *(). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.

Видео:Комплексные корни квадратного уравненияСкачать

Расчёт на онлайн-калькуляторе

Попрактиковавшись в решении различных примеров, найти производную корня простых выражений будет довольно просто. Но если в заданиях будут стоять двойные корни или сама функция будет содержать большой многочлен, могут возникнуть проблемы. Связаны они обычно не с алгоритмом решения, а с трудностью вычисления и преобразования.

Такого рода задачи требуют повышенного внимания и скрупулёзности в расчётах. При этом поиску ответа понадобится уделить довольно много времени. Поэтому для помощи в нахождении производных коренных функций и существуют в интернете математические онлайн-калькуляторы.

Это сервисы, предлагающие бесплатно услуги по автоматическому расчёту производной любой сложности. Воспользоваться ими может каждый желающий, имеющий доступ к интернету. Для нахождения ответа не нужно обладать какими-то особыми знаниями. Всё что требуется от пользователя — ввести в предложенную форму условие и нажать кнопку «Вычислить». Весь процесс расчёта займёт одну-две секунды.

При этом большинство сервисов, кроме предоставления ответа на своих страницах, дает возможность ознакомиться с теоретическим материалом и предлагает рассмотреть решения заданий различной сложности. Поэтому вопроса, каким образом получился тот или иной ответ, возникнуть не должно.

Из различных онлайн-калькуляторов, считающих производные, можно выделить следующие:

1. Webmath.
2. Kontrolnaya-rabota
3. Onlinemschool.
4. Сalc.
5. Nauchniestati.

Сайты, используемые для вычислений, характеризуются интуитивно понятным интерфейсом, не содержащим нагромождения ненужной информации. На их страницах нет рекламного и вирусного кода.

Примечательно и то, что, выполнив пару вычислений, пользователь научится самостоятельно вычислять производную. А всё дело в том, что особенностью таких ресурсов является возможность обучения. Кроме непосредственно ответа, программа-расчётчик выдаст пошаговое вычисление с комментариями.

Кроме учащихся, онлайн-калькуляторы будут полезны и инженерам. Даже незначительная ошибка, допущенная в расчёте, приведёт к неверному ответу. В то же время при автоматических вычислениях появление ошибки исключено.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Производная квадратного корня квадратного уравнения

Производная от кубического корня из x равна единице, делённой на кубический корень из x в квадрате и делённому на три.

Пример производной функции, содержащей кубический корень с подробным решением:

Введём этот пример: cbrt(x^2-1)/x

Применим правило производной частного:

В силу правила, применим: получим

Затем примените цепочку правил. Умножим на :

Производная постоянной равна нулю.

В силу правила, применим: получим

В результате последовательности правил:

В силу правила, применим: получим

Теперь применим правило производной деления:

Тэги: производная

© Контрольная работа РУ — примеры решения задач

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Производная от корня квадратного х. Производная сложной функции. Примеры вычисления производных

Ниже приведены преобразования, поясняющие, почему формулы нахождения производной квадратного и кубического корня именно такие, как приведены на рисунке.

Разумеется, данные формулы можно вообще не запоминать, если принять во внимание, что извлечение корня производной степени — это то же самое, что возведение в степень дроби, знаменатель которой равен той же степени. Тогда нахождение производной корня сводится к применению формулы нахождения производной степени соответствующей дроби .

Видео:Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Производная переменной под квадратным корнем

Квадратный корень — это точно то же самое действие, что и возведение в степень 1/2, значит для нахождения производной корня можно применить формулу из правила нахождения производной от переменной в произвольной степени:

(х 1/2 )» = 1/2 х -1/2 = 1 / (2√х)

Видео:Квадратный корень. 8 класс.Скачать

Производная кубического корня (производная корня третьей степени)

Представим себе кубический корень как степень 1/3 и найдем производную по общим правилам дифференцирования. Краткую формулу можно посмотреть на картинке выше, а ниже расписано пояснение, почему именно так.

Степень -2/3 получается в следствие вычитания единицы из 1/3

Вывод формулы производной степенной функции (x в степени a). Рассмотрены производные от корней из x. Формула производной степенной функции высшего порядка. Примеры вычисления производных.

См. также: Степенная функция и корни, формулы и график
Графики степенной функции

Видео:8 класс, 25 урок, Формула корней квадратного уравненияСкачать

Основные формулы

Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .

Производная от корня степени n из x в степени m равна:
(2) .

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Теперь находим производную, применяя :
;
.
Здесь .

Формула (1) доказана.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.

Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .

Случай x 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции :

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом , , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Видео:Квадратное уравнение. 8 класс.Скачать

Примеры вычисления производных

Пример

Найдите производную функции:
.

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Операция отыскания производной называется дифференцированием.

В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).

Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.

Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.

Пример 1. Найти производную функции

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

Пример 2. Найти производную функции

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Видео:Извлечение квадратного корня из комплексного числа. 11 класс.Скачать

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200. ), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Видео:Производная сложной функцииСкачать

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.

Правило 2. Если функции

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной :

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

Правило 3. Если функции

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Где что искать на других страницах

При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций « .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.

А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).

Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.

По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.

Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».

Видео:5. Производная сложной функции примеры №1.Скачать

Пошаговые примеры — как найти производную

Пример 3. Найти производную функции

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

А проверить решение задачи на производную можно на .

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн .

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .

Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — (2 — 3) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .

Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.

Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Основные определения

Сложной функцией считается такая функция, у которой аргумент также является функцией.

Обозначается это таким образом: f (g (x)) . Имеем, что функция g (x) считается аргументом f (g (x)) .

Если есть функция f и является функцией котангенса, тогда g (x) = ln x – это функция натурального логарифма. Получаем, что сложная функция f (g (x)) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .

Очевидно, что g (x) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f (f 1 (f 2 (x))) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 (x) = 2 x + 1 x 3 — 5 — дробная рациональная функция.

Степень вложенности определено любым натуральным числом и записывается как y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

(f (g (x))) » = f » (g (x)) · g » (x)

Видео:Алгебра 8 класс : Формулы корней квадратного уравненияСкачать

Примеры

Найти производную сложной функции вида y = (2 x + 1) 2 .

По условию видно, что f является функцией возведения в квадрат, а g (x) = 2 x + 1 считается линейной функцией.

Применим формулу производной для сложной функции и запишем:

f » (g (x)) = ((g (x)) 2) » = 2 · (g (x)) 2 — 1 = 2 · g (x) = 2 · (2 x + 1) ; g » (x) = (2 x + 1) » = (2 x) » + 1 » = 2 · x » + 0 = 2 · 1 · x 1 — 1 = 2 ⇒ (f (g (x))) » = f » (g (x)) · g » (x) = 2 · (2 x + 1) · 2 = 8 x + 4

Необходимо найти производную с упрощенным исходным видом функции. Получаем:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Отсюда имеем, что

y » = (4 x 2 + 4 x + 1) » = (4 x 2) » + (4 x) » + 1 » = 4 · (x 2) » + 4 · (x) » + 0 = = 4 · 2 · x 2 — 1 + 4 · 1 · x 1 — 1 = 8 x + 4

При решении задач такого вида важно понимать, где будет располагаться функция вида f и g (x) .

Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .

Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g (x) – функцией синуса. Тогда получим, что

y » = (sin 2 x) » = 2 · sin 2 — 1 x · (sin x) » = 2 · sin x · cos x

Вторая запись показывает, что f является функцией синуса, а g (x) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как

y » = (sin x 2) » = cos (x 2) · (x 2) » = cos (x 2) · 2 · x 2 — 1 = 2 · x · cos (x 2)

Формула для производной y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) запишется как y » = f » (f 1 (f 2 (f 3 (. . . (f n (x)))))) · f 1 » (f 2 (f 3 (. . . (f n (x))))) · · f 2 » (f 3 (. . . (f n (x)))) · . . . · f n » (x)

Найти производную функции y = sin (ln 3 a r c t g (2 x)) .

Данный пример показывает сложность записи и определения расположения функций. Тогда y = f (f 1 (f 2 (f 3 (f 4 (x))))) обозначим, где f , f 1 , f 2 , f 3 , f 4 (x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.

Из формулы определения сложной функции имеем, что

y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x)

Получаем, что следует найти

1. f » (f 1 (f 2 (f 3 (f 4 (x))))) в качестве производной синуса по таблице производных, тогда f » (f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 a r c t g (2 x)) .
2. f 1 » (f 2 (f 3 (f 4 (x)))) в качестве производной степенной функции, тогда f 1 » (f 2 (f 3 (f 4 (x)))) = 3 · ln 3 — 1 a r c t g (2 x) = 3 · ln 2 a r c t g (2 x) .
3. f 2 » (f 3 (f 4 (x))) в качестве производной логарифмической, тогда f 2 » (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 » (f 4 (x)) в качестве производной арктангенса, тогда f 3 » (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2 .
5. При нахождении производной f 4 (x) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 » (x) = (2 x) » = 2 · x » = 2 · 1 · x 1 — 1 = 2 .

Производим объединение промежуточных результатов и получаем, что

y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x) = = cos (ln 3 a r c t g (2 x)) · 3 · ln 2 a r c t g (2 x) · 1 a r c t g (2 x) · 1 1 + 4 x 2 · 2 = = 6 · cos (ln 3 a r c t g (2 x)) · ln 2 a r c t g (2 x) a r c t g (2 x) · (1 + 4 x 2)

Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.

Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.

Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g (x) = t g x , f (g) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:

f » (g (x)) = (g 2 (x) + 3 g (x) + 1) » = (g 2 (x)) » + (3 g (x)) » + 1 » = = 2 · g 2 — 1 (x) + 3 · g » (x) + 0 = 2 g (x) + 3 · 1 · g 1 — 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g » (x) = (t g x) » = 1 cos 2 x ⇒ y » = (f (g (x))) » = f » (g (x)) · g » (x) = (2 t g x + 3) · 1 cos 2 x = 2 t g x + 3 cos 2 x

Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что

y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + (3 t g x) » + 1 » = = (t g x 2) » + 3 · (t g x) » + 0 = (t g x 2) » + 3 cos 2 x

Переходим к нахождению производной сложной функции (t g x 2) » :

f » (g (x)) = (t g (g (x))) » = 1 cos 2 g (x) = 1 cos 2 (x 2) g » (x) = (x 2) » = 2 · x 2 — 1 = 2 x ⇒ (t g x 2) » = f » (g (x)) · g » (x) = 2 x cos 2 (x 2)

Получаем, что y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.

Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1)

Данная функция может быть представлена в виде y = f (g (x)) , где значение f является функцией логарифма по основанию 3 , а g (x) считается суммой двух функций вида h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 и k (x) = ln 2 x · (x 2 + 1) . Очевидно, что y = f (h (x) + k (x)) .

Рассмотрим функцию h (x) . Это отношение l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 к m (x) = e x 2 + 3 3

Имеем, что l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) является суммой двух функций n (x) = x 2 + 7 и p (x) = 3 cos 3 (2 x + 1) , где p (x) = 3 · p 1 (p 2 (p 3 (x))) является сложной функцией с числовым коэффициентом 3 , а p 1 — функцией возведения в куб, p 2 функцией косинуса, p 3 (x) = 2 x + 1 — линейной функцией.

Получили, что m (x) = e x 2 + 3 3 = q (x) + r (x) является суммой двух функций q (x) = e x 2 и r (x) = 3 3 , где q (x) = q 1 (q 2 (x)) — сложная функция, q 1 — функция с экспонентой, q 2 (x) = x 2 — степенная функция.

Отсюда видно, что h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) + r (x)

При переходе к выражению вида k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) видно, что функция представлена в виде сложной s (x) = ln 2 x = s 1 (s 2 (x)) с целой рациональной t (x) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 (x) = ln x — логарифмической с основанием е.

Отсюда следует, что выражение примет вид k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x) .

Тогда получим, что

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1) = = f n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) · t (x)

По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Перед тем как находить производную корня, обратите внимание на остальные функции, присутствующие в решаемом примере. Если в задаче имеется много подкоренных выражений, то воспользуйтесь следующим правилом нахождения производной квадратного корня:

А для нахождения производной кубического корня примените формулу:

где через ³√х обозначен кубический корень из х.

Если , предназначенном для дифференцирования, встречается переменная в дробных , то переведите корня в степенную функцию с соответствующим показателем. Для квадратного корня это будет степень ½, а для кубического корня – ⅓:

где ^ обозначает возведение в степень.

Для нахождения производной степенной функции вообще и х^½, x^⅓, в частности, воспользуйтесь следующим правилом:

Для производной корня из этого соотношения вытекает:

Продифференцировав все , внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.

Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
производная константы (постоянного числа, C) равняется нулю: C» = 0;
постоянный множитель выносится за знак производной: (k*f)» = k * (f)» (f – произвольная функция) ;
производная суммы нескольких функций равняется сумме производных: (f + g)» = (f)» + (g)»;
производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)» = (f)»g + f (g)»;
производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)» = ((f)»g – f(g)») / g².

На этой странице вы сможете вычислять производную функции онлайн с получением подробного решения задачи. Решение производных функции производится с использованием тех правил дифференцирования, которые студенты изучают в курсе математического анализа в институте. Для того, чтобы найти производную функции нужно в поле «Функция» ввести функцию для дифференцирования согласно правил ввода данных.

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю: Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.

• производная корень из икс

📽️ Видео

Алгебра 8. Урок 5 - Квадратный корень и его свойстваСкачать