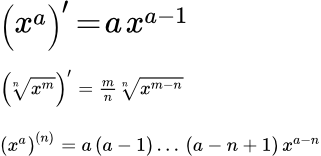Производная числа с уравнением в степени (2 видео)

Производная степенной функции (степени и корни)

Содержание

Основные формулы
Вывод формулы производной степенной функции
Случай x > 0
Вывод формулы производной от корня степени n из x в степени m
Случай x = 0
Случай x . При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби: , где m и n – целые числа, не имеющие общего делителя.
Производные высших порядков
Примеры вычисления производных
Пример
Еще примеры
Нахождение производной степенной функции
Формула производной степенной функции
Производная сложной степенной функции
Примеры задач
Производная показательной функции
Формула
Примеры вычисления производной показательной функции
📺 Видео

Видео:12. Производная степенно-показательной функцииСкачать

Основные формулы

Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .

Производная от корня степени n из x в степени m равна:
(2) .

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.

Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .

Случай x .
При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.

Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x . Например, при n = 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом, , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Видео:4.2 Производная Примеры для тренировкиСкачать

Примеры вычисления производных

Пример

Найдите производную функции:
.

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Еще примеры

Найти производные следующих функций, зависящих от переменной x :
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Автор: Олег Одинцов . Опубликовано: 09-04-2017

Видео:Найдите производную функции x^x ★ Как находить производные показательно-степенных функцийСкачать

Нахождение производной степенной функции

В данной публикации мы рассмотрим, чему равна производная степенной функций (в т.ч. сложной), а также разберем примеры решения задач для закрепления изложенного материала.

Видео:Математика Без Ху!ни. Производная сложной функции.Скачать

Формула производной степенной функции

Для функции f(x) = x n , где n – действительное число, справедливо следующее выражение:

Т.е. производная степенной функции равняется произведению показателя степени на основание в степени, уменьшенной на единицу.

n – может быть как положительным, так и отрицательным числом (в т.ч. дробным):

Производная сложной степенной функции

В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:

Видео:Производная логарифмической функции. 11 класс.Скачать

Примеры задач

Задание 1:
Вычислите производную функцию f(x) = x 3 /5 .

Решение:
Согласно правилам дифференцирования константу в виде дроби можно вынести за знак производной:

Применив формулу производной, рассмотренную выше, получаем:

Задание 2:
Найдите производную функции f(x) = x 2 + √ x – 6 .

Решение:
Первоначальный вид производной функции:
f ‘ (x) = (x 2 + √ x – 6) ‘.

С учетом правила дифференцирования суммы получаем:
f ‘ (x) = (x 2 ) ‘ + (√ x ) ‘ – (6) ‘.

Остается только вычислить производные по отдельности:

(x 2 ) ‘ = 2x 2-1 = 2x

(-6) ‘ = 0 (производная константы равна нулю)

Видео:Производная показательной функции. 11 класс.Скачать

Производная показательной функции

Видео:Вычисление производных. 10 класс.Скачать

Формула

Производная показательной функции равна произведению этой функции на натуральный логарифм основания степени.

Заметим, что если аргумент у показательной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$), то производную нужно находить по следующей формуле:

Видео:ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ решение производных функцийСкачать