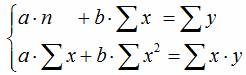Видео:9 класс, 7 урок, Уравнение прямойСкачать
Метод аналитического выравнивания
Назначение сервиса . Сервис позволит прямо на сайте в онлайн-режиме провести аналитическое выравнивание ряда yt, проверить наличие гетероскедастичности и автокорреляции остатков тестом Дарбина-Уотсона (см. пример аналитического выравнивания по прямой).
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Чтобы привести нелинейные зависимости к линейной используют метод выравнивания (линеаризацию).
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
В общем случае при аналитическом выравнивании используется метод наименьших квадратов:
- Система нормальных уравнений для линейной зависимости:
- Система нормальных уравнений для полинома второй степени (параболы):
- Система нормальных уравнений для полинома третьей степени:
Типичное задание. Произведите аналитическое выравнивание и выразите общую тенденцию развития розничного товарооборота торгового дома соответствующим аналитическим уравнением. Вычислите аналитические (выровненные) уровни ряда динамики и нанесите их на график вместе с фактическими данными.
Пример . По УР имеются данные о вводе в действие жилых домов и общежитий, тыс. м 2 . Для анализа динамики показателя ввода в действие жилых домов и общежитий вычислите:
- абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста. Полученные показатели представьте в виде таблицы;
- среднегодовые показатели — величину уровня ряда; абсолютный прирост темп роста и прироста. Сделайте выводы.
Постройте график динамики уровня ряда за период 1998 -2006 гг., проведите аналитическое выравнивание ряда (постройте математическую модель и график), сделайте прогноз на 2007 год.
Видео:11. Прямая в пространстве и ее уравненияСкачать
Аналитическое выравнивание ряда динамики.
Поможем написать любую работу на аналогичную тему
Наиболее точным и эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом фактические уровни ряда динамики заменяются теоретическими уровнями, вычисленными на основе определенной кривой, описываемой аналитическим выражением. Предполагается, что теоретическая кривая свободна от всевозможных колебаний и поэтому наиболее точно отображает общую тенденцию изменения во времени изучаемого показателя.
При аналитическом выравнивании ряда динамики, его уровни выражаются в виде функции времени.
(12.1)
где 
– теоретический уровень ряда динамики, вычисленный по определенному
аналитическом выражению на момент времени 
.
Чаще всего при аналитическом выравнивании используются следующие математические зависимости:
— линейная (уравнение прямой):
(12.2)
— параболическая (уравнение параболы):
(12.3)
— экспоненциальная (уравнение экспоненты):
(12.4)
— гиперболическая (уравнение гиперболы):
(12.5)
Выбор формы кривой во многом определяет результаты выявления тренда. Основанием для выбора формы кривой может использоваться содержательный анализ сущности развития данного явления. Можно опираться на результаты предыдущих исследований в данной области.
На практике для этих целей прибегают к анализу графического изображения уровней ряда динамики (линейной диаграммы). Однако из графического представления эмпирических данных не всегда удается произвести однозначный выбор формы кривой (вида уравнения). Поэтому целесообразно воспользоваться графическим изображением сглаженных уровней, в которых случайные и периодические колебания в некоторой степени оказываются сглаженными.
При выборе вида аналитической кривой для выравнивания ряда динамики можно воспользоваться следующими рекомендациями.
1. Линейная зависимость используется в том случае, когда в исходном ряде динамики наблюдается более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
2. Параболическая зависимость выбирается в тех случаях, когда абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных приростов (разности второго порядка) никакой тенденции развития не проявляют.
3. Экспоненциальные зависимости, если в исходном динамическом ряде наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии точного постоянства, – устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста).
Для решения уравнений аналитических кривых (формулы 12.2 – 12.5) в большинстве случаев используют метод наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выровненных (теоретических).
(12.6)
Рассмотрим технику аналитического выравнивания ряда динамики с использованием уравнения прямой, имеющей наиболее простое выражение, на следующем примере.
Пример. Имеются данные за последние 10 лет по заводу, где производятся запасные части для тракторов. Эти данные приведены в табл. 12.3.
1. Для того, чтобы выдвинуть гипотезу о предполагаемом законе распределения уровней ряда динамики, построим график зависимости выпуска продукции от времени. Такой график для нашего примера представлен на рис. 12.1.
Выпуск продукции на заводе (тыс. шт.)
Выпуск продукции, (
)
Видео:Аналитическое выравниваниеСкачать
Аналитическое выравнивания ряда динамики по прямой
2. Аналитическое выравнивания ряда динамики по прямой.
Рассмотрим применение метода на следующих данных о производстве продукции предприятием ОАО «Технополис»:
| Год | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Объем продукции, тыс. ед. | 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 | 18,0 |
Примем за точку отсчета 1995г. Тогда условные годы:
| Год | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| t. | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
Определим параметры уравнения прямой с использованием программы Excel:
| Годы | Объем продукции, тыс. ед. | Условные годы | yt | y1 | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1991 | 10 | -4 | 16 | -40 | 9,3 |
| 1992 | 10,7 | -3 | 9 | -32,1 | 10,41 |
| 1993 | 12 | -2 | 4 | -24 | 11,52 |
| 1994 | -10,3 | -1 | 1 | 10,3 | 12,63 |
| 1995 | 12,9 | 0 | 0 | 0 | 13,74 |
| 1996 | 16,3 | 1 | 1 | 16,3 | 14,85 |
| 1997 | 15,6 | 2 | 4 | 31,2 | 15,96 |
| 1998 | 17,8 | 3 | 9 | 53,4 | 17,07 |
| 1999 | 18 | 4 | 16 | 72 | 18,18 |
| Итого: | 123,6 | 0 | 60 | 66,5 | 123,66 |
Т.к. прямая имеет вид y1 = a0 + а1t , то
а0 = 123,6/9 = 13,74 тыс. ед.;
а1 = 66,5/ 60 = 1,11 тыс. ед;
уравнение прямой имеет вид:
Подставив в это уравнение значение t, получим выровненные теоретические значения.
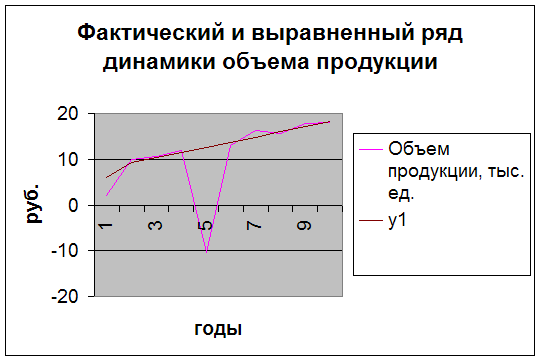
На рис. представлены графики фактических и теоретических уровней ряда.
Штриховая линия, построенная по значениям y1, показывает тенденцию роста объема производства на данном предприятии.
рис. Графики рядов динамики: 1 – фактического, 2 – выровненного.
🌟 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Лекция 23. Виды уравнений прямой на плоскости.Скачать
Практическое занятие Ряды динамикиСкачать
Уравнения прямой на плоскости | Векторная алгебраСкачать
Аналитическая геометрия, 6 урок, Уравнение прямойСкачать
Метод аналитического выравниванияСкачать
Введение в показатели рядов динамики Понятие динамического рядаСкачать
Уравнение прямой в пространстве. 11 класс.Скачать
Показатели рядов динамики ПримерСкачать
УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать
Метод скользящей среднейСкачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
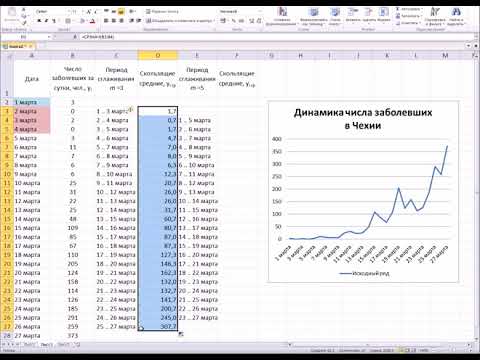
лекция по Статистике " Ряды динамики"Скачать
Общее уравнение динамики. Задача 1Скачать
Уравнение прямой на плоскостиСкачать
Основное уравнение динамики вращательного движения. 10 класс.Скачать
