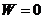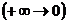Симуляция физики делает небольшие предсказания на основании законов физики. Эти предсказания на самом деле достаточно просты, что-то вроде «если объект вот здесь и он движется с такой скоростью в этом направлении, то за краткий промежуток времени он окажется вот тут». Мы создаём такие предсказания с помощью математической техники под названием интегрирование.
Темой этой статьи как раз и будет реализация такого интегрирования.
- Интегрирование уравнений движения
- Численное интегрирование
- Явный метод Эйлера
- Почему явный метод Эйлера не (всегда) так уж хорош
- Симплектический метод Эйлера
- Существует множество других методов интегрирования
- Реализация RK4
- Сравнение симплектического метода Эйлера и RK4
- Заключение
- Движение в центральном поле в физике
- Движение в центральном поле в физике
- Движение частицы в центральном поле
- 📺 Видео
Видео:Теоретическая механика. Лекция №5. Движение в центральном полеСкачать

Интегрирование уравнений движения
Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.
Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.
Ускорение — это темп изменения скорости от времени:
Аналогично, скорость — это темп изменения позиции от времени:
Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.
Видео:Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Движение в центральном полеСкачать

Численное интегрирование
Если вы не изучали дифференциальные уравнения в вузе, то можете вздохнуть спокойно — вы почти в такой же ситуации, что и те, кто их изучал, потому что мы не будем решать дифференциальные уравнения аналитически. Вместо этого мы будем искать решение численным интегрированием.
Вот как работает численное интегрирование: во-первых, начнём с исходной позиции и скорости, затем сделаем небольшой шаг вперёд, чтобы найти скорость и позицию в будущем. Затем повторим это, двигаясь вперёд небольшими шагами, используя результат предыдущих вычислений как исходную точку следующих.
Но как нам найти изменение скорости и позиции на каждом шаге?
Ответ лежит в уравнениях движения.
Давайте назовём наше текущее время t, а шаг времени dt или «delta time».
Теперь мы можем представить уравнения движения в понятном всем виде:
Интуитивно это понятно: если вы находитесь в автомобиле, движущемся со скоростью 60 км/ч, то за один час вы проедете 60 км. Аналогично, автомобиль, ускоряющийся на 10 км/ч в секунду, через 10 секунд будет двигаться на 100 км/ч быстрее.
Разумеется, эта логика сохраняется, только когда ускорение и скорость постоянны. Но даже если они меняются, то это для начала вполне неплохая аппроксимация.
Давайте представим это в коде. Начнём с стационарного объекта массой один килограмм и приложим к нему постоянную силу в 10 кН (килоньютонов) и сделаем шаг вперёд, принимая, что один временной шаг равен одной секунде:
Вот каким будет результат:
Как вы видите, на каждом шаге мы знаем и позицию, и скорость объекта. Это и есть численное интегрирование.
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Явный метод Эйлера
Вид интегрирования, который мы только что использовали, называется явным методом Эйлера.
Он назван в честь швейцарского математика Леонарда Эйлера, впервые открывшего эту технику.
Интегрирование Эйлера — это простейшая техника численного интегрирования. Она точна на 100% только когда темп изменений в течение шага времени постоянен.
Поскольку в примере выше ускорение постоянно, интегрирование скорости выполняется без ошибок. Однако мы ещё интегрируем и скорость для получения позиции, а скорость увеличивается из-за ускорения. Это значит, что в проинтегрированной позиции возникает ошибка.
Но насколько велика эта ошибка? Давайте выясним!
Существует аналитическое решение движения объекта при постоянном ускорении. Мы можем использовать его, чтобы сравнить численно интегрированную позицию с точным результатом:
Через 10 секунд объект должен был переместиться на 500 метров, но явным метод Эйлера даёт нам результат 450. То есть погрешность в целых 50 метров всего за 10 секунд!
Кажется, что это невероятно плохо, но в играх обычно для шага физики берётся не такой большой временной интервал. На самом деле, физика обычно вычисляется с частотой, примерно равной частоте кадров дисплея.
Если задать шаг dt = 1 ⁄100, то мы получим гораздо лучший результат:
Как вы видите, это достаточно хороший результат, определённо вполне достаточный для игры.
Видео:Механика - Движение в поле центральных сил. Момент импульсаСкачать

Почему явный метод Эйлера не (всегда) так уж хорош
С достаточно малым шагом времени явный метод Эйлера при постоянном ускорении даёт вполне достойные результаты, но что будет, если ускорение не постоянно?
Хорошим примером переменного ускорения является система пружинного амортизатора.
В этой системе масса присоединена к пружине, и её движение гасится чем-то вроде трения. Существует сила, пропорциональная расстоянию до объекта, которая притягивает его к исходной точке, и сила, пропорциональная скорости объекта, но направленная в противоположном направлении, которая замедляет его.
Здесь ускорение в течение шага времени совершенно точно изменяется, но эта постоянно меняющаяся функция является сочетанием позиции и скорости, которые сами постоянно изменяются за шаг времени.
Вот пример гармонического осциллятора с затуханием. Это хорошо изученная задача, и для него существует аналитическое решение, которое можно использовать для проверки результата численного интегрирования.
Давайте начнём со слабозатухающей системы, в которой масса колеблется рядом с исходной точкой, постепенно замедляясь.
Вот входные параметры системы масса-пружина:
- Масса: 1 килограмм
- Исходная позиция: 1000 метров от исходной точки
- Коэффициент упругости по закону Гука: k = 15
- Коэффициент затухания по закону Гука: b = 0.1
И вот график точного решения:
Если для интегрирования этой системы мы применим явный метод Эйлера, то получим следующий результа, который я отмасштабировал по вертикали:
Вместо затухания и сближения с исходной точкой, система со временем набирает энергию!
При интегрировании явным методом Эйлера и с dt= 1 ⁄100 такая система нестабильна.
К сожалению, поскольку мы уже интегрируем с малым шагом времени, то не имеем практичных способов повышения точности. Даже если мы уменьшим шаг времени, то всегда будет коэффициент упругости k, при котором мы получим такое поведение.
Видео:Аналитическая механика 5. Движение точки в центральном поле.Скачать

Симплектический метод Эйлера
Мы можем рассмотреть ещё один интегратор — симплектический метод Эйлера.
В большинстве коммерческих игровых физических движков используется этот интегратор.
Переход от явного к симплектическому методу Эйлера заключается только в замене:
Использование симплектического интегратора Эйлера при dt = 1 ⁄100 для системы пружинного амортизатора даёт стабильный результат, очень близкий к точному решению:
Даже несмотря на то, что симплектический метод Эйлера имеет ту же степень точности, что и явный метод (степень 1), при интегрировании уравнений движения мы получаем намного лучший результат, потому что оно является симплектическим.
Видео:Кеплерова задача. Часть 1. Уравнение траекторииСкачать

Существует множество других методов интегрирования
И теперь нечто совершенно другое.
Неявный метод Эйлера — это способ интегрирования, хорошо подходящий для интегрирования жёстких уравнений, которые при других методах становятся нестабильными. Его недостаток заключается в том, что он требует решения системы уравнений на каждом шаге времени.
Интегрирование Верле обеспечивает бо́льшую точность, чем неявный метод Эйлера, и требует меньше памяти при симуляции большого числа частиц. Это интегратор второй степени, который тоже является симплектическим.
Существует целое семейство интеграторов, называемое методами Рунге-Кутты. На самом деле, явный метод Эйлера считается частью этого семейства, но в него входят интеграторы и более высокого порядка, самым классическим из которых является метод Рунге-Кутты порядка 4 (Runge Kutta order 4) или просто RK4.
Это семейство интеграторов названо в честь открывших их немецких физиков: Карла Рунге и Мартина Кутты.
RK4 — это интегратор четвёртого порядка, то есть накапливаемая ошибка имеет порядок четвёртой производной. Это делает метод очень точным, гораздо более точным, чем явный и неявный методы Эйлера, имеющие только первый порядок.
Но хотя он более точен, нельзя сказать, что RK4 автоматически становится «лучшим» интегратором, или даже что он лучше симплектического метода Эйлера. Всё гораздо сложнее. Тем не менее, это довольно интересный интегратор и его стоит изучить.
Видео:Задача: из лагранжиана в гамильтониан.Интегрирование уравнений движения.Случай одной степени свободыСкачать

Реализация RK4
Существует уже много объяснений математики, используемой в RK4. Например: здесь, здесь и здесь. Я настоятельно рекомендую изучить его выведение и понять, как и почему он работает на математическом уровне. Но я понимаю, что целевая аудитория этой статьи — программисты, а не математики, поэтому мы здесь будем рассматривать только реализацию. Так что давайте приступим.
Прежде чем приступить, давайте зададим состояние объекта как struct в C++, чтобы можно было удобно хранить позицию и скорость в одном месте:
Также нам нужна структура для хранения производных значений состояний:
Теперь нам нужна функция для вычисления состояния физики из t в t+dt с помощью одного набора производных, а после этого для вычисления производных в новом состоянии:
Функция ускорения управляет всей симуляцией. Давайте используем её в системе пружинного амортизатора и вернём ускорение для единичной массы:
То, что нужно здесь записать, разумеется, зависит от симуляции, но необходимо структурировать симуляцию таким образом, чтобы можно было вычислять ускорение внутри этого метода для заданных состояния и времени, в противном случае он не подойдёт для интегратора RK4.
Наконец, мы получаем саму процедуру интегрирования:
Интегратор RK4 делает выборку производной в четырёх точках, чтобы определить кривизну. Заметьте, как производная a используется при вычислении b, b используется при вычислении c, и c для d. Эта передача текущей производной в вычисление следующей и даёт интегратору RK4 его точность.
Важно то, что каждая из этих производных a, b, c и d будет разной, когда темп изменения в этих величинах является функцией времени или функцией самого состояния. Например, в нашей системе пружинного амортизатора ускорение является функцией текущей позиции и скорости, которые меняются в шаге времени.
После вычисления четырёх производных наилучшая общая производная вычисляется как взвешенная сумма, полученная из разложения в ряд Тейлора. Эта комбинированная производная используется для перемещения позиции и скорости вперёд во времени, точно так же, как мы делали это в явном интеграторе Эйлера.
Видео:Уравнение движенияСкачать

Сравнение симплектического метода Эйлера и RK4
Давайте подвергнем проверке интегратор RK4.
Очевидно, что поскольку он является интегратором более высокого порядка (четвёртый против первого) он наглядно будет более точен, чем симплектический метод Эйлера, правда?
Неправда. Оба интегратора так близки к точному результату, что при таком масштабе почти невозможно найти между ними разницу. Оба интегратора стабильны и очень хорошо повторяют точное решение при dt= 1 ⁄100.
При увеличении видно, что RK4 действительно более точен, чем симплектический метод Эйлера, но стоит ли эта точность сложности и лишнего времени выполнения RK4? Трудно судить.
Давайте постараемся и посмотрим, сможем ли мы найти значительное различие между двумя интеграторами. К сожалению, мы не сможем долго наблюдать за этой системой, потому что она быстро затухает до нуля, поэтому давайте перейдём к простому гармоническому осциллятору, который колеблется бесконечно и без затуханий.
Вот точный результат, к которому мы будем стремиться:
Чтобы усложнить интеграторам задачу, давайте увеличим шаг времени до 0,1 секунды.
Теперь запустим интеграторы на 90 секунд и увеличим масштаб:
Через 90 секунд симплектический метод Эйлера (оранжевая кривая) сдвинулся по фазе относительно точного решения, потому что его частота немного отличалась, в то время как зелёная кривая RK4 соответствует частоте, но теряет энергию!
Мы чётко можем это заметить, увеличив шаг времени до 0,25 секунды.
RK4 сохраняет верную частоту, но теряет энергию:
А симплектический метод Эйлера в среднем намного лучше сохраняет энергию:
Но от сдвигается от фазы. Какой интересный результат! Как вы видите, если RK4 имеет более высокий порядок точности, то он не обязательно «лучше». В этом вопросе есть множество нюансов.
Видео:ЧК МИФ 1 2 03 07 L3 Численное интегрирование уравнений движенияСкачать

Заключение
Мы реализовали три различных интегратора и сравнили результаты.
- Явный метод Эйлера
- Симплектический метод Эйлера
- Метод Рунге-Кутты порядка 4 (RK4)
Так какой же интегратор стоит использовать в игре?
Я рекомендую симплектический метод Эйлера. Он «дёшев» и прост в реализации, гораздо стабильнее явного метода Эйлера и в среднем стремится к сохранению энергии даже при близких к предельным условиях.
Если вам действительно нужна бОльшая точность, чем у симплектического метода Эйлера, я рекомендую посмотреть на симплектические интеграторы более высокого порядка, рассчитанные на гамильтоновы системы. Таким образом вы изучите более современные техники интегрирования высокого порядка, которые лучше подходят для симуляций, чем RK4.
И наконец, если вы всё ещё пишете в игре такое:
То потратьте секунду и замените эти строки на:
Видео:Законы КеплераСкачать

Движение в центральном поле в физике







Видео:Лекция №5 "Момент импульса в квантовой механике. Движение в центральном поле"Скачать

Движение в центральном поле в физике
- Перемещение центра поля Проблема движения двух объектов была сведена к проблеме движения одного объекта, что привело к проблеме определения движения частицы во внешнем поле, где существует потенциальная энергия.
Зависит только от определенного фиксированного расстояния r Точка; такое поле называется центральным. прочность F _ DU (G) _ DU R доктор др г Действуя на частицы, абсолютное значение Это также только от r и направлено на каждую точку вдоль радиус-вектора. При перемещении в центр, как уже указано в §9 Поле содержит момент системы относительно центра поля.
траектория частицы в центральном поле полностью находится в одной плоскости Людмила Фирмаль
Для одной частицы это М = [г]. Поскольку векторы M и r перпендикулярны друг другу, инвариантность m означает, что радиус-вектор всегда остается в одной плоскости (плоскости, перпендикулярной M) при движении частицы. Следовательно, .
Введите полярные координаты r и cp и запишите функцию Лагранжа в следующем формате (ср. (4.5)) L = ^ (r2 + r2cp2) -C / (r). (14.1) Эта функция явно не включает координаты cf. Обобщенные координаты, явно не включенные в Лагранжева функция называется патруль. Благодаря уравнению Лагранжа вы можете сделать следующее для этих координат: d d _ dL _ q dt dqi dqi ’ Таким образом, соответствующий обобщенный импульс p1 = db / dcc является интегралом движения.
- Эта ситуация значительно упрощает задачу интегрирования уравнений движения при наличии периодических координат. В этом случае обобщенный импульс = tg2f Соответствует моменту Mz = M (см. (9.6)), поэтому вернемся к известному закону сохранения момента M = gag2p = const. (14-2) Для плоского движения одной частицы в центре Районы, разрешенные этим законом Геометрическая интерпретация.
Формула (l / 2) r * rdcp представляет площадь сформированного сектора Два почти бесконечных радиуса вектора и элементы орбитальной дуги (рисунок 8). С этим? И мы пишем момент частицы на форме М = 2 т /, (14,3) Здесь производная / называется скоростью сектора.
сохранение импульса означает постоянство скорости сектора Людмила Фирмаль
по Напротив, — за тот же период радиус-вектор движущейся точки описывает равную площадь (так называемый Второй закон Кеплера) Полное решение проблемы движения центральной частицы Проще всего получить поле по закону сохранения энергии и импульса, не выписывая само уравнение движения.
Из (14.2), выражая φ через M и подставляя энергию в уравнение, E = (f2 + rV) + и (r) = ^ + J ^ + и (r). (14.4) Отсюда r = ± = J ^ [E-U (r) — ^ (14,5) дт в т т2г2 Или разделить и объединить переменные = [dr = + const. (14,6) J / 2, YYY 77, W м — [E-U (r)] Кроме того, напишите (14.2) в форме dip = -m ^ r2z dti Подставляя dt из (14.5) здесь, φ = [(М / г) др конст. (14-7) J y / 2t [E-U (g)] -M 2 / r2 V ‘ Уравнения (14.6) и (14.7) решают общую сформулированную задачу.
Второй из них определяет отношения между гифами. Орбитальное уравнение. Уравнение (14.6) неявно определяет расстояние r движущейся точки от центра как функцию Время. Обратите внимание, что угол φ всегда изменяется монотонно со временем — (14.2) показывает, что φ не меняет знак. Уравнение (14.4) показывает, что радиальная часть движется Его можно рассматривать как одномерное движение в поле с «эффективной» потенциальной энергией.
= Гг) + (14,8) Значение M2 / (2tr2) называется центробежной энергией. значение г Италбо йцинарг тюялеропо + & * = E ′ Перемещение расстояния от центра. Если выполнено уравнение (14.9), лучевая скорость r Она исчезнет. Это не означает остановку частиц Поскольку угловая скорость φ не исчезает, это истинное одномерное движение). Уравнение r = 0 означает «точку поворота» орбиты, где функция r (t) возрастает с ростом.
Уменьшить или наоборот. Если допустимая область изменения r ограничена только одним условием r ^ rmin, движение частицы бесконечно Траектория исходит из бесконечности и уходит к дьяволу Руки и ноги. Если есть две границы rmin и rmax в области флуктуаций r, Движение конечно и траектория полностью лежит В кольце, окруженном кружками r = rmax и r = = ^ min-
Однако это не означает, что траектория действительно является замкнутой кривой. р от При переходе от rmax к rmin, а затем к rmax радиус-вектор поворачивается на равный угол Df в соответствии с (14.7). Макс Der = 2 f, (M / r2) dr (14.10) J d / 2t (E-U) -M2 / g2 V 7 T минут Состояние закрытия орбиты Этот угол равен рациональному числу 2тг, т.е. была форма Df = 2 м / n, где w, n- Целое число Тогда н
Повторите этот период Завершить радиус-вектор момента времени, около t Компания соответствует ему Начальная стоимость То есть путь закрыт. Однако это исключение и для любой формы U (r) угол Не разумно Часть 2тг. Поэтому в общем случае орбита фи Движение пряжи не закрыто.
Она проходит минимальные и максимальные расстояния много раз Все кольцо между двумя граничными кругами заполняется за бесконечное время (например, как на рисунке 9). Есть только два типа в центральном поле. Все компактно поддерживаемые траектории замкнуты. Это поля, в которых потенциальная энергия частиц пропорциональна г Или г2.
Первый из этих случаев будет обсуждаться в следующем разделе, а второй случай соответствует так называемому пространственному осциллятору (см. Вопрос 3, §23). В точке поворота квадратный корень (14,5) (и И подынтегральные выражения (14.6) и (14.7) меняют знак.
Считая угол cp от направления вектора радиуса, нарисованного в точке поворота, отрезок траектории, примыкающий к этой точке с обеих сторон, отличается только знаком cp для всех одинаковых значений r.
Это означает, что траектория симметрична относительно указанного направления. введение Пройдите отрезок от одной из точек r = rmax локус к точке r = rmin, то есть симметрия Тот же сегмент до следующей точки Повторяя один и тот же отрезок в прямом и обратном направлениях, например, r = rmax, получается вся траектория.
Это Относится к двум бесконечным трекам Симметричная ветвь, отходящая от точки поворота Реклама бесконечна. Наличие центробежной энергии (при переходе от М ф 0), r- »0 до бесконечности, как smallfraclr2 Обычно перемещение делает вторжение невозможным Последние частицы в центре поля, даже если они сами обладают привлекательными свойствами.
«Падение» частиц в центр возможно только в том случае, если потенциальная энергия имеет тенденцию быть достаточно быстрой. k — для m — y0. Из неравенства V ^ — = E-U (r) -> 0 2 v ‘2mr2 или r2U (r) + Другими словами, U (r) должен стремиться -о либо-> ca> либо g2 2t Пропорционально —n> 2. Задание 1. Интегрировать уравнение движения шарикового маятника. Точка массы w движется вдоль поверхности сферы радиуса I Гравитационное поле.
Решения. Сферические координаты, начиная с центра сферы, Если полярная ось направлена вертикально вниз, функция Лагранжа Ник Координаты (р периодическая, поэтому обобщенный импульс сохраняется Rf, который соответствует мгновенному компоненту z: Интеграции (3) и (4) сводятся к эллиптическим интегралам соответственно. Но первый и третий вид.
Область движения вдоль угла 0 определяется условием E> Ј / eff и его гра. по ница-уравнению E = TJ3f. Последний куб Уравнение cos0 имеет два корня в интервале от -1 до +1, определенно Положение двух параллельных кругов на сфере, Вся траектория теперь закончилась. 2. Интегрировать уравнение движения массы Ожог вдоль поверхности конуса (угол 2а на вершине) Вертикально, сверху вниз, в гравитационном поле. Решения.
Функция Лагранжа L = t2 (02 + sin2 0 • ф2) + mgl cos 0. ml2 sin2 0 • ф = Mz = const. (I) Энергия-мгл cos0. (2) Определите 0 отсюда и отделите и получите переменную (3) Где вводится «эффективная потенциальная энергия» Интегралы (3) и (4) сводятся к эллиптическим интегралам типа 1 и типа 3 соответственно.
Область движения вдоль угла 0 определяется условием E> Ј / eff, а ее граница определяется уравнением E = TJ3ph. Последний куб Уравнение cos0. С двумя маршрутами, определяющими расположение двух параллельных окружностей на сфере, с интервалом от -1 до +1 Вся траектория теперь закончилась.
2. Интегрирует уравнение движения материальной точки, движущейся вдоль поверхности размещенного конуса (угол 2а у вершины) Вертикально, сверху вниз, в гравитационном поле. Решения. Функция Лагранжа Аналогично вопросу 1, PhD т = / ^ [E-eef (г)] Mz F Dr Фsin2 al / 2m: J / r2 JE-U3ф (r) ‘ + мср cos a- ML 2mr2 sin2 oc Условие E = ief (g) является кубическим уравнением для g (в случае Mz 0 0) и имеет два положительных корня.
Определите положение двух горизонтальных кругов на поверхности конуса. Траектория теперь закончена. 3. Объедините уравнение движения плоского маятника с точкой подвеса (с массой w ), которая может двигаться горизонтально (см. Рисунок 2). Решения. В функции Лагранжа в задаче 2 из § 5 координата x является периодической.
Следовательно, обобщенный импульс Px, который соответствует горизонтальной составляющей полного импульса системы, сохраняется. Px = (m i + GP2) x + 777-2 / f COS f = C Onst (1) Вы можете просмотреть всю систему в любое время. Тогда const = 0 и Интеграл уравнения (1) дает соотношение (T 1 + m2) х + m21 sinф = const, (2) Указывает, что центр инерции системы не перемещается горизонтально.
Используйте (1), чтобы получить энергию в следующем формате: ITI2I2 dcp. 11 (7771 + 7772) J VÅ + 7772 г / COSф 2 Координата X2 = x + lsin (p, 2/2 = lcos ((2) представляет p частицы m2, используя φ, траектория этой частицы — горизонтальная ось / 7771 / (7771 + m2) и вершина Вы можете видеть, что это эллиптический сегмент с I. I. 777-> oo, чтобы вернуться к нормальной математике Маятник, который рисует дугу круга.
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Форш П. А. - Теоретическая механика - Интегрирование уравнений движения. Одномерное движениеСкачать

Движение частицы в центральном поле
12.1. Сохранение момента импульса в центральном поле.
Сила называется центральной, если для всех точек поля она направлена к одной и той же точке (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил, или силовым центром.
Уже из определения следует, что центральные силы консервативны.
Итак, центральная сила:
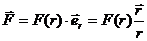
Поскольку эта сила консервативна, то можно ввести потенциальную энергию:
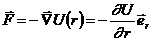
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:
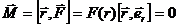
Тогда из уравнения моментов (11.5) получаем, что момент импульса есть постоянная величина.
При движении частицы в центральном поле полный момент импульса сохраняется, несмотря на то, что система (одна частица) не является замкнутой.

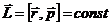
Так как 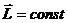
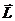
перпендикулярен к векторам 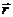
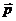
происходит в плоскости, перпендикулярной к 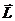
что частица в поле центральных сил движется по плоской орбите.
Если ось 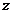
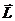
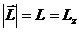
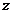
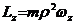
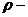
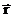
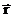
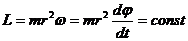
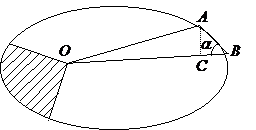 |
Пусть частица движется в в поле центральных сил по плоской траектории, представляющей собой замкнутую кривую.
Площадь 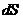
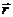
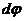
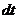
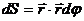
Выберем за начало отсчета точку О и найдем площадь сектора 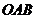
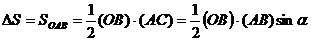
Здесь 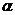
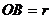
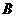
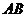
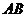
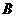
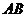
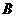
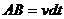
Тогда можем записать
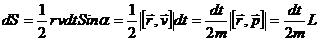
Вводя понятие секториальной скорости как площади, описываемой радиусом-вектором 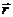
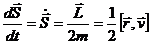
Т.о., мы получили математическое выражение 2-го закона Кеплера, устанавливающего постоянство секториальной скорости планеты 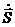
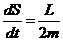
Этому закону подчиняется, например, движение планет по эллиптическим орбитам.
Примечание: Закон сохранения момента импульса частицы, движущейся в центральном поле иногда
называют “интегралом площадей”.
Итак, свойства движения частицы в центральном поле:
1) движение плоское, плоскость проходит через точку 0, определенный относительно которой момент импульса частицы сохраняется.
2) секториальная скорость постоянна (II закон Кеплера).
12.2. Закон сохранения энергии в центральном поле.
Центральные силы консервативны, следовательно, полная энергия частицы в системе «силовой центр – частица» (замкнутая система) сохраняется.
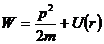
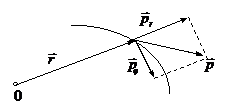
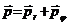
В полярных координатах выражения для момента импульса 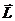
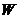
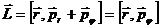
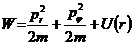
В выражении (12.10) 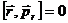
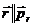
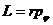
т.к. траектория частицы плоская и 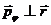
Если, воспользовавшись (12.10), исключить из уравнения (12.11) азимутальную составляющую импульса частицы 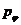
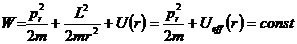
Примечание. Величину 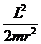
Уравнение (12.12) содержит только одну неизвестную – радиальную компоненту импульса 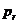
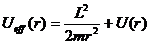
Т.о., можно сказать, что задача о движении частицы в центральном поле сводится к нахождению условий финитности (инфинитности) одномерного движения частицы в радиальном направлении в поле, описываемом эффективной потенциальной функцией 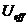
12.3. О траектории движения частицы.
Представим компоненты импульса, записанного в полярных координатах, следующим образом:
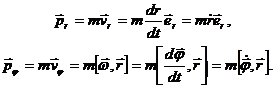
Далее, т.к. угол между вектором угловой скорости 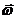
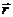
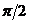
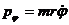
Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем
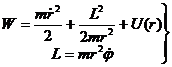
Из второго уравнения (12.15) получаем
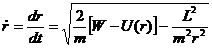
Разделяя переменные, находим в неявном виде зависимость 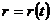
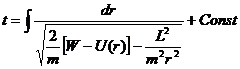
Из первого уравнения (12.15) имеем
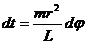
Исключив из уравнений (12.15) время 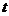
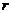
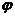
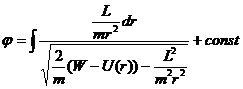
Значения 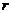
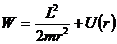
определяют границы области движения по расстоянию от центра поля. При выполнении равенства (12.18) радиальная скорость 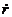
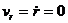
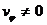
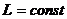
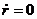
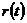
Если область допустимого изменения 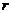
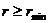
Если область изменения 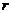
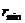
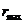
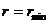
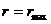
За время прохождения одной петли (от 
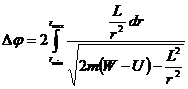
Условие замкнутости траектории: траектория будет замкнутой, если 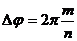
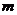
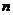
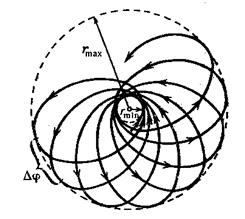
на угол, равный рациональной части от 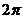
Тогда через 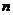
вектор точки, сделав 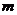
первоначальным значением, т.е. траектория замкнется.
Однако такой исход является скорее исключением,
нежели правилом. Существуют лишь два типа центральных
полей, в которых все траектории финитных движений
замкнуты. Это поля, где зависимость потенциальной энергии
от расстояния от центра поля имеет вид:
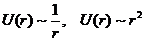
Задача Кеплера (Кеплерова задача) — задача о движении частицы в поле центральных сил, убывающих обратно пропорционально квадрату расстояния от центра поля. Этому закону подчиняются силы гравитационного притяжения между точечными массами (или телами, обладающими сферической симметрией), а также кулоновские силы, действующие между точечными электрическими зарядами. Поэтому такие поля являются важнейшим случаем центральных полей.
В таком поле потенциальная энергия частицы определяется выражением
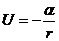
где 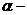
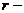
Рассмотрим случай, когда 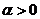

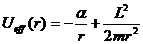
от расстояния от центра поля показана на рисунке.
При 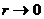
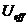
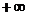
она стремится к нулю со стороны отрицательных
значений; при 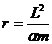
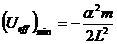
Из рисунка видно, что движение частицы будет инфинитным при 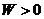
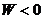
Форму траектории получаем интегрированием формулы (12.15) после подстановки 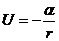
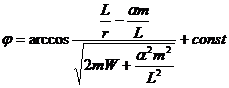
Выбирая начало отсчета угла 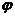
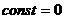
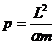
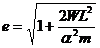
получим уравнение траектории в виде:
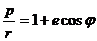
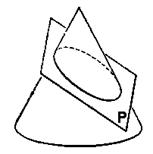
Приложение. Выражение (13.6) – уравнение конического сечения с фокусом в начале координат в полярных координатах; 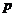
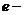
Коническими сечениями называют эллипс, параболу и гиперболу, т.к. их можно получить на поверхности
круглого конуса в пересечении с плоскостью 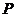
вершину конуса. При этом поверхность конуса предполагается
неограниченно продолженной в обе стороны от вершины.
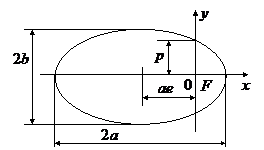
Если плоскость 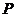
коническое сечение есть эллипс. Эллипсом называется геометрическое
место точек, сумма расстояний от которых до двух данных точек,
называемых его фокусами, есть величина постоянная. Отношение
фокусного расстояния эллипса к длине его большой оси называется
эксцентриситетом эллипса 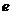
Если плоскость 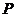
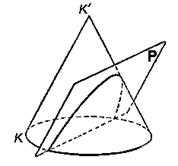
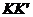
называют геометрическое место точек, равноотстоящих
от данной точки, называемой фокусом, и данной прямой
называемой директрисой. Исходя из её определения,
эксцентриситет параболы принимают равным единице
( 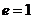
Если плоскость 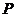
( 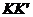
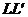
Гиперболой называется геометрическое место точек, разность
расстояний от которых до двух данных точек, называемых
фокусами, есть величина постоянная. Величина, определяемая
как отношение фокусного расстояния к длине действительной
оси (длина отрезка, соединяющего вершины гиперболы), называется
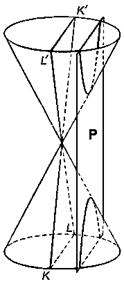
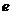
Из аналитической геометрии известно, что все эллипсы (кроме
окружности), параболы и гиперболы обладают следующим свойством: для
каждой из этих линий остается неизменным отношение
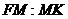
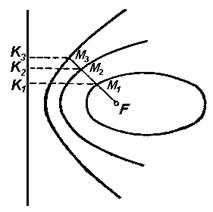
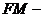
произвольной её точки 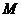
данной точки 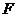
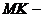
до данной прямой
Обобщая сказанное, можно дать
общее определение конического
сечения (эллипса, гиперболы и
параболы): коническое сечение есть
геометрическое место точек, отношение
расстояний которых до данной точки
(фокуса) и до данной прямой (директрисы) есть величина постоянная 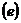
для эллипса 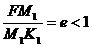
для параболы 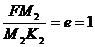
для гиперболы 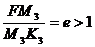
Из (13.5) следует, что при 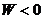
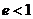
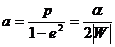
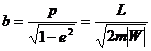
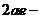
Из уравнения (13.6) следует, что точка с 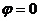
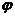
Наименьшее и наибольшее расстояния частицы от центра поля (фокуса эллипса) составляют (из 13.6)
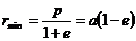
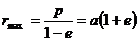
и зависят только от энергии частицы, поскольку из (13.7),
следует, что большая полуось эллипса 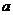
энергии, но не от момента импульса частицы).
Примечание. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце –
первый закон Кеплера.
Время обращения по эллиптической орбите (период 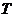
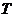
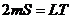
где 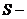
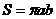
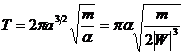
Тот факт, что квадрат периода обращения должен быть пропорционален кубу линейных размеров орбиты, составляет содержание третьего закона Кеплера.
Отметим, что период обращения, как следует из (13.11) зависит только от энергии частицы.
При 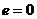
В случае если энергия частицы 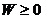
Если энергия частицы положительна 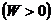
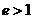
поля определяется выражением
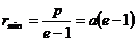
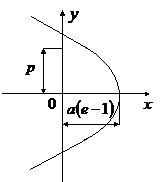
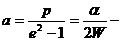
В случае, когда полная энергия частицы
эксцентриситет кривой 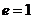
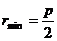
Этот случай реализуется, если частица начинает свое движение
из состояния покоя на бесконечности.
Используя выражение (13.9, 13.12 и 13.14) и соответствующие значения эксцентриситета, можно найти скорость частицы в перигелии при движении по всем рассмотренным траекториям. В точке поворота (перигелии) 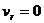
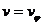
По окружности ( 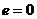
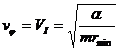
движению по параболе ( 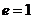
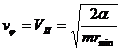
Если скорость частицы лежит в интервале
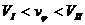
то её траекторией является эллипс ( 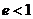
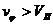
то траектория частицы имеет форму гиперболы ( 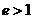
В небесной механике 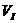
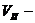
Обратимся теперь к движению в поле отталкивания, в котором потенциальная энергия частицы определяется выражением
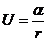
где 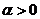
В этом случае эффективная потенциальная энергия частицы
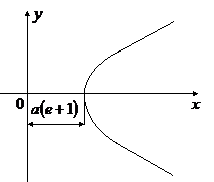
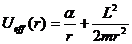
монотонно убывает от бесконечности до нуля
при изменении расстояния от центра поля от нуля до
бесконечности 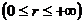
энергия частицы 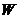
и её движение инфинитно. Все вычисления в этом случае
полностью аналогичны приведенным выше.
Траектория частицы является гиперболой
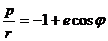
где характеристики кривой по-прежнему определяются
Двигаясь по такой траектории, частица проходит мимо центра поля, как показано на рисунке. Расстояние
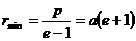
В заключение рассмотрения задачи Кеплера укажем, что при движении в поле центральных сил, котором потенциальная энергия частицы определяется выражением 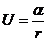
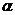
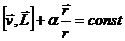
что легко проверить непосредственным вычислением, взяв от него производную по времени.
Сохраняющийся вектор (13.19) направлен вдоль большой оси от фокуса к перигелию и равен по величине 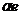
Интеграл движения, наряду с такими сохраняющимися величинами, полная энергия 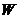
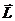
📺 Видео
Урок 218. Напряженность электрического поляСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

Уравнение движения с постоянным ускорением | Физика 10 класс #6 | ИнфоурокСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Уравнение Мещерского, формула ЦиолковскогоСкачать

Урок 65. Движение планет. Законы КеплераСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Урок 106. Реактивное движениеСкачать