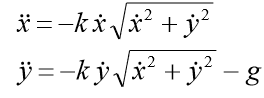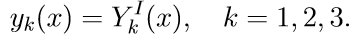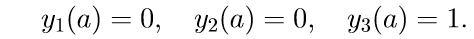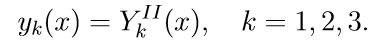Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
- Численное решение математических моделей объектов заданных системами дифференциальных уравнений
- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- Метод и пакет программ для численного решения систем существенно нелинейных интегро-дифференциально-алгебраических уравнений (корректные по Адамару двумерные и трёхмерные краевые задачи) Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Бандурин Николай Григорьевич, Калашников Сергей Юрьевич
- Похожие темы научных работ по математике , автор научной работы — Бандурин Николай Григорьевич, Калашников Сергей Юрьевич
- Method and program package for solution of systems of essentially nonlinear integro-differential-algebraic equations (two- and three-dimensional boundary value problems)
- Текст научной работы на тему «Метод и пакет программ для численного решения систем существенно нелинейных интегро-дифференциально-алгебраических уравнений (корректные по Адамару двумерные и трёхмерные краевые задачи)»
- 📸 Видео
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
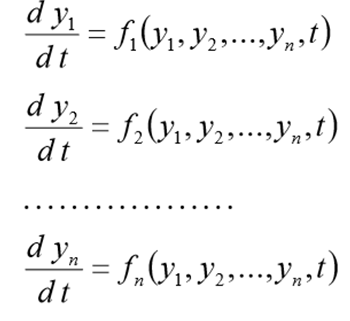
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
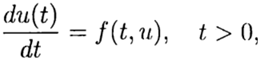

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 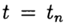

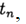


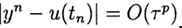

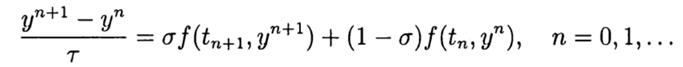
При 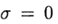
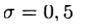
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
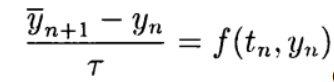
а на этапе корректора (уточнения) — схема
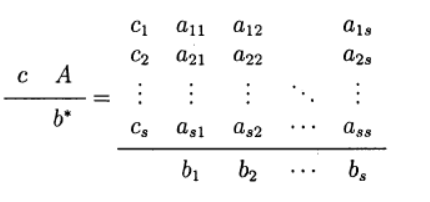
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
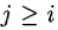

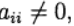

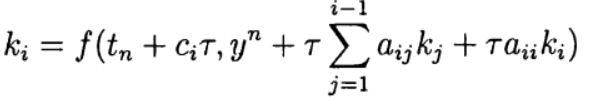
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
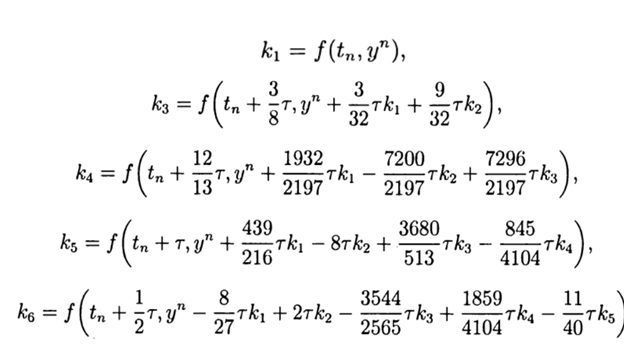
С учётом(9) общее решение имеет вид:
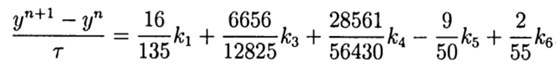
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
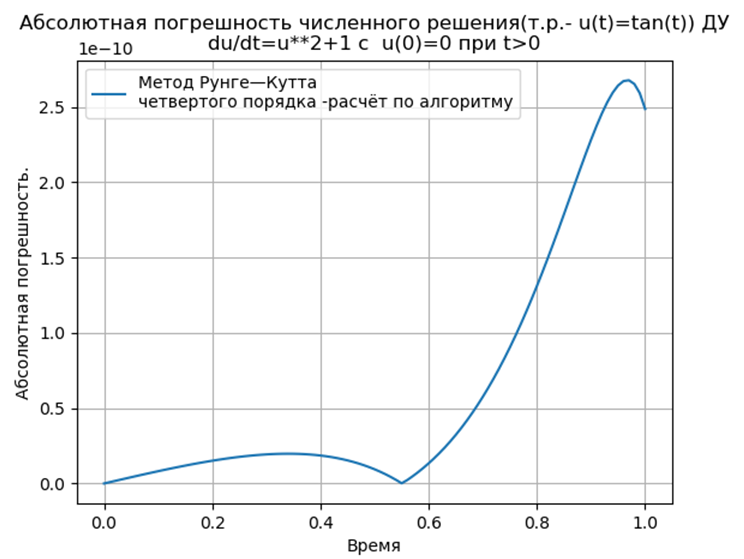
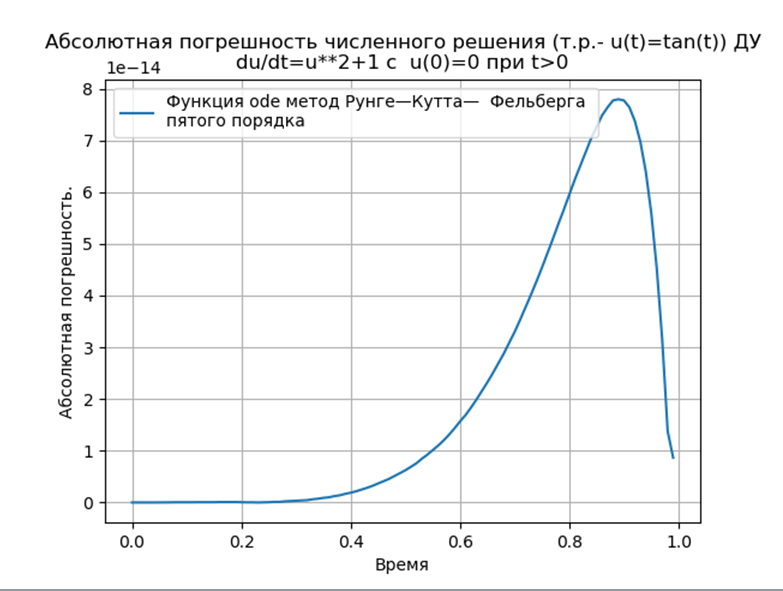
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
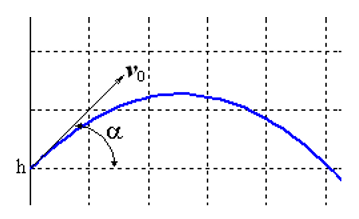
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 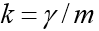
К системе следует добавить начальные условия: 

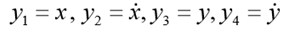
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
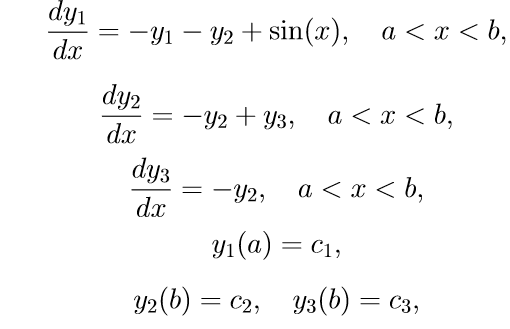
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 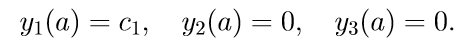
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 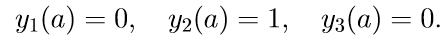
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 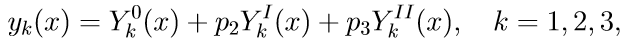
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Метод и пакет программ для численного решения систем существенно нелинейных интегро-дифференциально-алгебраических уравнений (корректные по Адамару двумерные и трёхмерные краевые задачи) Текст научной статьи по специальности « Математика»
Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Аннотация научной статьи по математике, автор научной работы — Бандурин Николай Григорьевич, Калашников Сергей Юрьевич
Кратко описываются метод, алгоритм и пакет программ для решения корректных по Адамару двумерных и трёхмерных задач для систем существенно нелинейных (т. е. не разрешённых относительно старших производных) интегро-дифференциально-алгебраических уравнений . Для приведения последних к системе обычных нелинейных алгебраических уравнений в алгоритме используются полученные ранее формулы интегрирования и дифференцирования. В качестве неизвестных система уравнений может также содержать числовые параметры. Приводятся результаты решения четырёх тестовых примеров.
Видео:Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Похожие темы научных работ по математике , автор научной работы — Бандурин Николай Григорьевич, Калашников Сергей Юрьевич
Видео:14. Операционное исчисление. Система ДУСкачать

Method and program package for solution of systems of essentially nonlinear integro-differential-algebraic equations (two- and three-dimensional boundary value problems)
Goal: the development of method, algorithm and software package for numerical solution of the well-posed (in the sense of Hadamard) twoand three-dimensional problems for the systems of highly nonlinear (i. e., in general, not solved with respect to higher derivatives) integro-differential algebraic equations. Method: contrary to the known methods, based on the procedure of interpolation of the unknown function by algebraic polynomials, an absolutely original approach is applied, which is based on the procedure of interpolation of the derivative of the unknown function. As a result, the necessity is eliminated to use the grid nodes, which do not belong to the domain, where the integration is performed. Consequently, the process of solving highly nonlinear integro-differential algebraic equations can be maximally formalized: it is sufficient to enter the equations in the usual mathematical form and necessary numerical parameters into the computer memory. When solving the partial differential equations, the described procedure is used in the first direction first and then the interpolation procedure in the second direction is performed using the obtained results, etc. The results of the solution of test problems for highly nonlinear integro-differential algebraic equations , which are obtained using the software in automatic mode, i. e. using the minimum of initial data without additional programming, confirm the high accuracy of the suggested approach. Conclusion: the first time in the history of computational mathematics the method is suggested and the first test programs are developed for the automatic solution of the wellposed (in the sense of Hadamard) systems of highly nonlinear integro-differential algebraic equations . Contrary to the all known software packages, the developed software computes and outtypes the node values not only of functions, but also their derivatives and, among them, probably, mixed ones.
Видео:Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать

Текст научной работы на тему «Метод и пакет программ для численного решения систем существенно нелинейных интегро-дифференциально-алгебраических уравнений (корректные по Адамару двумерные и трёхмерные краевые задачи)»
Метод и пакет программ для численного решения систем существенно нелинейных интегро-дифференциально-алгебраических уравнений (корректные по Адамару двумерные и трёхмерные краевые задачи)
Н.Г. Блндурин1, С.Ю. Калашников1
Кратко описываются метод, алгоритм и пакет программ для решения корректных по Адамару двумерных и трёхмерных задач для систем существенно нелинейных (т. е. не разрешённых относительно старших производных) интегро-дифферен-циально-алгебраических уравнений. Для приведения последних к системе обычных нелинейных алгебраических уравнений в алгоритме используются полученные ранее формулы интегрирования и дифференцирования. В качестве неизвестных система уравнений может также содержать числовые параметры. Приводятся результаты решения четырёх тестовых примеров.
Ключевые слова: существенно нелинейные интегро-дифференциальные уравнения, интегро-дифференциально-алгебраические уравнения, численные методы, компьютерные программы.
1. Введение и постановка задачи
Необходимость численного решения краевых задач для систем нелинейных дифференциальных, интегральных и интегро-дифференциально-алгебраических уравнений (ИДАУ), зависящих от двух и более аргументов, часто возникает при математическом моделировании различных физических процессов в науке и технике 6. Наиболее используемым в настоящее время методом для численного решения таких задач является метод конечных разностей 10, на основе которого решаются прикладные задачи математической физики [12, 13]. В связи с развитием вычислительной техники этот метод успешно используется на многопроцессорных системах [14, 15]. Несмотря на то что фундаментальные основы для решения уравнений с частными производными хорошо известны 18, их программная реализация связана со значительными трудностями, поскольку не существует алгоритмов для решения таких уравнений в общем виде, что заставляет исследователей при решении каждой конкретной прикладной задачи в качестве начального шага составлять соответствующую программу и выполнять её отладку. Широко используемые программные комплексы (Maple, Macsyma, Mathematica, Reduce, Matlab и др.), предлагаемые на рынке программных продуктов известными зарубежными корпорациями, не могут быть применены для решения систем существенно
1 Волгоградский государственный архитектурно-строительный университет, Россия Контактный e-mail: bandurin_ng@mail.ru
нелинейных интегро-дифференциально-алгебраических уравнений (СНИДАУ) с частными производными. Ниже кратко описывается предложенный ранее численный метод 28 и приводятся сведения о программах для автоматического решения на ПК корректных по Адамару двумерных и трёхмерных систем, малых по размеру, в общем случае существенно нелинейных интегро-дифференциально-алгебраических уравнений [29], содержащих неизвестные числовые параметры, которые могут входить не только в состав основных уравнений, но и в краевые условия. Области интегрирования рассматриваемых уравнений должны быть ограничены координатными линиями или поверхностями в общем случае криволинейных неортогональных систем координат. Решаются следующие задачи:
— краевые задачи для двумерных систем ИДАУ;
— краевые задачи для трёхмерных систем ИДАУ.
2. Метод решения и программная реализация
Для преобразования интегро-дифференциально-алгебраической задачи к системе нелинейных алгебраических уравнений относительно узловых значений функций, которые затем должны быть решены известными методами, используется формула дифференцирования для функций W, которая в одномерном случае имеет вид [25, 28]
W(r) = ^ Бг(Е — ББ)№— + ВгW,
где W(r), W, I — вектор узловых значений производных функций порядка г, вектор узловых значений функций и единичный вектор соответственно; Б, Б, Е — матрицы интегрирования, дифференцирования и единичная матрица соответственно; и-1 — значения функций и их производных в начальном узле х = х1.
Векторы узловых значений смешанных производных получаются в результате применения формулы дифференцирования к приведенному равенству в другом направлении. Поскольку эта операция является формальной, то повышение порядка производных в системах корректных ИДАУ не влечет за собой появления дополнительных трудностей в программной реализации алгоритма. Следует заметить, что элементы матриц интегрирования и дифференцирования не могут быть записаны в виде формул, используемых для формального программирования, так как представляют собой интегралы и программируются на основе их вычисления [25, 28].
Разработанные для решения систем ИДАУ программы работают на основе минимума исходных данных, т. е. необходимость писать код программы для решения каждой задачи и выполнять её отладку исключается. Для старта итерационного процесса в память ПК следует ввести следующие данные: число уравнений, тексты решаемых уравнений в обычной математической форме, параметры сетки узлов, максимальные значения порядка производных, точное решение задачи (если оно известно) для проверки адекватности вычислений, начальное приближение и краевые условия. Перед заполнением очередной строки исходных данных на дисплей выводится подсказка о содержимом этой строки. После ввода строки выполняется проверка правильности данного содержимого, а в случае обнаружения ошибки ввод прекращается и на экран выводится соответствующее сообщение.
В отличие от всех известных программных комплексов в нашем случае программы вычисляют и выводят на печать узловые значения не только функций, но также и их производных, в том числе, возможно, смешанных.
3. Пакет программ
Пакет состоит из следующих двух отдельных программ.
1. Программа БОиКВБ2 предназначена для численного решения корректных двумерных краевых задач в системе координат (ж, у) для существенно нелинейных систем ИДАУ, которые в своём составе кроме подлежащих вычислению функций могут иметь также неизвестные числовые параметры.
Для успешного численного решения подобных задач принимаются обычные условия и ограничения:
— система уравнений должна быть корректной и не жёсткой;
— число основных ИДАУ должно равняться числу неизвестных функций;
— если система уравнений содержит некоторое число подлежащих вычислению числовых параметров, то к основным уравнениям необходимо добавить соответствующее число дополнительных уравнений, содержащих эти параметры;
— каждое основное и каждое дополнительное уравнение может содержать в своём составе производные любой функции, интегралы и искомые параметры, входящие в подынтегральные выражения интегралов. Предусмотрено использование 10 типов интегралов: два типа с постоянными и переменными верхними пределами и областью интегрирования, совпадающей с областью, на которой ищется решение задачи, остальные восемь типов с постоянными и переменными верхними пределами при интегрировании по четырём координатным линиям, ограничивающим область (эти последние могут быть включены в соответствующие краевые условия);
— для каждой неизвестной функции основные уравнения должны иметь в своём составе по крайней мере одно уравнение с несмешанными производными этой функции наивысшего порядка;
— для каждого неизвестного параметра дополнительные уравнения должны иметь в своём составе уравнение, содержащее данный параметр;
— в области интегрирования решение задачи не должно быть сильно осциллирующим;
— размеры решаемых задач ограничиваются ресурсами ПК.
В области интегрирования предусмотрены два способа формирования сетки узлов, при первом из которых число узлов следует задавать для каждой из осей отдельно, при втором — шаг сетки принимается одинаковым для обеих осей.
2. Программа БОиКВБЗ используется для численного решения существенно нелинейных ИДАУ в системе координат (х,у, г). Условия и ограничения для успешного решения этих уравнений в основном те же, что и для программы БОиКВБ2, но с соответствующими поправками. Например, предусмотрено использование 14 типов интегралов: два типа с постоянными и переменными верхними пределами и областью интегрирования, совпадающей с областью, на которой ищется решение задачи, остальные 12 типов интегралов с постоянными и переменными верхними пределами при интегрировании по шести координатным поверхностям, ограничивающим область.
4. Тестовые примеры
4.1. Краевая задача для трёх нелинейных ИДАУ, содержащая два числовых параметра (решение выполняется по программе BOUNDS2)
Uxxxx + u3 + uxxx sin[2(x + y)] + u cos[a(x + y)] — sin(x + y) = 0, vx + vy + uw — sin(x + y) cos(xy3) — x — y = 0,
w + J j vy (s,t)dsdt + J j xsv(p, — cos(xy3) — x3y3/6 — n3/16 = 0,
a + 4b — b2 + J j xsv(p, — x3y3 — 3 = 0,
b — a + w — cos(xy3) = 0.
Границы области интегрирования 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
/ / u(s, t, 0)dsdt I — sin(x + y) — 1 = 0, 00
u(x,y,n/2) + y J u(s, t, n/2)dsdt + cos x + cos y — 1 = 0. 00
Точное решение u(x, y, z) = sin(x + y — z), v(x, y, z) = x — y + z. Начальное приближение u0(x, y, z) = v0(x, y, z) = 0.
В результате решения максимальное отклонение приближённого решения от точного А получено для второй функции v. Для разных сеток значения этого отклонения были равны:
А(7х7Х7) = 1.7■ 10-4, А(11х11х11) = 1.0■ 10-8, А(7х7х11) = 2.0■ 10-4, А(11х7х7) = 5.6■ 10-5.
В заключение заметим, что, по мнению авторов, в математической литературе не содержится сведений о методах численного решения многомерных систем существенно нелинейных интегро-дифференциально-алгебраических уравнений.
[1] Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977. 535 с.
[2] Пирумов У.Г., Гидаспов В.Ю., Даниелян А.А. и др. Численный анализ двухфазного течения в газодинамическом фильтре // Матем. моделирование. 1998. Т. 10, № 11. С. 19-28.
[3] Головизнин В.М., Коршия Т.К., Самарский А.А. и др. Вариационные схемы магнитной гидродинамики в произвольной системе координат // Вычисл. математика и матем. физика. 1981. Т. 21, № 1. С. 54-68.
[4] Иванова К.Н., Четверушкин Б.Н., Чурбанова Н.Г. Квазигазодинамическая система уравнений и уравнения Навье — Стокса // Матем. моделирование. 2004. Т. 16, № 4. С. 98-104.
[5] Ковеня В.М. Об одном алгоритме решения уравнений Навье — Стокса вязкой несжимаемой жидкости // Вычисл. технологии. 2006. Т. 11, № 2. С. 39-51.
[6] Ичетовкин Д.А., Паасонен В.И. Численное исследование независимой аппроксимации граничных условий на решениях с разрывами производных // Там же. 2010. Т. 15, № 1. С. 77-84.
[7] Шайдуров А.А., Щепановская Г.И., Якубович М.В. Численное моделирование течений вязкого теплопроводного газа в канале // Там же. 2013. Т. 18, № 4. С. 77-90.
[8] Марков А.А. Исчисление конечных разностей. 2-е изд. Одесса: Mathess, 1910.
[9] Гельфонд А.О. Исчисление конечных разностей. М.: Наука, 1967.
[10] Годунов С.К., Рябенький В.С. Введение в теорию разностных схем. М.: Наука, 1973. 400 с.
[11] Волчинская М.И., Гольдин В.Я., Калиткин Н.Н. Сравнительное исследование разностных схем для уравнений акустики // Вычисл. математика и матем. физика. 1974. Т. 14, № 4. С. 919-927.
[12] Шокин Ю.И., Федотова З.И. О достижениях в теории разностных схем // Вычисл. технологии. 1999. Т. 4, № 5. С. 56-69.
[13] Ладонкина М.Е., Милюкова О.Ю., Тишкин В.Ф. Численный метод решения уравнений диффузионного типа на основе использования многосеточного метода // Вычисл. математика и матем. физика. 2010. Т. 50, № 8. С. 1438-1461.
[14] Четверушкин Б.Н. Кинетические схемы и высокопроизводительные многопроцессорные вычисления в газовой динамике // Вычисл. технологии. 2002. Т. 7, № 6. С. 65-89.
[15] Чеванин В.С. Численное моделирование развития гидродинамических неустойчивостей на многопроцессорных системах // Матем. моделирование. 2012. Т. 24, № 2. С. 17-32.
[16] Конторович Л.В., Крылов В.И. Приближённые методы высшего анализа. М.: Гостех-издат, 1949.
[17] Yanenko N.N. Methode a pas Fractionnaires: Resolutions de Problemes Polydimensionnels de Physique Mathematique. Paris: Librairie Armand Colin, 1968. 205 p.
[18] Марчук Г.И. Методы вычислительной математики. М.: Наука, 1980.
[19] Морс Ф.М., Фешбах Г. Методы теоретической физики: Пер. с англ. М.: Мир, 1958.
[20] Березин И.С., Жидков Н.П. Методы вычислений. Т. 2. М.: Физматгиз, 1962. 639 с.
[21] Курант Р. Уравнения с частными производными: Пер. с англ. М.: Мир, 1964. 830 с.
[22] Бахвалов Н.С. Численные методы. Т. 1. М.: Наука, 1973. 631 с.
[23] Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.
[24] На Ц. Вычислительные методы решения прикладных граничных задач. М.: Мир, 1982. 294 с.
[25] Бандурин Н.Г. Новый численный метод порядка n для решения интегро-дифферен-циальных уравнений общего вида // Вычисл. технологии. 2002. Т. 7, № 2. С. 3-10.
[26] Бандурин Н.Г. Большие динамические перемещения и деформации массивной растяжимой нити в движущей среде // Прикладная математика и механика. 2003. Т. 67, № 2. С. 266-271.
[27] Бандурин Н.Г. Численное решение существенно нелинейных интегро-дифференциаль-ных уравнений с запаздывающим аргументом // Вычисл. технологии. 2010. Т. 15, № 3. С. 31-38.
[28] Бандурин Н.Г., Гуреева Н.А. Метод и пакет программ для численного решения систем существенно нелинейных обыкновенных интегро-дифференциально-алгебраических уравнений // Матем. моделирование. 2012. Т. 24, № 2. С. 3-16.
[29] Математическая энциклопедия. Т. 3. М.: Советская энциклопедия, 1982. 951 с.
Поступила в ‘редакцию 18 февраля 2014 г.
Method and program package for solution of systems of essentially nonlinear integro-differential-algebraic equations (two- and three-dimensional boundary value problems)
Bandurin Nikolay G.1, Kalashnikov Sergey Yu.1
Goal: the development of method, algorithm and software package for numerical solution of the well-posed (in the sense of Hadamard) two- and three-dimensional problems for the systems of highly nonlinear (i. e., in general, not solved with respect to higher derivatives) integro-differential algebraic equations.
Method: contrary to the known methods, based on the procedure of interpolation of the unknown function by algebraic polynomials, an absolutely original approach is applied, which is based on the procedure of interpolation of the derivative of the unknown function. As a result, the necessity is eliminated to use the grid nodes, which do not belong to the domain, where the integration is performed. Consequently, the process of solving highly nonlinear integro-differential algebraic equations can be maximally formalized: it is sufficient to enter the equations in the usual mathematical form and necessary numerical
1 Volgograd State University of Architecture and Civil Engineering, 400074, Volgograd, Russia Corresponding author: Bandurin Nikolay G., e-mail: bandurin_ng@mail.ru
parameters into the computer memory. When solving the partial differential equations, the described procedure is used in the first direction first and then the interpolation procedure in the second direction is performed using the obtained results, etc. The results of the solution of test problems for highly nonlinear integro-differential algebraic equations, which are obtained using the software in automatic mode, i. e. using the minimum of initial data without additional programming, confirm the high accuracy of the suggested approach.
Conclusion: the first time in the history of computational mathematics the method is suggested and the first test programs are developed for the automatic solution of the well-posed (in the sense of Hadamard) systems of highly nonlinear integro-differential algebraic equations. Contrary to the all known software packages, the developed software computes and outtypes the node values not only of functions, but also their derivatives and, among them, probably, mixed ones.
Keywords: highly nonlinear integro-differential algebraic equations, numerical methods, computer programs.
📸 Видео
Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Системы дифференциальных уравненийСкачать

Системы дифференциальных уравнений. Часть 2Скачать

Пример решения системы уравнений в MathCAD 14 (34/34)Скачать

Система дифференциальных уравнений. Операционный методСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Системы дифференциальных уравнений. Метод исключенияСкачать

Метод ЭйлераСкачать

Системы дифференциальных уравнений. Часть 1Скачать

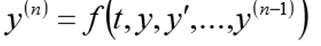
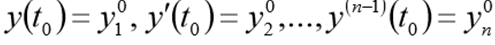


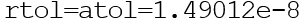
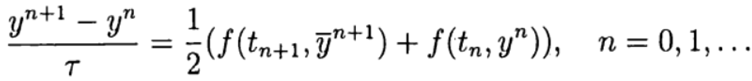
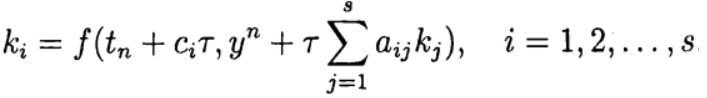
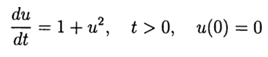 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга