Программа на паскале решение тригонометрических уравнений

Видео:Математика это не ИсламСкачать

Тригонометрические функции Cos и Sin

Подпишись на новости, чтобы ничего не пропустить

Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью — не вся информация вошла в видеоролик.

На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже — в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.

Синтаксис функции Cos:

function Cos(Х : ValReal) : ValReal;

Синтаксис функции Sin:

function Sin(Х : ValReal) : ValReal;

О типе ValReal я рассказывал здесь.

Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.

ВНИМАНИЕ! Не в градусах, а в радианах!

Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.

Формула перевода градусов в радианы проста:

Радиан := Пи * Градус / 180

Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.

Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.

Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.

Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.

Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.

А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.

Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Что такое косинус и синус угла

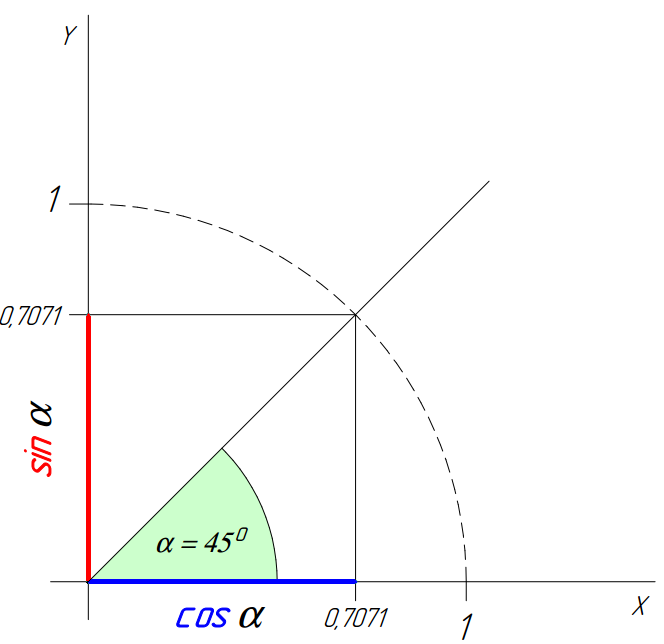
Для начала внимательно посмотрите на рисунок.

Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.

На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).

Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.

В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):

Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:

И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.

И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрические функции в паскале

Ниже приведены тригонометрические функции, используемые в языке программирования Pascal. Их аргумент может быть целым или вещественным; результат в любом случае – вещественный.

1 радиан = 180 / пи

sin(выражение) – синус угла, измеренного в радианах
sin(-pi / 6):4:1. Результат: -0.5
sin(0):4:1. Результат: 0.0
sin(pi / 2):4:1. Результат: 1.0

cos(выражение) – косинус угла, измеренного в радианах
cos(-pi / 6):4:1. Результат: 0.8
cos(0):4:1. Результат: 1.0
cos(pi):4:1. Результат: -1.0

arctan(выражение) – арктангенс
arctan(1e35):8:5. Результат: 1.57080
arctan(0):4:1. Результат: 0.0
arctan(-1):8:5. Результат: 0.78540

Pers.narod.ru. Алгоритмы. Некоторые математические расчёты на Паскале

Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.

Возведение в произвольную степень на Паскале

Требуется вычислить значение с = a b . В зависимости от значений основания a и показателя степени b , вычисление степени может быть реализовано по-разному.

Если a > 0 , а b может принимать произвольные вещественные значения, используем известную формулу a b = exp (b * ln a) :

Если b – целое число (вообще говоря, «не слишком большое» по модулю), а a – любое (не равное нулю при b ), возведение в степень может быть реализовано с помощью цикла:

Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:

Вычисление корня произвольной степени на Паскале

Стандартная функция sqrt умеет извлекать только квадратный корень.

Извлечь корень степени n (где n – натуральное) из числа a можно всегда, кроме случая, когда a и при этом n четно. Извлечь корень степени n из числа a означает возвести число a в степень 1/n . При этом знак корня совпадает со знаком a . Ниже приводится код функции, вычисляющей корень произвольной степени n от своего аргумента a :

Вычисление логарифмов на Паскале

Стандартная функция ln вычисляет только натуральный логарифм. Для вычисления логарифмов по другим основаниям можно применить формулу log _a b = ln b / ln a :

В частности, для вычисления десятичного логарифма lg b можно записать:

Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале

В Паскале имеется стандартная функция arctan для вычисления арктангенса.

Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.

Для вычисления y = arcsin x , где, конечно, |x| , можно применить один из следующих способов:

на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).

Для вычисления z = arccos x , где |x| , можно использовать тот факт, что сумма арксинуса и арккосинуса некоторого значения равна прямому углу:

Вычисление полярных углов на Паскале

Полярным углом точки с координатами (x,y) , отличной от начала координат, называют угол между положительным направлением оси Ox и направлением из начала координат на данную точку. При этом угол отсчитывается против часовой стрелки. Строго говоря, полярный угол не всегда равен arctg (y/x) , это верно лишь при x > 0 . Кроме того, при делении большого значения y на малое x возможно переполнение. Показанная ниже функция вычисляет полярный угол fi , лежащий в промежутке от -pi до +pi , для любой точки с координатами (x,y) , не совпадающей с началом координат:

Проблема с приведением типов на Паскале

Начинающие «паскалисты» нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие «баги». Вот простейший пример.

Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer , а потом «испорченный» результат переписали в переменную типа Longint . ничего не изменит и

Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint . А вот

рулит, получите свои 200000 🙂 Указанная ошибка часто встречается в программах начинающих. Чтобы её не повторять, помните – выражение в Паскале должно быть приведено к нужному типу в процессе его вычисления, а не после его окончания или при присваивании.

Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью – не вся информация вошла в видеоролик.

На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже – в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.

Синтаксис функции Cos:

function Cos(Х : ValReal) : ValReal;

Синтаксис функции Sin:

function Sin(Х : ValReal) : ValReal;

О типе ValReal я рассказывал здесь.

Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.

ВНИМАНИЕ! Не в градусах, а в радианах!

Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.

Формула перевода градусов в радианы проста:

Радиан := Пи * Градус / 180

Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.

Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.

Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.

Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.

Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.

А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.

Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.

Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Что такое косинус и синус угла

Для начала внимательно посмотрите на рисунок.

Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.

На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).

Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.

В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):

Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:

И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.

И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Программирование на Паскале. Тема: «Решение квадратного уравнения с использованием конструкции IF–THEN–ELSE»

Цели урока:

Оборудование:

До сих пор мы с вами говорили о каких-то отвлечённых задачах из области математики. Сегодня мы поговорим о конкретной задаче, которая встречается у вас почти на каждом уроке. Это решение квадратного уравнения. Я хочу, чтобы вы на примере этой задачи поняли, что программирование — это не просто прихоть учителя, это действительно раздел информатики, который может нам помочь, например, в решении конкретных математических задач. Нужно только уметь разбираться в этом.

2. Математическое решение

Давайте вспомним, что понимают под квадратным уравнением?

Что из себя представляют числа a,b,c и как их называют?

С чего начинают решение квадратного уравнения?

Найдите вокруг себя формулу дискриминанта. (D=b 2 -4ac) (Приложение 3)

Как мы решаем далее квадратное уравнение? (сравнение D с нулём)

Какие выводы мы из этого делаем?

(если D 0, то два корня)

Как найти корни квадратного уравнения? Найдите формулы корней среди тех, что развешены повсюду.

Если я случай наличия корней квадратного уравнения сведу к условию D0, то что я получу в случае D=0?

(Два одинаковых корня)

Давайте ещё раз подробно разберём нашу задачу:

Итак, у нас есть квадратное уравнение ax 2 +bx+c=0.

Мы должны решить его, т.е. найти такие значения х, при которых правая часть уравнения =0. Мы знаем, что для этого нам надо:

Найти дискриминант D=b 2 — 4ac.

Сравнить его с нулём

D=b 2 -4ac=10 2 -4*3*3=100 — 36 =64

Х1=,

X2 =

3. Составление блок-схемы алгоритма.

По заданному решению попробуем составить блок-схему алгоритма в тетради. Кто справится первым, прошу к доске.

Подпишем основные элементы блок — схемы применительно к языку программирования.

4. Составление программы по блок — схеме.

Теперь, пользуясь нашими записями, составим программу и покажем её учителю. Тот, кто до конца урока составит только программу, не проверив её на компьютере, получит три, тот, кто наберёт программу на компьютере, но не проверит её на примерах, получит три. Тот, кто выполнит всё задание, получит пять.

А я раздам вам домашнее задание.

Var a,b,c,d,x1,x1: real;

Write(‘введите коэффициенты уравнения a,b,c’); readln(a,b,c);

Else writeln(‘действительных корней нет’)

1. Составить и набрать программу КВУР на компьютере.

Загрузка среды Pascal- 2ЩЛКМ по значку Pascal, нажать ALT+ENTER.

Запуск программы — ЩЛКМ по кнопке RUN выбрать RUN.

2. Решить следующие квадратные уравнения и показать учителю их решения (если нет такой возможности, то занести их в маршрутный лист (Приложение 4)

1,5х 2 -0,6х — 4,8 = 0

3. Переделайте программу КВУР таким образом, чтобы в ней учитывался случай, когда D=0 и уравнение имеет один корень.

4. Закрыть программу.

Подсказка: Меню File — Exit или ALT+X.

1. За простое воспроизведение (набор программы) без проверки оценка «3»

2. За проверку работы программы на примерах, представленных учителем оценка «4»

3. За решение всех заданий и дополнительное изменение программы для случая D=0, оценка «5»

4. Закрыть программу.

Подсказка: Меню File — Exit или ALT+X.

Можно дать дополнительное задание:

Изменить программу так, чтобы ответ был с точностью до 2-х знаков после запятой.

1) Напишите программу проверки пароля. Пусть пароль — некоторое число, зафиксированное в программе. Программа печатает приглашение «введите пароль» и вводит число. Если введённое число совпадает с фиксированным паролем, то программа выводит приветствие, если нет — сообщает о том, что пароль не угадан.

7. Подведение итогов урока.

Итак, ребята, сегодня мы с вами решали конкретные задачи из математики, применяя свои умения по программированию. Вы получили следующие оценки за свои знания. (Перечисление оценок) На следующем уроке нам предстоит познакомиться с новыми алгоритмами — Циклическими.

На сегодня наш урок закончен. До свидания.

Литература:

📹 Видео

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Тригонометрия в ЕГЭ может быть простойСкачать

Программа для решения корней квадратного уравнения с использованием дискриминанта на языке ПаскальСкачать

Решение тригонометрических уравнений и их систем. 10 класс.Скачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ТРИГОНОМЕТРИЯ ЗА 7 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать

Решение тригонометрических уравнений. 10 класс.Скачать

Решение тригонометрических уравнений. 10 класс.Скачать

Все методы решения тригонометрических уравнений за 30 минутСкачать

Урок 1. Первая программа на Pascal (Сложение чисел)Скачать

Занятие 12. Примеры решений тригонометрических уравненийСкачать

Методика решения тригонометрических уравненийСкачать

Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать