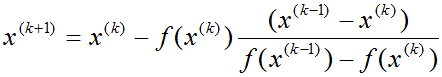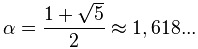Программа для решения уравнений методом хорд (5 видео)

Программирование на C, C# и Java

Содержание

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
Метод хорд
Метод хорд. Алгоритм
Метод хорд. Программная реализация
Метод хорд Pascal (Паскаль)
3 Thoughts to “Метод хорд Pascal (Паскаль)”
Метод хорд
Метод хорд
Метод хорд
📺 Видео

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

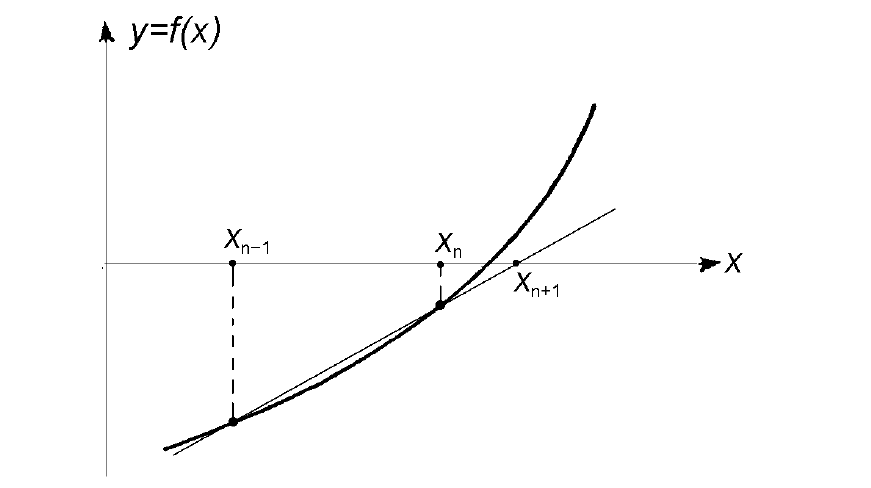
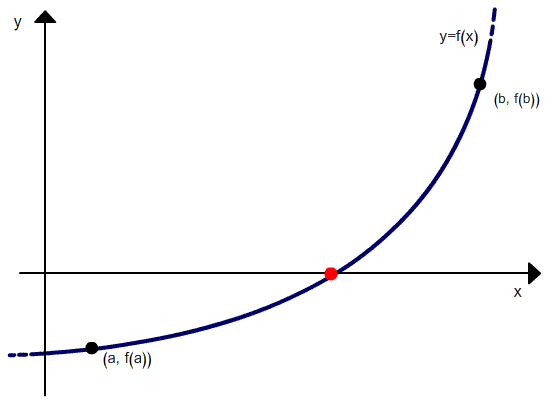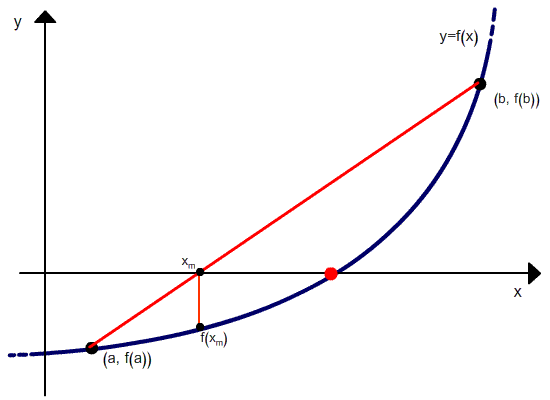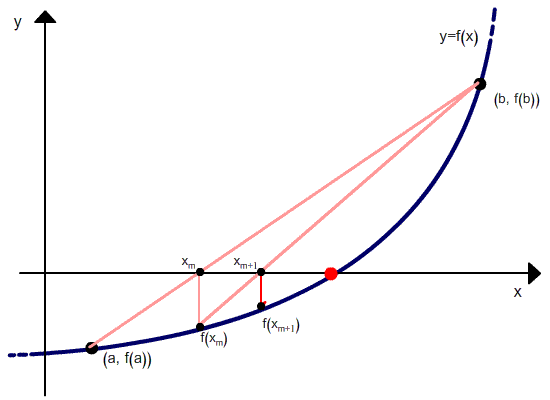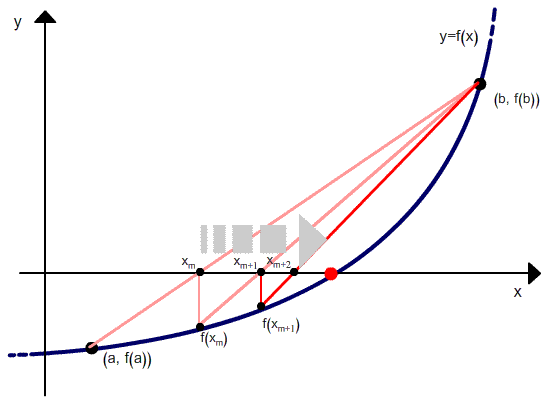
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод хорд Pascal (Паскаль)

Найти корень уравнения методом хорд.

Будем искать корень функции f(x). Выберем две начальные точки C₁(x₁;y₁) и C₂(x₂;y₂) и проведем через них прямую. Она пересечет ось абсцисс в точке (x₃;0). Теперь найдем значение функции с абсциссой x₃. Временно будем считать x₃ корнем на отрезке [x₁;x₂]. Пусть точка C₃имеет абсцисcу x₃ и лежит на графике. Теперь вместо точек C₁ и C₂ мы возьмём точку C₃ и точку C₂. Теперь с этими двумя точками проделаем ту же операцию и так далее, т.е. будем получать две точки C_{n + 1} и C_n и повторять операцию с ними. Таким образом мы будем получать две точки, отрезок, соединяющий которые, пересекает ось абсцисс в точке, значение абсциссы которой можно приближенно считать корнем. Эти действия нужно повторять до тех пор, пока мы не получим значение корня с нужным нам приближением. (источник)

Видео:Метод хордСкачать

3 Thoughts to “Метод хорд Pascal (Паскаль)”

Исправил программу на сайте сделал проще и удобнее
согласно ссылке на сайт с описание алгоритма получается в onlinegdb.com следующая программа,

function f(x:real):real;
begin
f:=x*x*x+x-5;
end;

var xn,xk,p,e:real;
begin
e:=0.001;
xn:=0.5;
xk:=2;
repeat
p:=(f(xk)*xn-f(xn)*xk)/(f(xk)-f(xn));
if abs(f(p)) 0 then xn:=p else xk:=p;
until abs((f(xk)*xn-f(xn)*xk)/f(xk)-f(xn)-p) Atlant

Спасибо retros. Вы меня очень выручили. Буду советовать Ваш ресурс коллегам.

Видео:Метод хорд для приближённого решения алгебраических уравненийСкачать

Метод хорд

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.

Немного теории о методе хорд под калькулятором.

Метод хорд

Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.

Вывод итерационной формулы аналогичен выводу формулы для метода секущих:

Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет

Для точки пересечения с осью абсцисс (у=0) получим уравнение

Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.

Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.

В качестве критерия останова берут один из следующих:

— значение функции на данной итерации стало меньше заданого ε.

— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.