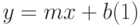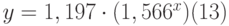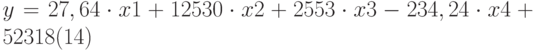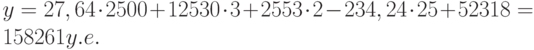Прогноз на основе уравнения регрессии

Уравнения регрессии применимо и для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику не является, строго говоря, корректным и требует проверки условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем.

Ограничением прогнозирования на основании регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится “внешняя среда” протекающего процесса, прежнее уравнение регрессии результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрений может не оказать влияния на урожайность сельскохозяйственной культуры, так как последнюю лимитирует недостаточная влагообеспеченность.

_{Прогнозируемое значение переменной У получается при подстановке в уравнение регрессии ожидаемой величины фактора Х:}

Следует соблюдать одно ограничение: нельзя подставлять значения факторного признака, значительно отличающиеся от входящих в базисную информацию, по которой вычислено уравнение регрессии. При качественно иных уровнях фактора, если они даже возможны в принципе, были бы другими параметры уравнения. Можно рекомендовать при определении значений факторов не выходить за пределы трети размаха вариации, как за минимальное, так и за максимальное значение признака-фактора, имевшееся в исходной информации.

Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его расчетом значения средней ошибки прогноза или доверительного интервала прогноза с достаточно большой вероятностью (надежностью).

_{Доверительные интервалы зависят от следующих параметров:}

_{– отклонение от своего среднего значения ;}

_{В частности для прогноза будущие значения с вероятностью}

_{Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии хорош только в случае, если значение фактора Х не выходит за пределы выборки. Иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.}

Прогнозирование. Регрессионный анализ, его реализация и прогнозирование

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

Сущность метода регрессионного анализа

Одним из методов, используемых для прогнозирования, является регрессионный анализ.

Регрессия – это статистический метод, который позволяет найти уравнение, наилучшим образом описывающее совокупность данных, заданных таблицей.

X	X1	X2	…	Xi	…	Xn
Y	Y1	Y2	…	Yi	…	Yn

На графике данные отображаются точками. Регрессия позволяет подобрать к этим точкам кривую у=f(x), которая вычисляется по методу наименьших квадратов и даёт максимальное приближение к табличным данным.

По полученному уравнению можно вычислить (сделать прогноз) значение функции у для любого значения х , как внутри интервала изменения х из таблицы(интерполяция), так и вне его (экстраполяция).

Линейная регрессия

Линейная регрессия дает возможность наилучшим образом провести прямую линию через точки одномерного массива данных (рис.13.1 а). Уравнение с одной независимой переменной, описывающее прямую линию, имеет вид:

где:x – независимая переменная;

y – зависимая переменная;

m – характеристика наклона прямой;

b – точка пересечения прямой с осью у.

Например, имея данные о реализации товаров за год с помощью линейной регрессии можно получить коэффициенты прямой (1) и, предполагая дальнейший линейный рост, получить прогноз реализации на следующий год.

Нелинейная регрессия

Нелинейная регрессия позволяет подбирать к табличным данным нелинейное уравнение (рис. 13.1 рис. 13.1, б.) – параболу, гиперболу и др. Excel реализует нелинейность в виде экспоненты, т.е. подбирает кривую вида:

,

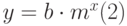
которая позволяет наилучшим образом провести экспоненциальную кривую по точкам данных, которые изменяются нелинейно.

Так, например, данные о росте населения почти всегда лучше описываются не прямой линией, а экспоненциальной кривой. При этом нужно помнить, что достоверное прогнозирование возможно только на участках подъёма или спуска кривой (при отрицательных значениях х), т.к. сама кривая (2) изменяется монотонно, без точек перегиба. Например, делать экспоненциальный прогноз для функции, изменяющейся синусоидально, можно только на участках подъёма или спуска функции, для чего её разбивают на соответствующие интервалы.

Множественная регрессия

Множественная регрессия представляет собой анализ более одного набора данных аргумента х и даёт более реалистичные результаты.

Множественный регрессионный анализ также может быть как линейным, так и экспоненциальным. Уравнение регрессии (1) и (2) примут соответственно вид (3) и (4):

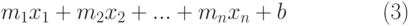( 3)

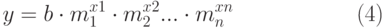( 4)

С помощью множественной регрессии, например, можно оценить стоимость дома в некотором районе, основываясь на данных его площади, размерах участка земли, этажности, вида из окон и т.д.

Использование функций регрессии

В Excel имеется 5 функций для линейной регрессии: ЛИНЕЙН(…)(LINEST), ТЕНДЕНЦИЯ(…), ПРЕДСКАЗ(…), НАКЛОН(…), СТОШУХ(…)) и 2 функции для экспоненциальной регрессии – ЛГРФПРИБЛ(…) и РОСТ(…).

Рассмотрим некоторые из них.

Функция ЛИНЕЙН((LINEST) вычисляет коэффициент m и постоянную b для уравнения прямой (1). Синтаксис функции:

Известные_значения_у и известные_значения_х – это множество значений у и необязательное множество значений х (их вводить необязательно), которые уже известны для соотношения (1).

Константа – это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если константа имеет значение ИСТИНА или опущено, то b вычисляется обычным образом.

Статистика – это логическое значение, которое указывает требуется ли вывести дополнительную статистику по регрессии.

Если статистика имеет значение ЛОЖЬ (или 0), то функция ЛИНЕЙН возвращает только значения коэффициентов m и b , в противном случае выводится дополнительная регрессионная статистика в виде табл. 13.1 таблица 13.1:

Таблица 13.1. Общий вид выводимого массива статистических показателей при использовании функции ЛИНЕЙН((LINEST)

mn	mn-1	…	m2	m1	b
sen	sen-1	…	se2	se1	seb
r 2	sey	…	#Н/Д	#Н/Д	#Н/Д
F	df	…	#Н/Д	#Н/Д	#Н/Д
ssreg	ssresid	…	#Н/Д	#Н/Д	#Н/Д

где: se₁ , se₂,…,se_n – стандартные значения ошибок для коэффициентов m₁ , m₂,…, m_n ;

se_b – стандартное значение ошибки для постоянной b (seb равно #Н/Д, т.е. «нет допустимого значения», если конст. имеет значение ЛОЖЬ);

r 2 – коэффициент детерминированности. Сравниваются фактические значения у и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминированности, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями у. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений у;

se_y – стандартная ошибка для оценки у (предельное отклонение для у);

F – F-cтатистика, или F-наблюдаемое значение. Она используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет;

df – степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надёжности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН;

ss_reg – регрессионная сумма квадратов;

ss_resid – остаточная сумма квадратов;

#Н/Д – ошибка, означающая «нет доступного значения».

Любую прямую можно задать её наклоном m и у-пересечением:

Наклон ( m ). Для того, чтобы определить наклон прямой, обычно обозначаемый через m , нужно взять 2 точки прямой (х1,у1) и (х2,у₂); тогда наклон равен m=(y2-y1)/(x2-x1 ).

у-пересечение ( b ) прямой, обычно обозначаемое через b , является значение у для точки, в которой прямая пересекает ось у.

Уравнение прямой имеет вид: у=mx+b. Если известны значения m и b , то можно вычислить любую точку на прямой, подставляя значения у или х в уравнение. Можно также использовать функцию ТЕНДЕНЦИЯ ( TREND ) (см. ниже).

Если для функции у имеется только одна независимая переменная х, можно получить наклон и у-пересечение непосредственно, используя следующие формулы:

Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точными являются модель, используемая функцией ЛИНЕЙН, и значения, получаемые из уравнения прямой.

В случае экспоненциальной регрессии аналогом функции (5) является функция ЛГРФПРИБЛ(LOGEST):

которая отличается лишь тем, что вычисляет коэффициенты m и b для экспоненциальной кривой (2).

Функция ТЕНДЕНЦИЯ(TREND) имеет вид:

возвращает числовые значения, лежащие на прямой линии, наилучшим образом аппроксимирующие известные табличные данные.

Новые_значения_х – это те, для которых необходимо вычислить соответствующие значения у.

Если параметр новые_значения_х пропущен, то считается, что он совпадает с известными х. Назначение остальных параметров функции ТЕНДЕНЦИЯ совпадает с описанными выше.

В случае экспоненциальной регрессии аналогом функции (7) является функция РОСТ(GROWTH):

возвращает стандартную погрешность регрессии – меру погрешности предсказываемого значения у для заданного значения х.

Правила ввода функций

Формулы(5)-(8) являются табличными, т.е. они заменяют собой несколько обычных формул и возвращают не один результат, а массив результатов. Поэтому необходимо соблюдать следующие правила:

1. Перед вводом одной из формул (5)-(8) выведите блок ячеек, точно совпадающей по размеру с величиной возвращаемого формулой массива результатов. Например, при использовании функции ЛИНЕЙН с выводом статистики нужно выделить массив ячеек, равный табл. 13.1, если параметр статистики равен ЛОЖЬ, достаточно выделить одну строку табл. 13.1.
2. Наберите функцию в строке формул. При этом слова на русском языке можно набирать строчными буквами, т.к. они являются ключевыми и при вводе Exсel автоматически переведет их в заглавные. Имена ячеек автоматически вводятся латинским шрифтом. Вместо слова ИСТИНА можно вводить числа от 1 до 9 (не 0), а вместо слова ЛОЖЬ – число 0. Если в результате, выполнения функции выводится одно число, можно вводить формулы не вручную, а использовать аппарат Мастера функций.
3. Одновременно нажмите клавиши Shift+Ctrl+Enter . Результаты вычислений заполнят выделенные ячейки.

Линия тренда

Excel позволяет наглядно отображать тенденцию данных с помощью линии тренда, которая представляет собой интерполяционную кривую, описывающую отложенные на диаграмме данные.

Для того, чтобы дополнить диаграмму исходных данных линией тренда, необходимо выполнить следующие действия:

• выделить на диаграмме ряд данных, для которого требуется построить линию тренда;
• щелкнуть правой кнопкой мыши и выбрать команду Добавить линию тренда;
• в открывшемся окне задать метод интерполяции (линейный, полиномиальный, логарифмический и т. д.), а также через команду Параметры – другие параметры (например, вывод уравнения кривой тренда, коэффициента детерминированности r 2 , направление и количество периодов для экстраполяции (прогноза) и др.);
• нажать кнопку Закрыть.

Чтобы отобразить на графике (гистограмме и др.) новые, прогнозируемые в результате регрессионного анализа данные, нужно:

• определить их с помощью функции ТЕНДЕНЦИЯ, РОСТ или другим способом,
• выделить на диаграмме нужную кривую, щелкнув по ней правой кнопкой мыши,
• в появившемся окне выбрать команду Выбрать данные…, в появившемся окне выбрать диапазон ячеек с новыми данными вручную или протащив по ним курсор при нажатой левой клавише мыши, нажать ОК.

На диаграмме появится продолжение кривой, построенной по новым данным.

Простая линейная регрессия

Пример 1. Функция ТЕНДЕНЦИЯ(TREND)

а) Предположим, что фирма может приобрести земельный участок в июле. Фирма собирает информацию о ценах за последние 12 месяцев, начиная с марта, на типичный земельный участок. Название первого столбца «Месяц» с данными о номерах месяцев записано в ячейке А1, а второго столбца «Цена» – в ячейке В1. Номера месяцев с 1 по 12 (известные значения х) записаны в ячейки А2…А13. Известные значения у содержат множество известных значений (133 890 руб., 135 000 руб., 135 790 руб., 137 300 руб., 138 130 руб., 139 100 руб., 139 900 руб., 141 120 руб., 141 890 руб., 143 230 руб., 144 000 руб., 145 290 руб.), которые находятся в ячейках В2;В13 соответственно (данные условия). Новые значения х, т.е. числа 13, 14,15,16,17 введём в ячейки А14…А18. Для того чтобы определить ожидаемые значения цен на март, апрель, май, июнь, июль, выделим любой интервал ячеек, например, B14:B18 (по одной ячейке для каждого месяца) и в строке формул введем функцию:

После нажатия клавиш Ctrl+ Shift+Enter данная функция будет выделена как формула вертикального массива, а в ячейках B14:B18 появится результат: .

Таким образом, в июле фирма может ожидать цену около 150 244 руб.

б) Тот же результат будет получен, если вводить в формулу не все массивы переменных х и у, а использовать часть массивов, которые предусматриваются автоматически по умолчанию. Тогда формула (10) примет вид:

В формуле (11) используется массив по умолчанию (1:2:3:4:5:6:7:8:9:10:11:12) для аргумента «известные_значения_х», соответствующий 12 месяцам, для которых имеются данные по продажам. Он должен был бы быть помещен в формуле (11) между двумя знаками ;;. Массив (13:14:15:16:17) соответствует следующим 5 месяцам, для которых и получен массив результатов (146172:147190:148208:149226:150244).

Элементы массивов разделяет знак «:», который указывает на то, что они расположены по столбцам.

в) Аргумент «новые значения х» можно задать другим массивом ячеек, например, В14:В18, в которые предварительно записаны те же номера месяцев 13,14,15,16,17. Тогда вводимая в строку формул функция примет вид =ТЕНДЕНЦИЯ(В2:В13;;В14:В18).

Пример 2. Функция ЛИНЕЙН

а) Дана таблица изменения температуры в течение шести часов, введённая в ячейки D2 :E7 (табл. 13.2 таблица 13.2).

Требуется определить температуру во время восьмого часа.

Таблица 13.2. Данные для примера 1

…	D	E
1	х-№часа	у-t о , град.
2	1	2
3	2	3
4	3	4
5	4	7
6	5	12
7	6	18

Выделим ячейки D8:E12 для вывода результата, введем в строку ввода формулу =ЛИНЕЙН(Е2:Е7;D2:D7;1;1), нажмем клавиши Сtrl+Shift+Enter, в выделенных ячейках появится результат:

3,142857	-3,3333333
0,540848	2,106302
0,894088	2,2625312
33,76744	4
172,8571	20,47619

Таким образом, коэффициент m=3,143 со стандартной ошибкой 0,541, а свободный член b=-3,333 со стандартной ошибкой 2,106, т.е. функция, описывающая данные табл. 13.2 таблица 13.2, имеет вид

Стандартные ошибки показывают максимально возможное отклонение параметра от рассчитанной величины. Для у оно составляет 2,263, т.е. реальное значение у может лежать в пределах .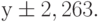

Точность приближения к табличным данным (коэффициент детерминированности r 2 ) составляет 0,894 или 89,4%, что является высоким показателем. При х=8 получим: у=3,143*8-3,333=21,81 град.

б) Тот же результат можно получить, использовав функцию =ТЕНДЕНЦИЯ(Е2:Е7;;G2:G5) для, например, следующих четырёх часов, предварительно введя в ячейки G2 :G5 числа с 7 до 10. Выделив ячейки Н2:Н5, введя в строку формул эту функцию и нажав Сtrl+Shift+Enter, получим в выделенных ячейках массив , т.е. для восьмого часа значение град.

в) Функция ПРЕДСКАЗ ( FORECAST ) – позволяет предсказать значение у для нового значения х по известным значениям х и у, используя линейное приближение зависимости у=f(x).

Для данных примера 2 ввод формулы =ПРЕДСКАЗ(8;Е2:Е7;D2:D7) выводит в заранее выделенной ячейке результат 21,809. Новое значение х может быть задано не числом, а ячейкой, в которую записано это число.

Отличие функции ПРЕДСКАЗ от функции ТЕНДЕНЦИЯ заключается в том, что ПРЕДСКАЗ прогнозирует значения функции линейного приближения только для одного нового значения х.

Экспоненциальная регрессия

Пример 3

а) Функция ЛГРФПРИБЛ.

Рассмотрим условие примера 2.

Поскольку функция в табл. 13.2 таблица 13.2 носит явно нелинейный характер, целесообразно искать ее приближение в виде не прямой линии, как в примере 2, а в виде нелинейной кривой. Из всех видов нелинейности (гипербола, парабола, и др.) Excel реализует только экспоненциальное приближение вида у=b*mx c помощью функции ЛГРФПРИБЛ, которая рассчитывает для этого уравнения значения b и m .

Выделим для результата блок ячеек F8:G12 , введём в строку формул Функцию =ЛГРФПРИБЛ(Е2:Е7;D2:D7;1;1), нажмем клавиши Сtrl+Shift+Enter, в выделенных ячейках появится результат:

1,56628015	1,196513
0,02038299	0,07938
0,99181334	0,085268
484,599687	4
3,52335921	0,029083

Таким образом, коэффициент m=1,566, а b=1,197, т.е. уравнение приближающей кривой имеет вид:

со стандартными ошибками для m, b , и у равными 0,02, 0,079 и 0,085 соответственно. Коэффициент детерминированности r 2 =0,992, т.е. полученное уравнение даёт совпадение с табличными данными с вероятностью 99,2%.

Поскольку интерполяция табл. 13.2 таблица 13.2 экспоненциальной кривой даёт более точное приближение (99,2%) и с меньшими стандартными ошибками для m, b и у, в качестве приближающего уравнения принимаем уравнение (13).

При х=8 получим у=1,197*34,363=41,131 град.

б) Функция РОСТ вычисляет прогнозируемое по экспоненциальному приближению значение у для новых значений х, имеет формат:

Выделим блок ячеек F14: F17 , введём формулу =РОСТ(Е2:Е7;D2:D7;G2:G5;ИСТИНА), в выделенных ячейках появится массив чисел , т.е. при х=8 значение функции у=43,34 град. Это значение немного отличается от вычисленного в п. а), поскольку функция РОСТ использует для расчетов линию экспонециального тренда.

Примечание. При выборе экспоненциальной приближающей кривой следует учитывать, что интерполировать ею можно только участки, где функция монотонно возрастает или убывает (при отрицательном аргументе х), т.е. функцию, имеющую точки перегиба (например, параболу, синусоиду, кривую рис. 2 – т. А и др.) следует разбить на участки монотонного изменения от одной точки перегиба до другой и каждый участок интерполировать отдельно. Для рисунка 2 функцию нужно разбить на 2 участка – от начала до т. А и от т. А до конца кривой.

Множественная линейная регрессия

Пример 4

Предположим, что коммерческий агент рассматривает возможность закупки небольших зданий под офисы в традиционном деловом районе. Агент может использовать множественный регрессионный анализ для оценки цены здания под офис на основе следующих переменных:

у – оценочная цена здания под офис;

х₁ – общая площадь в квадратных метрах;

х₂ – количество офисов;

х₃ – количество входов;

х₄ – время эксплуатации здания в годах.

Агент наугад выбирает 11 зданий из имеющихся 1500 и получает следующие данные:

А	В	С	D	Е
1	х1— площадь, м2	х2 – офисы	х3 – входы	х4 – срок, лет	у – цена, у.е.
2	2310	2	2	20	42000
3	2333	2	2	12	144000
4	2356	3	1,5	33	151000
5	2379	3	2	43	151000
6	2402	2	3	53	139000
7	2425	4	3	23	169000
8	2448	2	1,5	99	126000
9	2471	2	2	34	142000
10	2494	3	3	23	163000
11	2517	4	4	55	169000
12	2540	2	3	22	149000

«Пол-входа» означает вход только для доставки корреспонденции.

В этом примере предполагается, что существует линейная зависимость между каждой независимой переменной (х₁,х₂,х₃,х₄) и зависимой переменной (у), т.е. ценой зданий под офис в данном районе.

• выделим блок ячеек А14:Е18 (в соответствии с табл. 13.1 таблица 13.1),
• введём формулу =ЛИНЕЙН(Е2:Е12;А2:D12;ИСТИНА;ИСТИНА), —
• нажмём клавиши Ctrl+Shift+Enter ,
• в выделенных ячейках появится результат:

А	В	С	D	E
14	-234,237	2553,210	12529,7682	27,6413	52317,83
15	13,2680	530,6691	400,066838	5,42937	12237,36
16	0,99674	970,5784	#Н/Д	#Н/Д	#Н/Д
17	459,753	6	#Н/Д	#Н/Д	#Н/Д
18	1732393319	5652135	#Н/Д	#Н/Д	#Н/Д

Уравнение множественной регрессии теперь может быть получено из строки 14:

Теперь агент может определить оценочную стоимость здания под офис в том же районе, которое имеет площадь 2500 м 2 , три офиса, два входа, зданию 25 лет, используя следующее уравнение:

Это значение может быть вычислено с помощью функции ТЕНДЕНЦИЯ:

При интерполяции с помощью функции

для получения уравнения множественной экспоненциальной регрессии выводится результат:

0,99835752	1,0173792	1,0830186	1,0001704	81510,335
0,00014837	0,0065041	0,0048724	6,033Е-05	0,1365601
0,99158875	0,0105158	#Н/Д	#Н/Д	#Н/Д
176,832548	6	#Н/Д	#Н/Д	#Н/Д
0,07821851	0,0006635	#Н/Д	#Н/Д	#Н/Д
#Н/Д	#Н/Д	#Н/Д	#Н/Д	#Н/Д

Коэффициент детерминированности здесь составляет 0,992 (99,2%), т.е. меньше, чем при линейной интерполяции, поэтому в качестве основного следует оставить уравнение множественной регрессии (14).

Таким образом, функции ЛИНЕЙН, ЛГРФПРИБЛ, НАКЛОН определяют коэффициенты, свободные члены и статистические параметры для уравнений одномерной и множественной регрессии, а функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ, РОСТ позволяют получить прогноз новых значений без составления уравнения регрессии по значениям тренда.

ЗАДАНИЕ

Вариант задания к данной лабораторной работе включает две задачи. Для каждой из них необходимо составить и определить:

1. Таблицу исходных данных, а также значений, полученных методами линейной и экспоненциальной регрессии.
2. Коэффициенты в уравнениях прямой и экспоненциальной кривой (функции ЛИНЕЙН и ЛГРФПРИБЛ), напишите уравнения прямой и экспоненциальной кривой для простой и множественной регрессии.
3. Погрешности (ошибки) прямой и экспоненциальной кривой, вычислений для коэффициентов и функций, коэффициенты детерминированности. Оценить, какой тип регрессии наилучшим образом подходит для вашего варианта задания.
4. Прогноз изменения данных, выполненный с использованием линейной и экспоненциальной регрессии (функции ТЕНДЕНЦИЯ, ПРЕДСКАЗ, РОСТ).
5. Построить гистограмму (или график) исходных данных для задачи 1 (одномерная регрессия), отобразить на ней линию тренда, а также соответствующее ей уравнение и коэффициент детерминированности.

Варианты заданий (номер варианта соответствует номеру компьютера).

1. На рынке наблюдается стойкое снижение цен на компьютеры. Сделать прогноз, на сколько необходимо будет снизить цену на компьютеры в следующем месяце в вашей фирме, чтобы как минимум сравнять её с ценой на аналогичные компьютеры в конкурирующей фирме, если известна динамика изменения цен на них в конкурирующей фирме за последние 12 месяцев.

Для выполнения задания нужно ввести ряд из 12 ячеек с ценами конкурирующей фирмы, сделать прогноз цены на следующий месяц и др. (см. Задание).

1. Известна структура расходов фирмы на рекламу в газетах, на радио, в журналах, на телевидении, на наружную рекламу (в процентах от общей суммы), а также оборот фирмы в каждом за последние 6 месяцев. Какой оборот можно ожидать в следующем месяце, если предполагается следующая структура расходов на рекламу: газеты-40%, журналы-40%, радио-5%, телевидение-14%, наружная реклама-1%.

Для выполнения задания нужно составить таблицу со столбцами вида:

Месяц	х1-газеты,%	х2-журн.,%	х3-рад.,%	х4-телев.,%	х5-нар. рекл.,%	Оборот, $
1	37	34	12	10	5	410000
2	38	37	10	11	6	411500
3	39	38	9	13	7	413700
4	40	39	8	15	8	417050
5	41	40	7	16	9	420000
6	42	42	5	17	10	425000

и сделать множественный регрессионный прогноз (см. Задание).

1. Имеются данные об объеме продаж в расчете на душу населения по хлебу и молоку и данные по годовым доходам на душу за 10 лет. По каждому товару построить модели регрессии для объемов продаж и функции размера доходов. Сделать прогноз о продажах и доходах на следующий год.

Для выполнения задания нужно составить таблицу вида:

Годы	1	2	3	4	5	6	7	8	9	10	11
х1-хлеб, кг	23,5	26,7	27,9	30,1	31,5	35,7	38,3	40,1	41,5	42,8
х2-молоко, л	20,45	22	23,8	25,9	27,4	29	33,5	36,8	38,1	39,5
У-доход, р.	6600	7200	8400	10500	12750	14730	16240	17000	18050	18250

и получить два уравнения – у=f(x1) и у=f(x2), сделать прогноз на следующий год для рядов х₁, х₂, у и др. (см. Задание).

1. Руководство фирмы провело оценку качеств пяти рекламных агентов по следующим признакам: х₁ – эрудиция, х₂ – знание предметной области. Полученные средние оценки, нормированные от 0 до 1, были сопоставлены с оценками эффективности деятельности агентов (% успешных сделок от количества возможных). Определить эффективность для агента с усреднёнными качествами. Сравнить её со средней эффективностью упомянутых 5 агентов.

Исходные данные нужно ввести в таблицу вида:

А	В	С	D	E	F	G
1	х1-эрудиция	х2-энергичность	х3-люди	х4-внешность	х5-знания	Эффективность
2	Агент 1	0,8	0,2	0,4	0,6	1,0	76%
3	Агент 2	0,74	0,3	0,39	0,58	0,95	78%
4	Агент 3	0,67	0,41	0,35	0,5	0,83	79%
5	Агент 6	0,59	0,59	0,33	0,47	0,8	80%
6	Агент 5	0,5	0,7	0,3	0,4	0,74	81%
7	Средняя эффективность пяти агентов
8	Средний агент	0,5	0,5	0,5	0,5	0,5

Массив ячеек В2-F6 заполняется произвольными числами от 0 до 1, столбец G2 -G6 – процентами удачных сделок по принципу «Чем выше уровень качеств агента, тем выше эффективность его работы», в ячейке G7 должна быть формула для вычисления среднего значения ячеек G2:G6 , в ячейке G8 нужно вычислить значение эффективности для среднего агента по формуле, полученной в результате множественного регрессионного анализа работы пяти агентов. Остальные пункты – см. Задание.

1. Автосалон имеет данные о количестве проданных автомобилей «Мерседес» и «БМВ» за последние 4 квартала. Учитывая тенденцию изменения объёма продаж, определить, каких автомобилей нужно закупить больше («Мерседес» или «БМВ») в следующем квартале?

Для выполнения задания нужно составить и заполнить таблицу вида:

Х	1	2	3	4	5
Мерседес ( Y1 )	10	12	15	18
БМВ ( Y2 )	9	10	14	17

сделать прогноз продаж на новый квартал и выполнить другие пункты задания.

1. Известны следующие данные о 5 недавно проданных подержанных автомобилях: у – стоимость продажи, х₁ – стоимость аналогичного нового автомобиля, х₂ – год выпуска, х₃ – пробег, х₄ – количество капитальных ремонтов, х₅ – экспертные заключения о состоянии кузова и техническом состоянии автомобилей (по 10-бальной шкале). Определить, сколько может стоить автомобиль с соответствующими характеристиками: 340 000, 1998г., 140000км., 1, 6 (см. пример 4).

1. Определить минимально необходимый тираж журнала и возможный доход от размещения в нём рекламы в следующем месяце, если известны данные об объёмах продаж этого журнала и доходах от размещения рекламы за последние 12 месяцев (считать, что расценки на рекламу не менялись).

Для выполнения задания нужно составить таблицу вида:

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Тираж,тыс.	100	120	121,7	124,2	128	130,1	133,45	136	141	142,1	143,8	145
Доход,тыс. руб.	128	135	138	142	147	154	159	161	163	168	170,5	172

и заполнить ячейки за 12 месяцев условными данными. По этим данным нужно сделать линейный и экспоненциальный прогноз и др. (см. Задание).

1. В целях привлечения покупателей и увеличения оборота фирма проводит стратегию ежемесячного снижения цен на свой товар. На основании данных о динамике изменения цен, объемов продаж в данной фирме и ещё в 3 конкурирующих фирмах за последние 12 месяцев сделать прогноз о том, возрастает ли объём продаж у данной фирмы при очередном снижении цен в следующем месяце, если предположить, что цены и объёмы у конкурентов в следующем месяце будут средние за рассматриваемый период.

Для выполнения задания нужно составить таблицу вида:

Мес.	Фирма		Конкурент 1		Конкурент 2		Конкурент 3
1	У-объём	х1-цена	х2-объём	х3-цена	х4-объём	х5-цена	х6-объём	х7-цена
2	10000	1875	12000	1720	12500	1740	11970	1700
3	11000	1850	12340	1705	12620	1735	12100	1690
4	11570	1810	12750	1675	12740	1710	12350	1645
5	11850	1750	12910	1630	12960	1695	12500	1615
6	12100	1685	13100	1615	13000	1674	12630	1580
7	12340	1630	13570	1600	13210	1625	12920	1545
8	12750	1615	13820	1575	13320	1610	13150	1520
9	12910	1600	13980	1515	13460	1560	13300	1500
10	13100	1575	14000	1500	13600	1525	13610	1490
11	13230	1530	14070	1495	13780	1500	13850	1485
12	13470	1510	14120	1488	13900	1460	14000	1475
13

1. На основании данных о курсе американского доллара и немецкой марки в первом полугодии сделать прогноз о соотношении данных валют на второе полугодие. Во что будет выгоднее вкладывать деньги в конце года?

Для выполнения задания нужно составить таблицу вида:

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Доллар	24,5	24,9	25,7	26,9	28,0	28,8	29,3	29,7	30,5	30,9	31,8
Марка	72,1	76,3	79,6	85,3	89,7	90,9	93,2	96,4	100,2	101,6	104,9

и сделать линейный прогноз на следующие 6 месяцев и др. (см. Задание).

1. Известны данные за последние 6 месяцев о том, сколько раз выходила реклама фирмы, занимающейся недвижимостью, на телевидении – х₁, радио – х₂, в газетах и журналах – х₃, а также количество звонков –у₁ и количество совершённых сделок – у₂. Какое соотношение количества совершённых сделок к количеству звонков у (в %) можно ожидать в следующем месяце, если известно, сколько раз выйдет реклама в каждом из перечисленных средств массовой информации.

Для выполнения задания нужно составить и заполнить таблицу вида:

A	B	C	D	E
1	месяц	х1	х2	х3	y=у2/у1*100%
2	1	15	10	24	78%
3	2	16	11	23	80%
4	3	18	12	22	81%
5	4	19	12	22	84%
6	5	21	13	21	85%
7	6	22	14	20	89%
8	7

и выполнить применительно к таблице пункты Задания.

1. Для некоторого региона известен среднегодовой доход населения, а также данные о структуре расходов (тыс. руб. в год) за последние 5 лет по следующим статьям: питание – х₁, жильё – х₂, одежда – х₃, здоровье – х₄, транспорт – х₅, отдых – х₆, образование – х₇. На основании известных данных провести анализ потребительского кредита (или накопления) в следующем 6 году.

Для выполнения задания нужно составить и заполнить таблицу вида

Годы	х1	х2	х3	х4	х5	х6	х7	Расход	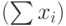Доход	Кредит(Y)
1	5	2	1,3	1	0,3	5	4	18,6	21,4	3,1
2	5,2	2,2	1,2	1,2	0,4	4,8	4,5	19,5	22	2,5
3	5,5	2,5	1,1	1,4	0,6	4,6	4,9	20,6	23,4	2,8
4	5,8	2,7	0,9	1,6	1	4,2	5,6	21,8	25,8	4
5	7	3	0,8	2	1,2	4	6,5	24,7	26,2	1,5
6	7,5	3,3	0,7	2,2	1,5	3,8	7	26,5	27,5

В ячейках столбца ) должны быть записаны формулы, вычисляющие суммы всех расходов х₁+х₂+…+х₇ в каждом году, в ячейках столбца Доход – соответствующие среднегодовые доходы, в ячейках столбца Кредит – формулы разности содержимого ячеек с ежегодными доходами и затратами, т.е. Кредит = Доход- . Затем для столбца Кредит нужно выполнить регрессионный прогноз на следующий год и другие пункты Задания.

1. Для 10 однокомнатных квартир, расположенных в одном районе, известны следующие данные: общая площадь – х₁, жилая площадь – х₂, площадь кухни – х₃, наличие балкона – х₄, телефона – х₅, этаж – х₆, а также стоимость – y . Определить, сколько может стоить однокомнатная квартира в этом районе без балкона, без телефона, расположенная на 1-ом этаже, общей площадью 28 м 2 , жилой – 16 м 2 , с кухней 6 м 2 .

Квартиры	X1	X2	X3	X4	X5	Стоимость ( y )
1	41	33	7	1	2	42000
2	40	30	7,7	2	3	40000
3	45	37	8	0	5	47000
4	46,3	34	9	1	6	49500
5	50	36	9	1	4	51000
6	53	40	9,5	1	7	55000
7	56	41	10	0	9	62000
8	60	47	12	2	10	62300
9	65	49	14	2	12	69000
10	70	58	14,5	2	14	72000
11	28	16	6	0	1

1. Определить возможный прирост населения (кол-во человек на 1000 населения) в 2011 году, если известны данные о кол-ве родившихся и умерших на 1000 населения в 1997-2006 годах.

Годы	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2011
Родились	100	110	130	155	170	174	180	185	190	200
Умерли	108	115	135	160	178	180	186	190	197	205

1. После некоторого спада наметился рост объёмов продаж матричных принтеров. Используя данные об объёмах продаж, ценах на матричные, струйные и лазерные принтеры, а также на их расходные материалы за последние 6 месяцев, определить возможный спрос на матричные принтеры в следующем месяце.

Проанализируйте, связано ли увеличение спроса на матричные принтеры с уменьшением спроса на струйные и лазерные.

Матричные принтеры			Струйные принтеры			Лазерные принтеры
Спрос у1	Цена х1	Рас.мат. z1	Спрос у2	Цена х2	Рас.мат. z/2	Спрос у3	Цена х3	Рас.мат. z3
1	56	4172	174	26	2384	558	13	12517	1558
2	58	4250	179	24	2398	570	11	12984	1612
3	60	4289	182	23	2401	598	9	13259	1789
4	65	4297	194	20	2456	649	8	13687	1865
5	69	4305	205	19	2512	722	7	14013	1998
6	75	4318	213	18	2543	768	6	14587	2200
7	4456	220	17	2601	779	5	14789	2245

Необходимо сделать прогноз на седьмой месяц по уравнению у₁=f(x₁,z₁), получить уравнение y=(у₂,x₂, z₂, у₃, x₃, z₂ ) и проанализировать его. Если слагаемые у₂ и у₃ входят в регрессионное уравнение со знаком «-«, то уменьшение спросов у₂ и у₃ ведёт к увеличению спроса у₁.

1. Построить прогноз развития спроса населения на телевизоры, если известна динамика продаж телевизоров (тыс. шт.) и динамика численности населения (тыс. чел.) за 10 лет. По данным таблицы сделать прогноз по обоим рядам на следующий год. Выполнить другие пункты задания.

Годы	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011
Динамика населения (тыс. чел)	21,5	26,1	31,5	34,9	45,1	50,8	56	59,4	63,9	67,1
Динамика продаж (тыс. шт.)	2,5	2,9	3,4	3,9	4,1	4,8	5	5,6	5,9	6,2

1. Размещая рекламу в 4-х изданиях, фирма собрала сведения о поступивших на нее откликов – у и сопоставила их с данными об изданиях: х₁ – стоимость издания, х₂ – стоимость одного блока рекламы, х₃ – тираж, х₄ – объём аудитории, х₅ – периодичность, х₆ – наличие телепрограммы. Какое количество откликов можно ожидать на рекламу в издании со следующими характеристиками: 15000 руб., 10$, 1000 экз., 25000 чел., 4 раза в месяц, без телепрограммы.

Пользуясь данными таблицы

Издания	х1	х2	х3	х4	х5	х6	Отклики, у
1	10000	13	700	15000	4	1	108
2	12500	12	850	22000	8	1	115
3	15890	11,8	960	28000	10	0	120
4	17850	11	1200	32000	26	1	128
5	15000	10	1000	25000	4	0

необходимо сделать прогноз при заданных характеристиках.

1. Размещая свою рекламу в 2-х печатных изданиях одновременно, фирма собрала сведения о количестве поступивших звонков и количестве заключенных сделок по объявлениям в каждом из указанных изданий за последние 12 месяцев. Определить, в каком из изданий и насколько эффективность размещения рекламы в следующем месяце будет больше?

Месяцы	Издание 1		Издание 2
Звонки	Сделки	Звонки	Сделки
1	98	66	112	79
2	105	72	143	85
3	105	75	150	90
4	110	80	130	100
5	125	90	120	75
6	140	100	115	80
7	136	95	128	82
8	137	87	132	78
9	145	102	138	88
10	123	75	143	92
11	130	79	150	97
12	139	88	155	97
13

Эффективность определяется как сделки/звонки. Сделать линейный и экспоненциальный прогнозы по обоим изданиям.

1. Пусть комплект мягкой мебели (диван + 2 кресла) характеризуется стоимостью комплектующих: х₁— деревянные подлокотники, х₂ – велюровое покрытие, х₃ – кресло-кровать, х₄ – угловой диван, х₅ – раскладывающийся диван, х₆ – место для хранения белья. По данным о стоимости 5 комплектов сделать вывод о возможной стоимости комплекта с обычным раскладывающимся диваном, с местом для белья, без деревянных подлокотников и велюрового покрытия, с креслом кроватью.

Пользуясь данными таблицы

Признаки	х1	х2	х3	х4	х5	х6	У -стоимость
Комплект 1	250	540	2500	4300	6400	800	13850 руб.
Комплект 2	320	650	3000	4800	7000	980	15770 руб.
Комплект 3	400	730	3900	6000	8500	1100	16730 руб.
Комплект 4	452	1300	4300	7500	9200	2050	24350 руб.
Комплект 5	550	1750	6400	12450	16700	4300	42150 руб.
Комплект 6	670	800	2750	6700	8800	1000

сделать прогноз и выполнить другие пункты задания.

1. Для 2-х радиостанций известны данные об изменении объёма аудитории и динамике роста цен за 1 минуту эфирного времени за последние 12 месяцев. Определить, для какой радиостанции стоимость одного контакта со слушателем будет меньше?

Месяц	Радиостанция 1		Радиостанция 2
Аудитория	Цена 1 мин.	Аудитория	Цена 1 мин.
1	250000	8000	300000	7560
2	540000	6500	450000	6340
3	580000	6460	490000	6250
4	650000	6300	550000	6000
5	730000	6060	610000	5730
6	750000	6000	690000	5300
7	800000	5400	750000	5100
8	840000	5320	780000	5000
9	890000	5130	870000	4700
10	950000	5000	900000	4650
11	1000000	4800	940000	4600
12	1108000	4700	1025000	4540
13
Контакт

В строке «Контакт» в ячейках С8 и D8 должны быть записаны формулы = С7/В7 и =Е7/D7 соответственно, вычисляющие стоимость 1 мин. Эфира для одного слушателя в прогнозируемом месяце. Прогноз нужно выполнить для линейного и экспоненциального приближений и выбрать более достоверный, а также сделать другие пункты Задания.

1. На основании данных ежемесячных исследований известна динамика рейтинга банка (в условных единицах) за последние 6 месяцев в следующих сферах:
2. менеджмент и технология – х₁;
3. менеджеры и персонал – х₂;
4. культура банковского обслуживания – х₃;
5. имидж банка на рынке финансовых услуг – х₄;
6. реклама банка – х₅.

Определить возможное изменение количества вкладчиков данного банка в следующем месяце, если известны значения сфер рейтинга и количество вкладчиков в каждом из рассматриваемых 6 месяцев.

Практический пример построения прогноза на основе регрессионного анализа.

Специалист планово-экономического отдела (ПЭО) машиностроительного завода изучает цены и объемы продажи изделия, выбрав произвольным образом десять недель. Собранные им данные представлены в табл. 4.2.

Данные о продаже изделия

Номер недели	Количество проданного изделия (тыс. шт) — Y	Цена одного изделия (усл. ед) — Х
1,3
2,0
1,7
1,5
1,6
1,2
1,6
1,4
1,0
1,1

Этап 1. Для наглядного изображения исходных данных и дальнейшего анализа и прогнозирования составляется диаграмма рассеивания для исходных данных, представленная на рис. 4.3.

Рис. 4.3. Диаграмма рассеивания

Диаграмма показывает, что имеет место обратная линейная зависимость между переменной Y (количеством проданных изделий) и переменной X (ценой одного изделия). Можно сделать вывод, что при возрастании цены объем продаж уменьшается.

Таким образом, далее целесообразно оценить количественную меру обнаруженной зависимости. Для этого вычисляется выборочный коэффициент корреляции на основе формулы 4.19.

. (4.19)

Вспомогательные расчеты представляются в таблице 4.3.

Расчеты коэффициента корреляции

n=10	Y	X	XY	Y 2	Х 2
10,0	1,3	13,00	100,00	1,69
6,0	2,0	12,00	36,00	4,00
5,0	1,7	8,50	25,00	2,89
12,0	1,5	18,00	144,00	2,25
10,0	1,6	16,00	100,00	2,56
15,0	1,2	18,00	225,00	1,44
5,0	1,6	8,00	25,00	2,56
12,0	1,4	16,80	144,00	1,96
17,0	1,0	17,00	289,00	1,00
20,0	1,1	22,00	400,00	1,21
Сумма	112,0	14,4	149,30	1488,00	21,56

.

Расчеты коэффициента корреляции достаточно просто можно провести в Excel: Сервис → Анализ данных → Корреляция.

По результатам расчетов значение выборочного коэффициента корреляции, равное -0,86, указывает на довольно тесную обратную зависимость между переменными Y и Х, т.е. при возрастании цены одного изделия количество продаваемых изделий падает.

При этом возникает следующий вопрос: на сколько уменьшается продажа изделий при увеличении его цены? В данном случае на диаграмме рассеивания можно провести прямую, проходящую достаточно близко от отмеченных точек. Тогда наклон прямой покажет, на сколько изделий в среднем будет уменьшаться величина Y при увеличении величины Х на одну усл. ед.

Этап 2.Провести требуемую прямую, визуально сориентировав ее так, чтобы она находилась как можно ближе к отмеченным на диаграмме точкам, можно по-разному. Необходим такой способ нахождения прямой наилучшего приближения, при использовании которого любой человек будет получать один и тот же результат для заданного набора данных. Для однозначного определения прямой наилучшего приближения чаще всего применяется критерий наименьших квадратов.

С помощью метода наименьших квадратов вычисляются оценки коэффициентов регрессии для данных специалиста ПЭО. Вычисления проводятся на основе уравнений 4. 3 и 4. 4, а также числовых значений из табл. 4.3. Определяется следующее:

,

.

Тогда уравнение прямой регрессии, определенное по методу наименьших квадратов, будет иметь следующий вид:

. (4.21)

Смысл коэффициентов из этого уравнения: свободный член — это значение Y при X, равном нулю. Формально интерпретируя уравнение, получаем, что при Х = 0 (т.е. при нулевой стоимости изделия) среднее количество продаваемых изделий будет равно 32 140. Это не соответствует здравому смыслу. Данная проблема связана с прогнозом значений Y для значений X,заметно отличающихся от тех, которые представлены в выборке данных. Так, в выборке нет величин X, близких к нулю. В этой ситуации, как и во многих других случаях применения регрессионного анализа, разумная интерпретация свободного члена уравнения регрессии не представляется возможной.

В общем случае неразумно прогнозировать значения Y для тех X, которые лежат вне множества значений переменной X, встречающихся в выборке. Функцию регрессии следует считать подходящей аппроксимацией реальной ситуации только в той области, из которой взяты анализируемые данные. Экстраполяция функции вне этой области возможна только при справедливости достаточно ограничивающего предположения о том, что характер зависимости Y от X при этом не изменяется.

Угловой коэффициент можно интерпретировать как среднее изменение величины Y при возрастании Х на единицу. В данном примере Y в среднем уменьшается на 14 540 (т.е. будет продано на 14 540 тыс. шт. меньше) при возрастании X на единицу (т.е. при возрастании цены изделия на одну усл. ед.). Каждое увеличение цены на одну усл. ед. уменьшает объем продажи в среднем на 14 540 изделий, т.е. наша выборка показывает, что увеличение цены на одну усл. ед. уменьшает количество продаваемых изделий на 14,54.

Связь значений переменных X и Y может быть проиллюстрирована на диаграмме рассеивания путем проведения прямой, являющейся наилучшим приближением этой зависимости (рис. 4.4).

Рис. 4.4. Данные прогноза

Обратите внимание на то, что вертикальные отрезки от точек данных до прямой проведены пунктиром. Сумма квадратов длин отрезков, проведенных к этой прямой, должна быть меньше аналогичной суммы квадратов длин, проведенных к любой другой прямой. (Для данных специалиста ПЭО сумма квадратов длин равна SSЕ = 59,14). Из мето­да наименьших квадратов следует, что данная прямая является наилучшим приближением для заданных 10 точек исходных данных.

Этап 3.Определение стандартной ошибки.

Для данных специалиста ПЭО стандартная ошибка оценки равна следующему:

.

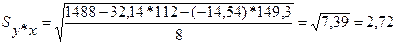
Для величины Y принимающей значения от 3 до 18 (рис. 4.4), значение = 2,72 до­вольно велико и указывает, что существенная часть вариации величины Y (количества проданных изделий) не объясняется изменением величины X (цены). Это утверждение будет исследовано позже.

Этап 4. Прогнозирование величины Y.

Предположительно специалист хочет получить прогноз количества изделий, которое будет продано при цене 1,63 усл. ед. за штуку. Из уравнения (4.21) получается 8440 штук.

.

Данный прогноз — это значение величины Y. Поэтому интересующий прогноз будет координатой Y точки с координатой X = 1,63 на регрессионной прямой.

Конечно, реальные значения величины Y, соответст­вующие рассматриваемым значениям величины X, к сожалению, не лежат в точности на регрессионной прямой. Фактически они разбросаны относительно прямой в соответствии с величиной . Более того, выборочная (построенная графически) регрессионная прямая является оценкой регрессионной прямой генеральной совокупности, основанной на выборке всего лишь из 10 пар данных. Другая случайная выборка 10 пар данных даст иную выборочную прямую регрессии; это аналогично ситуации, когда различные выборки из одной и той же генеральной совокупности дают различные значения выборочного среднего.

Графически 95%-ный интервал прогноза значений Y для данных специалиста представлен на рис. 4.5.

Y

Рис. 4.5. 95%-ный интервал прогноза значений Y

Используя результаты из табл. 4.3 и уравнения 4.11, где X =1,44 , определяется стандартная ошибка прогноза в точке X = 1,63.

Расчет стандартной ошибки прогноза

X
1,3	0,0196
2,0	0,3136
1,7	0,0676
1,5	0,0036
1,6	0,0256
1,2	0,0576
1,6	0,0256
1,4	0,0016
1,0	0,1936
1,1	0,1156

.

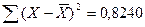При и X=1,63, используя уравнение 11, определяется 95%-ный интервал прогноза значений Y:

=8,44 2,306*2,91=8,44 6,71

или (1,73;15,15), т.е. от 1730 до 15150 штук.

Здесь 2,306= — это нижний 2,5%-ый квантиль; t – распределения с 8 степенями свободы.

Интервал прогноза настолько велик, что практически бесполезен для прогнозирования значений величины Y. Это связано с тем, что исходная выборка мала, а значение 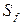сравнительно велико. Степень неопределенности, представленная большим интервалом прогноза, не видна по отдельным точечным прогнозам, полученным из функции регрессии. Значительным преимуществом интервальной оценки является явное отражение неопределенности, связанной с прогнозом.

Вообще говоря, опасно использовать регрессионную функцию для предсказания значений величины Y вне области имеющихся данных. Специалист вполне оправданно пытается получить прогноз для величины Y при Х= 1,63, поскольку некоторые из имеющихся в исходных данных значений X близки к 1,63. С другой стороны, нельзя прогнозировать значение Y при X=3,00. Среди исходных данных нет таких больших значений X и поэтому любой прогноз значения Y для подобного значения X очень сомнителен. При попытке оценить количество изделий, которое может быть продано по цене 3 усл. ед. за штуку, специалист должен исходить из предположения, что при подобных значениях цены линейная модель остается верной. У него могут быть определенные причины считать так, однако никаких явных свидетельств этого не существует.

Этап 5.Разложение дисперсии.

Специалист ПЭО начал свой анализ данных с информации об объемах продаж только за 10 недель (переменная Y). Если другой информации не поступит, он может использовать выборочное среднее Y=11,2 как прогноз количества продаваемых изделий для каждой недели. Ошибки или отклонения, связанные с этим прогнозом, равны Y — , и сумма квадратов ошибок даст . Последнее значение, ,в точности равно SST, обшей сумме квадратов, введенной в уравнение 5.10. Таким образом, SSТ измеряет отклонение значе­ния Y от прогноза, использующего лишь значения Y в его вычислении. (Если анализ остановить на этом этапе, отклонения Y следует измерять выборочной дисперсией вместо SST= . Выборочная дисперсия является обычной мерой из­менчивости наблюдений одной переменной.) Прогноз величины , значения отклонения Y — суммы квадратов SST= приведены в табл. 4.5. (Сумма отклонений Y — всегда равна нулю, поскольку среднее является математическим центром значений Y).

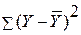
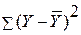
Отклонения для данных прогноза и значения прогноза

Данные Y	Прогноз Y ( )	Отклонения (Y- )	(Y- ) 2
11,2	-1,2	1,44
11,2	-5,2	27,04
5,0	11,2	-6,2	38,44
12,0	11,2	0,8	0,64
10,0	11,2	-1,2	1,44
15,0	11,2	3,8	14,44
5,0	11,2	-6,2	38,44
12,0	11,2	0,8	0,64
17,0	11,2	5,8	33,64
20,0	11,2	8,8	77,44
Сумма:	0,0	233,6

Прогнозист также имеет информацию о значениях переменной X (о цене одного изделия), соответствующих величинам Y. (r = -0,86.) Можно ожидать, что с помощью этой дополнительной переменной мы сможем объяснить часть изменчивости (разностей) значений Y, не объясненной прогнозом .

По расчетам линейный прогноз пар значений Х-Y задается уравнением = 32,14 — 14,54X. Таблица, подобная табл. 5.5, может быть построена при в качестве прогноза значений Y.Результат приводится в табл. 4.6. (Если свободный член включен в уравнение регрессии, сумма отклонений всегда равна нулю).

Отклонения для данных при значении прогноза

X	Y	Прогноз Y ( ), использующий уравнение	Отклонения (Y- )	(Y- ) 2
1,3	10,0	13,238	-3,238	10,485
2,0	6,0	3,06	2,940	8,644
1,7	5,0	7,422	-2,422	5,866
1,5	12,0	10,33	1,670	2,789
1,6	10,0	8,876	1,124	1,263
1,2	15,0	14,692	0,308	0,095
1,6	5,0	8,876	-3,876	15,023
1,4	12,0	11,784	0,216	0,047
1,0	17,0	17,6	-0,600	0,360
1,1	20,0	16,146	3,854	14,853
Сумма:	0,0	59,41

Сравнение табл. 4.5 и 4.6показывает, что использование в качестве прогноза значения Y приводит, вообще говоря, к меньшим отклонениям (по абсолютной величине) и существенно меньшим суммам квадратов остатков (ошибок), чем применение для прогноза значения . Использование соответствующих значений X уменьшает ошибку прогноза (предсказания). Таким образом, знание значений X помогает лучше объяснить разности Y. Но в какой мере может помочь знание значений X? Ответ на этот вопрос можно получить посредством раз­биения изменчивости.

Используя данные из табл. 4.5, 4.6 и уравнение 4.14, имеется

SST= 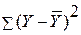=233,6;

SSE= =59,41

SSR= = SST- SSE = 233,6 — 59,41 = 174,19.

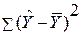
Разбиение изменчивости является следующим:

SST =	SSR +	SSE
233,6 =	174,19 +	59,41
Общая вариация	Объясненная вариация	Необъясненная вариация

Для изменчивости, оставшейся после предсказания Y через значение , специалист по­лучил следующее значение:

.

Это та часть, которая объясняется взаимосвязью значений Y и X. Доля вариации Y относительно , равная 1 – 0,75 = 0,25, осталась необъясненной. С этой точки зрения знание значений соответствующей переменной X приводит к лучшему прогнозу значений Y, чем прогноз, полученный из значения , не зависящего от Х.

Разбиение изменчивости для данных прогноза может быть представлено в таблице анализа дисперсии ANOVA, общий вид которой представлен в табл. 4.1., 4.7.

Таблица ANOVA по данным прогноза

Источник	Сумма квадратов	Степени свободы	Среднеквадратическое отклонение
Регрессия	174,19	174,19
Ошибки	59,41	7,43
Общая	233,6

Разбиение изменчивости ясно показано в столбце с суммами квадратов. Необходимо обратить внимание на то, что с учетом погрешности округления MSE=7,43=(2,72) 2 = .

Этап 6.Расчеткоэффициента детерминации r 2 .

Для данных прогнозиста коэффициент был вычислен ранее. Значение коэффициента детерминации также можно легко получить из таблицы ANOVA, представленной табл. 5.7.

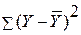
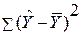
SST= =233,6; SSR= = 174,19; SSE= =59,41

и r 2 = .

Кроме того, r 2 можно вычислить следующим образом:

r 2 = .

Около 75% изменчивости количества проданных штук изделий (Y) можно объяснить разницей в цене изделия (X). Около 25% изменчивости количества проданного молока нельзя объяснить изменением цены. Эта часть изменчивости может быть объяснена влиянием фак­торов, не учтенных в проведенном регрессионном анализе (например, рекламой, возможно­стью замены изделий, качеством материалов и т.п.).

В случае прямолинейной регрессии коэффициент детерминации r 2 равен квадрату коэффициента корреляции r:

коэффициент детерминации = (коэффициент корреляции) 2 ,

Значит для данных специалиста, с учетом погрешности округления,

Почему в регрессионном анализе коэффициенты r и r 2 необходимо рассматривать отдельно? Причина в том, что они несут различную информацию.

Коэффициент корреляции выявляет не только силу, но и направление линейной связи. В случае данных, собранных прогнозистом, имеет место отрицательная взаимосвязь (r = -0,86). В других случаях значение r может указывать на положительную взаимосвязь. Когда существует дело с большим набором переменных, иногда полезно учитывать характер взаимосвязи в некоторых парах переменных. Следует отметить, что когда коэффициент корреляции возводится в квадрат, полученное значение всегда будет положительным и информация о характере взаимосвязи теряется.

Коэффициент детерминации r 2 измеряет силу взаимосвязи между Y и X иначе, чем коэффициент корреляции r. Значение r 2 измеряет долю изменчивости Y, объясненную разницей значений X. Эту полезную интерпретацию можно обобщить на взаимосвязь между Y и более чем одной переменной X.

На рис. 4.6 иллюстрируется два крайних случая для значения коэффициента r 2 : r 2 = 0 и r 2 =1. В случае (а) изменчивость Y никак не объясняется изменениями X: диаграмма рассеивания не показывает никакой линейной взаимосвязи между значениями величин X и Y. В случае (б), когда коэффициент r 2 = 1, изменчивость Y полностьюобъясняется, если известны значения X: все точки данных в нашей выборке лежат на прямой регрессии.

X

а) линейная корреляция отсутствует б) четко выраженная линейная корреляция

Рис. 4.6. Интерпретация крайних значений коэффициента детерминации r 2

Примечание. Проведенные расчеты представленных и прогнозируемых данных по всем пунктам можно проверить с помощью компьютерных расчетов в Excel – функции регрессионного анализа.

Задание лабораторной работы.

Примечание. В большинстве из приведенных ниже упражнений представлены данные, предназначенные для обработки с помощью процедур регрессионного анализа. Хотя в одном или двух случаях возможно, и даже полезно, выполнение необходимых вычисле­ний вручную, для студента важно научиться использовать компьютер для решения подобных задач.

Общие задания для выбранных по вариантам задач.

1. Существует ли значимая взаимосвязь между рассматриваемыми показателями Х и Y, пояснить какая.

2. Построить диаграмму рассеивания для имеющихся данных.

3. Вычислить коэффициент корреляции и интерпретировать его значения.

4. Определить регрессионную прямую методом наименьших квадратов.

5. Проверить значимость углового коэффициента на 5%-ном уровне значимости. Является ли значимым коэффициент корреляции? Объяснить полученные результаты.

6. Определить уравнение регрессии.

7. Построить таблицу ANOVA, рассмотреть остатки.

8. Составьте отчет, содержащий объяснения по результатам выполненного анализа.

Вариант 1. Рассмотрите данные в табл. 4.8., где в столбце X приведены суммы еженедельных расходов на рекламу АЗС, а в столбце 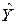— еженедельный объем продаж. Используя эти данные, ответьте на вопросы 1, 7, 8.

Y (усл. ед.)

Х(усл. ед.)

Y (усл. ед.)

Х (усл. ед.)

Необходимо определить уравнение для расчета прогноза результирующего показателя. Какой процент вариаций показателя Х, Y объясняется уравнением прогноза? Составить прогноз показателя Y при составляющих (п+1) значения (выбор значения Х произвольное).

Определить величину необъясненной и общей вариации.

Вариант 2. Сведения о времени, затраченном на обслуживание станка, и соответствующих объемах произведенных изделий приведены в табл. 4.9. Используя эти данные, ответить на вопросы 1,2,3,5,7,8.

Время обслуживания (мин.)	Объем изделий (усл. ед.)	Время обслуживания (мин.)	Объем изделий (усл. ед.)
3,6	30,6	1,8	6,2
4,1	30,5	4,3	40,1
0,8	2,4	0,2	2,0
5.7	42,2	2,6	15,5
3,4	21,8	1,3	6,5

Вычислить точечную и 99%-ную интервальную оценку величины Y при Х= 3,0.

Вариант 3. Служащему автобусного парка необходимо определить, существует ли положительная взаимосвязь между годовыми расходами на содержание автобуса и сроком его эксплуатации. Если подобная взаимосвязь будет обнаружена, он сможет лучше планировать размер годового бюджета автобусного парка. Им собраны данные, приведенные в табл. 4.10. Используя эти данные, ответьте на вопросы 2,3,4,5,7,8.

Спрогнозировать стоимость годового содержания автобуса, который находится в эксплуатации уже пять лет.

Автобус

Расходы на содержание (долл.)

Срок эксплуатации (годы)

Автобус

Расходы на содержание (долл.)

Срок эксплуатации (годы)

Вариант 4. Необходимо составить прогноз объемов продаж книг в мягких обложках за неделю, основываясь на суммарной длине книжных полок в магазине (в ед. изм.). Выборочные данные за 11 недель представлены в табл. 4.11. Используя эти данные, необходимо ответить на вопросы 1 — 5,7,8.

Спрогнозировать количество книг, продаваемых за неделю при суммарной длине книжной полки в магазине, равной 4 ед. изм.

Неделя	Количество проданных книг, Y	Суммарная длина книжных полок (ед. изм.), X
6,8
3,3
4,1
4,2
4,8
3,9
4,9
7,7
3,1
5,9
5,0

Вариант 5. В табл.4.12 приведена информация по 12 различным городам, где продаются товары по почте. Используя данные, ответьте на вопросы 6,7,8. Вычислите стандартную ошибку оценки. Определите, имеется ли значимая линейная взаимосвязь между этими двумя переменными (при уровне значимости 0,05). Какой процент изменчивости переменной количества заказов объясняется переменной количества распространенных каталогов? Проверьте, будет ли угловой коэффициент существенно отличаться от нуля (используйте уровень значимости 0,01). Постройте 90%-ный интервал прогноза для количества полученных заказов, если считать, что было распространено 10 000 каталогов.

Город	Количество заказов на товары (тыс. шт)	Количество распространенных каталогов (тыс. шт)
A
B
C
D
E
F
G
H
I
J
K
L

Вариант 6. В табл. 4.13 приведены размеры банковских вкладов и начисляемых процентов за 10 лет. Используя эти данные, ответьте на вопросы 1,3,7,8.

Размеры вкладов (тыс. усл. ед.)	Средний банковский процент
4,8
5,1
5,9
5,1
4,8
3,8
3,7
4,5
4.9
6,2

Может ли быть найдено эффективное уравнение прогноза? Спрогнозируйте объем вкладов, если банковская ставка будет равна 4%?

Вариант 7. Аналитиком компании выявлена положительная зависимость между общим количеством выданных разрешений на строительство и объемом работ, за которые могла бы взяться его компания. Теперь необходимо выяснить, можно ли использовать информацию о размере банковской учетной ставки для прогнозирования количества разрешений на строительство, выдаваемых за месяц. Соответствующие данные, собранные за девять месяцев, представлены в табл. 4.14. Используя эти данные, ответьте на вопросы 2,5,6,7,8.

Месяц	Количество разрешений на строительство, Y	Банковская учетная ставка, X
10,2
12,6
13,5
9,7
10,8
9.5
10,9
9,2
14,2

На сколько уменьшается в среднем количество разрешений на строительство при возрастании банковской ставки на 1%? Вычислите значение коэффициента детерминации, поясните его.

Вариант 8. На одном из этапов процесса производства электромоторов используется фрезерный станок для изготовления канавок на оси мотора. Каждая партия осей тестируется, и все изделия, размеры которых не соответствуют заданным параметрам, бракуются. Перед изготовлением каждой партии осей фрезерный станок необходимо настроить.

С целью определения оптимального размера партии необходимо выяснить, как размер партии будет влиять на количество бракованных осей. Для этой цели использовать данные о 13 партиях изделий среднего размера, приведенные в табл. 4.15. Используя эти данные, ответьте на вопросы 1,5,7,8. Спрогнозируйте количество бракованных осей для партии размером в 300 изделий.

Партия

Количество бракованных изделий

Размер партии

Партия

Количество бракованных изделий

Размер партии

Вариант 9. В табл. 4.16 представлены данные, собранные при проведении исследований по оценке стоимости недвижимости. Приведенные в таблице величины — это оценка стоимости в городской книге инвентаризации, X, и рыночная цена продажи, Y,(в тыс. усл. ед.) для п = 30 домов, проданных в течение одного года в определенном районе. Используя эти данные, ответьте на вопросы 2,3,7,8.

Дом	Оценка инвентаризации (тыс. усл. ед.)	Рыночная стоимость (тыс. усл. ед.)	Дом	Оценка инвентаризации (тыс. усл. ед.)	Рыночная стоимость (тыс. усл. ед.)
68,2	87,4	74,0	88,4
74,6	88,0	72,8	93,6
64,6	87,2	80,4	92,8
80,2	94,0	74,2	90,6
76,0	94,2	80,0	91,6
78,0	93,6	81,6	92,8
76,0	88,4	75,6	89,0
77,0	92,2	79,4	91,8
75,2	90,4	82,2	98,4
72,4	90,4	67,0	89,8

Продолжение табл. 4. 16

80,0	93,6	72,0	97,2
76,4	91,4	73,6	95,2
70,2	89,6	71,4	88,8
75,8	91,8	81,0	97,4
79,2	94,8	80,6	95,4

Используя модель линейной регрессии, определите прямую регрессионной зависимости рыночной стоимости от цены инвентаризации.

Является ли регрессионная зависимость значимой? Объясните свой ответ. Спрогнозируйте рыночную стоимость дома, цена инвентаризации которого равна 90,5 тыс. долл. Не опасно ли делать такой прогноз?

Тема: Многомерный регрессионный анализ

Лабораторная работа № 5

1. Цель и содержание лабораторной работы.

В простой линейной регрессии рассматривалась взаимосвязь между независимой и зависимой переменными. Связь между двумя переменными часто позволяет точно предсказать значение зависимой переменной, если известно значение независимой переменной. Однако для точного прогнозирования зависимой переменной обычно требуется знать значения более чем одной независимой переменной. Регрессионные модели с несколькими независимыми переменными называются моделями многомерной регрессии.

Выборуравнения многомерной регрессии с наиболее подходящими для прогноза переменными проводится следующим образом:

1. Определение набора возможных независимых переменных.

2. Исключение переменных, не имеющих существенного отно-шения к решению поставленной задачи (если переменная характеризуется значительными ошибками измерения, дублирует другие независимые переменные (мультиколлинеарность), точные данные по ней недоступны);

3. Выбор окончательного вида уравнения с «наилучшими» независимыми переменными, при этом решается задача обеспечения наилучшего прогноза с наименьшими затратами.

Области применения многомерного регрессионного анализа различны:

— отражение взаимосвязи уровня зарплаты работников с географическим расположением компаний, уровнем безработицы в регионе, темпами роста промышленности, членством в союзах, отраслью промышленности или уровнем зарплаты в конкурирующих фирмах;

— анализ изменения цены на акции исходя из получаемых дивидендов, доходов от каждой акции, дробления акций, ожидаемой процентной ставки, объемов сбережений и уровня инфляции;

— исследование влияния на изменение мнения покупателей размеров рекламного бюджета, выбора средств информации, повторения информации, частоты рекламных акций или выбора рекламирующей персоны;

— анализ зависимости объема продаж от расходов на рекламу, уровня цен, маркетинговых расходов конкурентов и разовых заработков покупателей, а также от большого числа других переменных.

Таким образом, целью лабораторной работы является приобретение практических навыков построения уравнения многомерной регрессии предлагаемой социально-экономической ситуации с помощью инструмента анализа данных Excel.

2. Методические положения построения модели многомерной регрессии на основе практического примера.

В табл. 5.1 представлены исходные данные для проведения расчетов, где, Y – выработка продукции, — коэффициент обновления основных фондов, ₂ — доля рабочих высокой квалификации.

Необходимо ответить на следующие вопросы:

1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.

2. Проанализировать линейные коэффициенты парной и частной корреляции.

3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.

Исходные данные для многомерной регрессии

№ предприятия	y	x1	x2	№ предприятия	y	x1	x2
3,9
3,9	6,4
3,7	6,8
7,2
3,8
4,8	8,2
5,4	8,1
4,4	8,5
5,3	9,6
6,8

4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и . Сравнить значения скорректированного и нескорректированного коэффициентов множественной детерминации.

5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после .

6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

Решение с помощью Excel .

1.Дляоценки показателя вариации каждого признака необходимо составить сводную таблицу основных статистических характеристик для одного или нескольких массивов данных, которую можно получить с помощью инструмента анализа данных, Описательная статистика. Для этого следует выполнить следующие шаги:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

в главном меню выберите последовательно пункты Сервис/Анализ данных/Описательная статистика, после чего щелкните по кнопке OK;

2) заполните диалоговое окно ввода данных и параметров вывода (рис. 5.1).

Рис. 5.1. Диалоговое окно ввода параметров инструмента

Входной интервал – диапазон, содержащий анализируемые данные, это может быть одна или несколько строк (столбцов).

Группирование – по столбцам или строкам – необходимо указать дополнительно.

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет.

Выходной интервал – достаточно указать верхнюю левую ячейку будущего диапазона.

Новый рабочий лист — можно задать произвольное имя нового листа.

Если необходимо получить дополнительную информацию по итоговой статистике, уровню надежности, k-го наибольшего и наименьшего значений, установите соответствующие флажки в диалоговом окне. Щелкните по кнопке OK.

Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 5.2.

Рис. 5.2. Результат применения инструмента Описательная статистика

Сравнивая значения средних квадратических σ_y, σ_x1, σ_x21 отклонений и средних величин , и определяя коэффициенты вариации, приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%.

;

;

.

Следовательно, совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2. Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

К сожалению, в ППП Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:

1) в главном меню последовательно выберите пункты Сервис/ Анализ данных/ Корреляция. Щелкните по кнопке OK;

2) заполните диалоговое окно ввода данных и параметров вывода (см. рис. 1.1);

3) результаты вычислений – матрица коэффициентов парной корреляции – представлены на рис. 5.3.

Значения коэффициентов парной корреляции указывают на весьма тесную связь выработки y как с коэффициентом обновления основных фондов — , так и с долей рабочих высокой квалификации — ( и ). Но в то же время, межфакторная связь весьма тесная и превышает тесноту связи с y. В связи с этим для улучшения данной модели можно исключить из нее фактор как малоинформативный, недостаточно статистически надежный.

Рис. 5.3. Матрица коэффициентов парной корреляции

Коэффициенты частной корреляции дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции. Если сравнивать коэффициенты парной и частной корреляции, можно сказать, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи, именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

3. Вычисление параметров линейного уравнения множественной регрессии.

Эта операция проводится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии, а отличие от парной регрессии состоит только в том, что в диалоговом окне при заполнении параметров входной интервал Х следует указывать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены на рис. 5. 4.

Рис. 5.4. Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии вида

;

.

Величина оценивает агрегированное влияние прочих (кроме учтенных в модели факторов и ) факторов на результат y. Величины и указывают, что с увеличением и на единицу результат увеличивается соответственно на 0,9459 и 0,0856 млн. руб. Сравнивать эти значения не следует, т.к. они зависят от единиц измерения каждого признака и потому несопоставимы между собой.

Значения случайных ошибок параметров , и с учетом округления составят: , , . Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Эти значения используются для расчета t-критерия Стьюдента ; ; .

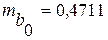
Если значения t — критерия больше 2 — 3, можно сделать вывод о существенности данного параметра, который формируется под воздействием неслучайных причин. Здесь статистически значимыми являются и , а величина сформировалась под воздействием случайных причин, поэтому фактор , силу влияния которого оценивает , можно исключить как несущественно влияющий, неинформативный.

На это же указывает показатель вероятности случайных значений параметров регрессии: если меньше принятого нами уровня (обычно 0,1; 0,05 или 0,01; это соответствует 10%, 5% или 1% вероятности), делают вывод о несущественной природе данного значения параметра, т.е. о том, что он статистически значим и надежен. В противном случае принимается гипотеза о случайной природе значения коэффициентов уровня. Здесь > 5%, что позволяет рассматривать как неинформативный фактор и удалить его для улучшения данного уравнения.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает F-критерий Фишера:

По данным таблицы дисперсионного анализа, представленной на рис. 5.4, =151,65. Вероятность случайно получить такое значение F-критерия составляет 0 (см. значимость F), что не превышает допустимый уровень значимости 5%; об этом свидетельствует величина Р — значение из этой же таблицы. Следовательно, полученное значение неслучайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

Значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации приведены на рис. 5. 4 в рамках регрессионной статистики. Нескорректированный коэффициент множественной детерминации =0,9469 оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации =0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата y в модели факторами и .

5. Информация для оценки с помощью частных F- критериев Фишера целесообразности включения в модель фактора после фактора и фактора после фактора может быть получена в ППП Statgraphics. Частный F- критерий показывает статистическую значимость включения фактора после того, как в нее включен фактор .

Но по данным, вычисленным с помощью ППП Excel, можно сделать общий вывод, который состоит в том, что множественная модель с факторами и с =0,9469 содержит неинформативный фактор . Если исключить фактор

🎥 Видео