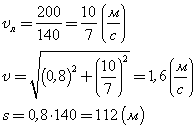Проекция скорости на оси х задана уравнением (3 видео)

Содержание

Зависимость проекции вектора скорости на ось X от времени автомобиля, движущегося прямолинейно, задана уравнением: мх = 10 + 0,5t (м/с)
Ваш ответ
решение вопроса
Похожие вопросы
Как найти проекцию скорости на ось х
10 класс
Материалы к зачету по теме «Основные законы механики «
Проекция скорости на оси х задана уравнением
🎬 Видео

Видео:Построение проекции вектора на осьСкачать

Зависимость проекции вектора скорости на ось X от времени автомобиля, движущегося прямолинейно, задана уравнением: мх = 10 + 0,5t (м/с)

Видео:Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Ваш ответ

Видео:Урок 9. Проекции вектора на координатные осиСкачать

решение вопроса

Видео:ЕГЭ по физике. Задание 1. Определение проекции ускоренияСкачать

Как найти проекцию скорости на ось х

07.06.2019

5 июня Что порешать по физике

30 мая Решения вчерашних ЕГЭ по математике

3.1. Равнопеременное движение по прямой.

3.1.1. Равнопеременное движение по прямой — движение по прямой с постоянным по модулю и направлению ускорением:

3.1.2. Ускорение () — физическая векторная величина, показывающая, на сколько изменится скорость за 1 с.

В векторном виде:

где — начальная скорость тела, — скорость тела в момент времени t.

В проекции на ось Ox:

где — проекция начальной скорости на ось Ox, — проекция скорости тела на ось Ox в момент времени t.

Знаки проекций зависят от направления векторов и оси Ox.

3.1.3. График проекции ускорения от времени.

При равнопеременном движении ускорение постоянно, поэтому будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Значение ускорения: чем дальше от оси времени лежит прямая, тем больше модуль ускорения

3.1.4. Скорость при равнопеременном движении.

В векторном виде:

В проекции на ось Ox:

Для равноускоренного движения:

Для равнозамедленного движения:

3.1.5. График проекции скорости в зависимости от времени.

График проекции скорости от времени — прямая линия.

Направление движения: если график (или часть его) находятся над осью времени, то тело движется в положительном направлении оси Ox.

Значение ускорения: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль ускорения; где — изменение скорости за время

Пересечение с осью времени: если график пересекает ось времени, то до точки пересечения тело тормозило (равнозамедленное движение), а после точки пересечения начало разгоняться в противоположную сторону (равноускоренное движение).

3.1.6. Геометрический смысл площади под графиком в осях

Площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время — это путь, пройденный телом.

На рис. 3.5 нарисован случай равноускоренного движения. Путь в данном случае будет равен площади трапеции:

(3.9)

3.1.7. Формулы для расчета пути

(3.10)

(3.12)

(3.11)

(3.13)

(3.14)

Все формулы, представленные в таблице, работают только при сохранении направления движения, то есть до пересечения прямой с осью времени на графике зависимости проекции скорости от времени.

Если же пересечение произошло, то движение проще разбить на два этапа:

до пересечения (торможение):

После пересечения (разгон, движение в обратную сторону)

В формулах выше — время от начала движения до пересечения с осью времени (время до остановки), — путь, который прошло тело от начала движения до пересечения с осью времени, — время, прошедшее с момента пересечения оси времени до данного момента t, — путь, который прошло тело в обратном направлении за время, прошедшее с момента пересечения оси времени до данного момента t, — модуль вектора перемещения за все время движения, L — путь, пройденный телом за все время движения.

3.1.8. Перемещение за -ую секунду.

За время тело пройдет путь:

Тогда за -ый промежуток тело пройдет путь:

За промежуток можно принимать любой отрезок времени. Чаще всего с.

Если то

Тогда за 1-ую секунду тело проходит путь:

Если внимательно посмотрим, то увидим, что и т. д.

Таким образом, приходим к формуле:

Словами: пути, проходимые телом за последовательные промежутки времени соотносятся между собой как ряд нечетных чисел, и это не зависит от того, с каким ускорением движется тело. Подчеркнем, что это соотношение справедливо при

3.1.9. Уравнение координаты тела при равнопеременном движении

Знаки проекций начальной скорости и ускорения зависят от взаимного расположения соответствующих векторов и оси Ox.

Для решения задач к уравнению необходимо добавлять уравнение изменения проекции скорости на ось:

3.2. Графики кинематических величин при прямолинейном движении

3.3. Свободное падение тела

Под свободным падением подразумевается следующая физическая модель:

1) Падение происходит под действием силы тяжести:

2) Сопротивление воздуха отсутствует (в задачах иногда пишут «сопротивлением воздуха пренебречь»);

3) Все тела, независимо от массы падают с одинаковым ускорением (иногда добавляют — «независимо от формы тела», но мы рассматриваем движение только материальной точки, поэтому форма тела уже не учитывается);

4) Ускорение свободного падения направлено строго вниз и на поверхности Земли равно (в задачах часто принимаем для удобства подсчетов);

3.3.1. Уравнения движения в проекции на ось Oy

В отличии от движения по горизонтальной прямой, когда далеко не всех задач происходит смена направления движения, при свободном падении лучше всего сразу пользоваться уравнениями, записанными в проекциях на ось Oy.

Уравнение координаты тела:

Уравнение проекции скорости:

Как правило, в задачах удобно выбрать ось Oy следующим образом:

Ось Oy направлена вертикально вверх;

Начало координат совпадает с уровнем Земли или самой нижней точкой траектории.

При таком выборе уравнения и перепишутся в следующем виде:

3.4. Движение в плоскости Oxy.

Мы рассмотрели движение тела с ускорением вдоль прямой. Однако этим равнопеременное движение не ограничивается. Например, тело, брошенное под углом к горизонту. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

где A, B и то есть постоянные величины.

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. В математике производная обозначается «’», в физике производная по времени обозначается «∙» над функцией.

то есть скорость является производной от радиус-вектора.

Для проекции скорости:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Таким образом, если известен закон движения то легко можем найти и скорость и ускорение тела.

Теперь воспользуемся понятием интеграла.

то есть, скорость можно найти как интеграл по времени от ускорения.

то есть, радиус-вектор можно найти, взяв интеграл от функции скорости.

Таким образом, если известна функция то легко можем найти и скорость, и закон движения тела.

Константы в формулах определяются из начальных условий — значения и в момент времени

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Треугольник скоростей

В векторном виде при постоянном ускорении закон изменения скорости имеет вид (3.5):

Эта формула означает, что вектор равен векторной сумме векторов и Векторную сумму всегда можно изобразить на рисунке (см. рис.).

В каждой задаче, в зависимости от условий, треугольник скоростей будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

3.6.2. Треугольник перемещений

В векторном виде закон движения при постоянном ускорении имеет вид:

При решении задачи можно выбирать систему отсчета наиболее удобным образом, поэтому не теряя общности, можем выбрать систему отсчета так, что то есть начало системы координат помещаем в точку, где в начальный момент находится тело. Тогда

то есть вектор равен векторной сумме векторов и Изобразим на рисунке (см. рис.).

Как и в предыдущем случае в зависимости от условий треугольник перемещений будет иметь свой вид. Такое представление позволяет использовать при решении геометрические соображения, что часто упрощает решение задачи.

10 класс

Материалы к зачету по теме «Основные законы механики «

1. Механическое движение.
Явление механического движения тел (материальных точек)состоит в том, что положение тела относительно других тел, т. е. его координаты, с течением времени изменяется.Чтобы найти координаты тела в любой момент времени, нужно знать начальные координаты и вектор перемещения тела. Изменение координаты тела равно проекции вектора перемещения на соответствующую ось координат.

Прямолинейное равномерное движение — это самый простой вид движения.При таком движении нужно определять лишь одну координату потому, что координатную ось можно направить вдоль направления движения тела. Координату х тела (материальной точки) в любой момент времени t можно вычислить по формуле:

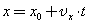
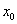
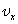
где — начальная координата тела, а — проекция вектора его скорости на ось х. При вычислениях по этой формуле знаки входящих в нее величин определяются условием задачи.

Механическое движение относительно. Это значит, что перемещение и скорость тела относительно различных систем координат, движущихся друг относительно друга, различны.

Покой также относителен. Если относительно какой-то системы координат тело покоится, то существуют и такие системы отсчета, относительно которых оно движется.

2. Основная задача механики
состоит в нахождении положения тела в любой момент времени. Решение этой задачи идет по своеобразной «цепочке»:
чтобы найти координату точки, нужно знать ее перемещение, а чтобы вычислить перемещение, нужно знать скорость движения.
По такой цепочке: скорость → перемещение → координата решают задачи механики для прямолинейного равномерного движения.

Если движение ускоренное, то нужно знать ускорение, так что при таком движении задачи решают по «цепочке» ускорение → скорость → перемещение → координата. И для равномерного, и для ускоренного движения должны быть известны начальные условия — начальные координаты и начальная скорость.
При прямолинейном ускоренном движении мгновенная скорость тела (материальной точки) непрерывно изменяется от одного момента времени к другому. Поэтому для вычисления скорости в любой момент времени и в любой точке нужно знать быстроту ее изменения, т.е. ускорение:

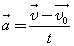
Проекцию скорости тела на выбранную координатную ось в любой момент времени t вычисляют по формуле:

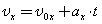
Координату тела находят по формуле:

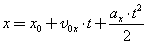
Проекцию перемещения находят по формуле:

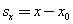
Из приведенных формул получаются формулы для скорости, координат и перемещений при равномерном прямолинейном движении, если принять, что а x = 0.

Значение проекции перемещения при равноускоренном движении можно определить также по формуле:

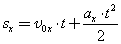
Так как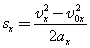

, то для координаты тела х имеем: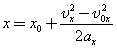

Проекция скорости на оси х задана уравнением

При вычислениях по приведенным формулам знаки проекций векторов 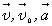, а также знак начальной координаты х, определяются условием задачи и направлением оси координат.

3. При криволинейном движении непрерывно изменяется направление вектора скорости, и в каждой точке траектории он направлен по касательной к траектории в данной точке. Поэтому даже равномерное движение по криволинейной траектории, при котором значение модуля скорости постоянно, есть ускоренное движение. Движение тела (материальной точки) по окружности описывают не только с помощью линейных величин — перемещения и скорости, но и с помощью угловых величин — угла поворота радиуса &#966, проведенного из центра окружности к телу, и угловой скорости ω.

Связь между линейной и угловой скоростью выражается формулой:

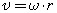
где r — радиус окружности.
При равномерном движении по окружности вектор ускорения в любой точке окружности перпендикулярен вектору скорости и направлен к центру окружности. Модуль вектора центростремительного ускорения выражается равенством:

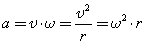
Относительно вращающегося стержня (оси) не закрепленное на нем тело (точка) движется вдоль стержня по направлению от оси вращения.

Пример решения задачи:

1. Ширина реки 200 м. Лодка, держа курс перпендикулярно течению реки, достигла противоположного берега за 140 с. Скорость течения воды в реке 0,8 м/с. Определите скорость и перемещение лодки относительно берега.

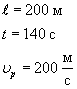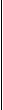Вычисления:

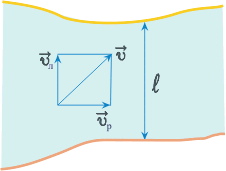
Ответ: Скорость лодки относительно берега 1,6 м/с, перемещение 112 м.

Решите задачи самостоятельно:

1. Через реку переправляется лодка, выдерживая курс перпендикулярно течению. Скорость лодки
4 м/с, скорость течения реки 3 м/с. Какова ширина реки, если лодку снесло на 60 м?

2. 9 км/ч = . м/с; 10 м/с = . км/ч; 8 км/с = . км/ч, 54 км/ч = . м/с.

3. Автомобиль движется: а) с постоянной скоростью; б) с постоянным ускорением;
в) с положительным ускорением; г) с отрицательным ускорением.
Назовите вид каждого движения и изобразите соответствующие графики скорости.

В векторной форме уравнения записываются легко и кратко. Но для практических вычислений нужно знать проекции вектора на оси координат выбранной системы отсчета. Положение точки А (рис. 2.8) задается радиус-вектором г . Спроецируем вектор г на оси х,у, z.

Рис. 2.8. Вектор перемещения точки А и её скорость 1)

Понятно, что х, у₉ z зависят от времени t, т. е. *(/), y(t), z(t). Зная зависимость этих координат от времени (закон движения точки), можно найти в каждый момент времени скорость точки.

Проекции вектора скорости и на оси x,y₉z в обозначениях Лейбница:

Эти три равенства эквивалентны векторному равенству и = —.

Согласно общей формуле (2.2.2) модуль вектора скорости

Так как скорость — величина векторная, то её можно представить с помощью единичных векторов i, j, k :

В произвольном случае движения скорость нс остается постоянной. Быстрота изменения скорости по времени и направлению характеризуется ускорением

Ускорение — величина векторная. При криволинейном движении и изменяется также и по направлению. В какую сторону? С какой скоростью? Выражение (2.3.8) на эти вопросы не отвечает.

Введем единичный вектор т (рис. 2.9), связанный с точкой А и направленный по касательной к траектории движения точки А (векторы т и и в точке А совпадают). Тогда можно записать:

где о = |о| — модуль вектора скорости.

Рис. 2.9. К выводу тангенциальной составляющей ускорение: единичный вектор х направлен по касательной к траектории

Найдем ускорение:

Получаем два слагаемых ускорения: a_х — тангенциальное ускоре-

пие, совпадающее с направлением о в данной точке, а_п — нормальное ускорение, или центростремительное, т. к. направлено оно к центру кривизны, перпендикулярно вектору т .

где do/dt — скорость изменения модуля вектора скорости о.

Итак, a_z показывает изменение вектора скорости по величине:

• если do/d/ > 0, то а_г направлено в ту же сторону, что и вектор о, т. е. ускоренное движение;
• если do/d/ 0), центры кривизны О и О’ сливаются и угол поворота Д d dx d r dx i) 2 r

Tогда — = —, следовательно — = — n ; наконец, и — = — n , т. с.

Нормальное ускорение показывает быстроту изменения направления вектора скорости. Модуль нормального ускорения

Центростремительным называют ускорение, когда движение происходит по окружности. А когда движение происходит по произвольной кривой, говорят, нормальное ускорение, перпендикулярное к касательной в любой точке траектории.

Итак, возвращаясь к выражению (2.3.9), можно записать, что суммарный вектор ускорения при движении точки вдоль плоской кривой равен:

На рис. 2.11 изображено взаимное расположение векторов ускорения:

Рис. 2.11. Суммарное ускорение, нормальная и тангенциальная составляющие ускорения

Как видно из этого рисунка, модуль общего ускорения равен:

Рассмотрим несколько предельных (частных) случаев:

• а_Т = 0; а_п = 0 — равномерное прямолинейное движение;
• а_х = const ;а_п = 0 — равноускоренное прямолинейное движение;
• а_х — 0; а_п = const — равномерное движение по окружности.

Прямая задача кинематики сводится к определению кинематических характеристик по известному закону движения.

При движении с постоянным ускорением (а = const)

Если и = о₀ ± at (а = const), то

Обратная задача кинематики заключается в нахождении закона движения по известной скорости (ускорению) и начальному кинематическому состоянию.

Пусть нам известно ускорение точки в каждый момент времени.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Проекция скорости на оси х задана уравнением

Проекция скорости движения тела, движущегося вдоль оси х, задана уравнением Vх=8-2t.Отметьте,какет из приведенных четырех утверждений правильные,а какие-нет.

нужно каждое утверждение объяснить

А.За первые 2 с движения координата х тела изменилась на 12 м Б

.Координата х тела изменяется по закону:х=8-2t В.

Тело движется равномерно Г.

Через 4 с после начала движения, скорость тела будет равна нулю