Проект по математике 6 класс на тему решение уравнений (3 видео)

«Решение уравнений» Математика 6 класс

Презентация к уроку матемтики на тему: «Решение уравнений»

Содержание

Просмотр содержимого документа «»Решение уравнений» Математика 6 класс»
Решеие уравнений. Проект
Скачать:
Подписи к слайдам:
Предварительный просмотр:
Презентация на тему: «Решение уравнений для 6 класса»
Описание презентации по отдельным слайдам:
🎥 Видео

Просмотр содержимого документа
«»Решение уравнений» Математика 6 класс»

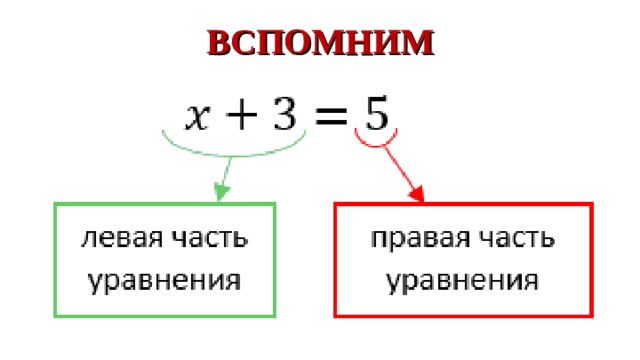
1. Уравнением называют равенство, содержащее букву, значение которой надо найти

2. Корнем уравнения называют то значение неизвестного, при котором это уравнение обращается в верное числовое равенство

3. Решить уравнение — это значит, найти все его корни или убедиться, что это уравнение не имеет ни одного корня

1) Если к обеим частям данного уравнения прибавить (или вычесть ) одно и то же число , то получим уравнение, имеющее те же корни, что и данное

2) Если обе части уравнения умножить (или разделить ) на одно и то же отличное от нуля число , то получим уравнение, имеющее те же корни, что и данное

3) Если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак на противоположный , то получим уравнение, имеющее те же корни, что и данное

Алгоритм решения уравнений

1) у простить уравнение (раскрыть скобки)

2) перенести слагаемые с буквой в левую часть уравнения , без буквы – в правую часть

3) привести подобные слагаемые

4) разделить левую и правую части уравнения на множитель перед буквой

Видео:Решение уравнений. Видеоурок 28. Математика 6 классСкачать

Решеие уравнений. Проект

проект по решению уравнений в 6 классе

Видео:Решение уравнений, 6 классСкачать

Скачать:

Вложение	Размер
reshenie_uravneniy.pptx	846.4 КБ
proekt_reshenie_uravneniy_v_tekstovom_redaktore.doc	356.5 КБ

Предварительный просмотр:

Видео:Решение уравнений - математика 6 классСкачать

Подписи к слайдам:

Муниципальное образовательное учреждение «Красносельская средняя общеобразовательная школа» проект Решение уравнений

«Предмет математики настолько серьёзен, что полезно не упустить случая сделать его немного занимательным». Б. Паскаль «Умственный труд на уроках математики – пробный камень мышления». В.А. Сухомлинский «Лучший способ изучить что-то – это открыть самому». Д. Пойа

Цели и задачи проекта Цель: р азвитие исследовательской компетентности учащихся посредством освоения ими новых знаний, выходящих за рамки школьной программы, по теме «Уравнения». Задачи: — формирование способности творчески, логически мыслить, последовательно рассуждать и представлять конечный результат; — формирование социальной и предметной компетентности; — формирование навыков самостоятельной работы с учебным материалом; — формирование умения работать в команде и навыков общения; — эффективно использовать знания в реальной жизни.

введение Основополагающий вопрос: зачем нужно изучать уравнения ? Математическое образование – это важнейший компонент общего образования и общей культуры современного человека. Всё, что окружает человека в жизни, так или иначе связано с математикой. Решение многих практических задач сводится к решению уравнений.

УРАВНЕНИЕ – ЭТО Равенство переменной с переменной или несколькими переменными. X=Y+3 Равенство, из которого находят неизвестную величину, обозначенную, как правило, буквой латинского алфавита. 4C-28=64 Два выражения, соединенные знаком равенства . 35-2d=923-5d

Виды уравнений ax + b = 0 ax 2 + bx = 0 ax 3 + bx 2 + cx + d = 0 ax 4 + bx 2 + c = 0 ax 4 + bx 3 + cx 2 + bx + a = 0 ax 4 + bx 3 + cx 2 — bx + a = 0 ab 2 x 4 + bx 3 + cx 2 + dx + ad 2 = 0 ax 4 + bx 3 + cx 2 + dx + e = 0 x n – a = 0 x 2 n + bx n + c = 0 a 0 x 2n + a 1 x 2n?1 + a 2 x 2n?2 +…+ a 2 x 2 + a 1 x + a 0 =0 a n x n + a n-1 x n-1 + … + a 1 x + a 0 = 0

РЕШИТЬ УРАВНЕНИЕ Значит найти все значения неизвестных, при которых оно превращается в верное равенство, или установить, что таких значений нет.

ПЛАН РЕШЕНИЯ УРАВНЕНИЯ (х-3) :4=6 Расставь действия. Какое последнее? Какое слово связано с ним? Вырази делимое х -3=6*4 х -3=24 Что будем находить? х=24+3 х=27

КОРЕНЬ УРАВНЕНИЯ – ЭТО числовое значение буквы, которое обращает уравнение в верное равенство. ( 27 -3 ) : 4=6 24 : 4 = 6 6 = 6

Примеры решения уравнений 3х = х + 4 4х – 8 = 6 – 3х 3х – х = 4 4х + 3х = 6 + 8 2х = 4 7х = 14 х = 4 : 2 х = 14 : 7 х = 2 х = 2 х + 3 = х +5 ( х + 3) * 9 = ( х + 5) *9 7х + 27 = 6х + 45 7х – 6х = 45 – 27 Х = 18

Примеры решения уравнений — 40 * (- 7х +5) = — 1600 (- 40 * (- 7х +5 )) : (- 40) = — 1600 : (- 40) — 7х + 5 = 40 — 7х = 40 – 5 — 7х = 35 х = 35 : (- 7) х = — 5

Примеры решения задач при помощи уравнений Что можно снять с каждой чаши, не нарушая равновесия ? Запишите , какое уравнение было первоначально и какое получилось? 5х = 2х + 6 5х – 2х = 2х – 2х + 6 2х = 6 х

х = 2 Ответ: 2 кг масса одного арбуза

Примеры решения задач при помощи уравнений В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько литров молока в каждом бидоне?

Примеры решения задач при помощи уравнений Получим уравнение: 3х – 20 = х + 20

3х — х =20 + 20 2х = 40 Х = 20 20*3 = 60(л) – молока в 1 бидоне. Ответ: 60 л, 20 л.

Задача Диофанта На родном языке: На языке алгебры: Путник! Здесь прах погребен Диофанта. И числа поведать могут, о чудо, сколь долог был век его жизни. х Часть шестую его представляло прекрасное детство. Двенадцатая часть протекла еще жизни – покрылся пухом тогда подбородок. Седьмую в бездетном браке провел Диофант. Прошло пятилетие; он был осчастливлен рождением прекрасного первенца сына. 5 Коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом. И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился. 4 Скажи , сколько лет жизни достигнув, смерть воспринял Диофант?» Уравнение : Х = + + + 5 + + 4 На родном языке: На языке алгебры: Путник! Здесь прах погребен Диофанта. И числа поведать могут, о чудо, сколь долог был век его жизни. х Часть шестую его представляло прекрасное детство. Двенадцатая часть протекла еще жизни – покрылся пухом тогда подбородок. Седьмую в бездетном браке провел Диофант. Прошло пятилетие; он был осчастливлен рождением прекрасного первенца сына. 5 Коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом. И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился. 4 Скажи , сколько лет жизни достигнув, смерть воспринял Диофант?»

ВЫВОДЫ: Обе части уравнения можно делить или умножать на одно и то же число. Любой член уравнения можно перенести из одной части уравнения в другую с противоположным знаком.

Заключение: При работе над проектом мы узнали много нового и полезного из области математики. Познакомились с биографией великих математиков. Узнали о том, где применяется решение уравнений в жизни современного человека.

Великие математики Диофант ( Dióphantos ) (вероятно , 3 в.), древнегреческий математик из Александрии. Сохранилась часть его математического трактата «Арифметика» (6 книг из 13), где даётся решение задач, в большинстве приводящихся к неопределённым уравнениям. Абу Абдаллах Мухаммад ибн Муса аль-Хорезми /783 – 850/ – один из крупнейших ученых Средневековья . Алгебраическая книга аль-Хорезми состоит из двух частей – теоретической ( теория решения линейных и квадратных уравнений, некоторые вопросы геометрии) и практической (применение алгебраических методов в решении хозяйственно-бытовых, торговых и юридических задач – дележ наследства, составление завещаний, раздел имущества, различные сделки, измерение земель, строительство каналов).

Над проектом работали: Джолжанова Айслу 7 класс Танатарова Адима 7 класс Сидоренков Илья 6б класс Шаманов Данил 6б класс Руководитель проекта: Рыжова Наталья Михайловна учитель математики

Источники информации 1. Б.В. Гнеденко «Математика в современном мире». Москва «Просвещение» 1980 г. 2. Я.И. Перельман «Занимательная алгебра». Москва «Наука» 1978 г. 3. Wikipedia. 4. proshkolu.ru.

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Предварительный просмотр:

Муниципальное образовательное учреждение «Красносельская средняя общеобразовательная школа Быковского муниципального района Волгоградской области

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Презентация на тему: «Решение уравнений для 6 класса»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

«Решение уравнений» 6 класс

Устный счёт 1.Раскройте скобки: 4+(a+b+3d) -6+(8,3-3x) 5(4x+3) – 3(x+3) 2.Решите уравнение: 1)6x=-24 3)7x+35=0 2)-40x=80 4)2x=0 3.Найдите значение выражения: 1)-60+12 3)-45+(-34) 2)-70-12 4)160-182 = a+b+3d+4 = 2,3-3x = 17x+6 x=-4 x=-2 x=0 x=-5 = -48 = -82 = -79 = -22

Решение уравнений Уравнение – это равенство, содержащее букву, значение которой надо найти. Чтобы решить уравнение надо найти все его корни или убедиться, что это уравнение не имеет ни одного корня.

Решим уравнение, применив распределительное свойство умножения. 1 Способ 6(x+4)=12 6x+24=12 6x=12-24 6x=-12 x=-12:6 x=-2 Ответ:-2

2 Способ Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель 6(x+4)=12 x+4=12:6 x+4=2 x=2-4 x=-2 Ответ:-2

Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство. Проверка: 6(-2+4)=12 6·2=12 12=12 Ответ: -2

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. 5x+(4x-6)=8x-3 5x+4x-6=8x-3 9x-6=8x-3 9x-8x=-3+6 x=3 Ответ: 3 Пример:

На разминку На разминку становись! Вправо-влево покрутись Повороты посчитай, Раз-два-три, не отставай, Начинаем приседать — Раз-два-три-четыре-пять. Тот, кто делает зарядку, Может нам сплясать вприсядку. А теперь поднимем ручки И опустим их рывком. Будто прыгаем мы с кручи Летним солнечным деньком. А теперь ходьба на месте, Левой-правой, стой раз-два. Мы за парты сядем, вместе Вновь возьмёмся за дела. Физкультминутка

№1319(учебник Виленкин Н.Я.) 0,5x-0,2x=-3 0,3x=-3 x=-3:0,3 x=-10 Ответ: -10. -9n+5n=-33,1-6,9 -4n=-40 n=10 Ответ: 10. -0,4a-0,3a=14 -0,7a=14 a=14:(-0,7) а= -20 Ответ: -20. а) 0,5x+3=0,2x б) -0,4а-14=0,3а г)6,9-9n=-5n-33,1

а) Умножим обе части уравнения на 9. Какой наименьший общий знаменатель у дробей ? (9) №1317 Чтобы избавиться от дробных чисел обе части уравнения умножим на одно и то же число.

Какой наименьший общий знаменатель у дробей ? б) Умножим обе части уравнения на 12 (12)

№1321 В первом бидоне в три раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне? Решение : Ответ: 20л; 60л. А так как, по условию задачи молока в бидонах будет поровну, то составим и решим уравнение: 3x-20=x+20 3x-x=20+20 2x=40 x=40:2 x=20 Значит, во втором бидоне 20 л молока, а в первом бидоне – 60 л. 1 бидон 2 бидон 3x x 3x-20 x+20 было стало

Подведем итоги урока. -Что значит решить уравнение? -Объясните, что такое корень уравнения. -Как проверить, верно ли решено уравнение? -Какое равенство называют уравнением?