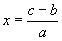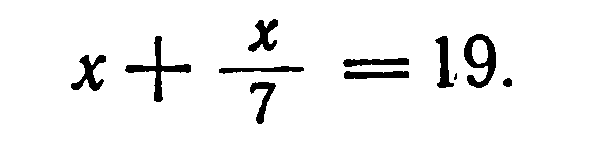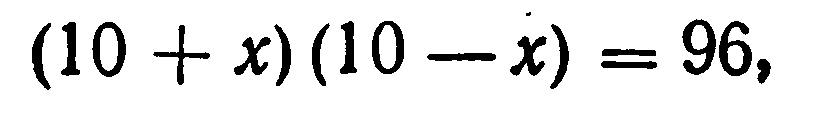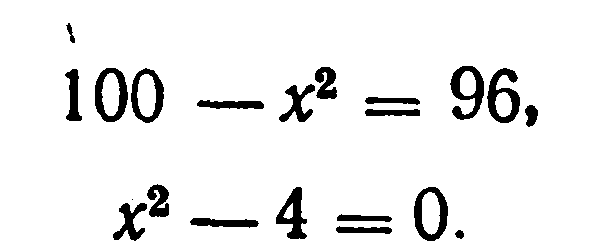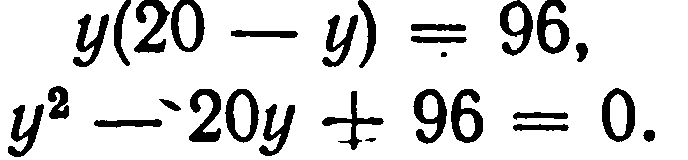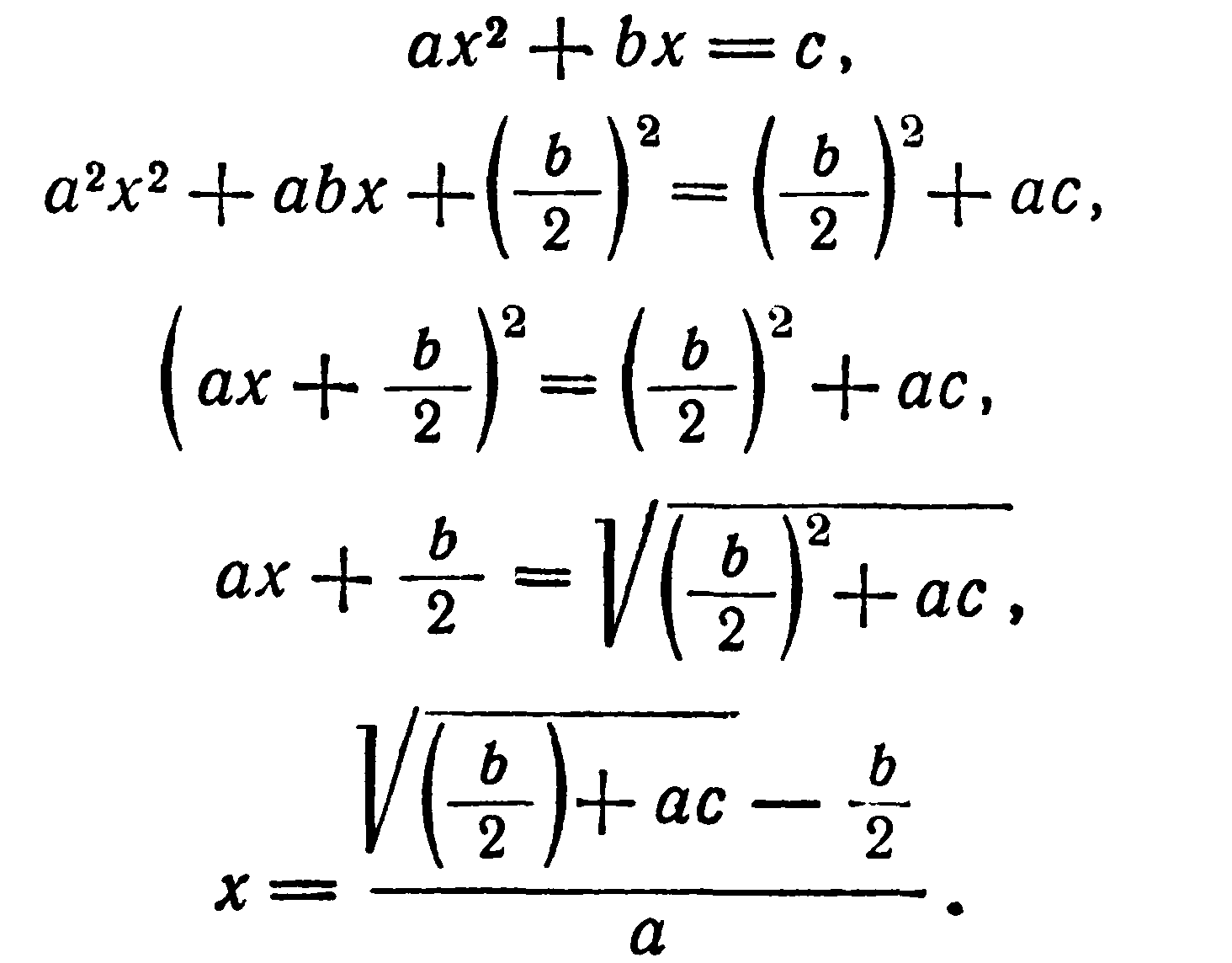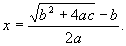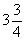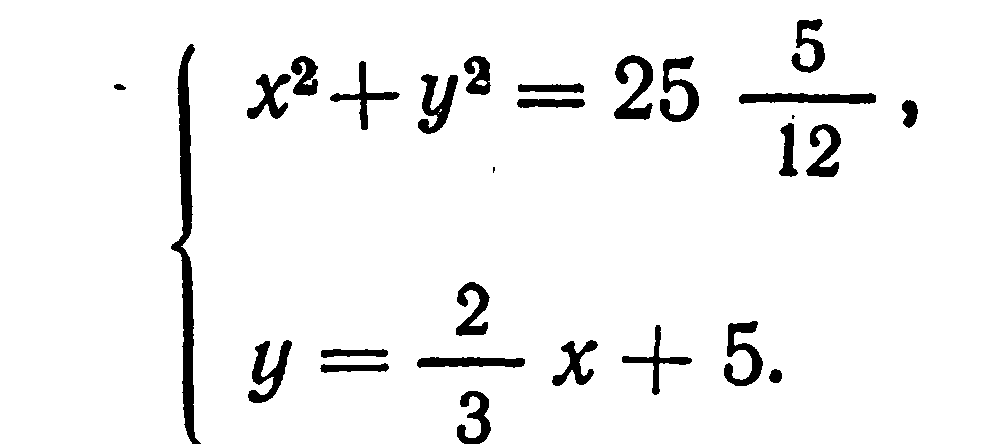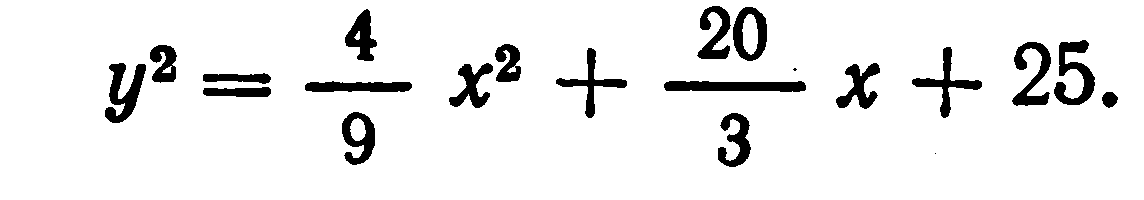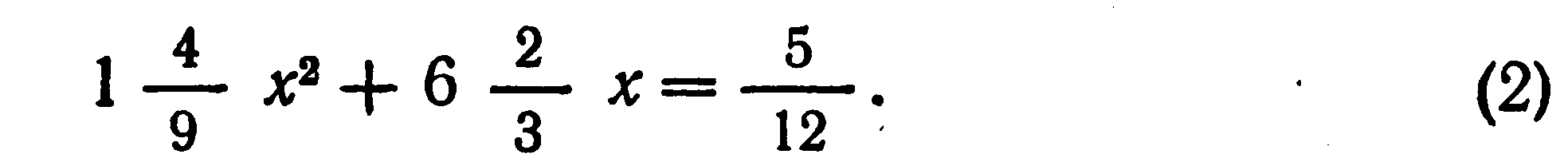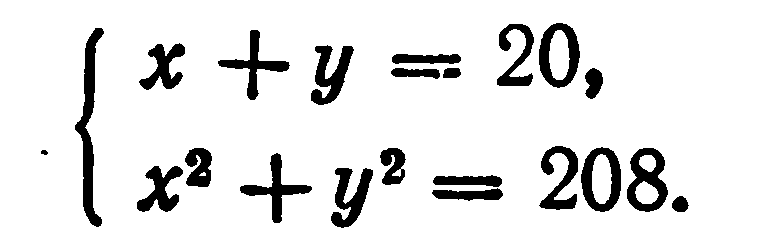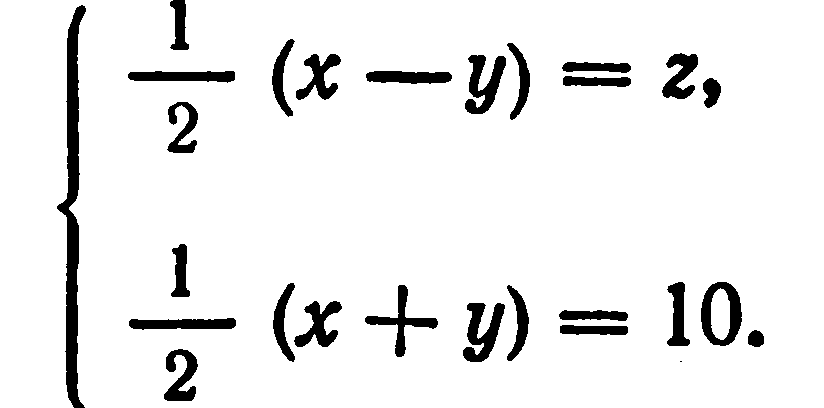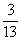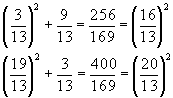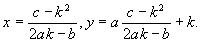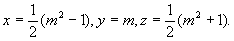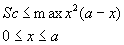Проект на тему методы решения уравнений в странах древнего мира

Видео:Методы решения уравненийСкачать

Методы решения уравнений в странах древнего мира

История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.

В Древнем Египте и Вавилоне использовался метод ложного положения (“фальфивое правило”)

Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь == с, в котором а, Ь, с — целые числа. По правилам арифметических действий ах = с — b,

Если Ь > с, то с — b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).

Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения.

В папирусе Ахмеса 15 задач решается этим методом. Решение первой из них позволяет понять, как рассуждал автор.

Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали “хау” и переводили словом “куча” (“куча” или “неизвестное количество” единиц). Теперь читают немного менее неточно: “ага”.

bqt задача № 24 сборника Ахмеса:

“Куча. Ее седьмая часть (‘подразумевается: “дают в сумме”) 19. Найти кучу”.

Запись задачи нашими знаками:

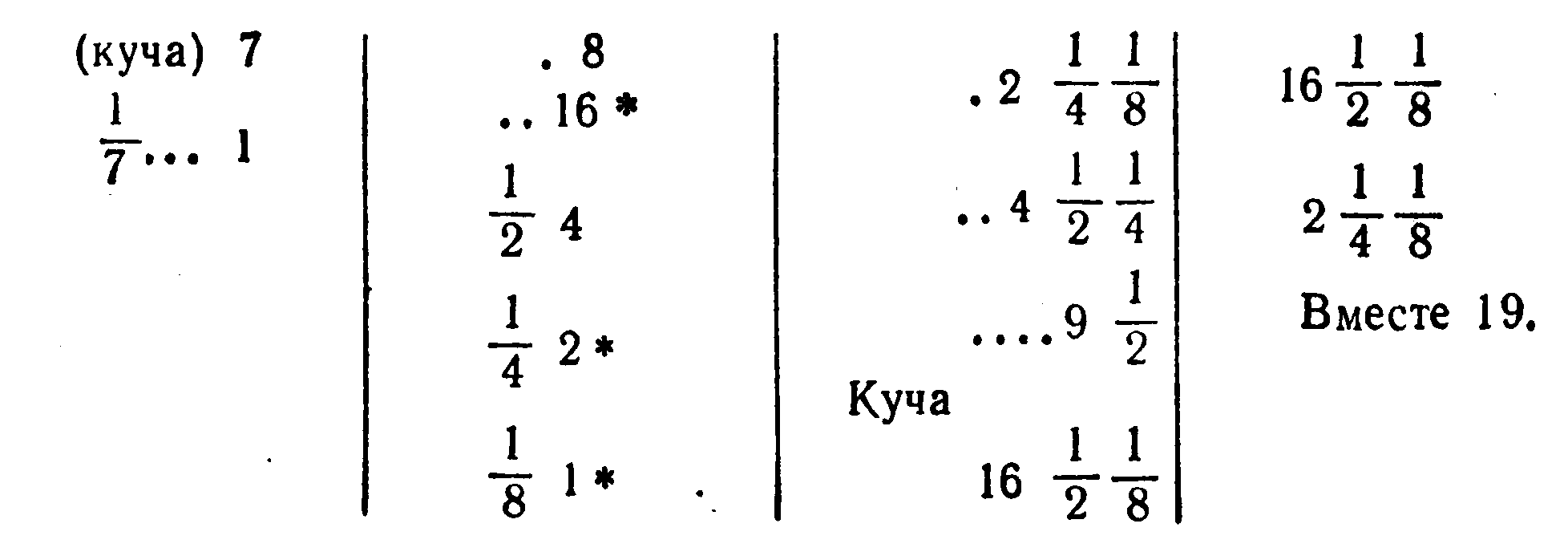
Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:

Во многих задачах в начале или в конце встречаются слова: “Делай как делается”, другими словами: “Делай, как люди делают”.

Смысл решения Ахмеса легко понять.

Делается предположение, что. куча есть 7; тогда 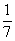ее часть есть 1. Это записано в первом столбце.

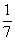
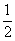
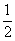
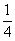
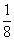
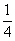
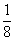
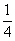
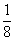
Во втором столбце записано, что при предположении х=7 куча и ее часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит от 8, получает 4. Так как это больше нехватки 3, то на предположение умножить нельзя. Но от 8 есть 2, от восьми 1. Ахмес видит, что и первоначального результата дают точно те 3 единицы, которых не хватало. Отметив и значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на

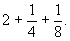
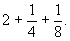
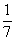
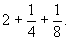
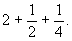
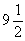
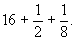
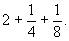
Умножение числа 7 на смешанное число Ахмес заменяет умножением смешанного числа на 7. В третьем столбце выписаны: часть искомой кучи есть , удвоенное это число: и учетверенное: . Сумма этих трех чисел, равная числу , есть произведение первоначального предположения 7 на .

Итак, куча равна .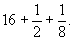

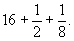
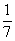
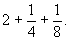
В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи и его части . В сумме получается 19, и решение заканчивается обычным для автора заключением: “Будет хорошо”.

Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах == b. Его применяли как египтяне, так и вавилоняне.

У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получил ту форму, в которой он перешел в учебники европейских народов, в том числе в “Арифметику” Магницкого. Магницкий называет способ решения “фальшивым правилом” и пишет о части своей книги, излагающей этот метод:

Зело бо хитра есть сия часть,

Яко можеши ею все класть (вычислить. — И . Д.)

Не токмо что есть во гражданстве,

Но и высших наук в пространстве,

Яже числятся в сфере неба,

Якоже мудрым есть потреба.

Содержание стихов Магницкого можно вкратце передать так: эта часть арифметики весьма хитрая. При помощи ее можно вычислить не только то, что понадобится в житейской практике, но она решает и вопросы “высшие”, которые встают перед “мудрыми”.

Магницкий пользуется “фальшивым правилом” в форме, какую ему придали арабы, называя его “арифметикой двух ошибок” или “методой весов”.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

. Как составлял и решал Диофант квадратные уравнения ,

В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

“Найти два числа, зная, что их сумма равна 20, а произведение — 96”.

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = —2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения

Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

Квадратные уравнения в Индии.

Задачи на уравнения встречаются уже в астрономическом трактате “Ариабхаттаим”, составленном в 449 г. индийским математиком и астрономом Арибхаттой. Но это уже раннее средневековье.

В Алгебраическом трактате ал-Хорезми даётся классификация линейных и квадратных уравнений.

Индий учёные знали решения неопределённых уравнений в целых числах (в том числе и в отрицательных, чего сам Диофант избегал).

Формула решений квадратного уравнения.

Греческий математик Герон (I или II век нашего летоисчисления) вывел формулу для решения квадратного равнения ax 2 + bx = c умножением всех членов на а и

прибавлением к обеим половинам уравнения :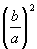

В индии пришли к более простому способу вывода, который встречается в школьных учебниках: они умножали на 4a и к обеим половинам по b 2 . Это даёт:

Индийские математики часто давали задачи в стихах.

Задача о лотосе.

Над озером тихим, с полмеры над водой,

Был виден лотоса цвет.

Он рос одиноко, и ветер волной

Нагнул его в сторону – и уж нет

Цветка над водой.

Нашёл его глаз рыбака

В двух мерах от места, где рос.

Сколько озера здесь вода глубока?

Тебе предложу я вопрос.

Ответ:

Из истории решения системы уравнений, содержащей одно уравнение второй степени и одно линейное

В древневавилонских текстах, написанных в III—II тысячелетиях до н. э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Вот одна из них.

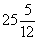
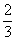
. “Площади двух своих квадратов я сложил: .Сторона второго квадрата равна стороны первого и еще 5”.

Соответствующая система уравнений в современной записи имеет вид:

Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат и согласно формуле квадрата суммы, которая ему, видимо, была известна, получает:

Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:

Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.

Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики”.

Задача 21. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208”.

Эту задачу мы решили бы путем составления системы уравнений:

Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):

Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем

x = 2 + 10; у = 10 —2.

х 2 + у 2 = (г + lO) 2 + (10 — г) 2 == 2z 2 + 200.

z = 2; х = 2 + 10 = 12; у = 10 — 2 = 8.

Задача Диофанта №80 (Из II книги его “Арифметики”)

Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат,

Пусть первое число (I) будет s. Чтобы квадрат его •при прибавлении второго числа дал квадрат, второе число должно быть 2s + 1, так как в таком случае выполняется требование задачи: квадрат первого числа. сложенный со вторым, дает

s 2 + 2s + 1, то есть полный квадрат (s + 1) 2 .

Квадрат второго числа, сложенный с первым, должен также дать квадрат, то есть число (2s + I) 2 + s, равное

4s 2 + 5s + 1 == t 2

Положим, что t = 2s — 2; тогда t 2 = 4s 2 — 8s + 4. Это выражение должно равняться 4s 2 + 5s + 1. Итак, должно быть:

4s 2 — 8s + 4 == 4s 2 + 5s + l откуда s=

Значит, задаче удовлетворяют числа:

.

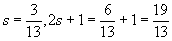
Почему Диофант делает предположение, что t==2s—2, он не объясняет. Во всех своих задачах (в дошедших до нас шести книгах его их 189) он делает то или другое предположение, не давая никакого обоснования.

Вообще содержание 6 книг таково:

В “Арифметике” 189 задач, каждая снабжена одним или несколькими решениями. Задачи ставятся в общем виде, затем берутся конкретные значения входящих в нее величин и даются решения.

Задачи книги I в большинстве определенные. В ней имеются и такие, которые решаются с помощью систем двух уравнений с двумя неизвестными, эквивалентных квадратному уравнению. Для его разрешимости Диофант выдвигает условие, чтобы дискриминант был полным квадратом. Так, задача 30— найти таких два числа, чтобы их разность и произведение были заданными числами,— приводится к системе

Диофант выдвигает “условие формирования”: требуется, чтобы учетверенное произведение чисел, сложенное с квадратом разности их, было квадратом, т. е. 4b + а 2 = с 2 .

В книге II решаются задачи, связанные с неопределенными уравнениями и системами таких уравнений с 2, 3, 4, 5, 6 неизвестными степени не выше второй.

Диофант применяет различные приемы. Пусть необходимо решить неопределенное уравнение второй степени с двумя неизвестными f 2 (х, у) ==0. Если у него есть рациональное решение (x 0 , y 0 ), то Диофант вводит подстановку

в которой k рационально. После этого основное уравнение преобразуется в квадратное относительно t, у которого свободный член f 2 ( x 0 , у 0 ) = 0. Из уравнения получается t 1 == 0 (это значение Диофант отбрасывает), t 2 — рациональное число. Тогда подстановка дает рациональные х и у.

В случае, когда задача приводилась к уравнению у 2 = ax 2 + bx + с, очевидно рациональное решение x 0 = О, y 0 =±C . Подстановка Диофанта выглядит так:

Другим методом при решении задач книги II Диофант пользовался, когда они приводили к уравнению у 2 == = a 2 x 2 + bx + с. Он делал подстановку

после чего х и у выражались рационально через параметр k:

Диофант, по существу, применял теорему, состоящую в том,; что если неопределенное уравнение имеет хотя бы одно рациональное решение, то таких решений будет бесчисленное множество, причем значения х и у могут быть представлены в виде рациональных функций некоторого параметра”

В книге II есть задачи, решаемые с помощью “двойного неравенства”, т. е. системы

Диофант рассматривает случай а = с, но впоследствии пишет, что метод можно применить и при а : с = т 2 , Когда а == с, Диофант почленным вычитанием одного равенства из другого получает и 2 — и 2 = b — d. Затем разность b — d раскладывается на множители b — d = п1 и приравнивает и + v = I, и — v = п, после чего находит

и = (I + п)/2, v = (I — n)/2, х — ( l 2 + п 2 >/4a — <b + d)/2a.

Если задача сводится к системе из двух или трех уравнений второй степени, то Диофант находит такие рациональные выражения неизвестных через одно неизвестное и параметры, при которых все уравнения, кроме одного, обращаются в тождества. Из оставшегося уравнения он выражает основное неизвестное через параметры, а затем находит и другие неизвестные.

Методы, разработанные в книге II, Диофант применяет к более трудным задачам книги III, связанным с системами трех, четырех и большего числа уравнений степени не выше второй. Он, кроме того, до формального решения задач проводит исследования и находит условия, которым должны удовлетворять параметры, чтобы решения существовали.

В книге IV встречаются определенные и неопределенные уравнения третьей и более высоких степеней. Здесь дело обстоит значительно сложнее, потому что, вообще говоря, неизвестные невозможно выразить как рациональные функции одного параметра. Но, как и раньше, если известны одна или две рациональные точки кубической кривой fз (х, у) == 0, то можно найти и другие точки. Диофант при решении задач книги IV применяет новые методы”

Книга V содержит наиболее сложные задачи; некоторые из них решаются с помощью уравнений третьей и четвертой степеней от трех и более неизвестных. Есть и такие, в которых требуется разложить данное целое число на сумму двух, трех или четырех квадратов, причем эти квадраты должны удовлетворить определенным неравенствам.,

При решении задач Диофант дважды рассматривает уравнение Пелля ax 2 + 1 = у 2 .

Задачи книги VI касаются прямоугольных треугольников с рациональными сторонами. К условию х 2 + у 2 == z 2 в них добавляются еще условия относительно площадей, периметров, сторон треугольников.

В книге VI доказывается, что если уравнение ax 2 + b == у 2 имеет хотя бы одно рациональное решение, то их будет бесчисленное множество. Для решения задач книги VI Диофант применяет все употребляемые им способы.

Кстати, в одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраиче-юй загадки, представляющей надгробную надпись на его могиле

Прах Диофанта гробница покоит; дивись ей—и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругою он обручился.

С нею пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

Задача-загадка сводится к составлению и решению уравнения:

откуда х = 84 = вот сколько лет жил Диофант.

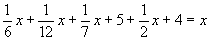
Неопределённое уравнение x 2 + y 2 = z 2

Такое неопределённое уравнение исследовали пиффагорийцы, целые решения которого поэтому называют “пифагоровыми тройками”, они нашли бесконечно много таких троек, имеющих вид:

Более систематическое исследование задач, эквивалентных кубическим уравнениям, относится только к эпохе эллинизма. Архимед в сочинении “О шаре и цилиндре” (книга II, предложение 4) свел задачу о рассечении шара плоскостью на два сегмента, объемы которых имели бы заданное отношение т : п (т > п), к нахождению высоты х большего сегмента из пропорции

(1)

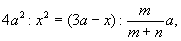
где а — радиус шара.

Архимед обобщает задачу: рассечь заданный отрезок а на две части х и а — х так, чтобы

(а — х) : с = S : х 2 , (2)

где с и S — заданные отрезок и площадь.

Заметив, что при такой общей постановке задача не всегда разрешима (имеются в виду только положительные действительные решения), Архимед приступает к ее исследованию с тем, чтобы наложить ограничения на с и S. Он говорит, что изложит полное решение задачи “в конце”, однако соответствующее место не сохранилось. Жившие на столетие позже Архимеда греческие геометры Диокл и Дионисодор уже не знали его. Они предложили собственные, гораздо более сложные решения, но никто из них не сумел провести анализ общего случая.

Только в VI в. н. э. комментатор Архимеда Евтокий нашел утраченное место. Архимед решает задачу с помощью двух конических сечений:

(3)

(4)

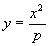
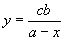
(здесь положено S = pb ). Оба уравнения легко получить из пропорции (2). Для выяснения необходимых условий Архимед переходит от пропорции (2) к кубическому уравнению

которое он выражает словесно как соотношение между объемами. Ясно, что уравнение (5) может иметь положительные корни, если

Итак, проблема сводится к нахождению экстремума х 2 (а — х).

Оставим пока в стороне вопрос о методе экстремумов Архимеда, мы вернемся к этому, когда будем говорить об инфинитезимальных методах древних. Скажем только, что Архимед полностью исследовал условия существования положительных вещественных корней уравнения (5), а именно:

1) если Sc 3 /27, то на участке (0, а) имеются два таких корня;

2) если Sc = 4a з /27, то имеется один корень (как сказали бы мы,— двукратный);

3) если Sc > 4a з /27, то корня нет.

Здесь 4а 3 /27 есть максимум х 2 (а — х) , достигаемый при х = 2а/3 . В конце письма, предпосланного книге “О коноидах и сфероидах” (греки называли сфероидами эллипсоиды вращения, прямоугольными коноидами — параболоиды вращения, а тупоугольными коноидами — полости двуполостных гиперболоидов вращения), Архимед пишет, что с помощью доказанных в книге теорем можно решить ряд задач, как, например: от данного сфероида или коноида отсечь сегмент плоскостью, проведенной параллельно заданной, так, чтобы отсеченный сегмент был равен данному конусу, цилиндру или шару. Перечисленные задачи, так же как и задачи о делении шара, сводятся к кубическим уравнениям, причем в случае тупоугольного коноида уравнение будет иметь вид

Из текста Архимеда можно заключить, что он проанализировал и решил это уравнение. Таким образом, Архимед рассмотрел кубические уравнения вида х 3 + ax + b = 0 при различных значениях a и b и дал метод их решения. Однако исследование кубических уравнений оставалось для греков трудной задачей, с которой, в ее общем виде никто, кроме Архимеда, не мог справиться. Решение отдельных задач, эквивалентных кубическим уравнениям, греческие математики получали с помощью нового геометрического аппарата конических сечений. Этот метод впоследствии восприняли математики стран ислама, которые сделали попытку провести полный анализ всех уравнений третьей степени.

Но еще до этого, и притом греческими математиками, был сделан новый решительный шаг в развитии алгебры: геометрическая оболочка была сброшена, и началось построение буквенной алгебры на основе арифметики. Это произошло в первые века нашей эры.

“История математики в древности” Э. Кольман.

“Решение уравнений в целых числах” Гельфонд.

“В мире уравнений” В.А.Никифоровский.

“История математики в школе” Г.И.Глейзер.

“Рассказы о старой и новой алгебре” И.Депман.

“Пифагор: рассказы о математике” Чистаков.

“Краткий очерк истории математики” Стройк Д.Я.

“Очерки по истории математики” Болгарский Б.В.

“История математики” (энциклопедия) под редакцией Юшкевича.

“Энциклопедический словарь юного математика” под редакцией Гнеденко.

Видео:Методы решения уравненийСкачать

Презентация «Решение уравнений в Древней Индии, Греции, Китае»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Муниципальное бюджетное общеобразовательное учреждение
>

Реферат с элементами самостоятельного поиска
>

Колобова Татьяна Евгеньевна, учащаяся 8 > класса Руководитель: Рыбакова Наталья Александровна

Математика – древний, важный и сложный компонент культуры человека. Она появилась из необходимости практической деятельности человека. Изучая историю математики, мы знакомимся с благородными идеями многих поколений.

Мне приходиться делить время между политикой
и уравнениями. Однако уравнения гораздо важнее.
Политика существует только для данного момента,
а уравнения будут существовать вечно.
А. Эйнштейн

Математика древних греков удивляет в первую очередь богатством своего содержания
Древняя Греция

Диофантовы уравнения
Диофант Александрийский
Математик Древней Греции.
Некоторые называют его «отцом алгебры ».
Создатель «Арифметики», которая
состоит из 13 книг.

Пример: 1) 5x + 35y=40
Решение: Наибольший общий делитель (5, 35) = 5, 40 можно поделить на 5, значит, у этого уравнения есть корни, Например: x=1, y=1

Решение квадратных уравнений с помощью геометрии
x 2
В древние времена, когда геометрия была более изучаема, чем алгебра, математики Древней Греции решали уравнение вот так:
x² + 4x — 21 = 0
x² + 4x = 21, или x² + 4x +4=21+4
Решение: Выражения x² + 4x +4 и 21+4 геометрически представляют тот же самый квадрат, а исходное уравнение x² +4x –21 +4 –4 = 0 – одинаковые уравнения. Получается, что x + 2 = ±5, или х1 = 3 х2 = -7

Творчество математиков Индии значительно повлияло на развитие арифметики, алгебры и тригонометрии
Индийские математики

Математики Индии в отличие от греческих математиков вывели более простую формулу решения квадратных уравнений. Она встречается в школьных учебниках.
Но, не все индийские математики решали именно по этой формуле. Например, Бхаскара решал
квадратные уравнения вот так:
x2 — 44х + 484 = -684 + 1008,
(х — 22)2 = 324,
х — 22= ±18,
x1 = 4, x2 = 40.

Формула корней квадратного уравнения

Магавира при решении систем линейных уравнений использовал метод, который не отличается от метода уравнивания коэффициентов.
Например:
6x -3y =3
5x +4y =22
1) НОК (3;4) =12,
6x -3y =3 *4 24x -12y =12
5x +4y =22 *3 15x +12y =66

2) + 24x -12y =12
15x +12y =66
39x =78 3) 6*2 -3y =3
x= 2 y=3 Ответ: x=2, y=3

Самые заметные научные открытия китайских учёных:
метод численного решения уравнений n -степени (метод Руффини – Горнера);
теоретико-числовые задачи на системы сравнений первой степени с одним неизвестным (сравнения Гаусса);
метод решения систем линейных уравнений (метод Гаусса);
вычисление числа π (пи)

Пример: (y +4)2=y2 +202
Решение китайских учёных
предположительно такое:
(y +4)2=y2 +202 ,
y2+8y+16= y2 +400,
8y=384,
y=48,
Ответ: y=48

В ходе работы я узнала много нового и полезного из области математики. Познакомилась с биографией великих математиков. Узнала, каким методом решали уравнения древнегреческие, индийские и китайские математики. Составила и решила уравнения новыми для меня способами.

Литература
БерезкинаЭ. И. Математика древнего Китая. М.: Наука, 1980
Депман И.Я. История арифметики. — М.: Просвещение, 1965. — 415 с.
Панов В. Ф. Математика древняя и юная/ Под ред. В. С. Зарубина. — 2-е изд. —М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. —648 с.
Рыбников К.А. Возникновение и развитие математической науки. — М.: Изд-во «Просвещение», 1987. — 159 с.
Стройк Д. Я. Краткий очерк истории математики. Пер. с нем.—5- изд., испр.— М.: Наука. Гл. ред. физ.мат. лит., 1990.— 256 с

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 693 человека из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 859 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

• Сейчас обучается 49 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

• Для всех учеников 1-11 классов
  и дошкольников
• Интересные задания
  по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:Математика это не ИсламСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 841 948 материалов в базе

Ищем педагогов в команду «Инфоурок»

Другие материалы

• 15.04.2018
• 982
• 1

• 15.04.2018
• 593
• 7

• 15.04.2018
• 2597
• 58

• 15.04.2018
• 617
• 3

• 15.04.2018
• 394
• 5

• 15.04.2018
• 1038
• 11

• 15.04.2018
• 373
• 1

• 15.04.2018
• 303
• 0

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 15.04.2018 8281
• PPTX 3.8 мбайт
• 73 скачивания
• Рейтинг: 1 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Рыбакова Наталья Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет
• Подписчики: 2
• Всего просмотров: 18737
• Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

Госдума рассматривает проект о регулировании «продленок» в школах

Время чтения: 1 минута

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Эвакуированные в Россию из ДНР и ЛНР дети смогут поступить в вузы по квоте

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Творческие проекты и работы учащихся

В процессе работы над индивидуальным проектом по математике «Различные способы решения квадратных уравнений» учениками 9 класса школы была поставлена и реализована цель, изучить различные методы решения квадратных уравнений.

Подробнее о проекте:

В готовом творческом и исследовательском проекте по математике «Различные способы решения квадратных уравнений» автор выполняет практические задания по решению квадратных уравнений разными способами, подробно описывает их. Также в работе представлен интересный блок из истории развития квадратных уравнений в разных странах и в разные временные отрезки, объясняется теорема Виета. В практической части работы продемонстрированы способы решения квадратных уравнений, некоторые из которых в школе не изучаются.

Оглавление

Введение
1. История развития квадратных уравнений.
2. О теореме Виета.
3. Способы решения квадратных уравнений.
Заключение
Литература
Приложение

Введение

Актуальность. Практически все, что окружает современного человека — это все так или иначе связано с математикой. А достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем решение многих практических задач сводится к решению квадратных уравнений.

В школьном курсе математики мы изучили квадратные уравнения, узнали различные способы решения уравнений второй степени. Этот материал нас заинтересовал, и мы решили узнать, существуют ли другие способы решения квадратных уравнений. Это определило тему нашего исследования: «Квадратные уравнения и методы их решения».

В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Нам пришла идея рассмотреть те способы решения квадратных уравнений, на которые недостаточно времени уделено на уроках или совсем не рассматриваются в школьном курсе.

Вместе с тем, современные научно-методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.

Цель исследования: изучение различных методов решения квадратных уравнений.

• Произвести анализ учебно-методической литературы по решению квадратных уравнений.
• Произвести анализ различных способов решения квадратных уравнений.
• Изучить различные способы решения квадратных уравнений, апробировать их на практике, собрать дидактический материла.

Гипотеза: существуют методы решения квадратных уравнений не изучаемые в школе.

Новизна исследования состоит в комплексном рассмотрении способов решения уравнений второй степени.

Объект исследования: квадратные уравнения.

Предмет исследования: методы решения квадратных уравнений.

Практическая значимость работы состоит в приобретении навыка решения квадратных уравнений различными способами.

Применяемые методы исследования:

1. эмпирические: изучение литературы, обработка материалов.
2. теоретические: сравнение, классификация, анализ, обобщение.

Структура работы: работа состоит из введения, теоретической и практической частей, заключения, списка литературы и приложения.

Видео:Общие методы решения уравнений | Алгебра 11 класс #26 | ИнфоурокСкачать

История развития квадратных уравнений

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Уравнения — это наиболее объёмная тема всего курса математики.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37.», — поучал во II тысячелетии до новой эры египетский писец Ахмес.

В древних математических задачах Междуречья, Индии . [4, c.23], Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри», «Делай так», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) — собрание задач на составление уравнений с систематическим изложением их решений.

Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения с помощью геометрических построений [4, c.21]; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Квадратные уравнения в Древнем Вавилоне

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Как составлял и решал Диофант квадратные уравнения

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.

Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х. Отсюда уравнение: (10 + х)(10 — х) = 96

или же: 100 — х2 = 96, х2 — 4 = 0 (1) Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа. Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения: у(20 — у) = 96,

у2 — 20у + 96 = 0. (2)

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам» [4, c.23], составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а > 0. (1)

В уравнении (1) коэффиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.
Соответствующее задаче 13 уравнение: (x/8)2 + 12 = x.
Бхаскара пишет под видом: х2 — 64х = -768 и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
х2 — 64х + 322 = -768 + 1024,
(х — 32)2 = 256, х — 32 = ± 16, х1 = 16, х2 = 48.

Квадратные уравнения у ал – Хорезми

Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х2 + 21 = 10х).

Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.

Квадратные уравнения в Европе XIII — XVII вв.

Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения.

Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х2 + bx = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

О теореме Виета

Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A — A2, равно BD, то A равно В и равноD».

Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место (а + b)х — х2 = ab, т.е. х2 — (а + b)х + аb = 0,то х1 = а, х2 = b.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. [4, c.25]

Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

🌟 Видео

11 класс, 27 урок, Общие методы решения уравненийСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Уравнения. Методы решения уравненийСкачать

Как решать возвратные уравнения?Скачать

5 способов решения уравнений | Эрик Легион | 100балльный репетиторСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Как решают уравнения в России и США!?Скачать

Как проверяют учеников перед ЕНТСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Алгебра 11 класс (Урок№49 - Уравнения. Методы решения уравнений.)Скачать

№7. МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ + ПРОПОРЦИИ | 7 КЛАСС | УЧЕБНИК Ю. М. КОЛЯГИН И М.В. ТКАЧЕВАСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать