Проект на тему диофантовы уравнения

Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Исследовательская работа по математике по теме: “Диофантовы уравнения, типы и способы решения»

Международная научно-практическая конференция

«Первые шаги в науку»

Исследовательская работа по математике по теме:

“Диофантовы уравнения, типы и способы решения»

Предметная область: математика

Работу выполнила:Хомякова Ольга, ученица 10 класса

Учитель:, учитель математики

МБОУ средняя школа №4 с углубленным изучением отдельных предметов

2.Виды диофантовых уравнений и их классификация

3. Диофантовые уравнения в части С ЕГЭ-13

4. Практическое применение теории диофантовых ур-ний -16

В школьном курсе математики диофантовы уравнения практически не изучаются, но, например, в заданиях группы С6 в ЕГЭ встречаются уравнения 2-ой степени. Также с этими заданиями я сталкивалась в математических олимпиадах. Я заинтересовалась этой темой для того, чтобы успешно сдать Единый Государственный Экзамен и принимать участие в олимпиадах и конкурсах. Помимо этого, меня заинтересовала практическая направленность области этой темы.

Предметная областью моего исследования является математика.

Объект работы — диофантовы уравнения, типы и способы их решения.

1. Повысить уровень математической культуры ;

2. Развить в себе навыки исследовательской деятельности в области математики;

3. Научиться самой и научить других решать диофантовы уравнения эффективными методами;

4. Применять эти методы решения к задачам из повседневной жизни человека, а также к задачам, предлагаемым на вступительных экзаменах в ВУЗы и в олимпиадных заданиях;

5. Классифицировать методы решений дифференциальных уравнений;

6. Составить сборник задач с решениями в помощь ученикам нашей школы.

1. изучить исторические корни ;

2. научиться пользоваться научной литературой, строить графики в современных компьютерных программах, быстро и грамотно находить информацию в интернете;

3. исследовать методы решения задач, приводимых к уравнениям первой степени с двумя переменными, выбрав самые удобные и простые;

4. научиться решать задачи из повседневной жизни, вступительных экзаменов в ВУЗы экономического направления и олимпиадных заданий, применив изученные ранее методы;

5. разработать методическое пособие для всех интересующихся (подобрать или самим составить задачи с экономическим содержанием, приводящие к решению уравнений с двумя переменными).

Методы исследования : анализ, синтез, сравнение, противопоставление, ранжирование, прогнозирование, наблюдение.

Гипотеза: изучив типы, классифицировав диофантовы уравнения по способам решения можно успешно справиться с решением текстовых задач, задач с практическим содержанием и с частью заданий С6 ЕГЭ.

1. Изучение истории появления диофантовых уравнений, основной литературы по этой теме;

2. Изучение способов и методов решения диофантовых уравнений;

3. Попытка их классификации ;

4. Поиск практической значимости данной темы.

Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Основая часть.

Видео:ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Диофантовы уравненияСкачать

1.Историческая справка.

Диофант( вероятно 3 в. н. э. – древнегреческий математик из Александрии)

Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, у которых отыскиваются целые или рациональные решения.

Эти уравнения названы по имени Диофанта ( вероятно 3 в. н. э. – древнегреческий математик из Александрии), изучавшего такие уравнения.

Диофант представляет одну из наиболее трудных загадок в истории науки. Нам неизвестно ни время, когда он жил, ни предшественники, которые работали бы в той же области. Достаточно решить уравнение первой степени с одним неизвестным – и мы узнаем, что Диофант прожил 84 года.

Наиболее загадочным представляется творчество Диофанта. До нас дошло шесть из тринадцати книг, которые были объединены в “Арифметику”, стиль и содержание этих книг резко отличается от классических античных сочинений по теории чисел и алгебры, образцы которых мы знаем по “Началам” Евклида, его “Данным”, леммам из сочинений Архимеда и Аполлония. “Арифметика”, несомненно, явилась результатом многочисленных исследований, которые остались совершенно неизвестными. Число неизвестных диофантовых уравнениях превосходит число уравнений, и поэтому иногда их называют неопределенными.

Диофантовы уравнения впервые обстоятельно исследовались в книге Диофанта “Арифметика”. Такие уравнения имеют некоторые особенности:

1. Они сводятся к уравнениям или системам уравнений с целочисленными коэффициентами.

2. Требуется найти только целые, часто натуральные решения.

2. Определение, виды диофантовых уравнений и способы их решений.

Итак, диофантовым уравнением для целочисленных переменных х 1 , х 2 , …, х n называется уравнение, которое может быть приведено к виду

Где Р — некоторый многочлен от указанных переменных с целыми коэффициентами.

Простейшим диофантовым уравнением является уравнение вида ax + by = c , где a и b – целые взаимно простые числа. Такое диофантово уравнение имеет бесконечное число решений: если x 0 и y 0 – одно решение, то числа x = x 0 + bn и y = y 0 — an ( где n — любое целое число ) также будут решениями, которыми исчерпывается вся совокупность решений.

Виды диофантовых уравнений:

Итак, я предлагаю рассмотреть решение следующего уравнения:

Так как 8 и 9 взаимно простые числа, т. е. наибольший общий делитель 8 и 9 равен 1 то решение существует. Одно из решений найдем подбором:

x 0 =2, y 0 =3. Остальные решения вычисляются по формулам:

x = x 0 + bn

Если наибольший общий делитель d коэффициентов а и b больше 1, а свободный член с не делится на d , то уравнение ах + by = c не имеет решений в целых числах.

А теперь рассмотрим линейное диофантово уравнение, которое не имеет целых решений:

Для доказательства того, что это уравнение не имеет целых решений, необходимо вынести за скобки общий множитель 5, получим 5( x +7 y )=17 . Тогда левая часть уравнения делится на 5, а правая часть на 5 не делится. Значит, уравнение не имеет решений в целых числах.

Любое уравнение ах + by = с , где НОД(а, b ) = 1, имеет хотя бы одно решение в целых числах.

К диофантовому уравнению приводит и такая задача:

На покупку нескольких открыток по 11 рублей и конвертов по 13 рублей потратили всего 61 рубль. Сколько купили открыток?

Давайте обозначим число открыток через х, а число конвертов через y , то задача сводится к уравнению 11 x +13 y =61 . Очевидно, что по условию задачи здесь пригодны лишь целые положительные числа. Методом подбора найдем такие числа. Данное уравнение имеет только одно такое решение: x =2, y =3 .

Еще в Древнем Вавилоне родилась задача о построении прямоугольного треугольника с попарно соизмеримыми сторонами. Соизмеримость сторон означает, что найдется такой масштаб, в котором катеты и гипотенуза будут выражаться натуральными числами x и y , но тогда:

Таким образом, вавилонская задача сводится к задаче построения всех троек натуральных чисел x , y , z удовлетворяющих предыдущему уравнению. Пифагорейцы нашли способ построения всех его решений. Но, возможно, этот способ был найден еще раньше в Вавилоне и Индии. Так или иначе, решения ( x , y , z ) уравнения x ^2+ y ^2= z ^2 принято называть пифагоровыми тройками: x =2 n +1; y =2 n ( n +1) ; z =2 n ^2+2 n +1 , n принадлежит Z . Примеры пифагорейских троек: 3, 4, 5; 6, 8, 10; 5, 12, 13.

Однако эти формулы не дают возможности найти все пифагорейские тройки чисел, имеющие выбранное исходное число. Формулы Пифагора и Платона и их различные модификации дают только частные решения. Приведем еще примеры пифагорейских троек чисел, которые нельзя получить по указанным формулам: 72, 65, 97; 72, 320, 328.

Эти и другие пифагорейские тройки чисел дает вавилонская клинописная табличка, относимая к эпохе гг. до н. э. Метод вавилонян дает возможность найти все пифагорейские тройки, содержащие выбранные исходные числа.

Известный в теории диофантовых уравнений является проблема Ферма ( Пьер Ферма ( ) – французский математик). Эта проблема носит название великой теоремы Ферма.

Она была сформулирована Ферма примерно в 1630 году на полях книги Диофанта “Арифметика”. Общее доказательство получил английский математик Уайлс в 1995 году.

2уравнения второй степени:

Я предлагаю вам решить 4 уравнения:

Итак, попробуем найти решение для первого уравнения:

Так как число 11 имеет делители только 1 и 11, то возможны следующие сочетания сомножителей:

1. x =1,

Тогда x=1, y=10.

Тогда x=11, y= -10

Тогда x= -1, y= -10

Тогда x= -11, y= 10

Ответ запишем в следующем виде: (1;10), (11;-10), (-1;-10), (-11;10).

Задачу №2 я предлагаю решить аналогичным способом, при помощи 4 систем.

1. х=2,

Тогда х=2, у=1/3 (т. е. система не имеет решения в целых числах).

2. х=1,

Тогда х=1, у=-1/3 (т. е. система не имеет решения в целых числах).

Тогда х=-1, у=1/3 (т. е. система не имеет решения в целых числах).

Тогда х=-2, у=-1/3 (т. е. система не имеет решения в целых числах).

Из этих пар чисел видно, что уравнение не имеет решений в целых числах.

Задачу № 3 тоже можно решить при помощи 4 систем. Решив системы, получим следующие пары чисел: ( 0;-1), (0;1), ( y =4/5), ( y = -4/5)

Последние две системы не имеют целых решений, следовательно, ответ: (0;-1),(0;1).

Последнее уравнение не похоже на 3 предыдущих.

Преобразуем заданное уравнение (вынесем за скобки y и вычтем и прибавим число 3):

В результате преобразований получаем уравнение:

Так как число 2 может быть представлено 4 способами в виде произведения целых чисел 2= (-2) * (-1); 2=( -1) * ( -2); 2=1 * 2; 2= 2*1, то возможны четыре системы. Из них получаем четыре пары чисел (1; -2), (2; -3), ( 4;1), (5;0). Ответом этого уравнения будут являться все 4 пары.

Запишем данное уравнение в виде (3 x – y ) * (3 x + y )=14 . Так как число 14 с учетом порядка следования множителей может быть представлено в виде произведения целых чисел следующим образом: 14=( -2) * (-7); 14=( -7) *(-2); 14=( -1) * ; 14= (-14) * (-1); 14= 2 * 7; 14= 7 * 2; 14= 1* 14; 14= 14* 1, то будет 8 случаев.

Решив все 8 систем, мы получаем дробные значения, а значит, что это уравнение не имеет решений в целых числах.

Разложим левую часть заданного уравнения на линейные множители: Уравнение примет вид: (3 x + 2 y )( x + y )=7

Так как 7 число простое, то оно равно произведению двух целых чисел в четырех случаях. Решив все 4 системы, получим пары чисел (-5;4), (5; -4), ( -13;20), ( 13;-20). Эти числа и будут ответом.

x^2 + y^2 – 2x + 4y=-5

В левой части уравнения выделим полный квадрат:

x^2 – 2x + 1 + y^2 + 4y + 4=0

Сумма квадратов равна 0 лишь в одном случае

( x – 1) ^ 2=0 ,

Решив систему, получим, что x = 1, y = -2

x^2 – 6x + y^2 + 6y + 18=0

Докажем, что это уравнение имеет единственное целочисленное решение.

В левой части уравнения выделим полные квадраты :

( x – 3 )^2 + ( y + 3 )^2=0

Данное уравнение имеет решение, когда

x – 3=0,

Теперь я предлагаю рассмотреть графический метод решения диофантовых уравнений.

Алгоритм построения графика уравнения ах + by + с = 0:

1. Придать переменной х конкретное значение х= х1; найти из уравнения ах1 + by + c = 0 соответствующее значение y = y 1.

2. Придать переменной х другое значение х=х2; найти из уравнения ах2 + by + c = 0 соответствующее значение y = y 2.

3. Построить на координатной плоскости х Oy две точки (х1;у1) и (х2;у2).

4. Провести через эти две точки прямую – она и будет графиком уравнения ах + by + с = 0.

Так, например, уравнение 5 x + 7 y =17 можно решить графическим методом, изобразив прямую 5 x + 7 y = 17, и определив на этой прямой точки, обе координаты которых будут в данном случае натуральными числами.

Целые решения: (2 ;1),( 9;-4), ( 16;-9),(-5;6),(-12;11)

Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

3. Диофантовы уравнения в заданиях С5 ЕГЭ.

Необходимо найти все пары (х, у) целых чисел, удовлетворяющих системе неравенств:

x ^2 + y ^2 x – 20 y – 166, (1)

Рассмотрим на координатной плоскости области, которые описываются заданными неравенствами. А затем выберем в них лишь точки с целочисленными координатам х, у.

Получаем два случая:

1) Неравенство (1) путем выделения полных квадратов сводится к условию

Т. е. описывает внутренность круга с центром А(9; -10) и радиусом R 1=√15 .

2) Неравенство (2) сводится к виду

Т. е. описывает внутренность круга с центром В(16; -6) и радиусом R 2=√21 .

Единственной точкой, принадлежащей одновременно двум кругам, будет точка М( 12; -8). Это выясняется подстановкой в систему числовых значений координат всех узлов квадратной сетки, соседних с точкой М.

Найти наименьшее значение суммы тогда в области

Решением данного неравенства является область, ограниченная окружностью радиусом 2 с центром в точке O (1;-2)

Пусть искомое значение , тогда

Угловой коэффициент равен -1, – значение координаты y при x =0.

Треугольник ABC прямоугольный. Чтобы найти c , достаточно найти ординату точки B . Для этого найдем координаты точек A и B . Зная, что точки лежат на прямой с точкой O (1;-2), т. е. на прямой , и на окружности , решим систему

A ( ) C ( ; )

Согласно рисунку ;

B ( ; )

Ответ:

Видео:Диофантовы уравнения x²+xy-y=2Скачать

4.Практическое применение теории диофантовых уравнений.

Неожиданно, лет 20-30 назад, было осознано, что эту чисто абстрактную теорию можно использовать для построения алгоритмов, которые нужны для криптографии, чтобы зашифровывать и безопасно передавать секретные сообщения, а также снимать и класть деньги в банкоматах и т. п. Теория эта оказалась востребована на практике. Яркий пример: в девяностые годы, когда математикам есть было нечего, многие уехали за границу, но многие и остались здесь, и некоторые математики из провинциальных институтов успешно сотрудничали с банками. Банкиры обратились к ним с просьбой помочь в переводе денег из дальних регионов в Москву. В России есть целая Академия криптографии и научно-исследовательские организации, которые используют такие разработки.

Знаменитый мост Золотые Ворота был построен с применением диофантовых уравнений.

Мост Золотые Ворота

Видео:Диофантовы уравнения x+y=xyСкачать

Заключение.

В процессе исследования типов диофантовых уравнений мне удалось их классифицировать по способам решения, выработать алгоритм решения некоторых распространенных видов этих уравнений, научиться решать текстовые задачи, успешно справляться с заданиями части С ЕГЭ, о чем свидетельствует диплом 2 степени на всероссийской дистанционной олимпиаде по математике на сайте «Инфоурок. Ру.»

Данная исследовательская работа дала мне возможность совершенствовать навыки работы с научно-популярной литературой и освоить программы графопостроители.

Говоря о практическом использовании полученных результатов нельзя не вспомнить слова Алексея Николаевича Крылова: «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле».

Видео:Алексей Савватеев "Диофантовы уравнения". Лекции 1-2Скачать

Исследовательская работа по математике «Диафантовы уравнения»

Исследовательская работа по математике «Диафантовы уравнения», выполнена ученицами 8 Д класса МАОУ СОШ № 3 г. Южно-Сахалинска Мачкалян Ангелиной и Авасбековой Айгерим

Научный руководитель — Цой Ю.Е.

Просмотр содержимого документа
«Исследовательская работа по математике «Диафантовы уравнения»»

Муниципальное автономное образовательное учреждение

Средняя общеобразовательная школа №3 имени Героя России Сергея Ромашина

Исследовательская работа по математике
«Линейные диофантовы уравнения»

Выполнили :ученицы 8 Д класса Мачкалян Ангелина,
Авасбекова Айгерим

Научный руководитель :Цой Ю.Е.

Что такое линейное диофантово уравнения? 5

Диофантовы уравнения в олимпиадных задачах 6

Диофантовы уравнения в экономике 7

Применение в истории 10

Диафантовы уравнения в КИМах ЕГЭ 10

Проблема :диофантовы уравнения не изучается в школьной программе,но для решения олимпиадных задач,а также задания уровня С ЕГЭ поэтому необходимо изучить данную тему

Диофантовы уравнения не изучаются в школьном курсе математики, но присутствуют во многих олимпиадных заданиях и в ЕГЭ группы С 6( № 19). Помимо этого они применяются в молекулярной физике и органической химии, системах цифровой подписи и шифрования, в экономике и теории вероятностей.

Цель— узнать что такое линейные диофатовы уравнения, как они решаются, сферы их применения.

Умение решать диофантовы уравнения поможет решать олимпиадные задания, а также подготовиться к решению ряду задач № 19 ЕГЭ.

Изучить литературу, интернет-ресурсы

Узнать, как решаются, когда не имеют решений

Разобрать решение различных задач, в том числе задания №19 ЕГЭ .

Разработать сборник и предложить для решения на дополнительных занятиях по математике.

Что такое линейное диофантово уравнения?

Древнегреческий математик Диофант Александрийский занимался решением отдельных задач, равносильных неопределенным уравнениям (уравнения, содержащие несколько неизвестных), применяя для этого хитроумные, но частные методы. Между тем простой разбор задач Диофанта показывает, что он не только обозначил проблему решения неопределенных уравнений в рациональных числах, но и дал некоторые общие методы их решения.

Диофантовы уравнения – алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях больше числа уравнений.

Рассмотрим простое диофантово уравнение

Найдем частное решение методом подбора х=7, у=2.

Вычтем из уравнения 1) второе равенство, получим

5 и 8 взаимно простые(НОД=1), 5 не делится на 8, следовательно делится (х-7)

Существует более удобный способ подбора частного решения.

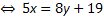
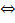
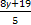
Решаем это уравнение относительно того из неизвестных, при котором наименьший (по модулю) коэффициент. 5х — 8у = 19 х = .

Остатки при делении на 5: 0,1,2,3,4. Подставим вместо у эти числа.

Если у = 0, то х = =.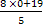

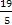
Если у =1, то х = =.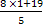

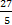
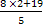
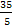
Если у = 2, то х = = = 7 Z.

Если у =3, то х = =.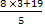

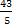
Если у = 4 то х = =.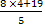

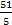
Итак, частным решением является пара (7;2).

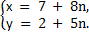
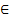
Тогда общее решение: n Z.

Диофантовы уравнения могут и не могут иметь решение.

7(5x+4y) делится на 7, а 25 не делится на 7, т.к. эти части равны, такого быть не может, получили противоречие, значит это уравнение не имеет решений. Мы рассмотрели множество таких уравнений и пришли к выводу, что уравнение вида

ax+by=c, не имеют решение, если a и b делятся на целое число d, а с не делится на d, то диофантовое уравнение не имеет решений.

Диофантовы уравнения в экономике

Задача 1. Как, имея монеты в 5 копеек и в 3 копейки, заплатить кассиру в магазине 13 копеек?

Решение : х— количество монет по 5 коп., у- количество монет по 3 коп. Составим и решим уравнение 5х + 3у= 13. Подберём частное решение х=2, у=1, тогда 5·2+3·1=13,

5х + 3у = 5·2+3·1, перенесём все слагаемые в левую часть и сгруппируем

5·(х-2) + 3·(у-1) =0, обозначим х-2 = х_1, у-1 = у_1, тогда уравнение становиться однородным, 5х₁+3у₁=0, отсюда 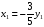, у₁ кратно 5, т.е. у₁ =5n, х₁ = -3n, где n- любое целое число, вернёмся к старым неизвестным х-2= -3n , х= 2-3n,

Ответ: х= 2-3n, у =1+ 5n , где n- любое целое число.

Замечание: Если х будет отрицательным, это значит сдача, т.е. продавец должна будет вернуть .

Задача. 2. Для перевозки зерна имеются мешки, в которые входит либо 60 кг, либо 80 кг зерна. Сколько надо заготовить тех и других мешков для загрузки 1 т зерна таким образом, чтобы все мешки были полными? Какое наименьшее количество мешков при этом может понадобиться?

Решение: Для неизвестных х и у , обозначающих количество мешков по 60 и по 80 кг соответственно, имеем уравнение 60х+80у=1000, сократив обе части уравнения получим 3 х+5 у =50. Надо решить это уравнение в целых неотрицательных числах. Одно целочисленное решение этого уравнения

(-50;50), действительно 3·(-50)+4·50 = 50.

3 х+5 у = 3·(-50)+4·50 , 3( х+50)+5( у-50)=0,

х=4n-50, у=50-3n, где n- любое целое число.

Так как число мешков неотрицательно, то 4n-50 ≥0 и 50-3n ≥0, значит

Видео:Линейные диофантовы уравненияСкачать

Презентация на тему: Диофантовы уравнения

Проблема подтолкнувшая на создание работы: Диофантовы уравнения Глобально не изучаются в школьной программе, а присутствуют на экзамене!

Актуальность моего исследования обусловлена трудностями решения уравнений и задач на составление «Диофантовых уравнений»

Целью моей работы является: -Исследовать варианты решения уравнений с одной неизвестной;-Исследовать варианты уравнений с двумя неизвестными;-Найти общие закономерности результатов решений поставленных задач.

Немного истории… О прожитых годах жизни Диофанта Александрийского можно только предполагать, по написанному стихотворению:Прах Диофанта гробница покоит; дивись ей — и камень.Мудрым искусством его скажет усопшего век.Волей богов шестую часть жизни он прожил ребенком.И половину шестой встретил с пушком на щеках.Только минула седьмая. С подругой он обручился.С нею, пять лет проведя, сына дождался мудрец;Только полжизни отцовской, возлюбленный сын его прожил.Отнят он был у отца ранней могилой своей.Дважды два года родитель оплакивал тяжкое горе,Тут и увидел предел жизни печальной своей.

Мы узнаем годы жизни Диофанта Александрийского.Пусть Диофант прожил x лет. Составим и решим уравнение: Умножим уравнение на 84, чтобы избавиться от дробей:

Арифметика… Основное произведение Диофанта Александрийского– «Арифметика» в тринадцати книгах. К сожалению, до наших дней сохранились только шесть первых книг из тринадцати. «Арифметика» Диофанта – это сборник задач их всего 189, каждая из которых снабжена решением или несколькими способами решения и необходимыми пояснениями. Поэтому, с первого взгляда, кажется, что она не является теоретическим произведением. Однако, при внимательном чтении видно, что задачи тщательно подобраны и служат для иллюстрации вполне определенных, строго продуманных методов.

Диофантовы уравнения с одним неизвестным. Если уравнение с целыми коэффициентами имеет целый корень, то этот корень является делителем числа свободного члена уравнения. Таким образом, при отыскании целых корней уравнения с целыми коэффициентами достаточно испытать лишь делители свободного члена.

Например: Решить в целых числах уравнение:Решение. Свободный член уравнения имеет следующие делители Среди этих чисел и будем искать целые корни данного уравнения. Подстановкой убеждаемся, что корнями являются числа 1 и – 3.

Неопределенные уравнения II-ой степени вида x2 + y2 = z2 Существует еще одна частная задача на неопределенные уравнения – теперь уже второй степени, возникшая примерно за две тысячи лет до Диофанта в Древнем Египте.Если стороны треугольника пропорциональны числам 3, 4 и 5, то этот треугольник – прямоугольный. Этот факт использовали для построения на местности прямых углов. Поступали довольно просто. На веревке на равном расстоянии друг от друга завязывали узлы

В точке С где надо было построить прямой угол, забивали колышек, веревку натягивали в направлении, нужном строителям, забивали колышек в точке В при СВ = 4 и натягивали веревку так, чтобы АС = 3 и АВ = 5. Треугольник с такими длинами сторон называют египетским. Мы, конечно, понимаем, что безошибочность такого построения следует из теоремы, обратной теореме Пифагора. Действительно,32 + 42 = 52 . Говоря иначе, числа 3, 4, 5 – корни уравнения

Запишем подряд квадраты натуральных чисел, а под ними разность между последовательными квадратами: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 … . 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27 … . Найдем в нижнем ряду квадратные числа. Первое из них 32 = 9 , над ним 42 = 16 и 52 =25, знакомая нам тройка 3, 4, 5.Следующее квадратное число в нижней строке 25, ему соответствует 144 и 169, отсюда находим вторую известную нам тройку 5, 12, 13. Отсюда мы имеем право сформулировать такую теорему:

Каждое нечетное число есть разность двух последовательных квадратов

Числа, найденные по такому правилу, всегда будут составлять решение интересующего нас неопределенного уравнения. Это уравнение будем называть «уравнением Пифагора», а его решения – «пифагоровыми тройками». По этому правилу можно получить уже известные нам тройки:

Мои исследования: Заключались в изучении решений задач и уравнений…. И я понял, что для решения задач есть много подходов. Диофант Александрийский не останавливался на одном решении, он находил каждый раз новые и более сложные пути получения результатов.

Куплены фломастеры по 7 рублей и карандаши по 4 рубля за штуку, всего на сумму 53 рубля. Сколько куплено фломастеров и карандашей? Именно эта задача проявила мой интерес к изучению «Диофантовых уравнений» и с неё начались мои исследования!

Решение: Пусть х – число фломастеров, у – число карандашей, тогда по условию 7х+ 4у=53. Частное решение этого линейного диофантова уравнения есть: х=7, у=1. Тогда общее решение его имеет вид: х=7-4t, y=1+7t. Однако условию х> 0, y>0, то значениями параметра t могут быть лишь t=0 и t=1. При t=0 получаем х=7, у=1, а при t=1 имеем: х=3, у=8. Таким образом, решений два, т.е. возможны два варианта покупки фломастеров и карандашей на сумму 53 рубля.

Решить диофантово уравнение: 23х-13у+7z=5 Выбираем наименьший по модулю коэффициенты x,y,z. В нашем случае это 7, затем остальные коэффициенты 23 и 13, при неизвестных представляем в виде: 23= 7*3+2, 13=7*2+(-1), тогда преобразуем уравнение следующим образом: (7*3+2)х-(7*2-1)у+7z=5, Откуда 2х+у+7(3х-2у+z)=5. Полагая теперь t= 3х-2у+z, получаем уравнение: 2х+у+7t=5. Далее находим у из последнего равенства, т.е. у=5-2х-7t и z=-3x+2у+t. Подставляя в последние равенство выражение для у, находим, что z=-3х+2(5-2х-7t)+t=-7х -13t+10. Таким образом, окончательно получаем: У= 5-2х-7t, z=10-7х-13t, где параметры х, и Є Z дают общее решение предположенного диофантова уравнения. Этот метод «наименьшего коэффициента» применим и для решения диофантовых уравнений вида ax+by=c.

Найти все пары натуральных чисел, удовлетворяющих уравнению Разложим левую часть уравнения на множители и запишем уравнение вида: (х-у)(х+у)=69 Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1*69 и 69=3*23. Учитывая, что , получим две системы уравнений, решив которые мы сможем найти искомые числа: или Первая система имеет решение х=35, у=34 , а вторая система имеет решение х=13, у=10. Ответ: (35;34) и (13;10)

В заключительной части своей работы мне особенно хотелось подчеркнуть, что изучив специальную литературу, посвященную диофантовым уравнениям, я расширил свои математические навыки и получил дополнительные знания о самом Диофанте, также о влиянии его научных трудов на дальнейшее развитие научной математической мысли. Именно благодаря методам Диофанта были разгаданы методы самого Архимеда. Методы Диофанта растягиваются еще на несколько сотен лет, переплетаясь с развитием теории алгебраических функций и алгебраической геометрии. Развитие идей Диофанта можно проследить вплоть до работ Анри Пуанкаре и Андре Вейля. Именно Диофант открыл нам мир арифметики и алгебры. Поэтому история Диофантова анализа показалась мне особенно интересной.

Диофантовы уравнения и их решения и по сей день остаются актуальной темой. Умение решать такие уравнения позволяет найти остроумные и сравнительно простые решения казалось бы «неразрешимых» задач, а в практической деятельности значительно сэкономить затраты средств и времени. Проведя данное исследование, я овладел новыми математическими навыками, рассмотрел некоторые методы решения неопределенных уравнений. Изучая диофантовы уравнения, показал практическое им применение, решив несколько задач.

Спасибо за внимание! До скорых встреч. Работу подготовил: Калита Виталий Алексеевич

📽️ Видео

Решение диофантовых уравненийСкачать

Диофантовы уравнения x³-y³=91Скачать

РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать

Решите уравнение в целых числах ★ √x+√y=√50 ★ Как решать диофантовы уравнения?Скачать

Уравнение Диофанта и его приложения | Алексей Савватеев, лекторий НЦФМСкачать

Как решать Диофантовы уравнения ➜ Решите уравнение в целых числах 4x+5y=6Скачать

Нелинейный диофант | Осторожно, спойлер! | Борис Трушин !Скачать

Решите уравнение в целых числах 5x-4y=3 ➜ Как решать Диофантовы уравнения?Скачать

#86. Делимость и диофантовы уравнения! ТРУДНАЯ ЗАДАЧА!Скачать

Диофантовы уравнения 1/x+1/y+1/(xy)=1Скачать

Видеоквант: "Диофантовы уравнения"Скачать