Умение учащихся самостоятельно добывать знания и совершенствовать очень важно, потому что современному обществу, производству нужны работники и руководители, способные быстро и правильно решать постоянно возникающие конкретные задачи, вести диалог с коллегами и партнерами, самостоятельно принимать решения. Поэтому на уроках используются технологии, отвечающие современным требованиям. Одной из таких технологий является “технология проектов”. Суть и идея ее заключается в организации самостоятельной, поисковой, творческой деятельности учащихся.
В основу «технологии проектов» положена идея о направленности учебно-познавательной деятельности школьников на результат, который получается при решении той или иной практической или теоретической значимой проблемы. Внешний результат можно увидеть, осмыслить, применить в реальной практической деятельности. Внутренний результат – опыт деятельности – становится достоянием учащегося, соединяя в себе знания и умения, компетенции и ценности.
- Просмотр содержимого документа «Проект по математике «Способы решения уравнений различных видов»»
- Проектная работа «Виды уравнений и способы их решения» методическая разработка (8 класс) по теме
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- Предварительный просмотр:
- «Виды уравнений и способы их решения»
- Содержимое публикации
- 📸 Видео
Просмотр содержимого документа
«Проект по математике «Способы решения уравнений различных видов»»
Проект по математике
«Способы решения уравнений различных видов»
Подготовили учащиеся 8 класса
Учитель математики — Некрасова Тамара Ивановна
«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».
«Посредством уравнений, теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны»
Тема проекта «Способы решения уравнений различных видов»
Тип проекта: групповой, краткосрочный, творческо-исследовательский
Участники проекта: ученики 8 класса.
Сроки реализации проекта: три недели.
Результат: защита проектов, создание презентации, а затем оказание помощи одноклассникам, испытывающим затруднения по данному учебному материалу.
Целью работы является комплектовать все виды уравнений по видам и разобрать основные способы решения данных уравнений.
Задания для групп (в каждой группе 2 человека)
Зачем нужно уметь решать уравнения?
Какими методами решаются уравнения?
1. Обсуждение и утверждение плана работы. Распределение учащихся на группы, выбор каждой группой вопросов-заданий и форм (проектных продуктов) представления результатов работы (первая неделя).
2. Изучение и анализ источников и литературы.(вторая неделя)
3. Оформление результатов работы над проектом.(вторая неделя)
4. Представление проектных продуктов.(третья неделя)
Работа над проектом
Подбор исторических сведений об уравнениях (1 учащийся)
Задание для группы 1.
Собрать информацию по теме «Линейные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать 10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Задание для группы 2.
Собрать информации по теме «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать 10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Задание для группы 3.
Собрать информации по теме «Дробно-рациональные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).
Подобрать10 – 15 уравнений по данной теме (вместе с решением).
Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).
Подготовиться к защите проекта.
Создание презентации (коллективная работа)
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было нимонет, ни кошельков. Но зато были кучи, а также горшки, корзины, которыепрекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37. «, — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число
павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика»
греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
1) Сейчас мы с вами рассмотрим решения линейных уравнений.
Вспомним, что уравнение вида ax+b=0 называется линейным уравнением или
уравнением первой степени так как при переменной «х» старшая степень
находится в первой степени.
Решение линейного уравнения очень простое:
Пример 1 Решите уравнение 3x+3=5x
Линейное уравнение решается методом переноса членов содержащих
неизвестные в левую часть от знака равенства, свободные коэффициенты в
правую часть от знака равенства:
Значение переменной, обращающее уравнение в верное равенство
называется корнем уравнения.
Выполнив проверку получим:
Значит 1,5 – корень уравнения.
Решения уравнений методом переноса слагаемых из одной части
уравнения в другую, при этом знак слагаемых меняется на противоположный
и применяют свойства уравнений – обе части уравнения можно умножить
(разделить) на одно и то же отличное от нуля число или выражение, можно
рассмотреть при решении следующих уравнений.
Пример 2 Решите уравнения:
а) 6x+1=− 4x; б) 8+7x=9x+4; в) 4(x−8)=− 5
а) Методом переноса решаем
б) Аналогично предыдущему примеру решаем методом переноса:
в) В данном уравнении необходимо раскрыть скобки, применяя
распределительное свойство умножения относительно операции сложения.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Проектная работа «Виды уравнений и способы их решения»
методическая разработка (8 класс) по теме
Проектная деятельность учащихся дает наилучшие результаты в старших классах. Но подготовка к серьезной проектной деятельности начинается еще в 5-8 классах.
Пример проектной работы.
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Скачать:
| Вложение | Размер |
|---|---|
| vidy_urvneniy_i_sposoby_ih_resh.docx | 14.73 КБ |
| lineynye_uravneniya.ppt | 748.5 КБ |
| otchyot_lineynye_uravneniya.doc | 54.5 КБ |
| kvadratnye_uravneniya.ppt | 1.36 МБ |
| kvadratnye_uravneniya_otchet.doc | 47 КБ |
| drobno-ratsionalnye_uravneniya.ppt | 190.5 КБ |
| otchyot_drobno-ratsionalnye_uravneniya.doc | 43.5 КБ |
| uravneniya_vysshih_stepeney.ppt | 1.13 МБ |
| otchyot_uravneniya_vysshih_stepeney.doc | 41.5 КБ |
Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Предварительный просмотр:
Тема проекта : «Виды уравнений и способы их решений».
Участники проекта: ученики 8 класса.
Сроки реализации проекта: две недели.
Результат: защита проектов, а затем оказание помощи одноклассникам, испытывающим затруднения по данному учебному материалу.
Задания для групп (в каждой группе 2-3 человека)
Задание для группы 1.
1.Сбор информации по теме «Линейные уравнения, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).
2.Подбор15-30 уравнений по данной теме (вместе с решением).
3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).
4. Подготовка к защите проекта.
5.Защита проекта (презентация).
Задание для группы 2.
1.Сбор информации по теме «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).
2.Подбор15-30 уравнений по данной теме (вместе с решением).
3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).
4. Подготовка к защите проекта.
5.Защита проекта (презентация).
Задание для группы 3.
1.Сбор информации по теме «Дробно-рациональные уравнения, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).
2.Подбор15-30 уравнений по данной теме (вместе с решением).
3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).
4. Подготовка к защите проекта.
5.Защита проекта (презентация).
Задание для группы 4.
1.Сбор информации по теме «Уравнения высших порядков, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).
2.Подбор15-30 уравнений по данной теме (вместе с решением).
3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).
4. Подготовка к защите проекта.
5.Защита проекта (презентация).
• Приложение 1. «Линейные уравнения, методы их решения»
• Приложение 2. «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения»
• Приложение 3. «Дробно-рациональные уравнения, методы их решения»
• Приложение 4. «Уравнения высших порядков, методы их решения»
Для учеников работа над учебными проектами — это возможность максимального раскрытия их творческого потенциала. Она позволяет проявить себя индивидуально или в группе, попробовать свои силы, приложить свои знания, принести пользу, показать публично достигнутый результат. Это деятельность, направленная на решение интересной проблемы, сформулированной зачастую самими учащимися в виде задачи, когда результат этой деятельности — найденный способ решения проблемы — носит практический характер, имеет важное прикладное значение и, что весьма важно, интересен и значим для самих открывателей.
Предварительный просмотр:
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Подписи к слайдам:
Уравнение вида ax + b = 0 где a , b – некоторые числа, x – переменная, называется линейным уравнением.
Если а ≠ 0 , то линейное уравнение имеет единственный корень х = — b/a Если а = 0 ; b ≠ 0 , то линейное уравнение не имеет решений. Если а = 0 ; b = 0 , то х – любое число.
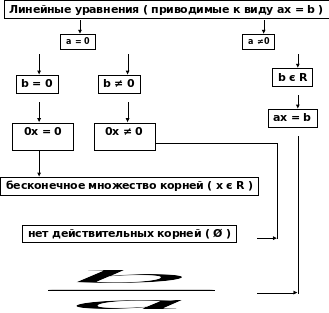
Линейные уравнения (приводимые к виду ax = b ) a = 0 a ≠ 0 b = 0 b ≠ 0 0x = 0 0x ≠ 0 b є R ax = b бесконечное множество корней (x є R) нет действительных корней Один корень ( x = a/b) b = 0 b ≠ 0
Пример 1 . Решим уравнение 2 x – 3 + 4(x – 1) = 5 Решение. 2x – 3 + 4x – 4 = 5 6x = 5 + 4 + 3 6x = 12 x = 12 : 6 x = 2 Ответ : 2
Пример 2. Решим уравнение 2x – 8 – 2(x – 2) = 0 Решение. 2x – 8 – 2x + 4 = 0 — 4 = 0 Ответ : решений нет.
Пример 3. Решим уравнение 3x + 6 – 3(x + 2) = 0 Решение. 3x + 6 – 3x – 6 = 0 0 = 0 Ответ : x – любое число.
Видео:Математика это не ИсламСкачать

Предварительный просмотр:
Уравнение вида ax + b = 0 , где a , b – некоторые числа x – переменная, называется линейным уравнением.
Алгоритм решения линейного уравнения
Если a ≠ 0, то линейное уравнение имеет единственный корень x = —
Пример: 2x – 3 + 4(x -1) = 5
2x – 3 + 4x – 4 = 5
Если a = 0; b ≠ 0, то линейное уравнение не имеет решений.
Пример: 2x – 8 – 2( x – 2 ) = 0
2x – 8 – 2x + 4 = 0
Ответ: решений нет!
Если a = 0; b =0, то x – любое число.
Пример: 3x + 6 – 3( x + 2 ) = 0
3x + 6 – 3x – 6 = 0
Ответ: x – любое число.
Примеры и решения линейных уравнений.
- 6х – 12 = 5х + 4 2 . -9а + 8 = -10а – 2
6х – 5х = 12 + 4 -9а + 10а = -8 — 2
х = 16 : 1 а = -10 : 1
Ответ: 16 Ответ: -10
3. 7m + 1 = 8m + 9 4 . 4 + 25y = 6 + 24y
7m – 8m = 9 – 1 25y – 24y = 6 — 4
m = 8 : (-1) y = 2 : 1
Ответ: -8 Ответ: 2
5. 11 – 5z = 12 – 6z 6. 4k + 7 = -3 + 5k
-5z + 6z = 12 – 11 4k – 5k = -3 — 7
z = 1: 1 k = -10 : (-1)
Ответ: 1 Ответ: 10
7. -40 * ( -7x + 5 ) = -1600 8. ( -20x – 50 ) * 2 = 100
280x – 200 = -1600 -40 – 100 = 100
280x = -1600 + 200 -40 = 100 + 100
280x = -1400 40x = 200
x = -1400 : 280 x = 200 : 40
Ответ: -5 Ответ: 5
9. 2.1 * ( 4 – 6y ) = -42 10. -3 * ( 2 – 15x ) = -6
8.4 – 12.6y = -42 -6 + 45x = -6
-12.6 = -42 – 8.4 45x = -6 + 6
-12.6 = -50.4 45x = 0
y = -50.4 : ( -12.6 ) x = 0 : 45
Ответ: 4 Ответ: 0
11. 13 – 5x = 8 – 2x 12. 5x + ( 3x – 7 ) = 9
-5x + 2x = 8 – 13 5x + 3x – 7 = 9
x = -5 : ( -3 ) x = 16 : 8
Ответ: 1, 2/3 Ответ: 2
13. 4y + 15 = 6y + 17 14. 3y – (5 – y) = 11
4y – 6y = 17 – 15 3y – 5 + y = 11
y = 2 : ( -2 ) y = 16 : 4
Ответ: -1 Ответ: 4
15. -27x + 220 = 5x 16. -2x + 16 = 5x — 19
-27x + 5x = — 220 -2x – 5x = -19 — 16
-22x = -220 -7x = -35
x = -220 : ( -22 ) x = -35 : ( -7 )
Ответ: -10 Ответ: 5
17. 25 – 3b = 9 – 5b
18. 3 * (4x – 8 ) = 3x – 6
19. -4 * ( -z + 7) = z + 17
20. c -32 = ( c + 8 ) * ( -7 )
21. 12 – 2 * ( k + 3 ) = 26
22. -5 * ( 3a + 1 ) – 11 = -16
23. -5 * ( 0.8z – 1.2 ) = -z + 7.2
24. -20 * ( x – 13 ) = -220
25. ( 30 – 7x ) * 8 = 352
26. ( 2.8 – 0.1x ) * 3.7 = 7.4
27. ( 3x – 1.2 ) * 7 = 10.5
28. 6x + 12 – 42x = 0
29. 3( y – 5 ) – 2( y – 4 ) = 8
3y – 15 – 2y – 8 = 8
3y – 2y = 8 + 8 + 15
30. -5( 5 – x ) – 4x = 18
Предварительный просмотр:
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Подписи к слайдам:
Определение 1. Квадратным уравнением называют уравнение вида ax 2 + bx + c =0 , где коэффициенты a , b , c — любые действительные числа, причем а≠0. Многочлен ax 2 + bx + c называют квадратным трехчленом.
Определение 2. Корнем квадратного уравнения ax 2 + bx + c =0 называют всякое значение переменной x , при котором квадратный трехчлен ax 2 + bx + c обращается в нуль; такое значение переменной x называют также корнем квадратного трехчлена. Квадратные уравнения с коэффициентами a , b , c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта. Решить квадратное уравнение –значит найти все его корни или установить ,что корней нет.
Определение 3. Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля. Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один коэффициентов b , c равен нулю. Приведенное квадратное уравнение – это квадратное уравнение, в котором а=1.
Определение 4. Для приведенного квадратного уравнения x 2 + px + q =0 сумма корней равна — p , а произведение корней равно q .
Особые квадратные уравнения: 2 x 2 — x -1= 0 D=9 x 1 =1 x 2 =-1 ∕2 2x 2 +3x-5=0 D=49 x 1 =1 x 2 =-5∕2 x 2 +3x-4=0 D=25 x 1 =1 x 2 = -4
3x 2 +2x-1=0 D=16 x 1 = -1 x 2 = 1/3 2x 2 +x-1=0 D=9 x 1 =-1 x 2 =1/2 x 2 -3x-4=0 D=25 x 1 =-1 x 2 =4
Видео:Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Предварительный просмотр:
Определение 1. Квадратным уравнением называют уравнение вида ax 2 +bx+c=0, где коэффициенты a,b,c- любые действительные числа, причем а≠ 0.
Многочлен ax 2 +bx+c называют квадратным трехчленом.
Определение 2. Корнем квадратного уравнения ax 2 +bx+c=0 называют всякое значение переменной x, при котором квадратный трехчлен ax 2 +bx+c обращается в нуль; такое значение переменной x называют также корнем квадратного трехчлена.
Квадратные уравнения с коэффициентами a, b, c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта.
Решить квадратное уравнение – значит найти все его корни или установить ,что корней нет.
Определение 3. Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля. Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один коэффициентов b,c равен нулю. Приведенное квадратное уравнение – это квадратное уравнение, в котором а=1.
Определение 4. Для приведенного квадратного уравнения x 2 +px+q=0 сумма корней равна
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

«Виды уравнений и способы их решения»
Содержимое публикации
Актуальность темы: Большинство жизненных задач сводится к решению различных видов уравнений. Исходя из этого я хочу помочь систематизировать знания для студентов и сделать картотеку с решением различных уравнений.
Цель проекта: изучить различные виды уравнений и понять способы их решения
1. Изучить литературу и интернет-ресурсы по данному вопросу.
2. Выбрать и разобрать более распространенные виды уравнений.
3. Создать картотеку с решением различных видов уравнений.
Математические уравнения, их виды, способы их решения.
Изучение, анализ, практическое применение полученных знаний.
Практическая значимость проекта:
1. Мой продукт будет полезен для учеников и студентов при подготовке к экзаменам;
2. Привлечения внимания студентов к математике, повышение их заинтересованность в данном предмете и успеваемость.
Глава 1. Теоретические основы применения математических уравнений, их виды и способы решения
Математика — удивительнейшая наука, без которой не может существовать человечество. В ней интересно абсолютно всё — от арифметических действий и решения различных задач до её истории.
Но историей люди зачастую пренебрегают, ссылаясь на то, что математика и история — науки совершенно противоположные. Позвольте разрушить этот стереотип, доказав, что изучать историю очень интересно и, к тому же, важно для знания и понимания самой математики, царицы всех наук.
Представители различных цивилизаций: Древнего Египта, Древнего Вавилона, Древней Греции, Древней Индии, Древнего Китая, Средневекового Востока, Европы овладели приемами решения квадратных уравнений.
Впервые квадратное уравнение сумели решить математики Древнего Египта. В одном из математических папирусов содержится задача:
«Найти стороны поля, имеющего форму прямоугольника, если его площадь 12, а – длины равны ширине». «Длина поля равна 4», – указано в папирусе.
Прошли тысячелетия, в алгебру вошли отрицательные числа. Решая уравнение х²= 16, мы получаем два числа: 4, –4.
Разумеется, в задаче египтян мы приняли бы X = 4, так как длина поля может быть только положительной величиной.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Правило решения квадратных уравнений, изложенное в вавилонских текстах, совпадает, по существу, с современным, однако неизвестно, каким образом вавилоняне «дошли до этого». Но почти во всех найденных папирусах и клинописных текстах приводятся только задачи с решениями. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел!».
Греческий математик Диофант составлял и решал квадратные уравнения. В его «Арифметике» нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
Задачи на составление квадратных уравнений встречаются уже в астрономическом трактате «Ариа-бхатиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой.
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m и др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение, которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5,y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру,x+7=38, z−4=2, 8·t=4, 6:x=3.
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19,x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3,7·x+0,6=1 является уравнением с одной переменнойx, а x−z=5 – уравнением с двумя переменными x и z. Примером уравнения с тремя переменными может быть выражение x2+(y−6)2+(z+0,6)2=26.
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a+1=5 мы заменим букву числом 2, то равенство станет неверным, а если 4, то получится верное равенство 4+1=5.
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0·x=5. Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0.
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x−2=4 есть только один корень – шесть, в x2=9 два корня – три и минус три, вx·(x−1)·(x−2) =0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x+y=7, которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4, то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как(3,4).
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Глава 2 Картотека математических уравнений
2.1. Линейное уравнение
Линейнымуравнением называется уравнение вида ax+b=0, в котором a и b — действительные числа.
Решение линейного уравнения в зависимости от параметра
1. Если a не является 0, у уравнения — один корень.
Например, если 2x−4=0, то x=2.
2. Если a=0, но b не равно 0, у уравнения нет корней.
Например, 0x=3 — нет такого значения x, при умножении которого на 0 можно получить 3.
3. Если a=0 и b=0, то корень уравнения — любое число.
Например, 0x=0 — умножив ноль на любое число, получим 0.
2.2. Степенное уравнение
В показательных уравнениях, которые часто называют степенными, в основании находятся исключительно числа. Переменная же есть только в показателе.
Показательное уравнение — это уравнение, в котором неизвестная величина находится в показателе степени.
Для решения необходимо опираться на следующие свойства и правила:
1. Любое положительное число, возведенное в степень, равную единице, равно самому себе, то есть 91 = 9. Если же возвести число в степень ноль, то результат всегда будет одинаковым, а именно, равным единице: 90 = 1. 2. Если математическое выражение возводится в отрицательное значение, то его можно заменить дробью, где числитель – единица, а знаменатель первоначальное выражение, но уже в положительной степени. Числитель – значение, находящееся над чертой, знаменатель – под ней. Математически правило записывается в следующем виде:
3. Чтобы возвести число в степень, нужно умножить его на себя такое количество раз, которое равно ее значению, то есть р5 = р·р·р·р·р.
4. Если нужно умножить два положительных числа, отличных от единицы и равных между собой, то нужно сложить их показатели и возвести в полученное значение основание: p5·p3= p5+3 = p8.
5. Когда требуется разделить одно число на другое, имеющие отличные показатели, нужно вычесть из одного другой и возвести в полученное значение неизменное основание: p9/p3= p9-3 = p6.
6. Если необходимо возвести одну степень в другую, то нужно их перемножить. Само основание при этом остается без изменений. Его нужно возвести в полученное после арифметических действий значение: (p3)4 = p3*4 = p12.
Применение свойств и правил помогает упростить выражения, быстрее произвести вычисления и получить результат. Закрепить материал помогут подробные объяснения при решении показательных уравнений. Разъяснения на практике помогут изучить сложные моменты и облегчат усвоение знаний.
Упростить и решить уравнение:
В обеих частях примера одинаковые основания, значит, можно приравнять математические выражения, находящиеся в показателе. В результате получится:
Путем переноса чисел в одну часть, а переменных в другую, не сложно решить пример. Главное, не забывать менять знак на противоположный, плюс на минус и наоборот:
2.3. Дробное уравнение
Дробные рациональные уравнения — вид: Рациональное уравнение — это такой вид уравнения в которой левая и правая части рациональные выражения. В записи уравнения имеются только сложение, вычитание, умножение, деление, а также возведение в целую степень. Любое рациональное уравнение сводится к алгебраическому
Например, вот такое уравнение:
В общем виде дробно-рациональные уравнения решают по следующей схеме:
1) Все слагаемые переносим в одну сторону.
2) Дроби приводим к НОЗ (наименьшему общему знаменателю).
3) После упрощения решаем уравнение типа « дробь равна нулю ».
В частных случаях дробно-рациональные уравнения могут быть решены с помощью замены переменной либо разложением на множители.
Начнем с рассмотрения примеров общего случая.
Решить дробно-рациональные уравнения:
Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:
Пришли к уравнению типа «дробь равна нулю» Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Находим значения переменной, при которых знаменатель обращается в нуль, и исключаем их из области допустимых значений:
Теперь находим значения переменных, при которых числитель обращается в нуль:
Это — квадратное уравнение. Его корни
Оба корня удовлетворяют условиям x≠2, x≠ -4. Ответ: 5; -6.
Переносим все слагаемые в одну сторону и приводим дроби к наименьшему общему знаменателю:
— при этих значениях переменной знаменатель обращается в нуль, поэтому их исключаем из ОДЗ.
Из двух корней квадратного уравнения
— второй не входит в ОДЗ. Поэтому в ответ включаем лишь первый корень.
2.4. Иррациональное уравнение
Иррациональными называются уравнения, в которых переменная содержится под знаком корня.
Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства.
Из двух систем выбирают ту, которая решается проще.
Если а 1 не имеет решений.
При|a|≤1 имеет бесконечное число решений.
2. Уравнение cosx=a
При|a|>1 — как и в случае с синусом, решений среди действительных чисел не имеет.
При|a|≤1 имеет бесконечное множество решений.
3. Уравнение tgx=a
Имеет бесконечное множество решений при любых значениях aa.
4. Уравнение ctgx=actgx=a
Также имеет бесконечное множество решений при любых значениях aa
Проанализировав собранную информацию о линейном, степенном, дробном, иррациональном и тригонометрическом уравнениях, все данные я соберу в самодельную картотеку. В ней будут находится данные виды уравнений и способы их решения с примерами. Эта картотека будет выступать продуктом в моей работе.
После сбора информации, я подготовила необходимые материалы для создания продукта. (Приложение А)
Затем сделала фон будущих страниц картотеки. (Приложение Б)
После того как страницы высохли, я перенесла нужную информацию, отталкиваясь на содержание картотеки. (Приложение В)
Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XXI век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
Работа была выполнена в соответствии с поставленными задачами. Я изучила литературу и интернет-ресурсы по своей теме. Из всех видов уравнений я выбрала наиболее распространенные и создала картотеку с их решением.
В ходе работы, пока я создавала свою картотеку, я разобралась в решении уравнений таких видов как: линейное, степенное, дробное, иррациональное и тригонометрическое уравнение. Я надеюсь, что мой доклад может послужить неплохим справочным материалом при решении тех или иных уравнений.
Также мой продукт поможет студентам и школьникам при подготовке к экзаменам. Ведь, видя перед собой наглядный пример уравнений с их решением и примерами, понимать и запоминать информацию намного легче.
Список использованных источников
Аксенова М.Д. Энциклопедия для детей. Том 11. Математика. – М.: Аванта+, 1998. – 688 с.
Бурцева У. А. Системы линейных уравнений. — Волгоград: гос. техн. ун-т. — 2005. — 23 с.
Виленкин Н.Я. «Алгебра для 8 класса», М.: Просвещение, 2000.
Калягин Ю.М., Оганесян В.А. Методика преподавания математики в средней школе. Общая методика. Учебное пособие для студентов физико-математических педагогических институтов. М.: Просвещение, 1985 г. — 462 с.
Фридман Л.М., Е.Н. Турецкий Как научиться решать задачи. Книга для учащихся старших классов средней школы. Москва «Просвещение», 1998 г. — 192 с.
Цыпкин А. Г. Под ред. С. А. Степанова. Справочник по математике для средней школы. – М.: Наука, 1980.- 400 с.
📸 Видео
Решение биквадратных уравнений. 8 класс.Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Как решать дробно-рациональные уравнения? | МатематикаСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение систем уравнений методом подстановкиСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Показательные уравнения. 11 класс.Скачать