Проект линейные уравнения методы их решения

Видео:Решение систем уравнений методом подстановкиСкачать

Проектная работа «Виды уравнений и способы их решения»
методическая разработка (8 класс) по теме

Проектная деятельность учащихся дает наилучшие результаты в старших классах. Но подготовка к серьезной проектной деятельности начинается еще в 5-8 классах.

Пример проектной работы.

Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Скачать:

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Предварительный просмотр:

Тема проекта : «Виды уравнений и способы их решений».

Участники проекта: ученики 8 класса.

Сроки реализации проекта: две недели.

Результат: защита проектов, а затем оказание помощи одноклассникам, испытывающим затруднения по данному учебному материалу.

Задания для групп (в каждой группе 2-3 человека)

Задание для группы 1.

1.Сбор информации по теме «Линейные уравнения, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).

2.Подбор15-30 уравнений по данной теме (вместе с решением).

3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).

4. Подготовка к защите проекта.

5.Защита проекта (презентация).

Задание для группы 2.

1.Сбор информации по теме «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).

2.Подбор15-30 уравнений по данной теме (вместе с решением).

3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).

4. Подготовка к защите проекта.

5.Защита проекта (презентация).

Задание для группы 3.

1.Сбор информации по теме «Дробно-рациональные уравнения, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).

2.Подбор15-30 уравнений по данной теме (вместе с решением).

3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).

4. Подготовка к защите проекта.

5.Защита проекта (презентация).

Задание для группы 4.

1.Сбор информации по теме «Уравнения высших порядков, методы их решения» (использование материалов учебников алгебры 7-8, справочников, Интернета).

2.Подбор15-30 уравнений по данной теме (вместе с решением).

3.Оформление отчёта о проделанной работе: теория + практические задания («бумажный» вариант).

4. Подготовка к защите проекта.

5.Защита проекта (презентация).

• Приложение 1. «Линейные уравнения, методы их решения»

• Приложение 2. «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения»

• Приложение 3. «Дробно-рациональные уравнения, методы их решения»

• Приложение 4. «Уравнения высших порядков, методы их решения»

Для учеников работа над учебными проектами — это возможность максимального раскрытия их творческого потенциала. Она позволяет проявить себя индивидуально или в группе, попробовать свои силы, приложить свои знания, принести пользу, показать публично достигнутый результат. Это деятельность, направленная на решение интересной проблемы, сформулированной зачастую самими учащимися в виде задачи, когда результат этой деятельности — найденный способ решения проблемы — носит практический характер, имеет важное прикладное значение и, что весьма важно, интересен и значим для самих открывателей.

Предварительный просмотр:

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Подписи к слайдам:

Уравнение вида ax + b = 0 где a , b – некоторые числа, x – переменная, называется линейным уравнением.

Если а ≠ 0 , то линейное уравнение имеет единственный корень х = — b/a Если а = 0 ; b ≠ 0 , то линейное уравнение не имеет решений. Если а = 0 ; b = 0 , то х – любое число.

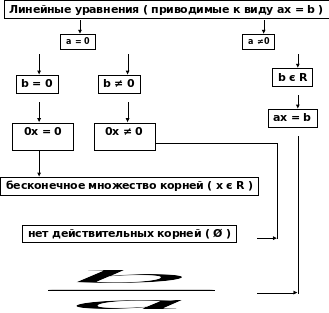
Линейные уравнения (приводимые к виду ax = b ) a = 0 a ≠ 0 b = 0 b ≠ 0 0x = 0 0x ≠ 0 b є R ax = b бесконечное множество корней (x є R) нет действительных корней Один корень ( x = a/b) b = 0 b ≠ 0

Пример 1 . Решим уравнение 2 x – 3 + 4(x – 1) = 5 Решение. 2x – 3 + 4x – 4 = 5 6x = 5 + 4 + 3 6x = 12 x = 12 : 6 x = 2 Ответ : 2

Пример 2. Решим уравнение 2x – 8 – 2(x – 2) = 0 Решение. 2x – 8 – 2x + 4 = 0 — 4 = 0 Ответ : решений нет.

Пример 3. Решим уравнение 3x + 6 – 3(x + 2) = 0 Решение. 3x + 6 – 3x – 6 = 0 0 = 0 Ответ : x – любое число.

Видео:6 способов в одном видеоСкачать

Предварительный просмотр:

Уравнение вида ax + b = 0 , где a , b – некоторые числа x – переменная, называется линейным уравнением.

Алгоритм решения линейного уравнения

Если a ≠ 0, то линейное уравнение имеет единственный корень x = —

Пример: 2x – 3 + 4(x -1) = 5

2x – 3 + 4x – 4 = 5

Если a = 0; b ≠ 0, то линейное уравнение не имеет решений.

Пример: 2x – 8 – 2( x – 2 ) = 0

2x – 8 – 2x + 4 = 0

Ответ: решений нет!

Если a = 0; b =0, то x – любое число.

Пример: 3x + 6 – 3( x + 2 ) = 0

3x + 6 – 3x – 6 = 0

Ответ: x – любое число.

Примеры и решения линейных уравнений.

1. 6х – 12 = 5х + 4 2 . -9а + 8 = -10а – 2

6х – 5х = 12 + 4 -9а + 10а = -8 — 2

х = 16 : 1 а = -10 : 1

Ответ: 16 Ответ: -10

3. 7m + 1 = 8m + 9 4 . 4 + 25y = 6 + 24y

7m – 8m = 9 – 1 25y – 24y = 6 — 4

m = 8 : (-1) y = 2 : 1

Ответ: -8 Ответ: 2

5. 11 – 5z = 12 – 6z 6. 4k + 7 = -3 + 5k

-5z + 6z = 12 – 11 4k – 5k = -3 — 7

z = 1: 1 k = -10 : (-1)

Ответ: 1 Ответ: 10

7. -40 * ( -7x + 5 ) = -1600 8. ( -20x – 50 ) * 2 = 100

280x – 200 = -1600 -40 – 100 = 100

280x = -1600 + 200 -40 = 100 + 100

280x = -1400 40x = 200

x = -1400 : 280 x = 200 : 40

Ответ: -5 Ответ: 5

9. 2.1 * ( 4 – 6y ) = -42 10. -3 * ( 2 – 15x ) = -6

8.4 – 12.6y = -42 -6 + 45x = -6

-12.6 = -42 – 8.4 45x = -6 + 6

-12.6 = -50.4 45x = 0

y = -50.4 : ( -12.6 ) x = 0 : 45

Ответ: 4 Ответ: 0

11. 13 – 5x = 8 – 2x 12. 5x + ( 3x – 7 ) = 9

-5x + 2x = 8 – 13 5x + 3x – 7 = 9

x = -5 : ( -3 ) x = 16 : 8

Ответ: 1, 2/3 Ответ: 2

13. 4y + 15 = 6y + 17 14. 3y – (5 – y) = 11

4y – 6y = 17 – 15 3y – 5 + y = 11

y = 2 : ( -2 ) y = 16 : 4

Ответ: -1 Ответ: 4

15. -27x + 220 = 5x 16. -2x + 16 = 5x — 19

-27x + 5x = — 220 -2x – 5x = -19 — 16

-22x = -220 -7x = -35

x = -220 : ( -22 ) x = -35 : ( -7 )

Ответ: -10 Ответ: 5

17. 25 – 3b = 9 – 5b

18. 3 * (4x – 8 ) = 3x – 6

19. -4 * ( -z + 7) = z + 17

20. c -32 = ( c + 8 ) * ( -7 )

21. 12 – 2 * ( k + 3 ) = 26

22. -5 * ( 3a + 1 ) – 11 = -16

23. -5 * ( 0.8z – 1.2 ) = -z + 7.2

24. -20 * ( x – 13 ) = -220

25. ( 30 – 7x ) * 8 = 352

26. ( 2.8 – 0.1x ) * 3.7 = 7.4

27. ( 3x – 1.2 ) * 7 = 10.5

28. 6x + 12 – 42x = 0

29. 3( y – 5 ) – 2( y – 4 ) = 8

3y – 15 – 2y – 8 = 8

3y – 2y = 8 + 8 + 15

30. -5( 5 – x ) – 4x = 18

Предварительный просмотр:

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Подписи к слайдам:

Определение 1. Квадратным уравнением называют уравнение вида ax 2 + bx + c =0 , где коэффициенты a , b , c — любые действительные числа, причем а≠0. Многочлен ax 2 + bx + c называют квадратным трехчленом.

Определение 2. Корнем квадратного уравнения ax 2 + bx + c =0 называют всякое значение переменной x , при котором квадратный трехчлен ax 2 + bx + c обращается в нуль; такое значение переменной x называют также корнем квадратного трехчлена. Квадратные уравнения с коэффициентами a , b , c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта. Решить квадратное уравнение –значит найти все его корни или установить ,что корней нет.

Определение 3. Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля. Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один коэффициентов b , c равен нулю. Приведенное квадратное уравнение – это квадратное уравнение, в котором а=1.

Определение 4. Для приведенного квадратного уравнения x 2 + px + q =0 сумма корней равна — p , а произведение корней равно q .

Особые квадратные уравнения: 2 x 2 — x -1= 0 D=9 x 1 =1 x 2 =-1 ∕2 2x 2 +3x-5=0 D=49 x 1 =1 x 2 =-5∕2 x 2 +3x-4=0 D=25 x 1 =1 x 2 = -4

3x 2 +2x-1=0 D=16 x 1 = -1 x 2 = 1/3 2x 2 +x-1=0 D=9 x 1 =-1 x 2 =1/2 x 2 -3x-4=0 D=25 x 1 =-1 x 2 =4

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Предварительный просмотр:

Определение 1. Квадратным уравнением называют уравнение вида ax 2 +bx+c=0, где коэффициенты a,b,c- любые действительные числа, причем а≠ 0.

Многочлен ax 2 +bx+c называют квадратным трехчленом.

Определение 2. Корнем квадратного уравнения ax 2 +bx+c=0 называют всякое значение переменной x, при котором квадратный трехчлен ax 2 +bx+c обращается в нуль; такое значение переменной x называют также корнем квадратного трехчлена.

Квадратные уравнения с коэффициентами a, b, c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта.

Решить квадратное уравнение – значит найти все его корни или установить ,что корней нет.

Определение 3. Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля. Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один коэффициентов b,c равен нулю. Приведенное квадратное уравнение – это квадратное уравнение, в котором а=1.

Определение 4. Для приведенного квадратного уравнения x 2 +px+q=0 сумма корней равна

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Проект по математике «Способы решения уравнений различных видов»

Умение учащихся самостоятельно добывать знания и совершенствовать очень важно, потому что современному обществу, производству нужны работники и руководители, способные быстро и правильно решать постоянно возникающие конкретные задачи, вести диалог с коллегами и партнерами, самостоятельно принимать решения. Поэтому на уроках используются технологии, отвечающие современным требованиям. Одной из таких технологий является “технология проектов”. Суть и идея ее заключается в организации самостоятельной, поисковой, творческой деятельности учащихся.

В основу «технологии проектов» положена идея о направленности учебно-познавательной деятельности школьников на результат, который получается при решении той или иной практической или теоретической значимой проблемы. Внешний результат можно увидеть, осмыслить, применить в реальной практической деятельности. Внутренний результат – опыт деятельности – становится достоянием учащегося, соединяя в себе знания и умения, компетенции и ценности.

Просмотр содержимого документа
«Проект по математике «Способы решения уравнений различных видов»»

Проект по математике

«Способы решения уравнений различных видов»

Подготовили учащиеся 8 класса

Учитель математики — Некрасова Тамара Ивановна

«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».

«Посредством уравнений, теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал, и ливни.
Поистине его познанья дивны»

Тема проекта «Способы решения уравнений различных видов»

Тип проекта: групповой, краткосрочный, творческо-исследовательский

Участники проекта: ученики 8 класса.

Сроки реализации проекта: три недели.

Результат: защита проектов, создание презентации, а затем оказание помощи одноклассникам, испытывающим затруднения по данному учебному материалу.

Целью работы является комплектовать все виды уравнений по видам и разобрать основные способы решения данных уравнений.

Задания для групп (в каждой группе 2 человека)

Зачем нужно уметь решать уравнения?

Какими методами решаются уравнения?

1. Обсуждение и утверждение плана работы. Распределение учащихся на группы, выбор каждой группой вопросов-заданий и форм (проектных продуктов) представления результатов работы (первая неделя).

2. Изучение и анализ источников и литературы.(вторая неделя)

3. Оформление результатов работы над проектом.(вторая неделя)

4. Представление проектных продуктов.(третья неделя)

Работа над проектом

Подбор исторических сведений об уравнениях (1 учащийся)

Задание для группы 1.

Собрать информацию по теме «Линейные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).

Подобрать 10 – 15 уравнений по данной теме (вместе с решением).

Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).

Подготовиться к защите проекта.

Задание для группы 2.

Собрать информации по теме «Квадратные уравнения и уравнения, приводимые к квадратным, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).

Подобрать 10 – 15 уравнений по данной теме (вместе с решением).

Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).

Подготовиться к защите проекта.

Задание для группы 3.

Собрать информации по теме «Дробно-рациональные уравнения, методы их решения» (источники: материалы учебников алгебры 7-8, справочники, Интернет).

Подобрать10 – 15 уравнений по данной теме (вместе с решением).

Оформить отчёт о проделанной работе: теория + практические задания («бумажный» вариант).

Подготовиться к защите проекта.

Создание презентации (коллективная работа)

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было нимонет, ни кошельков. Но зато были кучи, а также горшки, корзины, которыепрекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37. «, — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число

павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.

Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика»

греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

1) Сейчас мы с вами рассмотрим решения линейных уравнений.

Вспомним, что уравнение вида ax+b=0 называется линейным уравнением или

уравнением первой степени так как при переменной «х» старшая степень

находится в первой степени.

Решение линейного уравнения очень простое:

Пример 1 Решите уравнение 3x+3=5x

Линейное уравнение решается методом переноса членов содержащих

неизвестные в левую часть от знака равенства, свободные коэффициенты в

правую часть от знака равенства:

Значение переменной, обращающее уравнение в верное равенство

называется корнем уравнения.

Выполнив проверку получим:

Значит 1,5 – корень уравнения.

Решения уравнений методом переноса слагаемых из одной части

уравнения в другую, при этом знак слагаемых меняется на противоположный

и применяют свойства уравнений – обе части уравнения можно умножить

(разделить) на одно и то же отличное от нуля число или выражение, можно

рассмотреть при решении следующих уравнений.

Пример 2 Решите уравнения:

а) 6x+1=− 4x; б) 8+7x=9x+4; в) 4(x−8)=− 5

а) Методом переноса решаем

б) Аналогично предыдущему примеру решаем методом переноса:

в) В данном уравнении необходимо раскрыть скобки, применяя

распределительное свойство умножения относительно операции сложения.

📺 Видео

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение системы уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Линейное уравнение с одной переменной. 6 класс.Скачать

МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Решение системы линейных уравнений. Подстановка. С дробными выражениями.Скачать