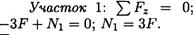Продольные силы определяются из уравнения

Видео:построение эпюры продольных силСкачать

Продольная сила — внутренний силовой фактор

Приветствую тебя, читатель портала о сопромате и не только – SoproMats. В сегодняшней статье поговорим о таком важном внутреннем силовом факторе как продольная сила. Расскажем, что это за сила, зачем нужна и все в таком духе. Обещаем максимально подробно раскрыть данную тему, а также дать ссылки на смежные статьи, которые касаются продольной силы. Например, укажем ссылку, где можно почитать о построении эпюры распределения продольных сил и т.д.

Видео:определение реакций в стержнях от действия грузовСкачать

Что такое продольная сила?

Продольная сила – это внутренний силовой фактор, который возникает в поперечных сечениях элементов, работающих на центральное растяжение (сжатие). Конечно, продольная сила может возникать не только в элементах, которые работают только на растяжение и сжатие. Она может возникать в сечениях, как ОДИН ИЗ силовых факторов, совместно с поперечной силой или изгибающим моментом. Но это все возможно при сложных видах сопротивления конструкций. В данном уроке мы будем говорить только о чистом растяжении или сжатии.

Зачем нужна?

Этот силовой фактор используется в расчетах на прочность и жесткость элементов конструкций, работающих на растяжение (сжатие). Зная продольную силу можно определить нормальные напряжения в поперечных сечениях элементов, после чего подобрать их размеры, которые бы удовлетворяли условию безопасной прочности, либо проверить прочность, если размеры элемента изначально заданы. Также можно определить осевые перемещения поперечных сечений, после чего сделать вывод о жесткости детали.

Как определяется?

Как и другие внутренние силовые факторы, продольная сила определяется методом сечений. Для того чтобы определить продольную силу в произвольном сечении элемента, его мысленно рассекают в этом сечении на две части, рассматриваются равновесие одной из частей, заменив действие отброшенной части продольной силой. Из уравнения статики, в частности, суммы проекций на одну из осей, выражается продольное усилие. Для построения эпюр, эту процедуру проводят несколько раз, для каждого участка стержня (бруса). Более детально этот процесс рассмотрим ниже, когда будем изучать подробный способ построения эпюры.

Как обозначается?

Продольная сила обозначается буквой N с индексом, который совпадает с названием продольной оси, направленной в сторону растяжения или сжатия нагруженного элемента и перпендикулярной поперечным сечениям. Чаще всего, эта ось обозначается буквой – x. Потому в нашем уроке будем использовать обозначение продольной силы — N_x.

В чем измеряется?

Продольная сила, как и обычные внешние сосредоточенные силы, измеряется в ньютонах. На практике, в расчетах используются килоньютоны (кН). Также иногда в литературе можно встретить размерность – кгс и тс.

Видео:Математика это не ИсламСкачать

Полезные статьи о продольной силе

Здесь буду публиковать ссылки на полезные статьи, которые тесно связанны с продольной силой.

Построение эпюры

В этой статье, про построение эпюр продольных сил, Вы узнаете, как рассчитывается эпюра продольных сил на примере ступенчатого бруса, на который действуют различные виды нагрузок. Кроме того, в ней рассмотрено три методики расчета, что позволит всесторонне разобраться в этом вопросе.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Продольная сила. Метод сечений. Эпюры продольных сил

Видео:канонические уравнения метода силСкачать

Внутренние силы при растяжении-сжатии

Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие ( продольная сила $N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.

Продольная сила при растяжении считается положительной, при сжатии – отрицательной .

Пример определения внутренних сил.

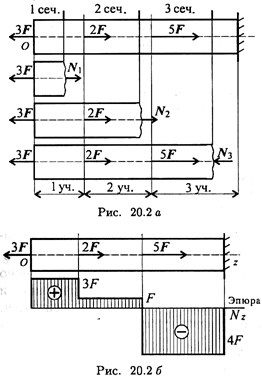
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.

Участком нагружения считают часть бруса между внешними силами.

На представленном рисунке 3 участка нагружения.

Воспользуемся методом сечений и определим внут­ренние силовые факторы внутри каждого участка.

Расчет начинаем со свободного конца бруса, что­бы не определять величины реакций в опорах.

Продольная сила положи­тельна, участок 1 растянут.

Продольная сила положительна, участок 2 растянут.

Продольная сила отрицательна, участок 3 сжат.

Полученное значение N₃ равно реакции в заделке.

Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси.

Нулевая линия про­водится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.

В пределах одного участка значение силы не меняется, поэто­му эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

Напряжения. Действующие и допускаемые напряжения

Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.

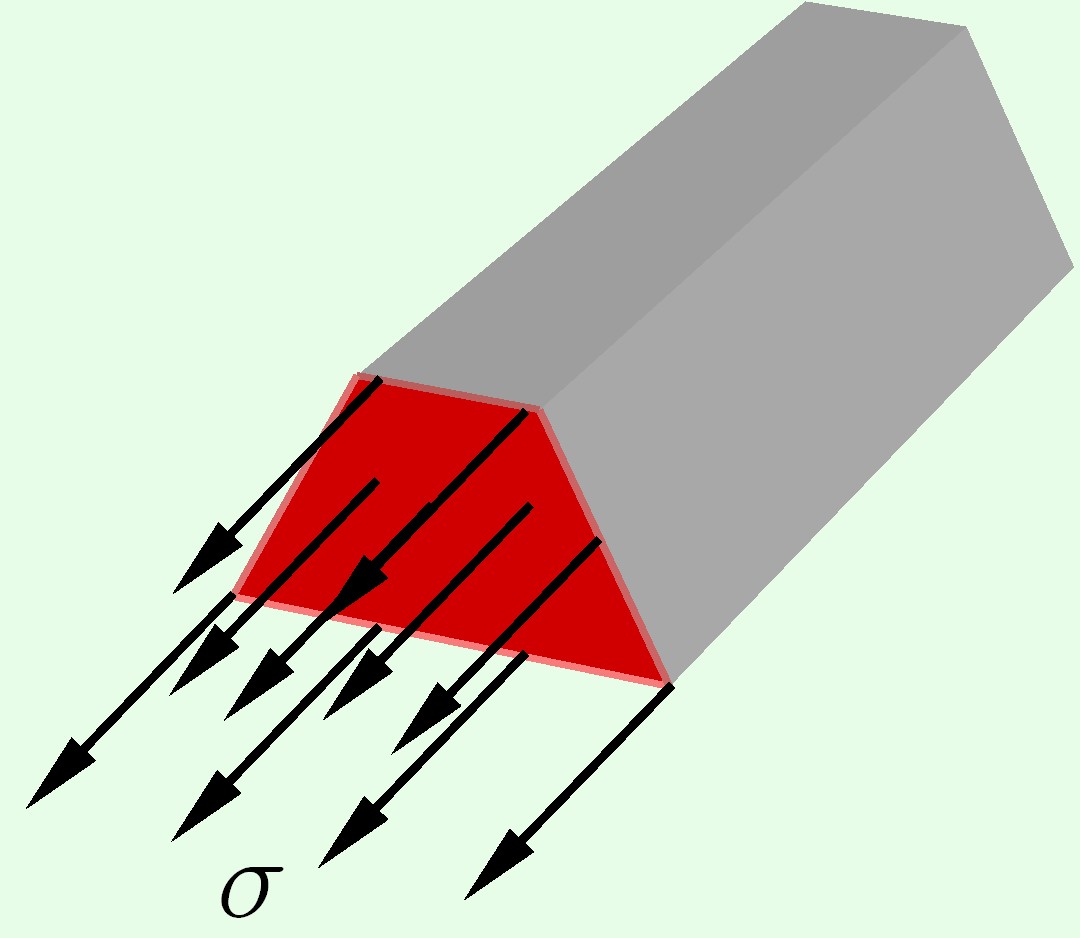
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными .

Видео:Канонические уравнения метода силСкачать

$sigma = frac$

Единицы измерения напряжений — Па, кПа, МПа.

Знаки напряжений принимают так, как и для продольной силы.

Действующие напряжения — напряжения, которые возникают в рассматриваемом сечении.

Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.

Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.

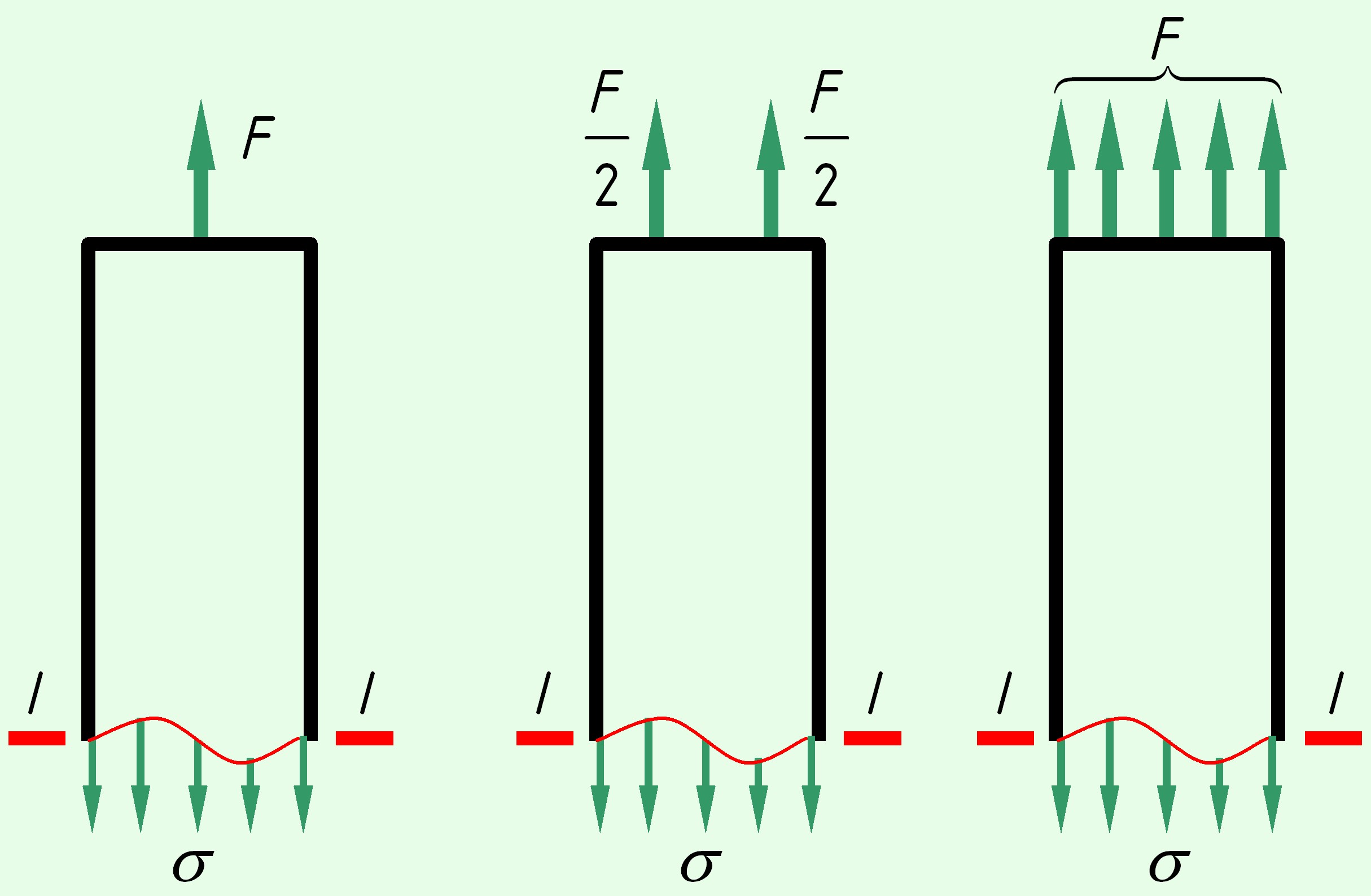
Принцип Сен-Венана : в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.

то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.

Рисунок — иллюстрация принципа Сен-Венана

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Абсолютная и относительная деформация

При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией .

Относительная деформация – отношение абсолютной деформации к первоначальной длине.

$sigma = E cdot varepsilon $

Таблица — физико-механические характеристики материалов

Видео:РАСТЯЖЕНИЕ-СЖАТИЕ. Построение эпюр. Сопромат.Скачать

Как определить продольную силу?

Автор: Константин Вавилов · Опубликовано 22.07.2015 · Обновлено 04.12.2017

Решение практически любой задачи на растяжение (сжатие) начинается с определения продольных сил. Зная их величину можно определить такие важные параметры как напряжение или перемещение. Как говорилось ранее, при чистом растяжении (сжатии) возникает лишь один внутренний силовой фактор – нормальная сила N. Также ее иногда обзывают продольной силой. Для разнообразия я буду писать и так.

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Как определить?

Как же определить эту самую силу? Для этого воспользуемся методом сечений. Мысленно рассечем тело, нагруженное растягивающей силой F, в произвольном месте. Отбросим одну из частей бруса и заменим действие отброшенной части нормальной силой N. Если спроецировать все силы на ось z и записать условие равновесия то получим:

То есть продольная сила N численно равна внешней силе F. Причем не трудно догадаться, что значение силы N будет постоянно по всей длине бруса.

Для наглядности построим эпюру продольных сил. Причем при построении необходимо учитывать правило знаков.

Если силы растягивающие, то условно считаем их положительными. Если сжимающие, то считаем их отрицательными.

В нашем случае сила F стремится растянуть брус, эпюру откладываем сверху со знаком «+».

📹 Видео

Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать

Осевое растяжение (сжатие). Построение эпюры продольных сил.Скачать

Построение эпюр в балке ( Q и M ). СопроматСкачать

Определение усилий, напряжений и перемещений. СопроматСкачать

Урок 10. Сложные уравнения и неравенства. Решение уравнений высоких степеней. Вебинар | МатематикаСкачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Урок 347. Вынужденные колебания. Резонанс (часть 1)Скачать

Коэффициенты и свободные члены канонических уравнений метода силСкачать

Пример определения продольной силы и нормального напряжениеСкачать